1. Stack

Stack, a place for storing goods or accommodating passengers, can be extended to warehouse and transfer station. Therefore, when introduced into the field of computer, it refers to the place where data is temporarily stored. Therefore, there is the saying of entering and leaving the stack. It can be compared to eating, and spitting out after eating is a stack

1.1 concept of stack

Stack, also known as stack, is a linear table with limited operation. Limit linear tables to insert and delete only at the end of the table. This end is called the top of the stack, and the other end is called the bottom of the stack. Inserting a new element into a stack is also called stack entry, stack entry or stack pressing. It puts the new element above the top element of the stack to make it a new top element; Deleting an element from a stack is also called out of stack or out of stack. It deletes the top element of the stack and makes its adjacent elements become new top elements.
Stack features: last in first out

Note: the stack cannot be traversed

1.2 implementation method of stack

The implementation of stack can generally be realized by array or linked list. Relatively speaking, the structure implementation of array is better. Because the array inserts data at the end
The cost is relatively small.

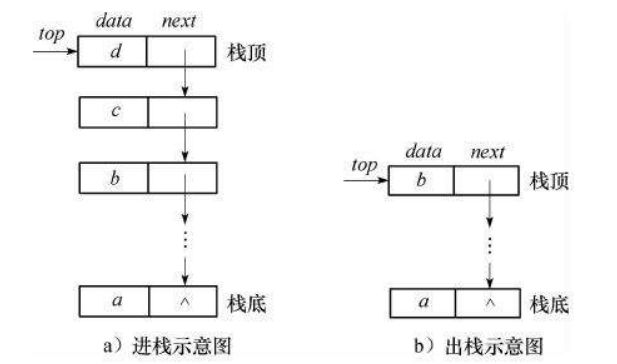
1.3 simulation implementation of stack -- dynamic memory

Stack.h

#pragma once

typedef int DataType;

typedef struct Stcak
{
	DataType *arr;
	int capacity;	//Capacity size
	int size;	//Number of effective elements --- stack top
}Stack; 

//Initialization of stack
void StackInit(Stack *ps);

//Push 
void StackPush(Stack *ps, DataType data);

//Out of stack
void StackPop(Stack *ps);

//Get stack top element
DataType StackTop(Stack *ps);

//Gets the size of the stack
int StackSize(Stack *ps);

//Determine whether there are elements in the stack
int StackEmpty(Stack *ps);

//Destroy stack
void StackDestroy(Stack *ps);

void TestStack();

Stack.c

#include"Stack.h"
#include<stdio.h>
#include<assert.h>
#include<malloc.h>

//Initialization of stack
void StackInit(Stack *ps)
{
	assert(ps);
	ps->arr = (DataType *)malloc(sizeof(DataType)* 3);
	if (NULL == ps->arr)	//Check whether the space application is successful
	{
		assert(0);
		return;
	}
	ps->capacity = 3;;
	ps->size = 0;
}

//Check capacity
void CheckCapacity(Stack *ps)
{
	if (ps->size == ps->capacity)
	{
		ps->arr = (DataType*)realloc(ps->arr, sizeof(DataType)*ps->capacity * 2);
		if (NULL == ps->arr)	//Check whether the space application is successful
		{
			assert(0);
			return;
		}
		ps->capacity *= 2;
	}
}


//Push 
void StackPush(Stack *ps, DataType data)
{
	assert(ps);
	CheckCapacity(ps);	//Capacity expansion
	ps->arr[ps->size++] = data;
	
}

//Out of stack
void StackPop(Stack *ps)
{
	assert(ps);
	if (StackEmpty(ps))	//Check whether the stack is empty at this time
		return;
	ps->size--;
}

//Get stack top element
DataType StackTop(Stack *ps)
{
	assert(ps && !StackEmpty(ps));
	//If condition judgment cannot be used here, because if condition judgment is legal
	//If the stack is empty and there are no elements in the stack, it is illegal to obtain the top element of the stack
	//You can use assert to judge
	//if (StackEmpty(ps))
	//	return;
	return ps->arr[ps->size - 1];
}

//Gets the size of the stack
int StackSize(Stack *ps)
{
	assert(ps);
	return ps->size;
}

//Determine whether there are elements in the stack
int StackEmpty(Stack *ps)
{
	assert(ps);
	return 0 == ps->size;
}

//Destroy stack
void StackDestroy(Stack *ps)
{
	assert(ps);
	if (ps->arr)
	{
		free(ps->arr);
		ps->arr = NULL;
		ps->capacity = 0;
		ps->size = 0;
	}
}

void TestStack()
{
	Stack con;
	StackInit(&con);

	StackPush(&con, 1);
	StackPush(&con, 2);
	StackPush(&con, 3);
	StackPush(&con, 4);
	StackPush(&con, 5);
	StackPush(&con, 6);
	printf("size = %d\n", StackSize(&con));
	printf("top = %d\n", StackTop(&con));

	StackPop(&con);
	StackPop(&con);
	StackPop(&con);
	printf("size = %d\n", StackSize(&con));
	printf("top = %d\n", StackTop(&con));

	StackDestroy(&con);
}

test.c

#define _CRT_SECURE_NO_WARNINGS

#include"Stack.h"

int main()
{
	TestStack();
	return 0;
}

1.4 OJ questions about stack

1. Bracket matching problem OJ

1.5 inverse Polish expression

1.5.1 concept

Inverse Polish expression is also called suffix expression. Inverse Polish expression is an expression method first proposed by Polish logician J. Lukasiewicz in 1929 [1]. Later, the expression written with this representation was called "inverse Polish expression". The inverse Polish expression writes the amount of computation in the front and the operator in the back.

1.5.2 stack implementation inverse Polish expression

Its advantage is that it can handle the operation of any ordinary expression with only two simple operations, input and output. The calculation method is as follows:
If the current character is a variable or a number, it will be pressed on the stack. If it is an operator, the two elements at the top of the stack will be popped up for corresponding operation, and the result will be put on the stack. Finally, when the expression is scanned, the result in the stack will be the result.

2. Queue

Equivalent to eating in and pulling out.

2.1 concept of queue

Queue is a special linear table, which only allows deletion at the front of the table and insertion at the back of the table. The end of the insertion operation is called the end of the queue, and the end of the deletion operation is called the head of the queue.
Queue characteristics: first in first out.

2.2 implementation method of queue

The queue can also be implemented in the structure of array and linked list. It is better to use the structure of linked list, because if the structure of array is used, the efficiency will be relatively low.

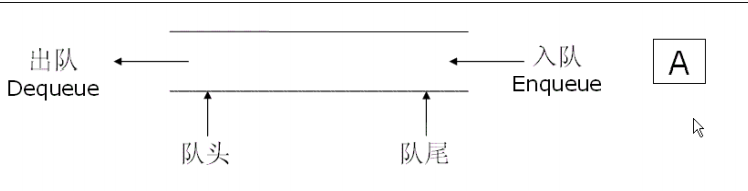
2.3 simulation implementation of queue -- chain

Queue.h

#pragma once

typedef int QDataType;
typedef struct QListNode
{
	struct QListNode* next;
	QDataType data;
}QNode;

// Queue structure
typedef struct Queue
{
	QNode* front;
	QNode* rear;
}Queue;

// Initialize queue
void QueueInit(Queue* q);
// Tail in queue
void QueuePush(Queue* q, QDataType data);
// Queue leader out of queue
void QueuePop(Queue* q);
// Get queue header element
QDataType QueueFront(Queue* q);
// Get queue tail element
QDataType QueueBack(Queue* q);
// Gets the number of valid elements in the queue
int QueueSize(Queue* q);
// Check whether the queue is empty. If it is empty, a non-zero result will be returned. If it is not empty, 0 will be returned 
int QueueEmpty(Queue* q);
// Destroy queue
void QueueDestroy(Queue* q);

Queue.c

#include"Queue.h"
#include<assert.h>
#include<stdio.h>
#include<malloc.h>

QNode* BuyQueueNode(QDataType data)
{
	QNode* node = (QNode *)malloc(sizeof(QNode));
	if (NULL == node)
	{
		assert(0);
		return NULL;
	}
	node->data = data;
	node->next = NULL;
	return node;
}

// Initialize queue
void QueueInit(Queue* q)
{
	assert(q);
	q->front = q->rear = BuyQueueNode(0);
}

// Tail in queue
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	q->rear->next = BuyQueueNode(data);
	q->rear = q->rear->next;
}
// Queue leader out of queue
void QueuePop(Queue* q)
{
	QNode *delNode = NULL;
	if (QueueEmpty(q))
		return;
	delNode = q->front->next;
	q->front->next = delNode->next;

	//If there is only one element in the queue at this time, you need to put the rear in the front position after deleting the element
	if (delNode->next == NULL)
		q->rear = q->front;
	free(delNode);
}

// Get queue header element
QDataType QueueFront(Queue* q)
{
	assert(!QueueEmpty(q));
	return q->front->next->data;
}

// Get queue tail element
QDataType QueueBack(Queue* q)
{
	assert(!QueueEmpty(q));
	return q->rear->data;
}

// Gets the number of valid elements in the queue
int QueueSize(Queue* q)
{
	assert(q);
	int count = 0;
	QNode* cur = q->front->next;
	while (cur)
	{
		cur = cur->next;
		count++;
	}
	return count;
}

// Check whether the queue is empty. If it is empty, a non-zero result will be returned. If it is not empty, 0 will be returned 
int QueueEmpty(Queue* q)
{
	assert(q);
	return q->front->next == NULL;
}

// Destroy queue
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* cur = q->front;
	while (cur)
	{
		q->front = cur->next;
		free(cur);
		cur = q->front;
	}
	q->front = q->rear = NULL;
}

//test
void TestQueue()
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, 1);
	QueuePush(&q, 2);
	QueuePush(&q, 3);
	QueuePush(&q, 4);
	QueuePush(&q, 5);
	QueuePush(&q, 6);
	printf("size = %d\n", QueueSize(&q));
	printf("front = %d\n", QueueFront(&q));
	printf("rear = %d\n", QueueBack(&q));

	QueuePop(&q); 
	QueuePop(&q);
	QueuePop(&q);
	printf("size = %d\n", QueueSize(&q));
	printf("front = %d\n", QueueFront(&q));
	printf("rear = %d\n", QueueBack(&q));

	QueuePop(&q);
	QueuePop(&q);
	printf("size = %d\n", QueueSize(&q));
	printf("front = %d\n", QueueFront(&q));
	printf("rear = %d\n", QueueBack(&q));


	QueuePop(&q);
	printf("size = %d\n", QueueSize(&q));

	if (QueueEmpty(&q))
	{
		printf("Empty\n");
	}
	else
	{
		printf("Error\n");
	}

	QueueDestroy(&q);
}

test.c

#include"Queue.h"

int main()
{
	TestQueue();
	system("pause");
	return 0;
}

2.4 array implementation of queue - sequential mode

The queue can be stored in the array Q[1... M], and the upper bound m of the array is the maximum capacity allowed by the queue. In the operation of queue, two pointers need to be set: head, queue head pointer, pointing to the actual queue head element; Tail, tail pointer, pointing to the next position of the actual tail element. Generally, the initial value of the two pointers is set to 0. At this time, the queue is empty and there are no elements. Array definition Q[1... 10]. Q(i) i=3,4,5,6,7,8. The head pointer is head=2 and the tail pointer is tail=8. The number of elements in the queue is: l = tail head. Now, to get the top elements out of the queue, you need to add 1 to the head pointer. That is, head=head+1. At this time, the head pointer moves up one position and points to Q(3), indicating that Q(3) has been out of the queue. If you want a new element to join the queue, you need to move the tail pointer up one position. That is, tail=tail+1, and then Q(9) joins the team. When the end of the queue has been processed at the top, that is, tail=10, if the queue entry operation needs to be performed, an "overflow" will occur, but there are actually three empty positions in the queue, so this overflow is called "false overflow".

There are two ways to overcome false overflow. One is to move all elements in the queue to the low address area, which is obviously a waste of time; Another method is to treat the array storage area as a ring area connected end to end. When it is stored in the n address, the next address will be "flipped" to 1. The queue that uses this technique to store in structure is called circular queue.

Circular queue is introduced to solve false overflow

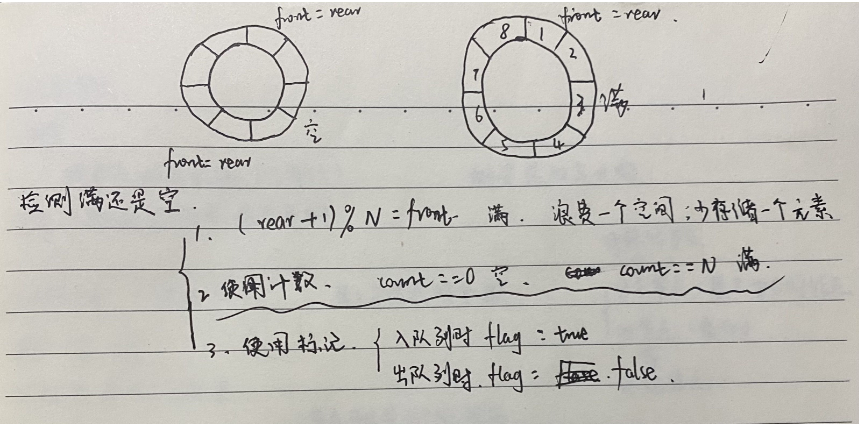
2.5 queue OJ questions

1. Implement stack OJ with queue simulation
2. Implement queue OJ with stack simulation
3. Design cycle queue OJ

Summary and perception

I'll only write so many knowledge points and interview questions about stacks and queues here. If I think of other things in the future, I'll slowly add them. That's what I realized in the early stage. If you have different views or have different ideas, you are welcome to honor me. Based on the principle of mutual progress, I hope you can give me more opinions. Thank you~~

The stack and queue are basically over. The next chapter - tree preview, Lala~