1. Three basic sorts
1.1 bubble sorting
#include <iostream>
using namespace std;
int main()
{
int arr[]={2,1,4,21,4,24,9,18};
int len = sizeof(arr)/sizeof(arr[0]);
for(int i = 0;i < len; ++i)
{
for(int j = i+1;j<len;++j)
{
if(arr[i]<arr[j])
{
arr[i]= arr[i]^arr[j];
arr[j]= arr[i]^arr[j];
arr[i]= arr[i]^arr[j];
}
}
}
for(int i =0;i<len;++i)
cout<<arr[i]<<endl;
}1.2 selection and sorting
#include <iostream>
using namespace std;
int main(void)
{
int arr[] = { 2, 1, 4, 21, 4, 24, 9, 18 };
int len = sizeof(arr) / sizeof(arr[0]);
int minindex;
for (int i = len - 1; i > 0; --i)
{
minindex = 0;
for (int j = i; j >0; --j)
{
if (arr[j] < arr[minindex])
{
minindex = j;
}
}
if (minindex != i)
{
arr[minindex] = arr[i] ^ arr[minindex];
arr[i] = arr[i] ^ arr[minindex];
arr[minindex] = arr[i] ^ arr[minindex];
}
}
for (int i = 0; i < len; ++i)
cout << arr[i] << endl;
}1.3 insert sort
int main(void)
{
int arr[] = { 2, 1, 4, 21, 4, 24, 9, 18 };
int len = sizeof(arr) / sizeof(arr[0]);
for (int i = 1; i < len; ++i)
{
for (int j = i - 1; j >= 0; --j)
{
if (arr[j]<arr[j + 1])
{
arr[j + 1] = arr[j] ^ arr[j + 1];
arr[j] = arr[j] ^ arr[j + 1];
arr[j + 1] = arr[j] ^ arr[j + 1];
}
else break;
}
}
for (int i = 0; i < len; ++i)
cout << arr[i] << endl;
}2. Hill sort
Hill sort optimizes the insertion sort in the following way: use the bisection method to insert each data of the latter part into the former part in a similar way. The sorting is completed until it can no longer be divided, as shown in the following figure:
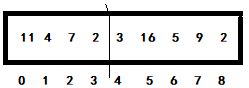
<1> Divide the array into two by one, and the comparison step is half the length of the array. As shown in the figure above, insert the latter part into the former part, and the two pointers in the figure below point to the first part and the second part respectively

When the green pointer subscript is 4, it is compared with the red pointer subscript of 0. If the conditions are met, it will be exchanged, and the red pointer will be moved back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, if 11 > 3, exchange. Then move the green and red subscripts back. As shown below:
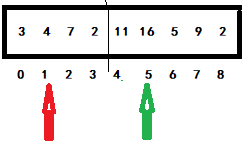
When the green pointer subscript is 5, it is compared with the red pointer subscript is 1. If the conditions are met, it is exchanged, and the red pointer is moved back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, if 4 < 16, go directly to the next judgment. Move the green and red subscripts back. As shown below:
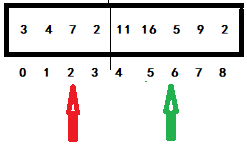
When the green pointer subscript is 6, compare it with the red pointer subscript is 2. If the conditions are met, exchange and move the red pointer back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, if 7 > 5, it will be switched. The green will not move, and the red will move back one bit, as shown in the following figure:
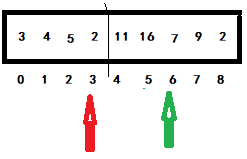
When the green pointer subscript is 6, it is compared with the red pointer subscript is 3. If the conditions are met, it is exchanged, and the red pointer is moved back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, 2 < 7 directly enters the next judgment. As shown below:
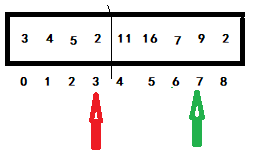
When the green pointer subscript is 7, compare it with the red pointer subscript is 3. If the conditions are met, exchange and move the red pointer back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, 2 < 7 directly enters the next judgment. As shown below:
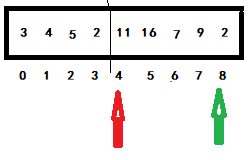
When the green pointer subscript is 8, it is compared with the red pointer subscript is 4. If the conditions are met, it is exchanged, and the red pointer is moved back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, if 11 > 2, it will be switched. The green will not move, and the red will move back one bit, as shown in the following figure:
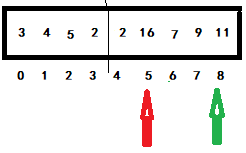
When the green pointer subscript is 8, it is compared with the red pointer subscript of 5. If the conditions are met, it will be exchanged, and the red pointer will be moved back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, if 16 > 11, it will be switched. The green will not move, and the red will move back one bit, as shown in the following figure:
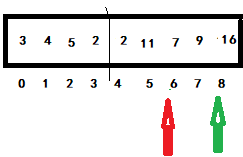
When the green pointer subscript is 8, compare it with the red pointer subscript is 6. If the conditions are met, exchange and move the red pointer back one bit. Otherwise, directly move the green pointer back one bit to enter the next judgment. Obviously, 2 < 7 directly enters the next judgment. At this time, the green subscript will cross the boundary and enter the next two points.
<2> Change the comparison length to the general of < 1 >, and so on. Get:
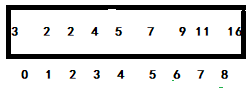
<3> Change the comparison length to half of < 2 >, and so on. Get:
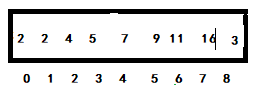
At this time, the exchange step is 0 after two points, and the sorting is completed.
The implementation algorithm is as follows:
#include<iostream>
using namespace std;
int main(void)
{
int arr[] = { 11,4,7,2,3,16,5,9,2 };
int len = sizeof(arr) / sizeof(arr[0]);
int step= len >> 1;//Step represents the comparison step
while (step)
{
for (int i = step; i<len; ++i)
{
for (int j = i - step; j >= 0; j -= step)
{
if (arr[j]>arr[j + step])
{
arr[j] = arr[j] ^ arr[j + step];
arr[j + step] = arr[j] ^ arr[j + step];
arr[j] = arr[j] ^ arr[j + step];
}
else break;
}
}
step= step>> 1;
}
for (int i = 0; i < len; ++i)
cout << arr[i] << endl;
}3. Merge and sort
Idea of merging and sorting: using the methods of recursion and bisection, first divide the array into left and right parts according to the subscript, then recursively sort the left and right parts, and finally sort the separated two parts. When the array subscript is no longer separable, the recursion ends.
The merging algorithm for sorting the two parts of the array after separation is as follows:
Because the array is divided into two parts according to the subscript, which are separated by mid=(L+R)/2, and these two parts are the two parts that have been sorted by recursion, we use three pointers, l and R, to point to the heads of the left and right parts respectively. As shown in the figure:
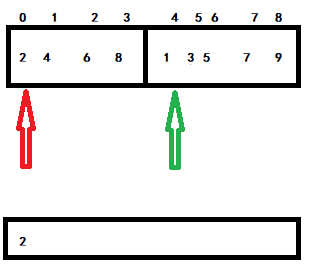
Then prepare an extra space to hold the ordered data. Compare the data pointed to by the two pointers, put the smaller one in help, and move the smaller pointer back at the same time. If a pointer is moved to the last but another pointer is not moved to the last, the remaining data of the pointer that is not moved to the last will be put into help in turn. Finally, update the original array with help array.
As shown below:
Step 1, 2 > 1, green backward:
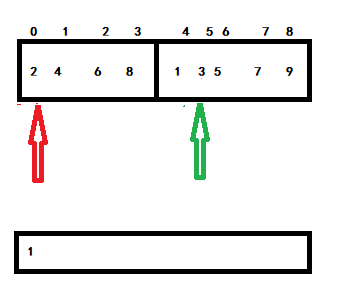
Then 2 < 3, the red moves back
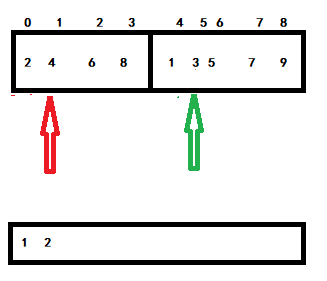
And so on until a pointer is out of bounds, then put the remaining data of another pointer into help, and finally put arr=help.
Program implementation
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<vector>
using namespace std;
void mergeSort(vector<int>&arr);
void mergeSort(vector<int>&arr, int l, int r);
void merge(vector<int>&arr, int l, int mid, int r);
void mergeSort(vector<int>&arr)//The main algorithm uses vector to store data
{
if (arr.size() < 2)
{
return;
}
mergeSort(arr, 0, arr.size()-1);//Enter sort
}
void mergeSort(vector<int>&arr,int l,int r)
{
if (l == r)return;//When the left and right subscripts coincide, it indicates that they can no longer be separated
int mid = (l + r) / 2;//Split the current array into two
mergeSort(arr, l, mid);//Sort left part
mergeSort(arr, mid + 1, r);//Sort right part
merge(arr, l, mid, r);//Use the merge algorithm to complete the merge
}
void merge(vector<int>&arr, int l, int mid, int r)
{
int len = r - l + 1;
int *help = new int[len];//Open up additional space
int i = 0;
int p1 = l;
int p2 = mid + 1;
while (p1<=mid&&p2<=r)
{
help[i++] = arr[p1] > arr[p2] ? arr[p1++] : arr[p2++];//Which little pointer puts that in help and then adds the little pointer + 1
}
//Next, put the remaining data into help
while (p1<=mid)
{
help[i++] = arr[p1++];
}
while (p2 <= r)
{
help[i++] = arr[p2++];
}
//Update arr
for (int i = 0; i < len; ++i)
{
arr[i + l] = help[i];
}
delete[]help;//Release help
}
int main03(void)
{
vector<int>arr;
arr.push_back(1);
arr.push_back(3);
arr.push_back(2);
arr.push_back(45);
arr.push_back(5);
mergeSort(arr);
for (int i = 0; i < arr.size(); ++i)
{
cout << arr[i] << endl;
}
system("pause");
return 0;
}4. Quick sort
Before we know about quick sorting, we first know a problem, which is the "Dutch flag problem":
Dutch flag issue
Given an array arr and a number num, put the number less than num on the left of the array, the number equal to num in the middle of the array, and the number greater than num on the right of the array. The required time complexity is O(N), and the additional space complexity is O(1)
Solution: given an array, use the less pointer and the more pointer to point to both ends of the array respectively. (less more just crossed the boundary) as shown in the figure:
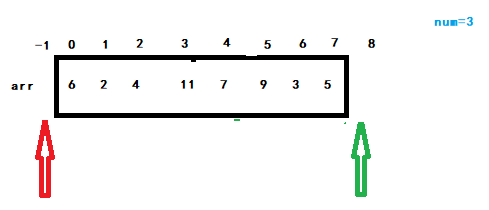
Next, prepare another pointer cur, starting with a subscript of 0.
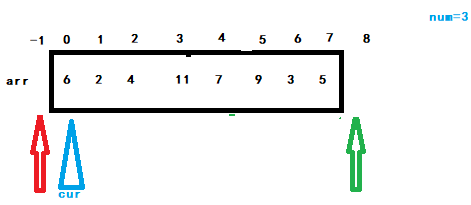
Then compare the sizes of arr[0] and num. if they are equal, directly add cur+1. If they are less than, add red pointer + 1, and exchange the number corresponding to the red pointer after + 1 with arr[cur]. Then cur+1. If they are greater than num, add green pointer - 1, exchange the data corresponding to the green pointer after - 1 with arr[cur], and then make arr[cur] re um compare. When cur coincides with the green pointer, the arrangement is completed.
Program algorithm
int main(void)
{
int arr[] = { 11,3,7,2,3,16,5,9,2 };
int len = sizeof(arr) / sizeof(arr[0]);
int num = 3;
int L = -1;//less
int M = len;//more
int cur = 0;//cur
while (cur!=M)//When cur==M, the arrangement is completed
{
if (arr[cur] < num)
{
//If less than
L++;
arr[L] = arr[L] ^ arr[cur];
arr[cur] = arr[L] ^ arr[cur];
arr[L] = arr[L] ^ arr[cur];
cur++;
}
else if (arr[cur] > num)
{
//If greater than
M--;
arr[M] = arr[M] ^ arr[cur];
arr[cur] = arr[M] ^ arr[cur];
arr[M] = arr[M] ^ arr[cur];
}
else
{
cur++;
}
}
for (int i = 0; i < len; ++i)
cout << arr[i] << endl;
}Quick sorting is to use the solution idea of the Dutch flag problem and recursively. Each sub process takes the last number of the array of sub processes as the num of the Dutch flag problem. As shown in the figure: suppose the last number of the main process is x
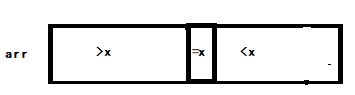
The subprocess recurses the two parts of > x and < x, and places the last number greater than the subprocess on the left and less than the subprocess on the right. As shown in the figure, it is assumed that the last number in the > x part is x1 and the last number in the < x part is x2

Recursion in turn until it can no longer be divided.
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include <time.h>
using namespace std;
//The improved quick sort is divided into random quick sort and random quick sort
void quick(int arr[],int l,int r)
{
if (l < r)
{
//Add the following lines of code to program random fast scheduling:
int t = arr[r];
int rand_pos = rand() % (r-l+1) + l;
arr[r] = arr[rand_pos];
arr[rand_pos] = t;
//Is to randomly choose a number in l-r and exchange it with the tail
int c = l;
int less = l - 1;
int more = r;
while (c < more)
{
if (arr[c] < arr[r])
{
less++;
int temp = arr[less];
arr[less] = arr[c];
arr[c] = temp;
c++;
}
else if (arr[c]>arr[r])
{
more--;
int temp = arr[more];
arr[more] = arr[c];
arr[c] = temp;
}
else
{
c++;
}
}//The above is the number from 0 to r-1 according to the Dutch flag
int temp = arr[more];
arr[more] = arr[r];
arr[r] = temp;//Exchange the r-th element with the element at more to completely change it into a qualified array
quick(arr, l, less);
quick(arr, more+1, r);//Recursion is used to deal with these two parts
}
}
int main04(void)
{
srand(time(NULL));
int a[] = { 3, 4, 2, 5, 1, 7, 6, 88, 2 };
int len = sizeof(a) / 4;
quick(a, 0, len - 1);
for (int i = 0; i < len; ++i)
{
cout << a[i] << endl;
}
system("pause");
return 0;
}5. Heap sorting
Heap structure is actually a complete binary tree structure. A full binary tree must be a complete binary tree. As long as the tree structure is satisfied, the nodes from left to right are supplemented in turn. Such a tree structure is also called a complete binary tree.
If an array is used to simulate a complete binary tree, subscripts can be used. The left child of the ith node is 2xi+1, the right child of the ith node is 2xi+2, and the parent node of the ith node is (i-1)/2
Large root heap: the maximum value of the whole tree is the root node, and the head of any subtree is the maximum value of the subtree of the tree. (c + + the bottom layer of the priority queue is the large root heap 0
Small root heap: the minimum value of the whole tree is the root node, and the head of any subtree is the minimum value of the subtree of the tree.
5.1 how to build a heap -- take the large root heap as an example:
Node insertion
For a set of data: int arr[] = {2,1,3,6,0,4}; It is assumed that the internal data of the array has been arranged according to the complete binary tree.
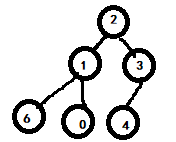
Then we access the array elements in turn. Because there is no parent node when arr[0]=2, it is the root node, so we build a large root heap from where arr[1]=1. The process is as follows:
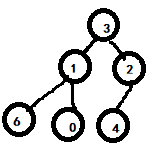
First, access arr[1] and find its parent node arr[(1-1)/2]=2 through subscript. Since 2 > 1, it will not be processed. Then access the next node arr[2]=3 and find its parent node arr[(2-1)/2]=2 through the subscript. Because 2 < 3, exchange these two values. The tree structure changes to:
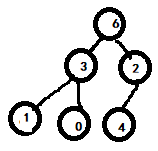
Then access arr[3]=6 and find its parent node arr[(3-1)/2]=1 through subscript. Because 1 < 6, exchange these two values. After the exchange, find its parent node arr[(1-1)/2]=3 through the subscript. Because 3 < 6, exchange these two values. The tree structure changes to:
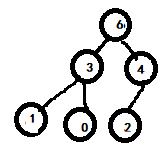
Then access arr[4]=0 and find its parent node arr[(4-1)/2]=3 through subscript. Because 3 > 0, it will not be processed. Then access the next node arr[5]=4 and find its parent node arr[(5-1)/2]=2 through the subscript. Because 2 < 4, exchange these two values. After the exchange, find its parent node arr[(2-1)/2]=6 through the subscript. Because 6 > 4, it will not be processed. The tree structure changes to:
Code implementation:
void heapInsert(int *arr,int len)
{
for(int i =1;i<len;++i)
{
int index = i;//First mark the index of the data to be inserted as index
while(index >= 0 && arr[index]>arr[(index-1)/2])//If the child is greater than the parent and the subscript does not cross the boundary
{
arr[index]=arr[index]^arr[(index-1)/2];
arr[(index-1)/2]=arr[index]^arr[(index-1)/2];
arr[index]=arr[index]^arr[(index-1)/2];//exchange
index=(index-1)/2;//Follow the new index to ensure access to the parent node
}
}
}Node deletion
First, consider how to operate when the root node changes. As shown below:

6 becomes 1. At this time, the downward adjustment method is adopted. The specific process is as follows: first, through the subscript 0 of arr[0], find the largest of the two children of left arr[(2x0+1)] and right (arr[2x0+2]), that is, arr[1]=5. Obviously, 5 > 1, exchange the two values, and the tree becomes
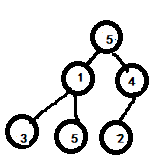
Then, through the subscript 1 of arr[1], find the largest of the two children of left arr[(2x1+1)] and right (arr[2x1+2]), that is, arr[5]=5. Obviously, 5 > 1, exchange the two values, and the tree becomes:
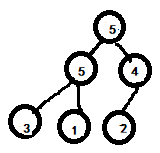
Complete the adjustment.
According to the above process, when we want to delete the root node, we only need to delete the root node, put the last node in the root node position, and then use the above method to adjust.
Code implementation:
void heapify(int arr[], int len)//After modifying the top element of the large root heap, rebuild the large root heap
{
int index = 0;//The top element of the heap is the element with the index 0 of the array, that is, the first element
int left = index * 2 + 1;//Left child
int right = index * 2 + 2;//Right child
while (left<len)//When the left child is greater than or equal to the length of the entire array, it indicates that the array (heap) has been accessed
{
int large = right<len&&arr[right]>arr[left] ? right : left;//Judge which element of the left subtree and the right subtree is larger when the subscript of the right subtree does not cross the boundary,
large = arr[large] > arr[index] ? large : index;//See which is bigger than arr[larg]e or arr[index]
if (large == index)break;//If the subscripts are the same, it means that the two numbers are the same, that is, the maximum number is located on the parent node of the left and right child nodes. At this time, you can directly jump out of the loop without comparing down
int temp = arr[large];
arr[large]=arr[index];
arr[index]=temp;//Exchange data
index = large;//Update the index to the subscript of the largest node. Next, update the left and right children of this node
left = index * 2 + 1;
right = index * 2 + 2;
}
}
void deleteNode(int *arr,int len)
{
int temp = arr[0];
arr[0] = arr[len];
arr[len]=temp;//Exchange stack head and tail
len--;//Data length - 1
heapify(arr,len);//adjustment
}5.2 heap sorting algorithm
How to implement heap sorting? From big root pile to small root pile, as long as the top of big root pile is always the largest and the top of small root pile is always the smallest. Therefore, to realize heap sorting, you only need to put the data into the heap, and then similar to the deletion process. Each time, put the data at the end of the array in the head and adjust it.
Sample program:
void heapInsert(int arr[], int index)//Put the index element of the array into the large root heap
{
while (arr[index] > arr[(index - 1) / 2])//If the child data is greater than the parent data
{
//Exchange parent-child data
int temp = arr[index];
arr[index] = arr[(index - 1) / 2];
arr[(index - 1) / 2] = temp;
//And change the subscript of the element into the subscript of its parent node, so that the parent node can be accessed upward all the time
index = (index - 1) / 2;
}
}
void heapify(int arr[], int len)//After modifying the top element of the large root heap, rebuild the large root heap
{
int index = 0;//The top element of the heap is the element with the index 0 of the array, that is, the first element
int left = index * 2 + 1;//Left child
int right = index * 2 + 2;//Right child
while (left<len)//When the left child is greater than or equal to the length of the entire array, it indicates that the array (heap) has been accessed
{
int large = right<len&&arr[right]>arr[left] ? right : left;//Judge which element of the left subtree and the right subtree is larger when the subscript of the right subtree does not cross the boundary,
large = arr[large] > arr[index] ? large : index;//See which is bigger than arr[larg]e or arr[index]
if (large == index)break;//If the subscripts are the same, it means that the two numbers are the same, that is, the maximum number is located on the parent node of the left and right child nodes. At this time, you can directly jump out of the loop without comparing down
int temp = arr[large];
arr[large]=arr[index];
arr[index]=temp;//Exchange data
index = large;//Update the index to the subscript of the largest node. Next, update the left and right children of this node
left = index * 2 + 1;
right = index * 2 + 2;
}
}
void heapsort(int arr[], int len)
{
for (int i = 1; i < len; ++i)//arr[0] is the root node
{
heapInsert(arr, i);
}//Build a large root heap
len--;
int temp = arr[len];
arr[len] = arr[0];
arr[0] = temp;//First swap the top element with the last element
while (len)
{
heapify(arr, len);//Rebuild large root heap
len--;
int temp = arr[len];
arr[len] = arr[0];
arr[0] = temp;//Then exchange the new top element with the new last element
}
}6. Counting and sorting
For a group of data, their maximum value is N, then we will prepare N+1 buckets (numbered 0~N), and the initial data in the bucket is 0. Then we traverse the array. When the array element is equal to the corresponding number of the bucket, the data of the corresponding number will be + 1. After traversing the array, write the data in the bucket to the source data in turn.
As shown in the figure:
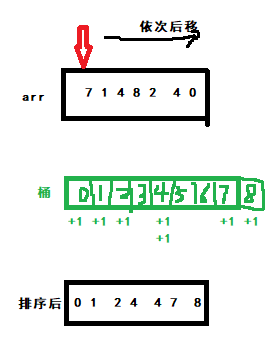
Program instance:
void countSort(int *arr,int len)
{
//Find the maximum value in the array
int max=arr[0];
for(int i =1;i<len;++i)
{
max=max>arr[i]?max:arr[i];
}
//Arrange max+1 bucket
int *bucket = new int[max+1];
memset(bucket,0,4*(max+1));
//Bucket count: the label of the bucket is the data in the ARR, the content of the bucket is the number of a certain data, and when the inner barrel of a certain label is 0, it indicates that there is no data corresponding to the label in the arr.
for(int i=0;i<len;++i)
{
bucket[arr[i]]++;
}
//Dump bucket data to source array
int j=0;
for(int i =0;i<=max;++i)
{
while(bucket[i]--)//When the data in the bucket is 0, it indicates that there is no corresponding data in the arr in the bucket
arr[j++]=i;//When there is data in the bucket, cycle to assign the bucket label to arr, because the pain label is the data in arr
}
}7. Cardinality sorting
Cardinality sorting is actually an optimization of counting sorting. Obviously, when the maximum value in a group is very large, the overhead of using counting sorting is very large. And a serious waste of space. How to avoid this problem, we adopt the idea of cardinality sorting: cardinality sorting can be divided into LSD (sorting from low to high) and MSD (sorting from high to low). Next, I will use LSD to explain the cardinality sorting process.
Cardinality sorting is to give the highest "digit" of this group of data in order, which is used to represent "single digit bucket", "ten digit bucket", "hundred digit bucket",... "Highest digit bucket". The label of the barrel is only 0 ~ 9
Take the following group as an example:
123 , 234,564 , 765, 876,324,651,874,432
Sort from low to high:
First, prepare the low-level bucket, numbered 0 ~ 9, and put each number in the array into the bucket according to the number of digits, as shown in the following figure:

Then pour the data in the bucket into the array in turn:
651 432 123 234 564 324 874 765 876.
Next, prepare a ten digit bucket numbered 0 ~ 9, and put each number in the array into the bucket according to the ten digits, as shown in the following figure:
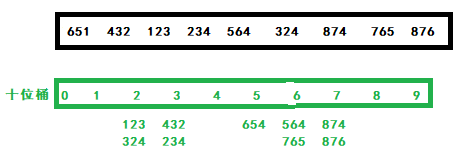
Then pour the ten bit bucket data into the array in turn:
123 324 432 234 654 564 765 874 876.
Next, prepare the hundred digit bucket, numbered 0 ~ 9, and put each number in the array into the bucket according to the hundred digits, as shown in the following figure:
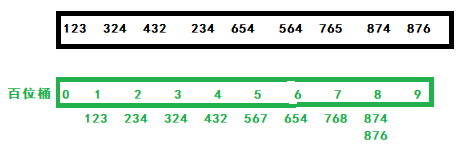
Then pour the data in the 100 bit bucket into the array in turn:
123 234 324 432 564 654 765 874 876.
Finish sorting.
Algorithm steps:
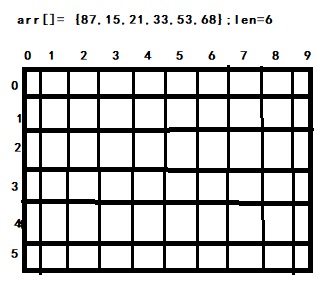
<1> Using a dynamic two-dimensional array, lenx10 dimension, len represents the length of the array, 10 represents 10 buckets, then lenx10 represents 10 buckets, and the maximum number of len in each bucket. The two-dimensional array is used to represent a two-dimensional bucket, and the initial value is 0. Take a simple array as an example:
As shown in the figure:
<2> Obtain the number of bits corresponding to the maximum value of the array. For example, the number of bits corresponding to 423 is 3. The number of digits corresponding to 54 is 2. The maximum number of digits in the figure above is 2
<3> Put the data in the array into the bucket according to the number of bits. The rules of release are:
- Traverse the array. When traversing, obtain the "digit value" of each number, such as when arr[0]=87, ”The one digit value "is 7. Then put 87 in position 0 of bucket 7, that is, the position (0,7) of the two-dimensional array. In turn, arr[1]=15 is placed in position (1,5) of the two-dimensional array. arr[2]=21 - > (2,1); arr [3] = 33 - > (3,3); arr [4] = 53 - > (4,3); arr [5] = 68 - > (5,8); and then put the elements in the bucket back into the source array. As shown in the figure:
-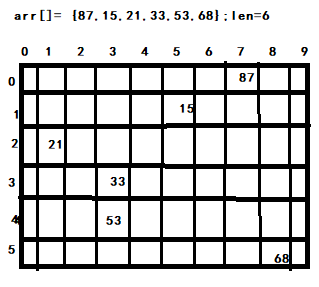
Take the data out of the bucket and put it into arr, then arr={21,33,53,15,87,68};
<4> Enter the ten digits to sort the buckets, and the method is the same as < 3 >. Empty the bucket before putting data.
Note: we need to use a variable to guarantee the number of cycles
Sample program
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include <math.h>
using namespace std;
//LSD is used to sort from low to high
int getMaxWei(int arr[],int len)//Get the number of bits corresponding to the largest number in arr
{
int max = arr[0];
for (int i = 1; i < len; ++i)
max = max>arr[i] ? max : arr[i];
int re = 1;//At least one
while (max/=10)
re++;
return re;
}
void radixSort(int arr[], int len)
{
//Create a two-dimensional array len*10 on the heap, indicating that there are 10 buckets, and each bucket has a maximum of len elements
int** bucket = new int*[len];
for (int i = 0; i < len; ++i)
bucket[i] = new int[10];
//Get the highest number of digits corresponding to the maximum value in arr
int maxHigh = getMaxWei(arr, len);
maxHigh = pow(10, (maxHigh-1));//Change the highest bit to 10 ^ (maxHigh-1), that is, when the highest bit is 3, maxHige=100
int n = 1;//Represents the number of cycles, which is determined by the highest number of digits
while (n<=maxHigh)
{
for (int i = 0; i < len; ++i)
{
for (int j = 0; j < 10; ++j)
{
bucket[i][j] = 0;//The data in the initialization bucket is 0, and the value should be non arr data
}
}
//Fill in the corresponding data in the barrel arr
for (int i = 0; i < len; ++i)
{
int bucket_lieIndex = (arr[i] / n) % 10;
bucket[i][bucket_lieIndex] = arr[i];
}
//Recover the data in the bucket to arr in turn
int k = 0;//The subscript of the array each time the array is restored
for (int i = 0; i < 10; ++i)
{
for (int j = 0; j < len; ++j)
{
if (bucket[j][i]!=0)//bucket[j][i] is not equal to the initialization data in the bucket
{
arr[k++] = bucket[j][i];
}
}
}
n *= 10;//Raise one digit
}
//Free up space
for (int i = 0; i < len; ++i)
delete[] bucket[i];
delete[] bucket;
}
int main(void)
{
int arr[] = {2,32,54,321,54,76,990,53,43 };
radixSort(arr, sizeof(arr) / 4);
for (int i = 0; i < sizeof(arr) / 4; ++i)
{
cout << arr[i] << endl;
}
return 0;
}