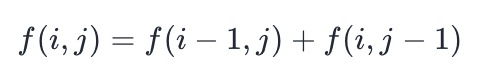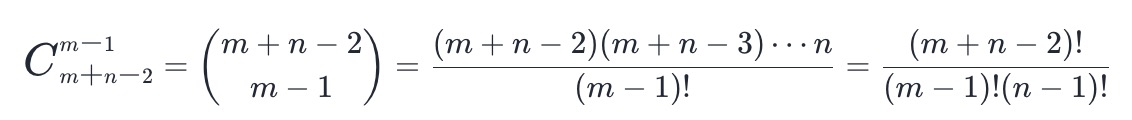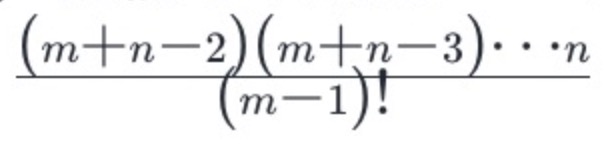1, Title Requirements

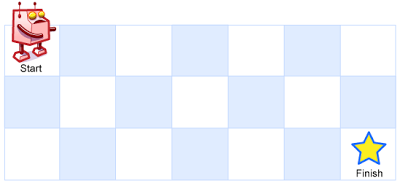
• A robot is located in the upper left corner of an m x n grid (the starting point is marked as "Start" in the figure below). The robot can only move down or right one step at a time. The robot tries to reach the lower right corner of the grid (marked as "Finish" in the figure below). How many different paths are there in total?
• Example 1:

Input: m = 3, n = 7
 Output: 28

• Example 2:

Input: m = 3, n = 2
 Output: 3
 Explanation:
Starting from the upper left corner, there are three paths to the lower right corner.
1. towards the right -> down -> down
2. down -> down -> towards the right
3. down -> towards the right -> down

• Example 3:

Input: m = 7, n = 3
 Output: 28

• Example 4:

Input: m = 3, n = 3
 Output: 6

• Tips:
• • 1 <= m, n <= 100；
• • The question data ensures that the answer is less than or equal to 2 * 109.

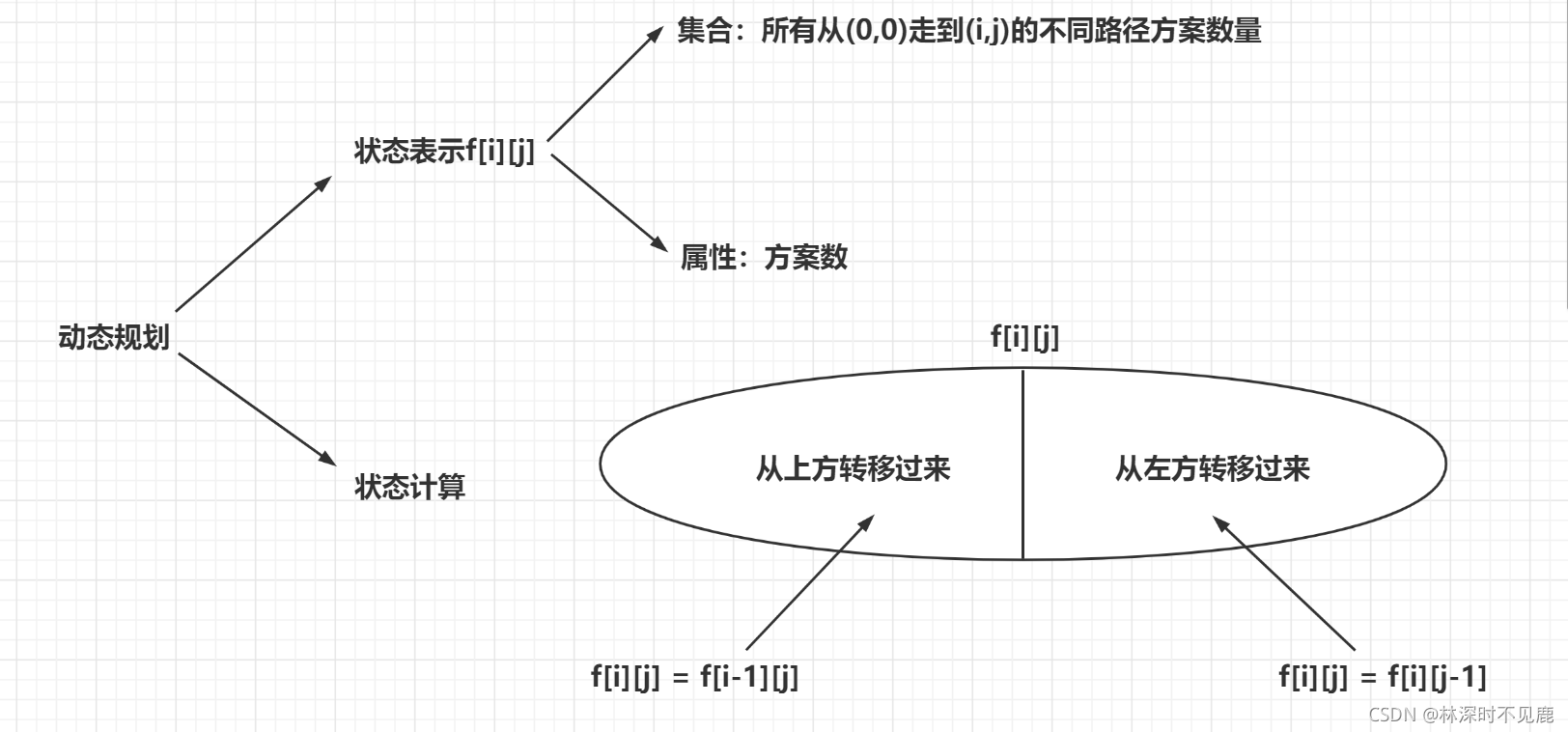
2, Solving algorithm

① Dynamic programming

• Use f(i,j) to indicate the number of paths from the upper left corner to (i,j), where the ranges of i and j are [0,m) and [0,n). Since each step can only move down or right one step, if you want to go down one step, you will come from (i − 1,j); if you go right one step, you will come from (i,j − 1).
• f[i,j] represents the number of schemes of all different paths from (0,0) to (i,j), then f[m-1][n-1] represents the number of schemes of all different paths from the upper left corner of the grid to the lower right corner of the grid, which is the answer:

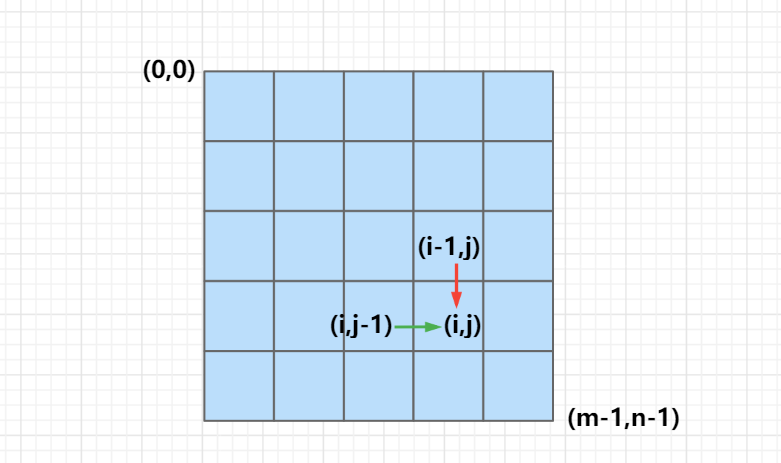
• There are two paths to (i,j) due to the restriction that you can only go down or right:
• • Transfer from above, f[i][j] = f[i-1][j];
• • Transfer from the left, f[i][j] = f[i][j-1];
• Therefore, the dynamic programming transfer equation can be written to add the number of schemes of the right and down paths:

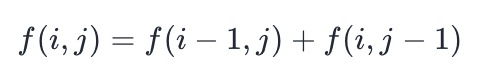
• It should be noted that if i=0, then f(i − 1,j) is not a state that meets the requirements, and this item needs to be ignored; Similarly, if j=0, then f(i,j − 1) is not a state that meets the requirements, and this item should also be ignored.
• The initial condition is f(0,0)=1, that is, there is a way from the upper left corner to the upper left corner. There is only one path from (0,0) to (0,0):

• The final answer is f(m − 1,n − 1).
• For the convenience of code writing, all f(0,j) and f(i,0) can be set as boundary conditions, and their values are 1.
• Java example:

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] f = new int[m][n];
        for (int i = 0; i < m; ++i) {
            f[i][0] = 1;
        }
        for (int j = 0; j < n; ++j) {
            f[0][j] = 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
}

• C + + example:

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            f[i][0] = 1;
        }
        for (int j = 0; j < n; ++j) {
            f[0][j] = 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
};

② Combinatorial mathematics

• From the upper left corner to the lower right corner, you need to move m+n − 2 times, including m − 1 downward movement and N − 1 right movement. Therefore, the total number of paths is equal to the number of schemes selected from m+n − 2 downward movements, that is, the number of combinations:

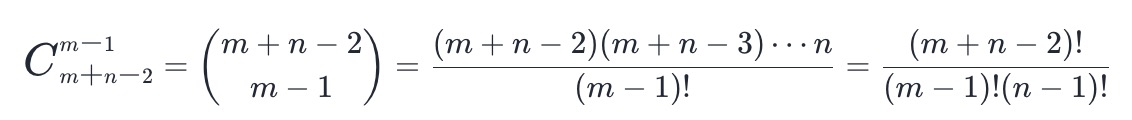
• Therefore, the combination number can be calculated directly. There are many calculation methods:
• • If the language used has an API for combination number calculation, you can call API calculation;
• • If there is no corresponding API, it can be calculated as follows:

• C + + example:

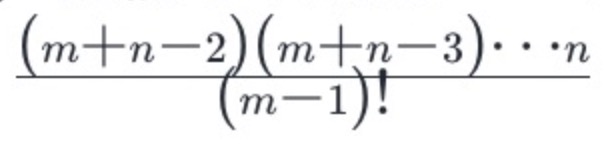
class Solution {
public:
    int uniquePaths(int m, int n) {
        long long ans = 1;
        for (int x = n, y = 1; y < m; ++x, ++y) {
            ans = ans * x / y;
        }
        return ans;
    }
};

• Java example:

class Solution {
    public int uniquePaths(int m, int n) {
        long ans = 1;
        for (int x = n, y = 1; y < m; ++x, ++y) {
            ans = ans * x / y;
        }
        return (int) ans;
    }
}

③ Recursion

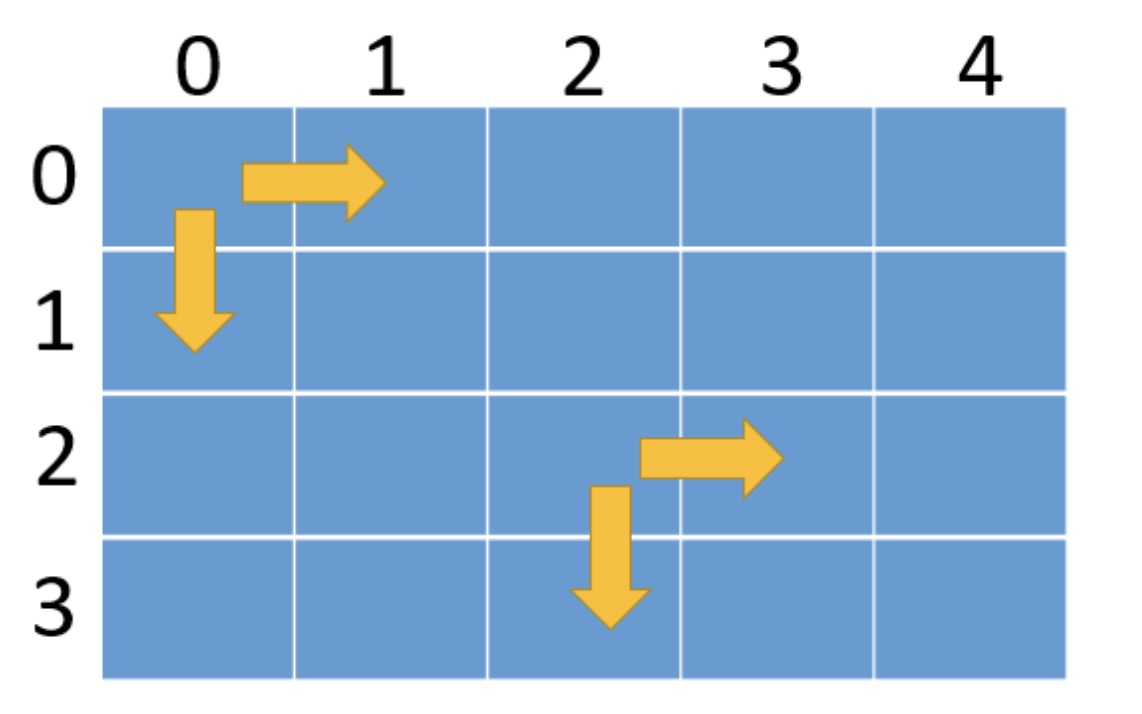
• Since the robot can only move down or right one step at a time, for position (i,j), if it wants to move again, it can only go right or down:
• • To the right: i do not move, j+1;
• • Down: j+1, i does not move;

• Then all paths from (0,0) to (m,n) should be combined by two routes:
• • All paths from (0,0) to the right;
• • All paths from (0,0) to the next.
• Adding up the above is the total path, so the core logic of recursion is:

result = dfs(i + 1, j) + dfs(i, j + 1)

• The core logic of recursion has been written, but the termination condition of recursion is missing. When will it terminate? When reaching the boundary, it will trigger recursive termination and then return. The termination condition is when moving to the rightmost column or the bottom row.

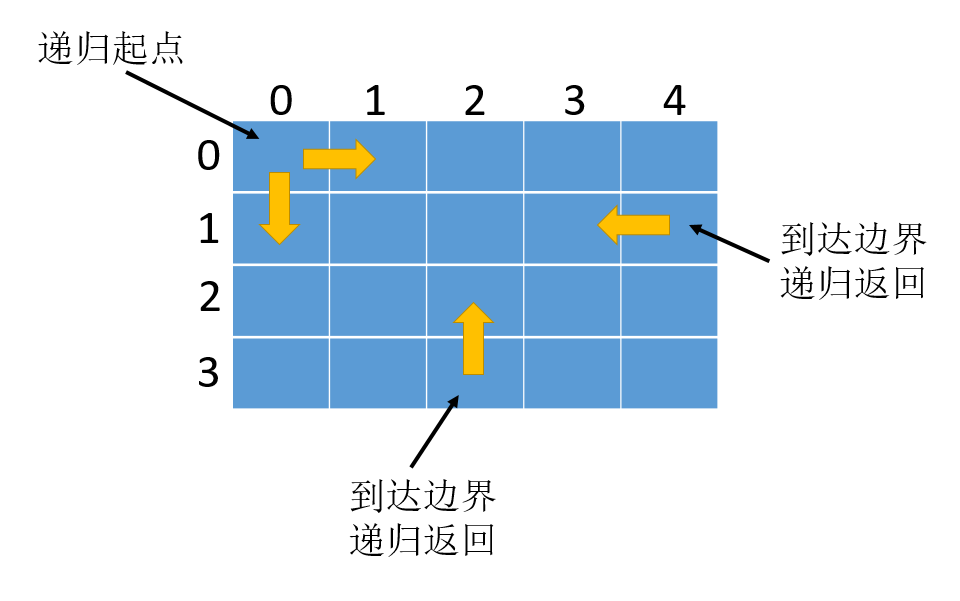
• That is, when i == m - 1, or j == n - 1, recursion returns:

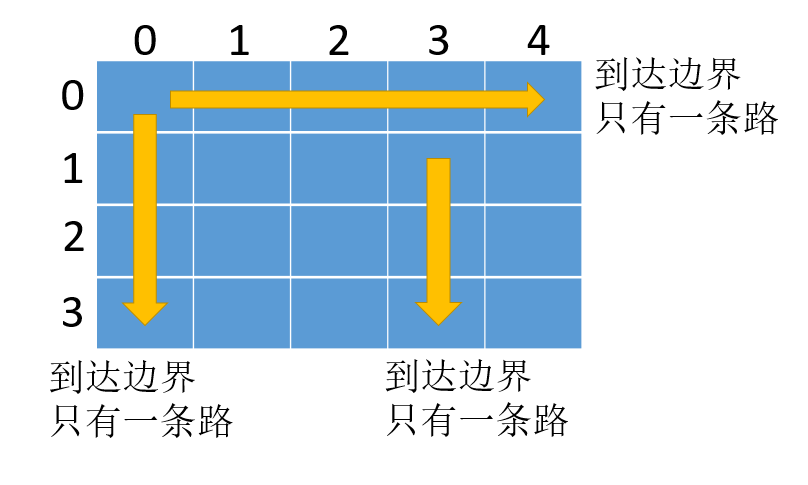
• When you reach the boundary, you can return to 1. If it is in the first column, there is only one way down no matter how; Similarly, if you are in the first row, there is only one way to the right.
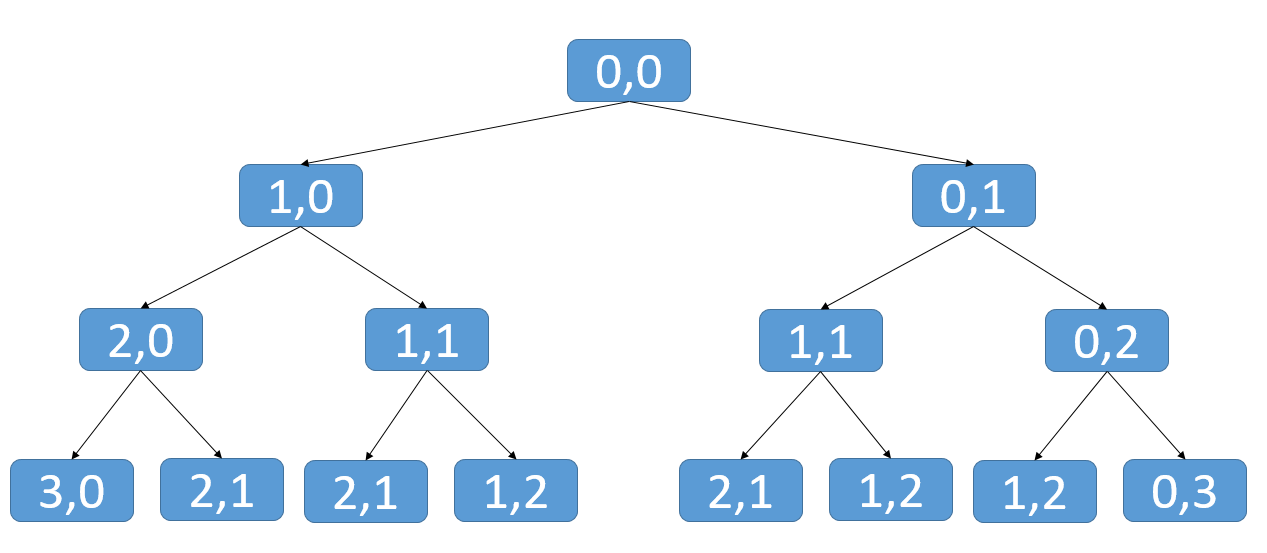
• Of course, pure recursion cannot be used in this problem, because a large number of repeated calls will lead to timeout, as shown in the figure below. When the starting point is (0,0), there will be a large number of repeated calls:

• Java example:

class Solution {
    public int uniquePaths(int m, int n) {
        return dfs(new HashMap<Pair,Integer>(), 0, 0, m, n);
    }

    private int dfs(Map<Pair,Integer> cache, int i, int j, int m, int n) {
        Pair p = new Pair(i,j);
        // Returns directly if (i,j) is in the cache
        if(cache.containsKey(p)) {
            return cache.get(p);
        }
        // When the boundary is reached, return 1
        if(i == m - 1 || j == n - 1) {
            return 1;
        }
        // Continue to call recursively, i+1 down and j+1 right
        cache.put(p, dfs(cache, i + 1, j, m, n) + dfs(cache, i, j + 1, m, n) );
        return cache.get(p);
    }
}