Introduction to particle swarm optimization 03: with Matlab and python code (PSO)
VIII:
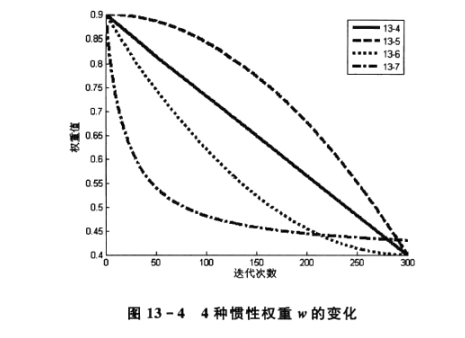
Inertia weight w reflects the ability of particles to inherit the previous velocity. Shi Y first introduced inertia weight w into PSO algorithm, and analyzed and pointed out that a larger inertia weight value is conducive to global search, while a smaller inertia weight value is more conducive to local search. In order to balance the two, a linear decreasing inertia weight (LDIW) is proposed.
Equation (13-4) is wrong. The denominator is only k, and Tmax is removed-
Without inertia weight, let the program run 100 times, and the average value is the optimal result. Improve on the previous code: the function code is the same as the previous section.
%% Double emptying+Close drawing
clc,clear,close all;
%% Perform 100 operations on the program
for k = 1:100
%% PSO Parameter calibration. ***Note: inertia weight is missing here w And dimensions D***
c1 = 1.49445; %Individual learning factor
c2 = 1.49445; %Social learning factor
maxgen = 300; %Number of iterations
sizepop = 20; %Population size
Vmax = 0.5; %Upper and lower limits of speed
Vmin = -0.5;
popmax = 2; %Upper and lower limit of position
popmin = -2;
%% Initialize the position and velocity of each particle in the particle swarm, and calculate the fitness value
for j = 1:sizepop %Self reference for loop
pop(j,:) = 2*rands(1,2); %Self reference rands
V(j,:) = 0.5*rands(1,2);
fitness(j) = fun(pop(j,:)); %Self reference function
end
%% Search for initial individual extremum and group extremum
%{
***be careful: pop Is a matrix of 20 rows and 2 columns, of which the first column is X1，The second column is X2；V Also
fitness If there is a great God who understands, please explain in the comment area. What I understand is a matrix with 20 rows and 1 column, so as to find the position of the extreme value of the group,
But the program does give a matrix of 1 row and 20 columns***
--------------------------------------------------------------------------------------------
There are many things to pay attention to here matlab Medium max The reference blog doesn't say that
Through experiments, it is found that when the matrix A Is a row vector,[maxnumber maxindex] = max(A)in maxindex The column of the maximum value is returned
This explains the question just now!
A=[1,2,3,4,8,6,75,9,243,25]
A =
1 2 3 4 8 6 75 9 243 25
[maxnumber maxindex] = max(A)
maxnumber =
243
maxindex =
9
--------------------------------------------------------------------------------------------
%}
[bestfitness bestindex] = max(fitness); %Self reference max Function usage
zbest = pop(bestindex,:); %Group extreme position
gbest = pop; %The individual extreme position is initialized, so the individual extreme position of each particle is its own random position
fitnessgbest = fitness; %Individual extreme fitness value
fitnesszbest = bestfitness; %Population extreme fitness value
%% Optimization iteration
for i = 1:maxgen
%Speed update
for j = 1:sizepop
V(j,:)=V(j,:)+c1*rand*(gbest(j,:)-pop(j,:))+c2*rand*(zbest-pop(j,:)); %Inertia weight is not added
V(j,find(V(j,:)>Vmax)) = Vmax; %find The function returns the index here. There are three cases: 1; 2； 1 2；
V(j,find(V(j,:)<Vmin)) = Vmin;
%Location update
pop(j,:)=pop(j,:)+V(j,:);
pop(j,find(pop(j,:)>popmax)) = popmax;
pop(j,find(pop(j,:)<popmin)) = popmin;
%Update fitness value
fitness(j)=fun(pop(j,:));
end
%Individual extremum update
for j = 1:sizepop
if fitness(j)>fitnessgbest(j)
gbest(j,:)=pop(j,:);
fitnessgbest(j)=fitness(j);
end
%Population extremum update
if fitness(j)>fitnesszbest
zbest=pop(j,:);
fitnesszbest=fitness(j);
end
end
%Each generation records to the optimal extreme value result in
result(i)=fitnesszbest;
end
G(k) = max(result);
end
GB = max(G); %The largest optimal solution among all the optimal solutions after 100 runs
Average = sum(G)/100; %Average of all optimal solutions
Fnumber =length(find(G>1.0054-0.01&G<1.0054+0.01));%Number of optimal solutions within the error range
FSnumber =length(find(G>1.0054+0.01|G<1.0054-0.01));%Number of optimal solutions outside the error range
precision = Fnumber/100 %Solution accuracy
It can be found that the evaluation of the optimal solution is very unstable:
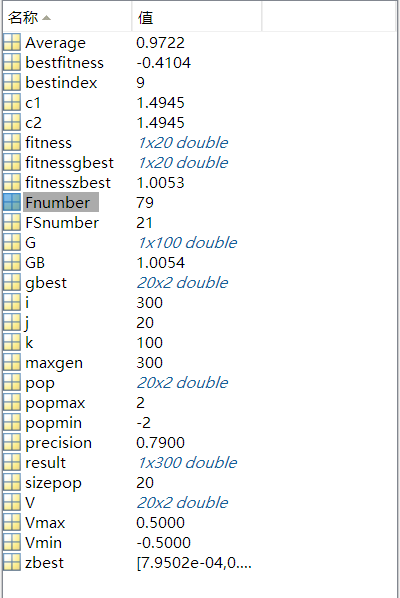There are only 79 times to find the optimal solution, and there are 21 times left. Thus, inertia weight is very important. Here is a direct conclusion:
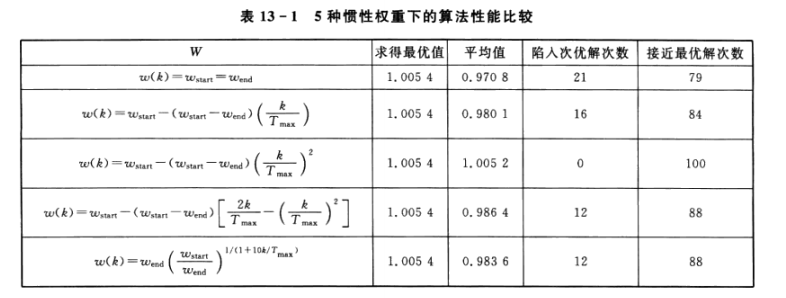
It can be seen that the effect of the second inertia weight is the best, that is, formula (13-5). Here, I tested it later and found that no matter what kind of inertia weight, I can't get the above conclusion.
Reference: analysis of 30 cases of matlab intelligent algorithm (Second Edition)
My experimental conclusions are as follows:
On the whole, formula 4 is the best, but after many experiments, you will find that each w has a wide range of accuracy (the number of experiments with the optimal solution / the number of experiments),
Therefore, there is no best choice for inertia weight here. For specific problems, you can increase the number of code runs for specific experiments, and finally take the best value.
The code is divided into two parts. The original code of some references has errors in its inertia weight and lacks w
The other part is to modify the code for myself
Connection source code
https://download.csdn.net/download/weixin_42212924/18839919
Previous PSO articles
https://blog.csdn.net/weixin_42212924/article/details/116808786
https://blog.csdn.net/weixin_42212924/article/details/116947153