Notice before reading
Key points introduction and brief statement.
The seventh computer question is be ing updated
Topic content
Problem description
The main office and scientific research buildings of Beihang include new main building, Yifu Building, such as heart building, office building, library, main building, building 1, etc;. Beihang network center plans to lay optical cables between relevant buildings for network connectivity. Please give the laying scheme with the least materials.
Write a program, input a distribution map of office area and the distance between buildings, and calculate the laying scheme with the least materials (there is only one set of optimal solutions, without considering multiple sets of solutions). Prim or Kruskal algorithm is required.
Input form
The vertices (i.e. buildings) of the office area distribution map are numbered according to the natural number (0, 1, 2, n-1). First input two positive integers from the standard input to represent the number of vertices and edges of the circuit diagram respectively, and then input the information of each edge in the next line. Each edge occupies one line. The specific form is as follows:
< n> < e>
< id> < vi> < vj> < weight>
...
That is, the weight of the edge between vertices vi and vj is weight, and the number of the edge is id.
Output form
Output the minimum number of materials used for laying optical cables, and then output the id of the side to be laid from another line, and the output id value is output in ascending order.
Sample
6 10 1 0 1 600 2 0 2 100 3 0 3 500 4 1 2 500 5 2 3 500 6 1 4 300 7 2 4 600 8 2 5 400 9 3 5 200 10 4 5 600
[sample output]
1500 2 4 6 8 9
Example description
The sample input shows that the distribution map has 6 vertices and 10 edges; There is an edge between vertices 0 and 1. The number of the edge is 1 and the weight is 600; There is an edge between vertices 0 and 2, with a weight of 100, and so on. The corresponding figure is as follows:
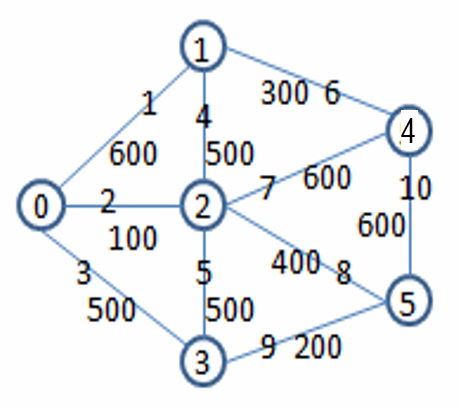
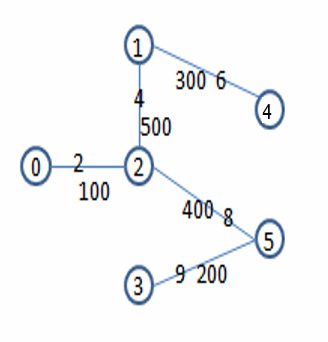
After calculation, the minimum material of this graph is 1500, which can make the graph connected, and the number of edges is 24689. The corresponding minimum spanning tree is as follows:
Problem solution
Think and explain in detail
We can use Prim and kruskal to solve this problem. If you want to know the principle of these two solutions, you can expand the plate step by step.
This problem is the most basic algorithm problem of minimum spanning tree. It is not difficult to operate step by step.
Prim
Reference code
Prim
#include<stdio.h>
#include<stdlib.h>
#define M 101
#define INF 0x3f3f3f3f
int sum,top=0,MinSpanTreeVertex[200],egdesID[200][200];
// MinSpanTreeVertex stores the path vertex ID, and egdesID stores the path ID between two vertices
void MinSpanTree_Prim(int weights[][M],int vertexNum,int FirstVertexID,int *edges);//Prim algorithm
int cmp (const void * a, const void * b);
int main()
{
int weights[M][M],edges[M];
int i,j,k,vertexNum,edgeNum,ID;
int v1,v2,w;
scanf("%d %d",&vertexNum,&edgeNum); //Number of vertices and edges
for(i=0;i<vertexNum;i++)
for(j=0;j<vertexNum;j++)
weights[i][j]=INF; //initialization
for(i=0;i<edgeNum;i++)
{
scanf("%d %d %d %d",&ID,&v1,&v2,&w); //Input information
egdesID[v1][v2]=ID;
egdesID[v2][v1]=ID;
weights[v1][v2]=w;
weights[v2][v1]=w;
}
MinSpanTree_Prim(weights,vertexNum,0,edges); //minimum spanning tree
qsort(MinSpanTreeVertex,top,sizeof(int),cmp); //Sort as required
printf("%d\n",sum);
for(i=0;i<vertexNum-1;i++)
printf("%d ",MinSpanTreeVertex[i]); //output
return 0;
}
//Minimum spanning tree -- Prim algorithm (starting from 0)
void MinSpanTree_Prim(int weights[][M],int vertexNum,int FirstVertexID,int *edges)
{// weights is the weight array, vertexNum is the number of vertices, FirstVertexID is the first node of the smallest number, and edges is the smallest spanning tree edge
int min,minweight[M];
int i,j,k;
for(i=0;i<vertexNum;i++) //Initialize correlation array
{
minweight[i]=weights[FirstVertexID][i]; //Store the weights of the first vertex and its edge into the array
edges[i]=FirstVertexID; //Initialize first vertex
}
minweight[FirstVertexID] = 0; //Add the first vertex to the spanning tree. 0 means that the vertices in the corresponding table below have been added to the tree
for(i=1;i<vertexNum;i++)
{
min=INF;
for(j=0,k=0;j<vertexNum;j++)
if(minweight[j]!=0 && minweight[j]<min)
{
min = minweight[j];
k=j; //Find the minimum value in the array with the subscript k
}
sum+=minweight[k];
minweight[k] = 0;//Find a new vertex of the minimum spanning tree
//printf("%d ",egdesID[k][edges[k]]);
MinSpanTreeVertex[top]=egdesID[k][edges[k]]; //Record vertex information
top++;
for(j=0;j<vertexNum;j++) //Check the weight between the newly added vertex k and the non added vertex in turn
if(minweight[j]!=0 && weights[k][j] < minweight[j])
{
minweight[j]=weights[k][j]; //Replace operation
edges[j]=k;
}
}
}
int cmp (const void * a, const void * b)
{
return *(int*)a - *(int*)b;
}
kruskal
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<stdlib.h>
#include<ctype.h>
#include<stdbool.h>
struct edge //Edge structure
{
int ID; //Path ID
int u,v; //Two vertices
int w; //weight
};
struct edge edges[600100];
int i,top=0;
int Father[10100],MinSpanTreeVertex[2000];
//Father stores the earliest (ancestor) vertex of each vertex, and MinSpanTreeVertex stores the path vertex ID
int cnt;
long long res; //result
//Minimum spanning tree -- Kruskal algorithm (joint search set)
void initFather(int vertexNum)
{
int i;
for(i=1;i<=vertexNum;++i)
{
Father[i]=i; //Initial conversation ancestor array (at the beginning, it is its own number)
}
}
int getFather(int x)
{
return Father[x]==x?x:(Father[x]=getFather(Father[x])); //Fallback ancestors
}
void kruskal(int vertexNum,int edgeNum)
{
int p,q;
cnt=0,res=0;
for(i=0;i<edgeNum;++i)
{
p=getFather(edges[i].u); //Back to ancestors
q=getFather(edges[i].v); //Back to ancestors
if(p!=q) //If the ancestors are different (i.e. there is no closed loop)
{
Father[p]=q; //Update ancestors
MinSpanTreeVertex[top++]=edges[i].ID; //Enter node information
res+=edges[i].w; //Plus the cost
cnt++; //Tree node + 1
}
if(cnt==vertexNum-1) //Meet the conditions
{
break;
}
}
}
int cmp(const void*p1,const void*p2) //Sort by weight
{
struct edge *a=(struct edge*)p1;
struct edge *b=(struct edge*)p2;
return a->w-b->w;
}
int cmp2 (const void * a, const void * b) //Sort by size
{
return *(int*)a - *(int*)b;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
initFather(n); //Initialize ancestor array
int i;
for(i=0;i<m;i++)
scanf("%d %d %d %d",&edges[i].ID,&edges[i].u,&edges[i].v,&edges[i].w);
qsort(edges,m,sizeof(struct edge),cmp);
kruskal(n,m);
printf("%d\n",res);
qsort(MinSpanTreeVertex,top,sizeof(int),cmp2); //sort
for(i=0;i<n-1;i++)
printf("%d ",MinSpanTreeVertex[i]); //output
}
Supplementary test data
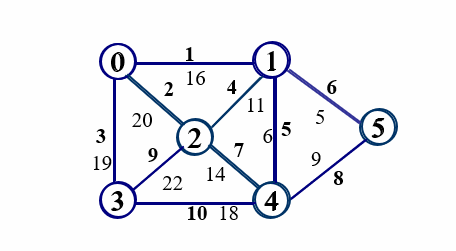
[sample input]
6 10 1 0 1 16 2 0 2 20 3 0 3 19 4 1 2 11 5 1 4 6 6 1 5 5 7 2 4 14 8 4 5 9 9 2 3 22 10 3 4 18
[sample output]
56 1 4 5 6 10
Principle interpretation
Prim algorithm
Time complexity: O (N^2) (N is the number of vertices)
prim algorithm, also known as "point adding method", is used for weighted undirected connected graphs with more edges
Methods: find the vertex with the smallest connection weight every time (greedy), and add the point to the minimum spanning tree set until all points are accessed (BFS access).
Note: any one of the same weights can be selected, but the closed loop is not allowed.
Start operation: 1 Select any point at first (because all the last points will be in the minimum spanning tree, so you can choose any point).
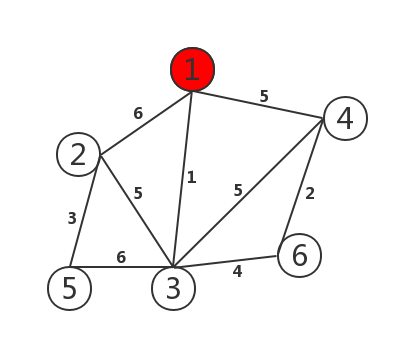
2. Compare the edges (1, 5, 6) of point 1 and select the edge with weight 1
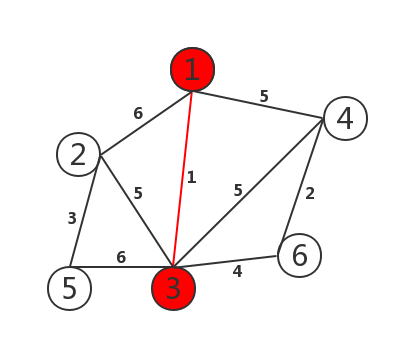
3. Compare the edges of points 1 and 3 (4, 5, 5, 5, 6, 6) and select the edge with weight of 4.
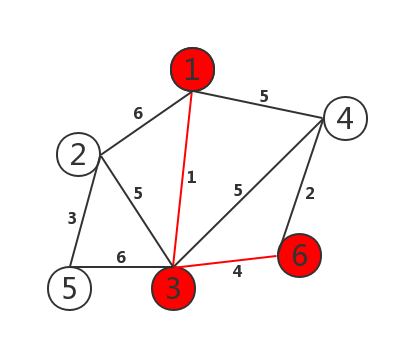
4. Compare the edges of points 1, 3 and 6 (2, 5, 5, 5, 6 and 6), and select the edge with weight of 2.
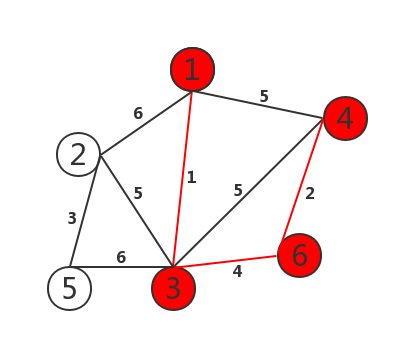
5. Compare the edges of points 1, 3, 4 and 6 (5, 6 and 6), and select the vertex edge with weight of 5
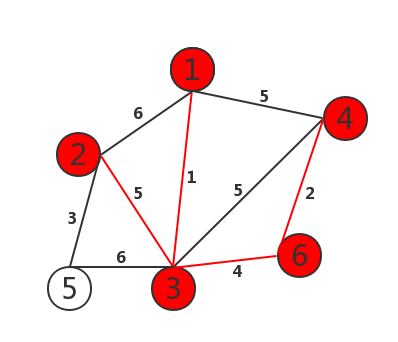
5. Compare the edges of points 1, 2, 3, 4 and 6 (3 and 6), and select the vertex edge with weight of 3
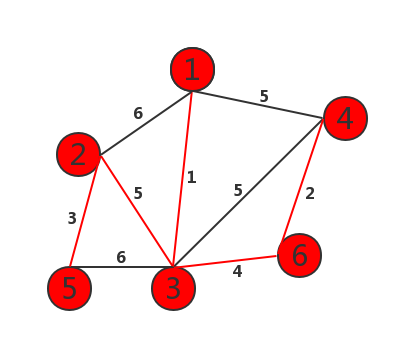
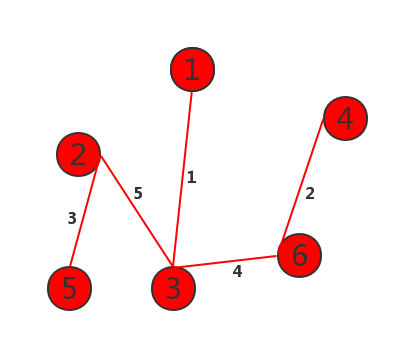
6. Complete the construction
kruskal algorithm
Time complexity: O (NlogN) (N is the number of edges)
kruskal algorithm, also known as "edge addition method", is used for sparse graphs with fewer edges
Methods: find the edge with the smallest weight in the graph every time, and add the two vertices connected by the edge to the minimum spanning tree set
Note: any one of the same weights can be selected, but it is not allowed to have a closed loop (parallel set search).
Step 1: sort the edges according to their weights
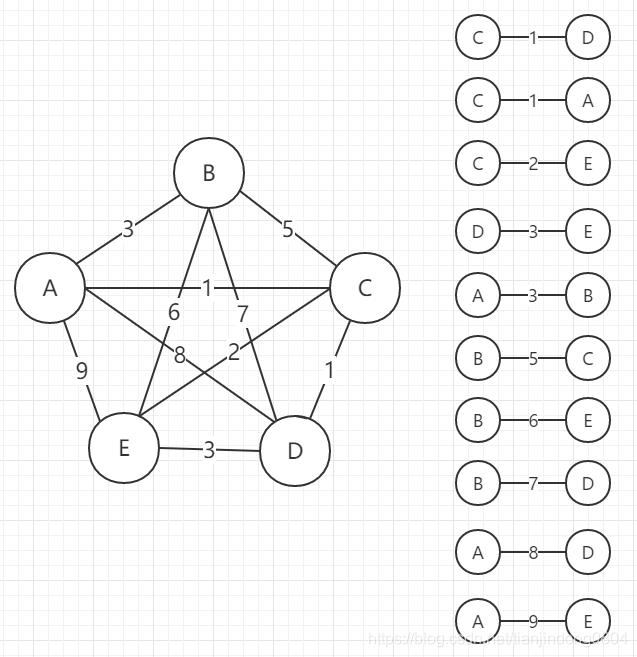
Step 2: take out the edges from top to bottom. If the edges taken each time form a loop in the tree, they must be discarded. Until the last vertex is connected in the tree, the minimum spanning tree is generated.
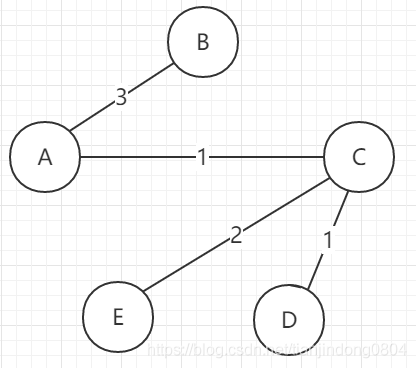
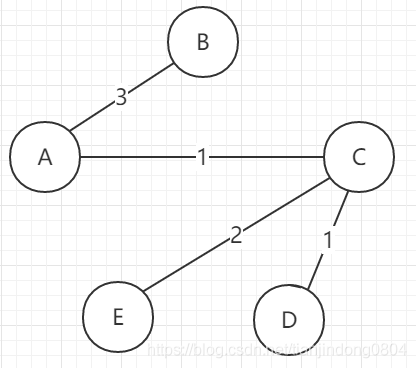
When taking out the edge (D,E), the edge is discarded because it has a loop with (C,D), (C,E).
Here we come to the focus of the problem. How do we judge whether the newly added edge will form a loop? Here we can use and search the set.
Generation of judgment circuit
In the initial state, we regard each node in the graph as a tree, for example:

At this time, we take out the first edge (C,D) in the sorting edge set. We find that the nodes C and d come from different trees, which shows that the addition of this edge will not form a loop. At this time, we need to set the D tree as the subtree of C. For example:
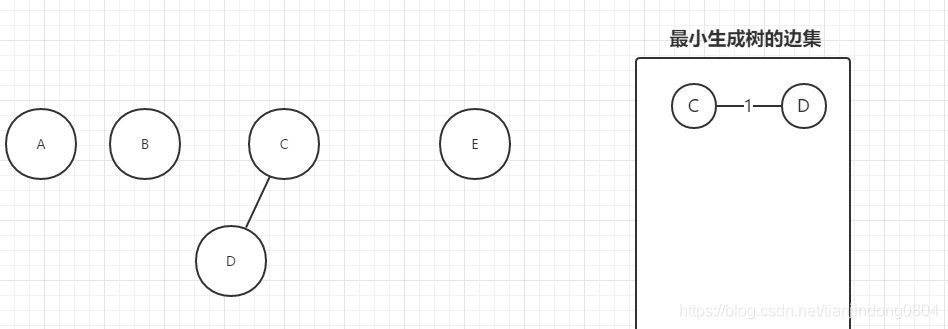
At this time, we take out the second edge (C,A). We find that the nodes C and A belong to different trees, so the addition of (C,A) edge will not form A ring. We add this edge to the edge set of the minimum spanning tree. At this time, we need to set the A tree as the subtree of C, such as:
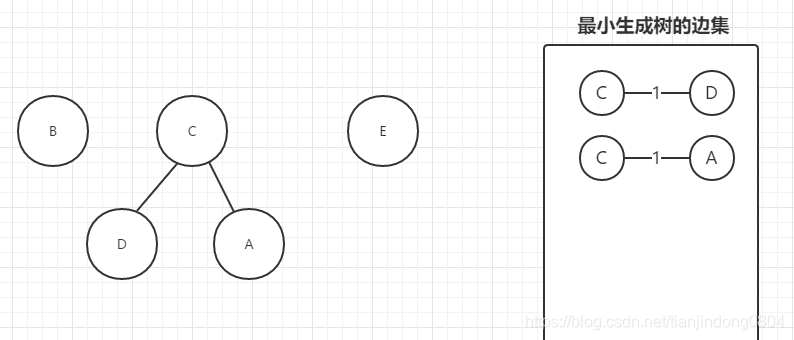
We take out the third edge (C,E) and find that C and e still belong to two different trees, so we still add this edge to the edge set of the minimum spanning tree. Then set E tree as the subtree of C tree, for example:
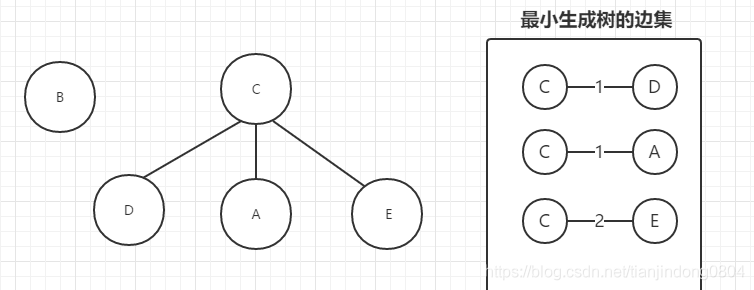
Therefore, if we take out the edge e from the tree (d), we will find that the two edges (d) are from the same tree, so we need to discard the two edges (E) to form the same edge D.
We take out the fifth edge: (A, b) and find that A and B belong to different nodes, which means that the addition of this edge will not form A ring. We add this edge to the edge set of the minimum spanning tree. We found that the number of edges plus one in the edge set is just equal to the number of nodes, which means that each node has been included in the edge set of the minimum spanning tree, so there is no need to continue to take the sorted edge set down.
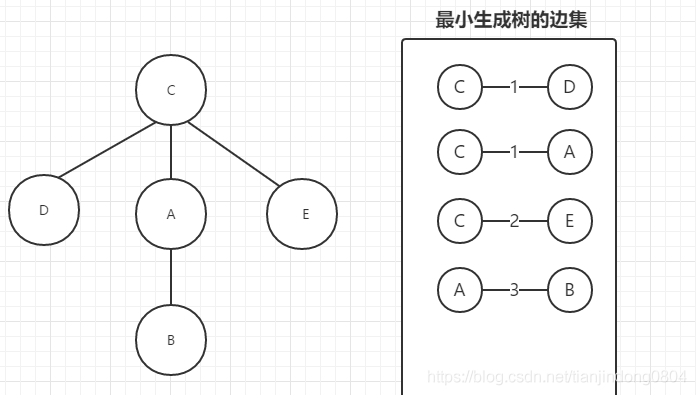
At this time, we reconstruct the edges in the edge set into a graph, that is, a minimum spanning tree:
That's the whole Kruskal idea