preface
Test what you have learned before. Learn how to use templates from the source code.
Definition and use
-
integer_sequence: judge whether it is an integer type. If it is not, the compilation fails (using static assertion). If it is, save its own type and the incoming integer type, as well as the length of variable parameters.
-
index_sequence_for: generates an integer of the specified size_ Sequence type. for example
index_sequence_for<3> —> integer_sequence<size_t, 0, 1, 2, 3>
1, integer_sequence source code
The old rule is to paste the source code first. (to explain, this is the source code of other versions I'm looking for. It's not the same version as the previous version, but the basic implementation is similar. Some of the source code of the previous version can't be found)
// TEMPLATE STRUCT integer_sequence
template<class _Ty,
_Ty... _Vals>
struct integer_sequence
{ // sequence of integer parameters
static_assert(is_integral<_Ty>::value,
"integer_sequence<T, I...> requires T to be an integral type.");
typedef integer_sequence<_Ty, _Vals...> type;
typedef _Ty value_type;
static _CONST_FUN size_t size() _NOEXCEPT
{ // get length of parameter list
return (sizeof...(_Vals));
}
};
// ALIAS TEMPLATE make_integer_sequence
template<bool _Negative,
bool _Zero,
class _Int_con,
class _Int_seq>
struct _Make_seq
{ // explodes gracefully below 0
static_assert(!_Negative,
"make_integer_sequence<T, N> requires N to be non-negative.");
};
template<class _Ty,
_Ty... _Vals>
struct _Make_seq<false, true,
integral_constant<_Ty, 0>,
integer_sequence<_Ty, _Vals...> >
: integer_sequence<_Ty, _Vals...>
{ // ends recursion at 0
};
template<class _Ty,
_Ty _Ix,
_Ty... _Vals>
struct _Make_seq<false, false,
integral_constant<_Ty, _Ix>,
integer_sequence<_Ty, _Vals...> >
: _Make_seq<false, _Ix == 1,
integral_constant<_Ty, _Ix - 1>,
integer_sequence<_Ty, _Ix - 1, _Vals...> >
{ // counts down to 0
};
template<class _Ty,
_Ty _Size>
using make_integer_sequence = typename _Make_seq<_Size < 0, _Size == 0,
integral_constant<_Ty, _Size>, integer_sequence<_Ty> >::type;
template<size_t... _Vals>
using index_sequence = integer_sequence<size_t, _Vals...>;
template<size_t _Size>
using make_index_sequence = make_integer_sequence<size_t, _Size>;
template<class... _Types>
using index_sequence_for = make_index_sequence<sizeof...(_Types)>;
Previous source code__ make_ integer_ The implementation of SEQ template is gone. No way, I found an old version of the source code. But the comparison shows that the known implementation is the same.
template <class _Ty, _Ty... _Vals>
struct integer_sequence { // sequence of integer parameters
static_assert(is_integral_v<_Ty>, "integer_sequence<T, I...> requires T to be an integral type.");
using value_type = _Ty;
_NODISCARD static constexpr size_t size() noexcept {
return sizeof...(_Vals);
}
};
template <class _Ty, _Ty _Size>
using make_integer_sequence = __make_integer_seq<integer_sequence, _Ty, _Size>;
template <size_t... _Vals>
using index_sequence = integer_sequence<size_t, _Vals...>;
template <size_t _Size>
using make_index_sequence = make_integer_sequence<size_t, _Size>;
template <class... _Types>
using index_sequence_for = make_index_sequence<sizeof...(_Types)>;
2, Use steps
1. All analysis
// TEMPLATE STRUCT integer_sequence
template<class _Ty,
_Ty... _Vals>
struct integer_sequence
{ // sequence of integer parameters
static_assert(is_integral<_Ty>::value,
"integer_sequence<T, I...> requires T to be an integral type.");
//is_ integral<_ Ty > judge whether it is an integer, inherited bool type, is_ integral<_ Ty >:: type gets false or true. If it is true, the assertion will not work. If it is false, an error will be reported directly.
typedef integer_sequence<_Ty, _Vals...> type;
//Redefine its own type. Save all variables and their types
typedef _Ty value_type;
//Save type
static _CONST_FUN size_t size() _NOEXCEPT
{ // get length of parameter list
return (sizeof...(_Vals));
}
};
//The size() function can obtain the number of variable variables.
//You can look back and forward. There is a call behind.
//Define a template base class. Filter special cases
// ALIAS TEMPLATE make_integer_sequence
template<bool _Negative,
bool _Zero,
class _Int_con,
class _Int_seq>
struct _Make_seq
{ // explodes gracefully below 0
static_assert(!_Negative,
"make_integer_sequence<T, N> requires N to be non-negative.");
//The first parameter cannot be true. If yes, an error is directly asserted.
};
//Specialize the above base classes. When the first parameter is false and the second parameter is true, it will be called to inherit integer_sequence
template<class _Ty,
_Ty... _Vals>
struct _Make_seq<false, true,
integral_constant<_Ty, 0>,
integer_sequence<_Ty, _Vals...> >
: integer_sequence<_Ty, _Vals...>
{ // ends recursion at 0
};
//The above partial specialization template is again partial specialization. Called when the second parameter is flash.
template<class _Ty,
_Ty _Ix,
_Ty... _Vals>
struct _Make_seq<false, false,
integral_constant<_Ty, _Ix>,
integer_sequence<_Ty, _Vals...> >
: _Make_seq<false, _Ix == 1,
integral_constant<_Ty, _Ix - 1>,
integer_sequence<_Ty, _Ix - 1, _Vals...> >
//This step is the key. Use inheritance to increase the number of parameters. For example, input 3 will eventually become 1,2,3
//_Make_seq<false, _Ix == 1,
//Check whether the second parameter gets 1. If so, call when the above second parameter is true. Send all parameters into integer_sequence
//If not, continue to call itself.
//integral_constant<_Ty, _Ix - 1>,integer_sequence<_Ty, _Ix - 1, _Vals...> >
//integer_ sequence<_ Ty, _ Ix - 1, _ Vals...> Add the number of variable parameters + 1 (_Ix - 1)
//This is why 3 becomes 1,2,3.
//integer_sequence<size_t, 3-1, 3>
//integer_sequence<size_t, 2-1, 2, 3>
//integer_ sequence<size_ t. 1-1, 1, 2, 3 > last 1 = = 1. The second parameter is true
//Therefore, struct is called_ Make_ seq<false, true,integral_ constant<_ Ty, 0>,
//Here will be < size_ t. 0, 1, 2, 3 > variable parameters into integer_ sequence<_ Ty, _ Vals...>
//Finally, integer will be returned_ sequence<size_ t, 0, 1, 2, 3>
//There is a question_ Constant didn't work.
{ // counts down to 0
};
//Right_ Make_seq uses security filtering to determine whether the number is less than 0 and equal to 0, two boundary conditions
//Automatic creation. Make a specified number of integers_ The type of sequence, such as input 3, will eventually become integer_sequence<_ Ty, 0, 1, 2, 3>
template<class _Ty,
_Ty _Size>
using make_integer_sequence = typename _Make_seq<_Size < 0, _Size == 0,
integral_constant<_Ty, _Size>, integer_sequence<_Ty> >::type;
//Create integer manually_ sequence.
template<size_t... _Vals>
using index_sequence = integer_sequence<size_t, _Vals...>;
//Create size_ Integer of type T_ Sequence, such as entering 3, will eventually become integer_sequence<size_t, 0, 1, 2, 3>
template<size_t _Size>
using make_index_sequence = make_integer_sequence<size_t, _Size>;
//You can create as many integers as you want with any number of variable parameters_ sequence<size_ t, 0... sizeof... (_Types)>
//It is called step by step
template<class... _Types>
using index_sequence_for = make_index_sequence<sizeof...(_Types)>;
2. Key analysis
1. The idea of recursively calling its own template
If you understand this, you will understand how the template recursively handles variable parameters.
template<class _Ty,
_Ty... _Vals>
struct _Make_seq<false, true,
integral_constant<_Ty, 0>,
integer_sequence<_Ty, _Vals...> >
: integer_sequence<_Ty, _Vals...>
{ // ends recursion at 0
};
template<class _Ty,
_Ty _Ix,
_Ty... _Vals>
struct _Make_seq<false, false,
integral_constant<_Ty, _Ix>,
integer_sequence<_Ty, _Vals...> >
: _Make_seq<false, _Ix == 1,
integral_constant<_Ty, _Ix - 1>,
integer_sequence<_Ty, _Ix - 1, _Vals...> >
integer_sequence<_Ty, _Ix - 1, _Vals...>
integer_ sequence<_ Ty, _ Ix - 1, _ Vals... > add the number of variable parameters + 1 (_Ix - 1)
This is why 3 becomes 1,2,3.
Let's simulate the calling process
integer_sequence<size_t, 3-1, 3>
integer_sequence<size_t, 2-1, 2, 3>
integer_ sequence<size_ t. 1-1, 1, 2, 3 > last 1 = = 1. The second parameter is true
Therefore, struct is called_ Make_ seq<false, true,integral_ constant<_ Ty, 0>
Here will be < size_ t. 0, 1, 2, 3 > variable parameters into integer_ sequence<_ Ty, _ Vals…>
Finally, integer will be returned_ sequence<size_ t, 0, 1, 2, 3>
2. integral_ The necessity of constant existence.
When you look at the above derivation process, you will find integral_ constant<_ Ty, _ IX > has always existed but has not been used. Can it be removed? With this question, we will test it
demo
#include <iostream>
#include <xtr1common>
using namespace std;
namespace xx {
template<class _Ty,
_Ty... _Vals>
struct integer_sequence
{ // sequence of integer parameters
static_assert(is_integral<_Ty>::value,
"integer_sequence<T, I...> requires T to be an integral type.");
typedef integer_sequence<_Ty, _Vals...> type;
typedef _Ty value_type;
static const size_t size()
{ // get length of parameter list
return (sizeof...(_Vals));
}
};
// ALIAS TEMPLATE make_integer_sequence
template<bool _Negative,
bool _Zero,
class _Int_seq>
struct _Make_seq
{ // explodes gracefully below 0
static_assert(!_Negative,
"make_integer_sequence<T, N> requires N to be non-negative.");
};
template<class _Ty,
_Ty... _Vals>
struct _Make_seq<false, true,
integer_sequence<_Ty, _Vals...> >
: integer_sequence<_Ty, _Vals...>
{ // ends recursion at 0
};
template<class _Ty,
_Ty _Ix,
_Ty... _Vals>
struct _Make_seq<false, false,
integer_sequence<_Ty, _Vals...> >
: _Make_seq<false, _Ix == 1,
integer_sequence<_Ty, _Ix - 1, _Vals...> >
{ // counts down to 0
};
template<class _Ty,
_Ty _Size>
using make_integer_sequence = typename _Make_seq < _Size < 0, _Size == 0,
integer_sequence<_Ty> >::type;
template<size_t... _Vals>
using index_sequence = integer_sequence<size_t, _Vals...>;
template<size_t _Size>
using make_index_sequence = make_integer_sequence<size_t, _Size>;
template<class... _Types>
using index_sequence_for = make_index_sequence<sizeof...(_Types)>;
}
int main(void)
{
index_sequence_for<int, double, float> f;
cout << typeid(decltype(f)).name() << endl;
return 0;
}
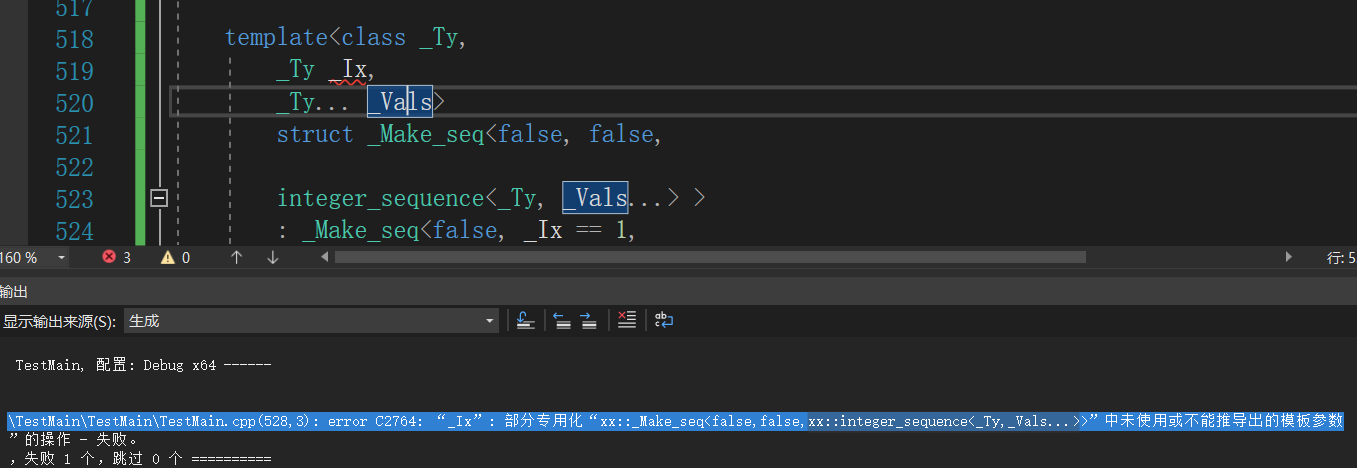
From the compilation results, it can be seen that if_ If constant is removed, it is impossible to deduce its template parameters. integer_ sequence<_ Ty, _ Ix - 1, _ Vals... > the Ix-1 here is classified as_ Vals... Here. Therefore, it is impossible to display the derived IX, so we need to use integral_constant<_ Ty, _ IX - 1 > shows one call.
summary
Learn through source code. Learn two points;
- How to use inheritance to add variable parameters.
- template<class _ Ty, _ Ty _Ix, _ Ty… _ Vals > this type needs to display the call_ Ty _ When IX is this type, use integral_constant can display the call.
Note: Here's where I'm confused. I always thought integral_ constant<_ Ty, _ IX - 1 > does not work. Think integer_ sequence<_ Ty, _ Ix - 1, _ The first variable parameter will be extracted automatically in the next recursion. template<_ Ty, __ Ix - 1,_ Vals... > but the final result is No. But careful analysis is also right. There was also an example of recursion before.
template <class _False, class _Next, class... _Rest>
struct _Disjunction<false, _False, _Next, _Rest...> { // first trait is false, try the next trait
using type = typename _Disjunction<_Next::value, _Next, _Rest...>::type;
};
template <class _False, class _Next, class... _Rest>
_Disjunction<false, _False, _Next, _Rest...>
_Disjunction<_Next::value, _Next, _Rest...>
If he really wants to use it_ Next, you need to point out the specialization.
struct _ Make_ seq<false, false,integer_ sequence<_ Ty, _ Vals... > > I don't think so. Because I wanted to use Ix, but I didn't show it. In fact, the essence is to specialize that value.
But because you can't specify a certain type, you can't specify its type, so you need to use integral_constant
I just want to use the value of Ix, but Ix cannot specify a certain type, so I use integral_constant made a transfer.
3. In the variable parameters, if you want to use the variable parameters, the first one needs to be specialized to display the call. Can only be used.