Implementation of stack and queue related algorithms

In the process of learning data structure and algorithm, in order to better understand the implementation of the algorithm, this paper implements the algorithms of stack and queue in the course. This article only provides algorithm code reference. For detailed explanation of relevant algorithms, please refer to the video course of Mr. Wang Zhuo of Qingdao University: Data and structure of Qingdao University (Wang Zhuo)

Implementation of stack

Define identifier

#include <cstdlib>
#include <iostream>
using namespace std;
// Function result status code
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define MAXSIZE 100
//Status is the type of function and its value is the result status code of the function
typedef int Status;
typedef int SElemType; // Define data element types

Chain implementation of stack

Define chain stack data structure

// Define chain stack data structure
typedef struct StackNode {
	SElemType data; // Data domain
	struct StackNode* next; // Pointer field
}StackNode,*LinkStack;

Initialize chain stack

// Initialization of chain stack
void InitStack(LinkStack& S) {
	S = NULL;
}

Judge whether the chain stack is empty

// Judge whether the chain stack is empty
Status StackEmpty(LinkStack S) {
	if (S == NULL)return TRUE;
	else return FALSE;
}

Push

// Input of chain stack
Status Push(LinkStack& S, SElemType e) {
	LinkStack p = new StackNode; // Generate new node p
	p->data = e; // Set the new node data field to e
	p->next = S; // Insert the new node into the top of the stack
	S = p; // Modify stack top pointer
	return OK;
}

Out of stack

// Out of chain stack
Status Pop(LinkStack& S, SElemType& e) {
	if (S == NULL)return ERROR;
	e = S->data;
	LinkStack p = S;
	S = S->next;
	delete p;
	return OK;
}

Access stack top element

// Get stack top element
int GetTop(LinkStack S, SElemType &e) {
	if (S != NULL) {
		e = S->data;
		return OK;
	}
	else {
		e = -2;
		return OVERFLOW;
	}
}

Test code and output results

Test code:

The input data field is [0, + ∞]. If the input data is - 1, the stack out operation will be executed.

int main()
{
	SElemType data;
	LinkStack S;
	SElemType head_data;
	int code;
	InitStack(S);
	for (int i = 0; i <= MAXSIZE; i++) {
		cout << "Merge input data elements into stack:";
		cin >> data;
		if (data == -1) { // Enter - 1 to perform the queue out operation
			Pop(S, head_data);
			cout << "Add stack top element:" << head_data << " Out of stack" << endl;
		} // if
		else {
			cout << data << " Push " << endl;
			Push(S, data);
		} // else
		code = GetTop(S, head_data);
		cout << "At this time, the top element of the stack is:" << head_data << endl;
		if (StackEmpty(S) == TRUE) {
			cout << "All data has been out of the stack" << endl;
			break;
		} // if
	} // for
	system("pause");

	return 0;
}

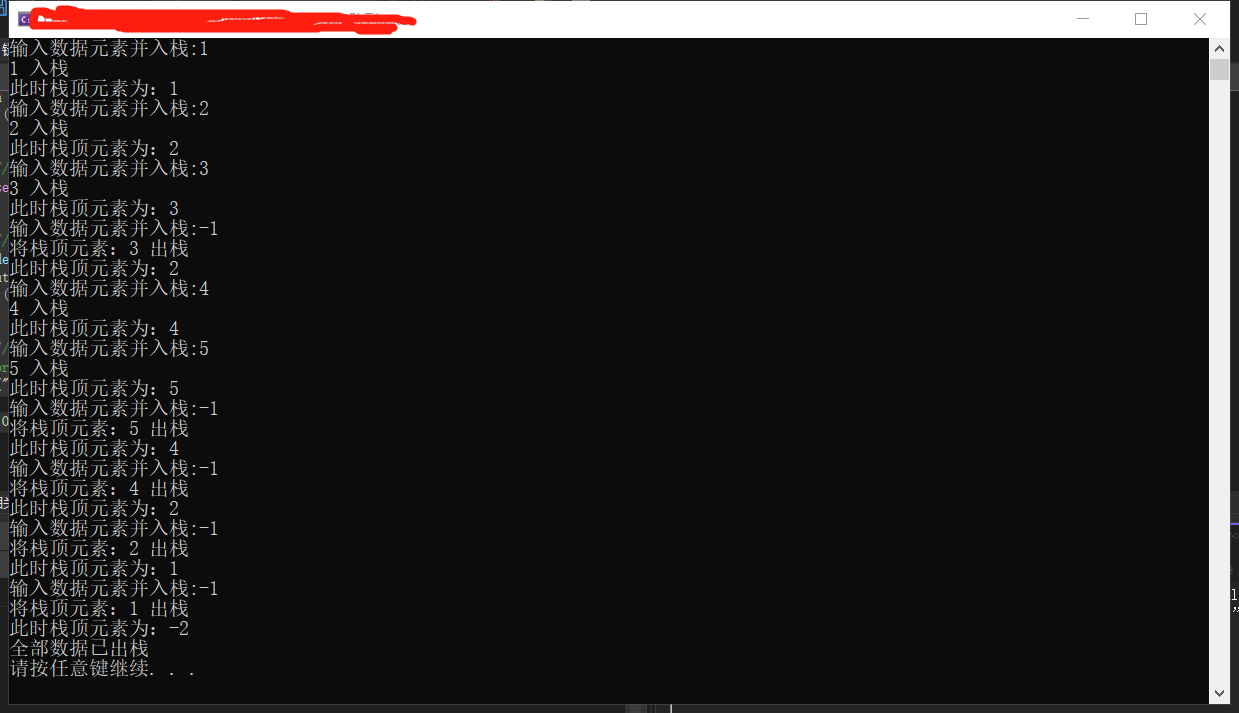
Output result:

Sequential implementation of stack

Define sequential stack data structure

typedef struct {
	SElemType *base; // Stack bottom pointer
	SElemType *top;  // Stack top pointer
	int stacksize;   // Maximum available capacity of stack
}SqStack;

Initialization sequence stack

// Initialization stack
Status InitStack(SqStack& S) { // Construct an empty stack
	S.base = new SElemType[MAXSIZE]; //or
	if (!S.base)exit(OVERFLOW); // Storage allocation failed
	S.top = S.base; // Stack top pointer equals stack bottom pointer
	S.stacksize = MAXSIZE;
	return OK;
}

Destroy sequence stack

// Destroy stack
Status DestroyStack(SqStack& S) {
	if (S.base) {
		delete S.base;
		S.stacksize = 0;
		S.base = S.top = NULL;
	}
	return OK;
}

Empty sequence stack

// Empty stack
Status ClearStack(SqStack S) {
	if (S.base)S.top = S.base;
	return OK;
}

Judge whether the sequence stack is empty

// Judge whether it is an empty stack
Status StackEmpty(SqStack S) {
	// If the stack is empty, return true; Otherwise, false is returned
	if (S.top == S.base)return TRUE;
	else return FALSE;
}

Find the length of sequential stack

// Find the length of the stack
int StackLength(SqStack S) {
	return S.top - S.base;
}

Push

// Stack operation
// Judge whether the stack is full. If it is full, an error (overflow) will be reported
// Push element e into the top of the stack
// Stack top pointer plus 1
Status Push(SqStack& S, SElemType e) {
	if (S.top - S.base == S.stacksize)return ERROR; // Stack full
	*S.top++ = e;
	return OK;
}

Out of stack

// Stack out operation
// Judge whether the stack is empty. If it is empty, there will be an error (underflow)
// Get stack top element e
// Stack top pointer minus one
Status Pop(SqStack& S, SElemType& e) {
	if (S.top == S.base)return ERROR;
	e = *--S.top;
	return OK;
}

Access order stack top element

// Get stack top element
int GetTop(SqStack S, SElemType& e) {
	if (S.top == S.base) {
		e = -2;
		return OVERFLOW;
	}
	else {
		e = *--S.top;
		return OK;
	}
}

Test code and output results

Test code:

The input data field is [0, + ∞]. If the input data is - 1, the stack out operation will be executed.

int main()
{
	SElemType data;
	SqStack S;
	SElemType head_data;
	int code;
	InitStack(S);
	for (int i = 0; i <= MAXSIZE; i++) {
		cout << "Merge input data elements into stack:";
		cin >> data;
		if (data == -1) { // Enter - 1 to perform the stack out operation
			Pop(S, head_data);
			cout << "Add stack top element:" << head_data << " Out of stack" << endl;
		} // if
		else {
			cout << data << " Push " << endl;
			Push(S, data);
		} // else
		code = GetTop(S, head_data);
		int Slen = StackLength(S);
		cout << "At this time, the stack length is:" << Slen << "\t Stack top elements are:" << head_data << endl;
		if (StackEmpty(S) == TRUE) {
			cout << "All data has been out of the stack" << endl;
			break;
		} // if
	} // for
	system("pause");

	return 0;
}

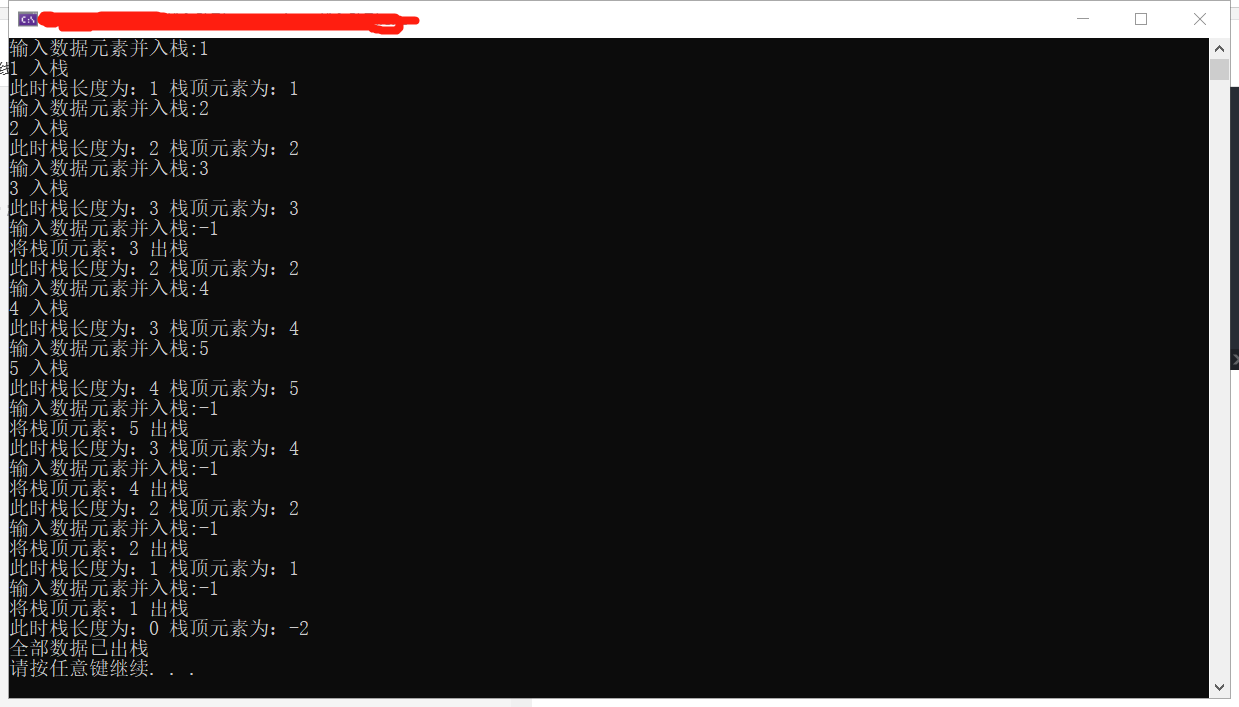
Output result:

Implementation of queue

Define identifier

#include <cstdlib>
#include <iostream>
using namespace std;
// Function result status code
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define MAXSIZE 100
#define MAXQSIZE 100 / / maximum queue length
//Status is the type of function and its value is the result status code of the function
typedef int Status;
typedef int QElemType; // Define data element types

Chain implementation of queue

Define chained queue data structure

Define data node structure

typedef struct Qnode {
	QElemType data; // Data domain
	struct Qnode* next; // Pointer field
}Qnode,*QuenePtr;

Defines the head and tail pointer of a chained queue

typedef struct {
	QuenePtr front; // Queue head pointer
	QuenePtr rear; // Tail pointer
}LinkQueue;

Initialize chained queue

// Queue initialization
Status InitQueue(LinkQueue& Q) {
	Q.front = Q.rear = new Qnode;
	if (!Q.front)exit(OVERFLOW);
	Q.front->next =NULL;
	return OK;
}

Destroy chain queue

// Queue destruction
Status DestroyQueue(LinkQueue& Q) {
	while (Q.front) {
		QuenePtr p = Q.front->next;
		delete Q.front;
		Q.front = p;
	}
	return OK;
}

Join the team

// Queue up
Status EnQueue(LinkQueue& Q, QElemType e) {
	QuenePtr p = new Qnode;
	if (!p)exit(OVERFLOW);
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	return OK;
}

Out of the team

// Queue out
Status DeQueue(LinkQueue& Q, QElemType& e) {
	if (Q.front == Q.rear)return ERROR;
	QuenePtr p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if (Q.rear == p)Q.rear = Q.front;
	delete p;
	return OK;
}

Access queue header element

// Queue header element
Status GetHead(LinkQueue Q,QElemType &e) {
	if (Q.front == Q.rear) {
		return OVERFLOW;
	}// if
	else {
		e = Q.front->next->data;
		return OK;
	}
}

Test code and output structure

Test code:

The input data field is [0, + ∞]. If the input data is - 1, the stack out operation will be executed.

int main()
{
	QElemType data;
	LinkQueue Q;
	QElemType head_data;
	int code;
	InitQueue(Q);
	for (int i = 0; i <= MAXQSIZE; i++) {
		cout << "Enter data elements and join the team:";
		cin >> data;
		if (data == -1) { // Enter - 1 to perform the queue out operation
			DeQueue(Q, head_data);
			cout << "Add team leader element:" << head_data << " Out of the team" << endl;
		} // if
		else {
			cout << data << " Join the team" << endl;
			EnQueue(Q, data);
		} // else
		code = GetHead(Q, head_data);
		cout <<"\t The team head elements are:" << head_data << endl;
		if (code == -2) {
			cout << "All data out of the queue,Perform the destroy queue operation" << endl;
			DestroyQueue(Q);
			cout << "Queue destroyed" << endl;
			break;
		} // if
	} // for
	system("pause");

	return 0;
} // main

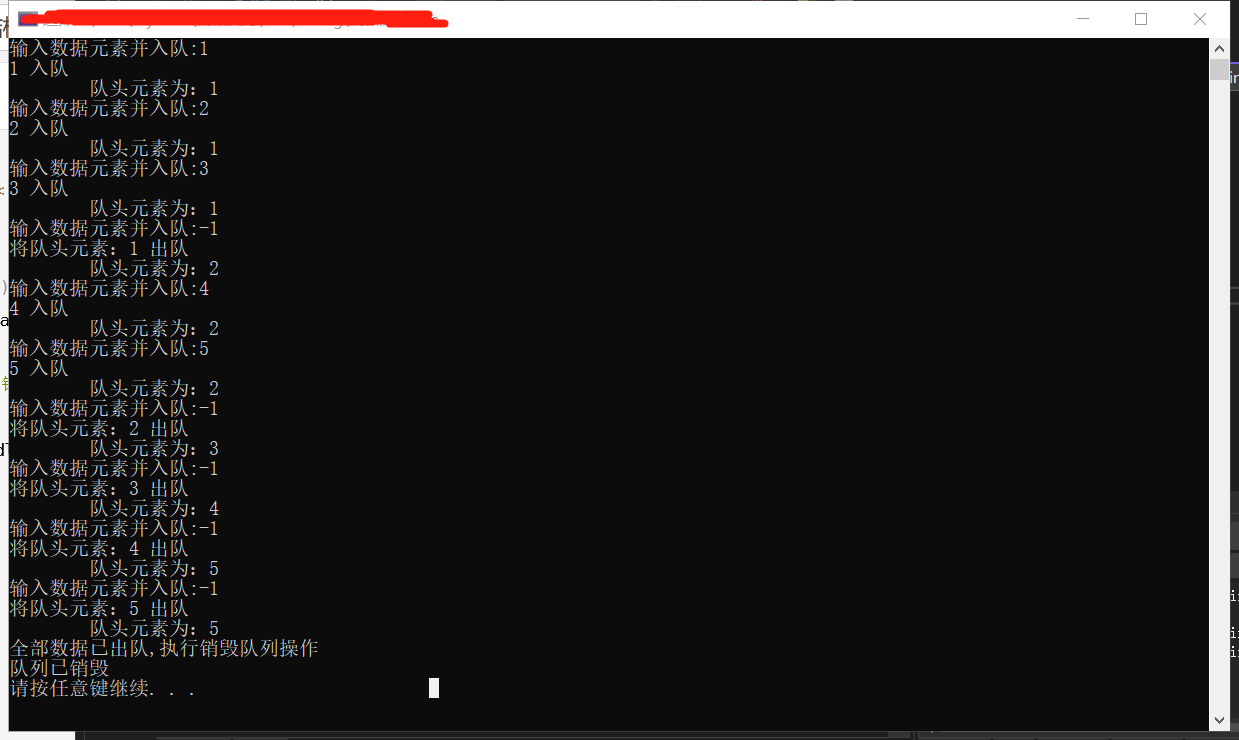
Output result:

Sequential implementation of queue

Define sequential queue data structure (circular queue)

// Define sequential queue data structure
typedef struct {
	QElemType* base; //Initialize dynamic allocation of sequential space
	int front; // Head pointer
	int rear;  // Tail pointer
}SqQueue;

Initialize sequential queue

// Queue initialization
Status InitQueue(SqQueue& Q) {
	Q.base = new QElemType[MAXQSIZE]; // Allocate array space
	if (!Q.base)exit(OVERFLOW); // memory allocation failed
	Q.front = Q.rear = 0; // The head pointer and tail pointer are set to 0 and the queue is empty
	return OK;
}

Get sequence queue length

// Find the length of the queue
int QueueLength(SqQueue Q) {
	return ((Q.rear - Q.front + MAXQSIZE) % MAXQSIZE);
}

Queue up (circular queue)

// Queue up of circular queue
Status EnQueue(SqQueue& Q, QElemType e) {
	if ((Q.rear + 1) % MAXQSIZE == Q.front)return ERROR; // Team full
	Q.base[Q.rear] = e; // New elements added to the tail of the team
	Q.rear = (Q.rear + 1) % MAXQSIZE; // Tail pointer + 1
	return OK;
}

Out of line (circular queue)

// Out of queue of circular queue
Status DeQueue(SqQueue& Q, QElemType& e) {
	if (Q.front == Q.rear)return ERROR; // Team air
	e = Q.base[Q.front];  // Save queue header element
	Q.front = (Q.front + 1) % MAXQSIZE; // Team leader pointer + 1
	return OK;
}

Access queue header element

// Take the team head element
Status GetHead(SqQueue Q) {
	if (Q.front != Q.rear) {
		return Q.base[Q.front]; // Return queue header element
	}
	else {
		return OVERFLOW; // Return error code
	}
}

Test code and output structure

Test code:

The input data field is [0, + ∞]. If the input data is - 1, the stack out operation will be executed.

int main()
{
	QElemType data;
	SqQueue Q;
	QElemType head_data;
	InitQueue(Q);
	for (int i = 0; i <= MAXQSIZE; i++) {
		cout << "Enter data elements and join the team:";
		cin >> data;
		if (data == -1) { // Enter - 1 to perform the queue out operation
			DeQueue(Q, head_data);
			cout << "Add team leader element:" << head_data << " Out of the team" << endl;
		} // if
		else {
			cout << data << " Join the team" << endl;
			EnQueue(Q, data);
		} // else
		int Qlen = QueueLength(Q);
		head_data = GetHead(Q);
		cout << "At this time, the queue length is:" << Qlen << "\t The team head elements are:" << head_data << endl;
		if (QueueLength(Q) == 0) {
			cout << "All data are out of the queue" << endl;
			break;
		} // if
	} // for
	system("pause");

	return 0;
} // main

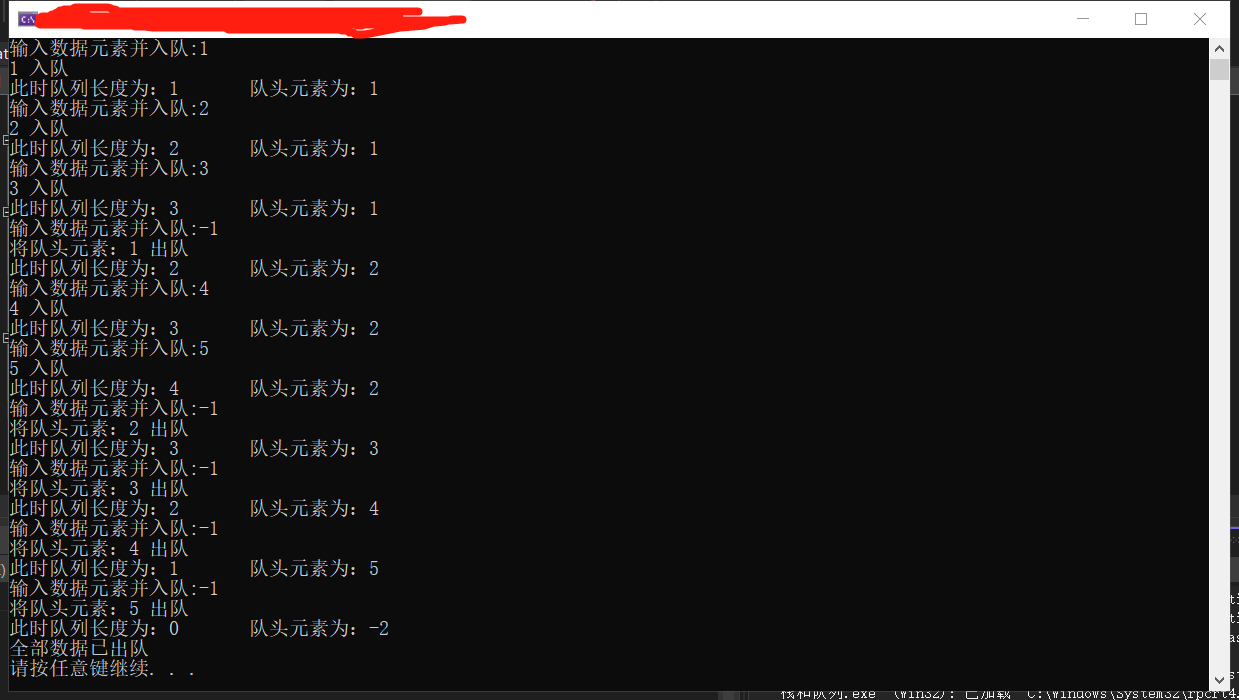
Output result: