The basic graph theory algorithms are summarized here: Summary of basic graph theory algorithms (shortest path, minimum spanning tree, bipartite graph)

LCA

Upward marking method

Time complexity O ( n ∗ m ) O(n*m) O(n∗m)

If the two nodes are different, move the deeper node upward until it moves to the same node, then the node is the common ancestor node.

code

//Preprocess the depth of each node and the number of the parent node of the node
void dfs(int u, int father){
    depth[u]=depth[father]+1;
    fa[u]=father;

    for(int i=h[u];~i;i=ne[i]){
        int v=e[i];
        if(v!=father) dfs(v,u);
    }
}
//Common ancestor of u and v
int getlca(int u,int v){
    //As long as u and v are different
    while(u!=v){
        //Move the node with large depth upward
        if(depth[u]<depth[v]) v=fa[v];
        else u=fa[u];
    }
    return u;
}

Multiplication method

Pretreatment O ( n l o g n ) O(nlogn) O(nlogn)

• f a [ i ] [ j ] fa[i][j] fa[i][j] indicates the slave node i i i start, go up 2 j 2^j The number of the node in step 2j. If the root node has been exceeded, f a [ i ] [ k ] = 0 fa[i][k]=0 fa[i][k]=0. In particular, f a [ i ] [ 0 ] fa[i][0] fa[i][0] is i i The root node of i.

• d e p t h [ i ] depth[i] depth[i] indicates depth. The depth of the root node is 1, i.e d e p t h [ r o o t ] = 1 depth[root]=1 depth[root]=1.

• Sentry: if from i i i start jumping 2 j 2^j Step 2j will skip the root node, then f a [ i ] [ j ] = 0 fa[i][j]=0 fa[i][j]=0. d e p t h [ 0 ] = 0 depth[0]=0 depth[0]=0

• Recurrence relation: f a [ i ] [ k ] = f a [ f a [ i ] [ k − 1 ] ] [ k − 1 ] fa[i][k]=fa[fa[i][k-1]][k-1] fa[i][k]=fa[fa[i][k−1]][k−1]

inquiry O ( l o g n ) O(logn) O(logn)

1. Jump the two points to the same floor first
2. Let the two points jump up at the same time until the next level of their nearest common ancestor

code

int ne[maxn],e[maxn],h[maxn],idx;
int fa[maxn][21],dep[maxn];
int root;
void bfs(){
    queue<int>q;
    q.push(root);
    dep[root]=1,dep[0]=0;
    // Sentry depth[0] = 0: if you skip 2^j steps from i, you will skip the root node 
    // fa[fa[j][k-1]][k-1] = 0
    // Then Fa [i] [J] = 0 dep [Fa [i] [J] = dep [0] = 0
    while(q.size()){
        int t=q.front(); q.pop();
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(dep[j]) continue;
            dep[j]=dep[t]+1;
            q.push(j);
            fa[j][0]=t;
            for(int k=1;k<=18;k++){ //Pay attention to the boundary
                fa[j][k]=fa[fa[j][k-1]][k-1];
            }
             /*
            For example, understand how to exceed the root node
            Because we do not assign a value to the root node fa[1][0], then fa[1][0] = 0;
                 1
                / \
               2   3 
            fa[1][0] = 0;
            fa[2][0] = 1;
            fa[2][1] = fa[fa[2][0]][0] = fa[1][0] = 0;
            */
        }
    }
}

int lca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(int k=18;k>=0;k--)
        if(dep[fa[x][k]]>=dep[y])
            x=fa[x][k];
    
    if(x==y) return x;
    for(int k=18;k>=0;k--){
        if(fa[x][k]!=fa[y][k]){
            x=fa[x][k];
            y=fa[y][k];
        }
    }

    return fa[x][0];
}

Tarjan

Time complexity O ( n + m ) O(n+m) O(n+m), offline approach

thinking

In depth first traversal, nodes are divided into three categories:

1. Branch being searched
2. It has been traversed and traced back
3. Points not yet searched

When we draw a graph, we can find that the first kind of points are like fruits hanging on a certain point. When we enumerate one point, the other point is the first kind of point, and their nearest common ancestor is the point hanging on the first kind of point

So we can search. If the marked point is the first kind of point in the search process, we can enumerate the queries about this point when tracing back. If the other point is the first kind of point, we can get the nearest common ancestor of this group of queries

If the other point is not the first type of point, it will be ignored temporarily, because our point will soon become the first type of point. At that time, we will take that point to complete the calculation of this group of queries. Finally, we will merge the current point into the parent node, and then the current point will become the second type of point. Finally, we can output it uniformly to complete the offline solution of the nearest public ancestor

code

/*
In depth first traversal, all points are divided into three categories:
[0] Points not yet searched
[1] Branch being searched
[2] It has been traversed and traced back
*/
void tarjan(int u){
    st[u]=1;
    // u the lower left point of the root node on this road is used to query the set and to the root node
    for(int i=h[u];~i;i=ne[i]){
        int j=e[i];
        if(st[j]) continue;
        tarjan(j);
        p[j]=u; //After backtracking from the lower left, merge the lower left points to the root node
    }

    // For the current point u, search all queries to see whether the results can be obtained
    for(auto item:ask[u]){
        int y=item.first,id=item.second;
        if(st[y]==2){ //This point has been backtracked, that is, it has been merged with the query set
            int anc=find(y);
            ans[id]=dis[u]+dis[y]-dis[anc]*2; //Keep the original order output
        }
    }
    st[u]=2; //When the point u has been searched and needs to be traced back, mark st[u] as 2 
}

Strongly connected component SCC of digraph

Strongly connected graph: given a directed graph. If there is a path from X to y and a path from y to X for any two nodes x, y in the graph, the directed graph is called "strongly connected graph".

Strongly connected component (SCC) refers to the polar connected subgraph of a strongly connected graph (with the most points).

In human words, any two points in a strongly connected component have edges. If any other point is added, it will no longer be a connected component.

In other words, for a directed graph, the strongly connected component is the graph with any two points having a path (x can reach y, y can also reach x) and containing the most points.

What is the use of strongly connected components of digraphs?

It mainly transforms a directed graph into a directed acyclic graph (topological graph, DAG) by reducing the point (reducing the strongly connected component to a point).

Tarjan

purpose

• Contraction point of a directed graph (directed graph - > directed acyclic graph)

Algorithm idea

1. Add time stamp and initialize i, j marks;
2. Put it into the stack and mark it;
3. Ergodic neighbor
   1. If you haven't traversed it, tarjan again and update the minimum value low with low[j]
   2. If it is on the stack, update the minimum value low with dfn[j]
4. Find the highest point
   1. Number of scc++
   2. Do while loop:
      Take each element out of the stack; The sign is out of stack;
      Which scc does the element belong to; Number of points in this scc++

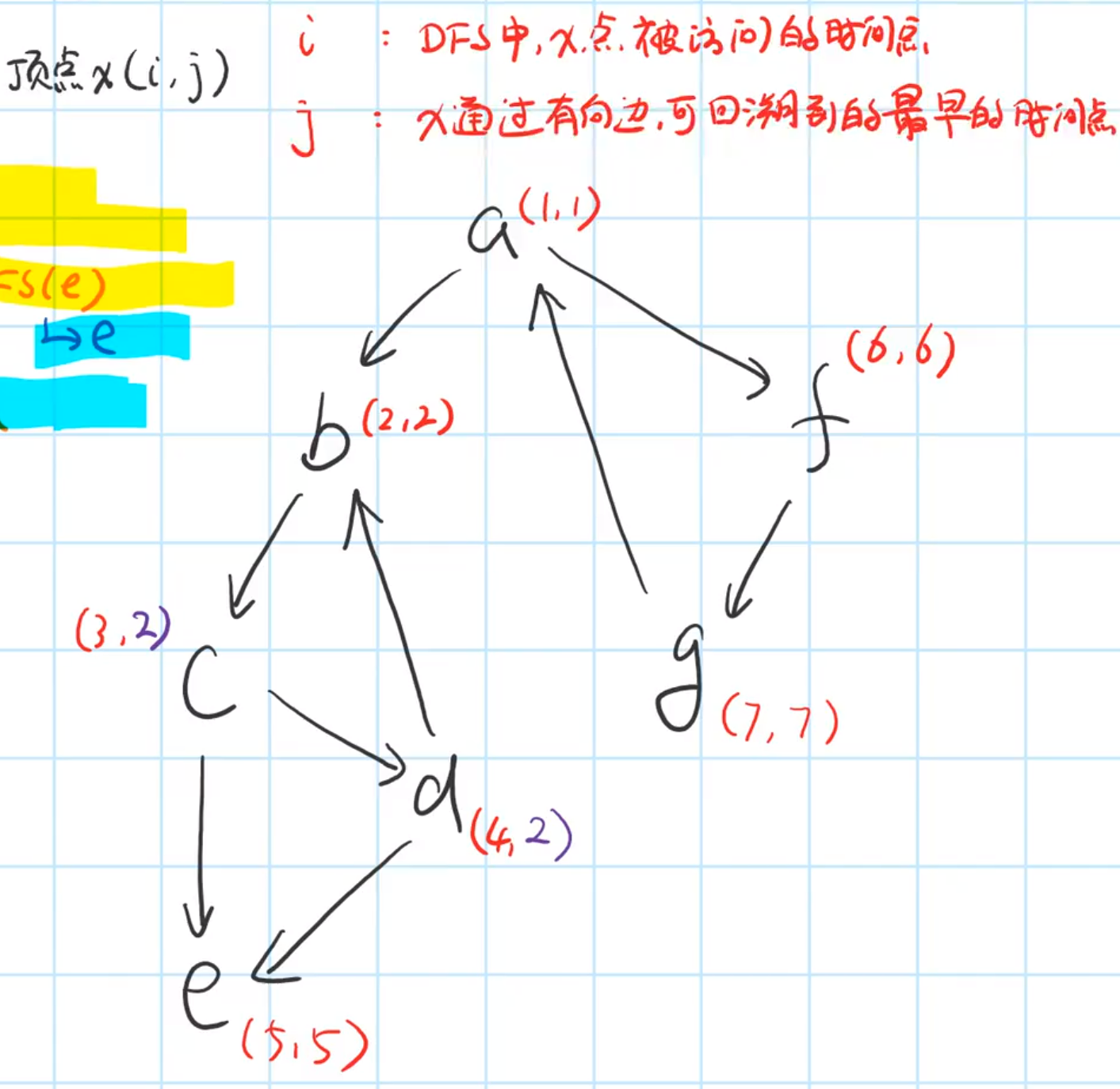
Template

// tarjan algorithm for strongly connected components
// Time complexity O(n+ m)
void tarjan(int u){
    // Initialize your own timestamp
    dfn[u] = low[u] = ++ timestamp;
    //Put the point on the stack
    stk[++ top] = u, in_stk[u] = true;
    // Traversing points connected with u
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(!dfn[j]){//If it has not been traversed, low[j] must have a value at this time
            tarjan(j);
            // The minimum value of the timestamp that the update u can traverse
            low[u] = min(low[u], low[j]);
        }
        // If the current point is in the stack
        // Note that the points stored in the stack may be several different branches of the tree, because there are cross edges
        // All the points stored in the stack are the points that have not been searched, and they are not the highest point of the strongly connected component
        // This indicates that the current strongly connected component has not been traversed, that is, there is a value in the stack
        else if(in_stk[j])
            //Update the minimum time stamp that u points can reach
            //At this time, j is either the ancestor of u or the point of the cross edge, and the timestamp is less than u
            low[u] = min(low[u], dfn[j]);
    }
    // Find the highest point of the connected component
    if(dfn[u] == low[u]){
        int y;
        ++ scc_cnt; // Number of strongly connected components++
        do{// Take out all points of the connected component
            y = stk[top --];
            in_stk[y] = false;
            id[y] = scc_cnt; // Which connected component does the marked point belong to
            size_scc[scc_cnt] ++;
        } while(y != u);
    }
}

Examples

AcWing 1174. Popular cattle

#include<bits/stdc++.h>
using namespace std;

const int N = 10010, M = 50010;

int n, m;
int h[N], w[M], e[M], ne[M], idx; // A set of adjacency table
// dfn[u] stores the timestamp of traversal to u
// low[u] stores the smallest timestamp that can be traversed by traversing the subtree from U
//Timestamp is the timestamp
int dfn[N], low[N], timestamp;
int stk[N], top; // Stack, and stack top element index
bool in_stk[N]; // Is it on the stack
//id[u] indicates the number of strongly connected components of u, scc_cnt represents the number of strongly connected components
// size_scc[u] indicates the number of midpoint of strong connected component numbered U
int id[N], scc_cnt, size_scc[N];
int dout[N];// Record the degree of each point in the new graph (that is, each connected component of the original graph)

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void tarjan(int u){
    //Timestamp of the current point
    dfn[u] = low[u] = ++ timestamp;
    // Add to stack
    stk[++ top] = u, in_stk[u] = true;
    
    //Traverse all adjacent points of u point
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(!dfn[j]){//If not traversed
            tarjan(j); // Traverse it
            low[u] = min(low[u], low[j]);
        }
        // The current point is in the stack
        else if(in_stk[j]) low[u] = min(low[u], dfn[j]);
    }
    
    if(dfn[u] == low[u]){
        ++ scc_cnt; // Update the number of strongly connected components
        int y;
        do{
            y = stk[ top--]; //Constantly take out the elements in the stack
            in_stk[y] = false;
            id[y] = scc_cnt; //Number of connected block to which the y element belongs
            size_scc[scc_cnt] ++; //The number of points contained in the connected block
        }while(y != u); // Until y is not equal to u
    }
    
}

int main(){
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while(m --){
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    
    for(int i = 1; i <= n; i ++){
        if(!dfn[i])
            tarjan(i);
    }
    
    // Directed acyclic graph
    // Count the outgoing degree of all points in the new graph
    for(int i = 1; i <= n; i ++){
        for(int j = h[i]; ~j; j = ne[j]){
            int k = e[j];
            int a = id[i]; //a represents the number of the connected component where i is located
            int b = id[k]; // b represents the number of the connected component where k is located
            //If point i and point k are not in the same connected block
            // dout saves the degree, because this problem only needs the degree
            //In other topics, it may be to build edges, because here is to construct directed acyclic graphs
            if(a != b) dout[a] ++; // From a to b, the exit of A++
        }
    }
    
    // Relevant parts of this topic:
    // zeros is the number of points with a degree of 0 in the new graph
    // sum indicates the number of points (the most popular cows) that meet the conditions
    int zeros = 0, sum = 0;
    for(int i = 1; i <= scc_cnt; i ++){
        if(!dout[i]){
            zeros ++;
            sum += size_scc[i];
            if(zeros > 1){
                sum = 0;
                break;
            }
        }
    }
    cout << sum << endl;
}

Some conclusions

• After shrinking point, there is i i i starting points j j j end points, and then add m a x ( i , j ) max(i,j) max(i,j) edges, which can become strongly connected.

Double connected component DCC of undirected graph

classification

• Side double connected component e-DCC
  • Maximal connected block without bridge
• Two point connected component v-DCC
  • Maximal connected block without cut point

Shrink to a tree

Algorithm idea

Code edge

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 5010, M = 20010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
int id[N], dcc_cnt;
bool is_bridge[M];
int d[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void tarjan(int u, int from)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if (dfn[u] < low[j])
                is_bridge[i] = is_bridge[i ^ 1] = true;
        }
        else if (i != (from ^ 1))
            low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u])
    {
        ++ dcc_cnt;
        int y;
        do {
            y = stk[top -- ];
            id[y] = dcc_cnt;
        } while (y != u);
    }
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    tarjan(1, -1);

    for (int i = 0; i < idx; i ++ )
        if (is_bridge[i])
            d[id[e[i]]] ++ ;

    int cnt = 0;
    for (int i = 1; i <= dcc_cnt; i ++ )
        if (d[i] == 1)
            cnt ++ ;

    printf("%d\n", (cnt + 1) / 2);

    return 0;
}

Code point

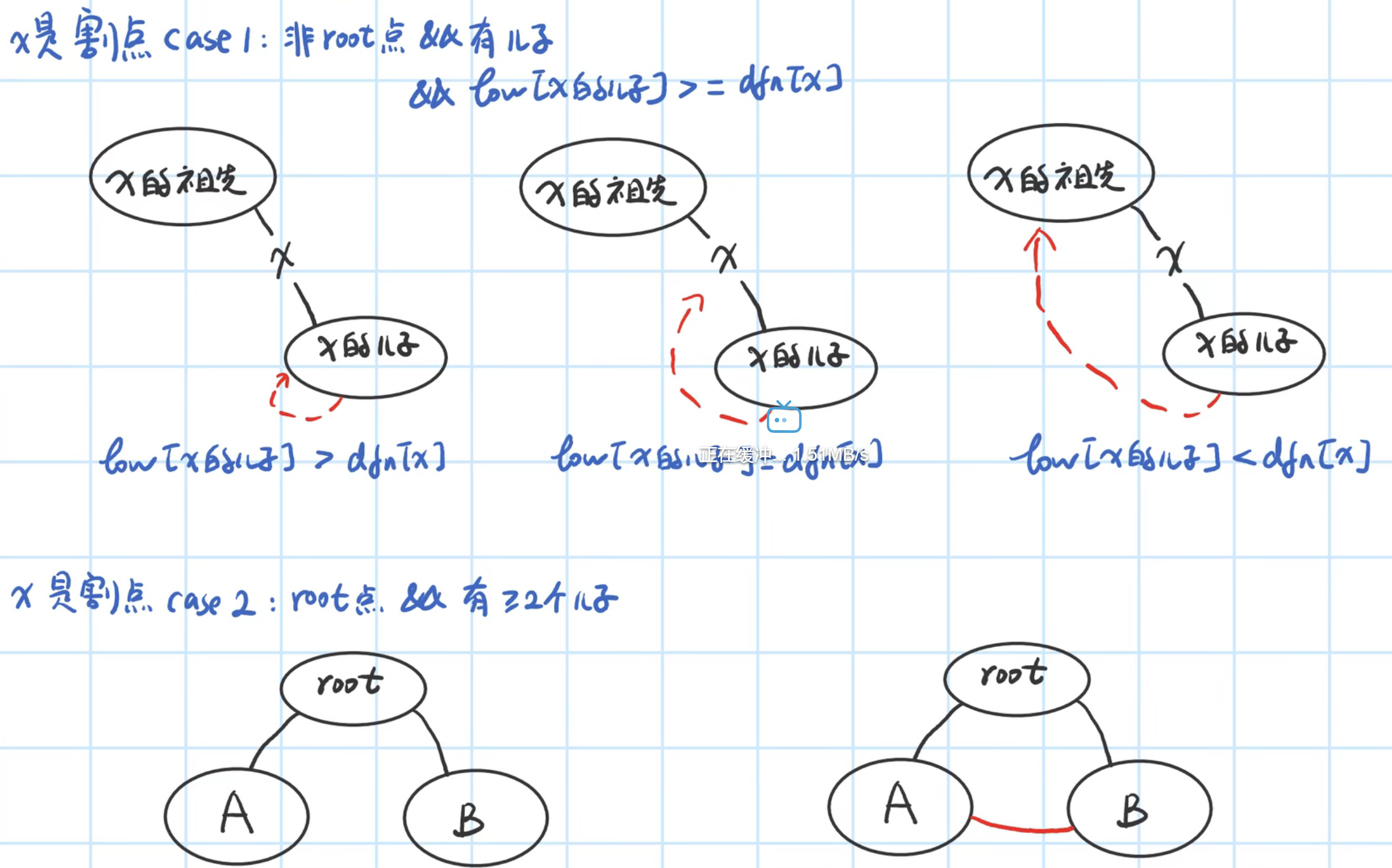
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010, M = 30010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int root, ans;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;

    int cnt = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
            if (low[j] >= dfn[u]) cnt ++ ;
        }
        else low[u] = min(low[u], dfn[j]);
    }

    if (u != root) cnt ++ ;

    ans = max(ans, cnt);
}

int main()
{
    while (scanf("%d%d", &n, &m), n || m)
    {
        memset(dfn, 0, sizeof dfn);
        memset(h, -1, sizeof h);
        idx = timestamp = 0;

        while (m -- )
        {
            int a, b;
            scanf("%d%d", &a, &b);
            add(a, b), add(b, a);
        }

        ans = 0;
        int cnt = 0;
        for (root = 0; root < n; root ++ )
            if (!dfn[root])
            {
                cnt ++ ;
                tarjan(root);
            }

        printf("%d\n", ans + cnt - 1);
    }

    return 0;
}

Some conclusions

• After shrinking, a tree is formed, and the tree has c n t cnt cnt leaf nodes, add ⌊ c n t + 1 2 ⌋ \lfloor \frac{cnt+1}{2 }\rfloor ⌊ 2cnt+1 ⌋ edges, which can make it doubly connected.

Euler path and Euler loop

Euler path: for graph G, if there is a path containing all edges in G, the path becomes an Euler path, also known as Euler path.

Euler loop: if the Euler path is a loop (you can return from the starting point to the ending point), it is called Euler loop.

Euler graph: a graph containing an Euler loop is an Euler graph.

determine

• Directed graph
  • Euler path: the number of all singularity points in the graph is 0 or 2.
  • Euler loop: the degrees of all points in the diagram are even.
• Undirected graph
  • Euler path: the penetration of all points is equal to the exit, or there is one point where the exit is 1 greater than the penetration (starting point), one point where the penetration is 1 greater than the exit (end point), and the penetration of other points is equal to the exit.
  • Euler loop: the in degree of all points is equal to the out degree.

thinking

skill

Edge transformation

The sequence number of edges in undirected graph is: 0 ∼ 2 m − 1 0\sim2m-1 0 ∼ 2m − 1, and the number in the title is 1 ∼ m 1\sim m 1∼m;

Therefore, when transforming edges: 0,1 corresponds to edge 1, 2,3 corresponds to edge 2, that is, edge x corresponds to x/2+1

The even number is the positive edge and the odd number is the reverse edge. The relationship between the positive and reverse edges can be transformed by x^1;

If it is an odd number: in x^1, the number in front of X binary remains unchanged, and the last bit becomes 0, that is, x^1 =x-1;

If it is an even number: in x^1, the number in front of X binary remains unchanged, and the last bit becomes 1, that is, x^1=x+1;

Search optimization

code: Decision Euler circuit

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100100, M = 400100;

int h[N],e[M],ne[M],idx;
int ans[N*2],cnt;
bool used[M];
int din[N],dout[N];
int n,m,ver;

void add(int a,int b){
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

void dfs(int u){
    for(int &i = h[u]; ~i; ){
        if(used[i]){  //If this edge is used
            i = ne[i];   //Delete this edge
            continue;
        }

        used[i] = true;  //Mark this edge as used
        if(ver == 1) used[i^1] = true;   //If it is an undirected graph, the reverse edge of this edge should also be marked

        int t;
        if(ver == 1){
            t = i/2 + 1;
            if(i&1) t = -t;  //(0,1) (2,3) (4,5) odd numbers are returned edges

        }else t = i+1;

        int j = e[i];
        i = ne[i];
        dfs(j);
        ans[cnt++] = t;
    }
}
int main()
{
    scanf("%d%d%d",&ver,&n,&m);
    memset(h,-1,sizeof h);

    for(int i = 0; i<m; i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        if(ver == 1) add(b,a);  //Undirected edge
        din[b]++, dout[a]++;   
    }

    if(ver == 1){
        for(int i = 1; i<=n; i++){
            if(din[i]+dout[i] &1){
                //The necessary and sufficient condition for an undirected graph to contain an Euler circuit is that the degree of each point is even
                puts("NO");
                return 0;
            }
        }
    }else{
        for(int i = 1; i<=n; i++){
            if(din[i] != dout[i]){
                //The necessary and sufficient condition for a directed graph to contain Euler circuits is that the in degree of each point is equal to the out degree
                puts("NO");
                return 0;
            }
        }
    }

    for(int i = 1; i<=n; i++){
        if(~h[i]) {
            dfs(i);
            break;
        }
    }

    if(cnt < m){
        puts("NO");
        return 0;
    }

    puts("YES");
    for(int i = cnt-1; i>=0; --i){
        cout<<ans[i]<<" ";
    }
    return 0;
}

Topological sorting

purpose

• Topological sorting can determine whether there are rings in A directed graph. We can perform the above process on any directed graph and check the length of A sequence after completion. If the length of A sequence is less than the number of points in the graph, it indicates that some nodes are not traversed, and then it indicates that there are rings in the graph.
• Find topological order

thinking

Continuously select the point x with the penetration of 0, and the penetration of the point connecting x to - 1.

code

void topsort(){
    for(int i=1;i<=n;i++)
        if(!din[i])
            q.push(i);
    
    while(q.size()){
        int t=q.front(); q.pop();
        ans[++cnt]=t;
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            din[j]--;
            if(din[j]==0) q.push(j);
        }
    }
}

01 planning

Use

In graph theory problems, the following forms appear:
∑ f ( i ) ∑ t ( i ) of most large value \Maximum value of frac{\sum f(i)}{\sum t(i)} Maximum value of Σ t(i) ∑ f(i)
Consider using 01 planning

thinking

code

#include <bits/stdc++.h>
#define endl "\n"
#define debug(x) cout << #x << ": -----> " << x << endl;
using namespace std;

const int maxn=5e5+10;
int e[maxn],ne[maxn],h[maxn],idx,wp[maxn],wseg[maxn];
double dis[maxn];
int cnt[maxn];
bool st[maxn];
int L,P;

void add(int a,int b,int c){
    e[idx]=b,wseg[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

bool spfa(double mid){
    memset(st,0,sizeof st);
    memset(cnt,0,sizeof cnt);
    queue<int> q;
    for(int i=1;i<=L;i++){
        q.push(i);
        st[i]=true;
    }
    while(q.size()){
        int t=q.front(); q.pop(); st[t]=false;
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            // double v=j*mid
            if(dis[j]<dis[t]+wp[t]-mid*wseg[i]){
                dis[j]=dis[t]+wp[t]-mid*wseg[i];
                cnt[j]=cnt[t]+1;

                if(cnt[j]>=L) return true;

                if(!st[j]){
                    st[j]=true;
                    q.push(j);
                }
            }
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin>>L>>P;
    for(int i=1;i<=L;i++) cin>>wp[i];

    memset(h,-1,sizeof h);
    for(int i=1;i<=P;i++){
        int a,b,c; cin>>a>>b>>c;
        add(a,b,c);
    }

    double l=0,r=1e7;
    while(r-l>1e-4){
        double mid=(l+r)/2;
        if(spfa(mid)) l=mid;
        else r=mid;
    }

    cout<<fixed<<setprecision(2)<<l;
    return 0;
}

Differential constraint

Bipartite graph

Floyd