Title: give you two strings, haystack and need. Please find the first position of the need string in the haystack string (the subscript starts from 0). If it does not exist, - 1 is returned. 0 is returned when {need} is an empty string.
leetcode: https://leetcode-cn.com/problems/implement-strstr/
Premise of problem solution
This question means to find the position of the string to be matched in a string. If it does not exist, it returns - 1.
We call this string the original string and the string to be matched the pattern string.
Naive algorithm (violence)
The intuitive solution is to enumerate each character in the original string {string as the "starting point", and try to match each time from the "starting point" of the original string and the "first place" of the matching string:
- Matching succeeded: return the "starting point" of the original string of this matching
- Matching failed: enumerate the next "starting point" of the original string and try matching again.
code:
public class Solution {
public int strStr(String string, String pattern) {
if (pattern == null || pattern.length() == 0) {
return 0;
}
for (int i = 0; i <= string.length() - pattern.length(); i++) {
if (string.charAt(i) != pattern.charAt(0)) {
continue;
}
int pidx = 0;
for (; pidx < pattern.length(); pidx++) {
if (string.charAt(i + pidx) != pattern.charAt(pidx)) {
break;
}
}
if (pidx == pattern.length()) {
return i;
}
}
return -1;
}
}Code optimization
In fact, this algorithm can be optimized. For example, during the matching process, record the next starting position in the matched characters. If this match fails, proceed with the following logic
- The next starting position exists: start the next matching directly from this position
- There is no match in the starting point of the string: start directly from the starting point of the next failure
So how do you define where this next start is?
The next start position is actually: remove the current "starting point", the first character that appears the same as the first character of the mode string. (because the condition for entering the matching process is that the character of "starting point" is the same as the first character of the pattern string)
Conflict situations
- The "starting point" conflicts with the first character of the mode string
- The string of the "starting point" conflicts with the pattern string, but among the characters matched by the original string, there are characters that are the same as the first character of the pattern string after removing the "starting point".
- The string of the "starting point" conflicts with the pattern string, but among the characters matched by the original string, there is no character that is the same as the first character of the pattern string after removing the "starting point"
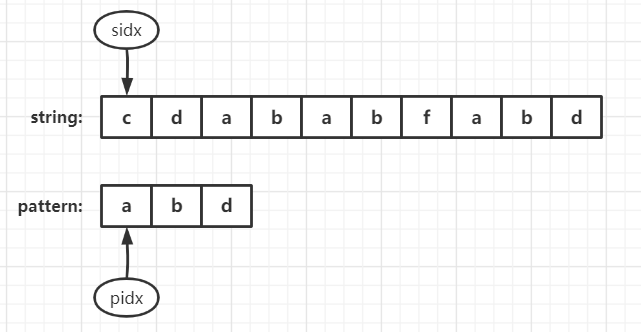
First case
In this case, start matching directly from sidx+1
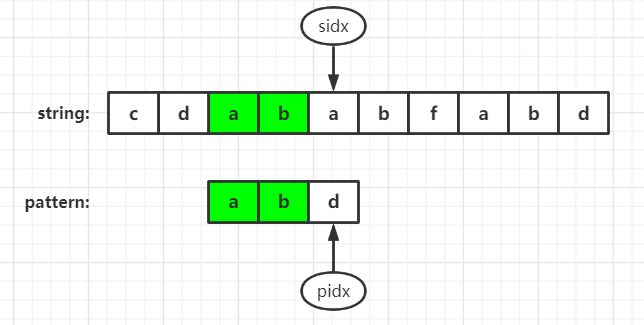
The second case
Since sidx is the same as the first character of the pattern string and sidx is the first character that is the same as the first character of the pattern string after removing the "starting point", next = sidx at this time and the next matching starts from next
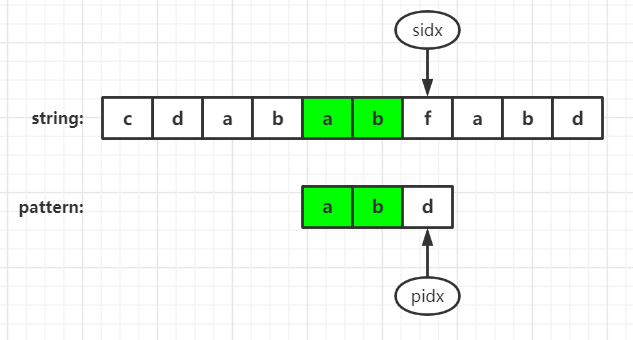
The third case
In this case, next = -1. Just restart the matching from sidx+1
public class Solution {
public int strStr(String string, String pattern) {
if (pattern == null || pattern.length() == 0) {
return 0;
}
int next = -1;
int sidx = 0;
int pidx = 0;
// Length of starting point
// For example, string = "abcabd", pattern = "abd"
// Then the starting point can be the first four characters of "abca", so the length of the starting point can be calculated in this way
int startLen = string.length() - pattern.length() + 1;
// sidx - pidx = origin index
while (sidx - pidx < startLen) {
/*
* Judge whether it is the starting point. If it is the starting point, skip the next update directly, otherwise enter the next step to judge
* Judge whether the next starting point has been found. If next == -1 indicates that the starting point has not been found, otherwise it has been found. If not, proceed to the next step of judgment
* Judge whether the current character of the original string is the same as the first character of the mode string. If it is the same, it indicates that the change point is the next starting point
*/
if (pidx != 0 && next == -1 && string.charAt(sidx) == pattern.charAt(0)) {
next = sidx;
}
if (string.charAt(sidx) == pattern.charAt(pidx)) {
sidx++;
pidx++;
if (pidx == pattern.length()) {
return sidx - pattern.length();
}
} else {
if (next != -1) {
sidx = next;
next = -1;
} else {
sidx++;
}
pidx = 0;
}
}
return -1;
}
}
KMP algorithm
KMP algorithm is studied by three people. KMP is the initials of these three people's names.
1. Matching process
for instance
Original string: "abcabdabcabf"
Mode string: "abcabf"
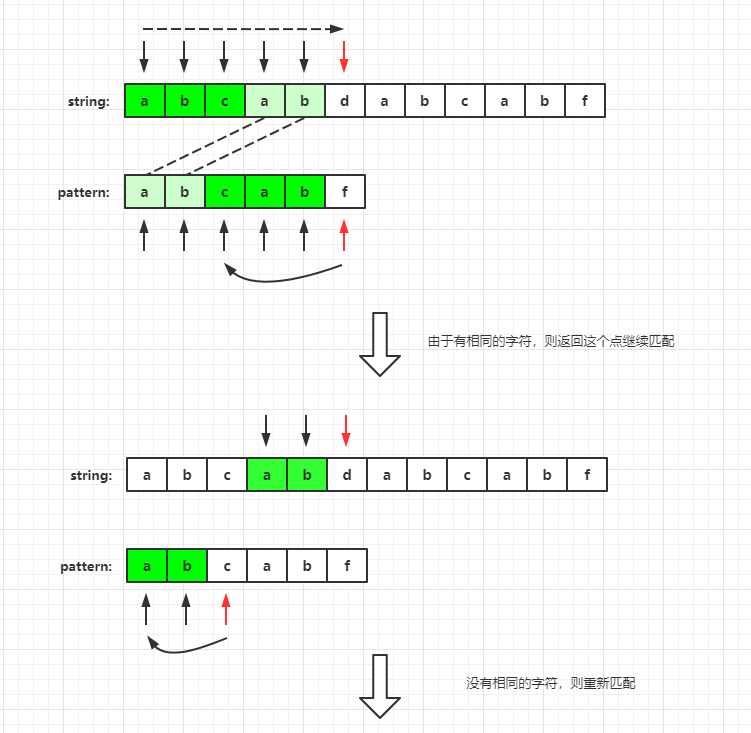
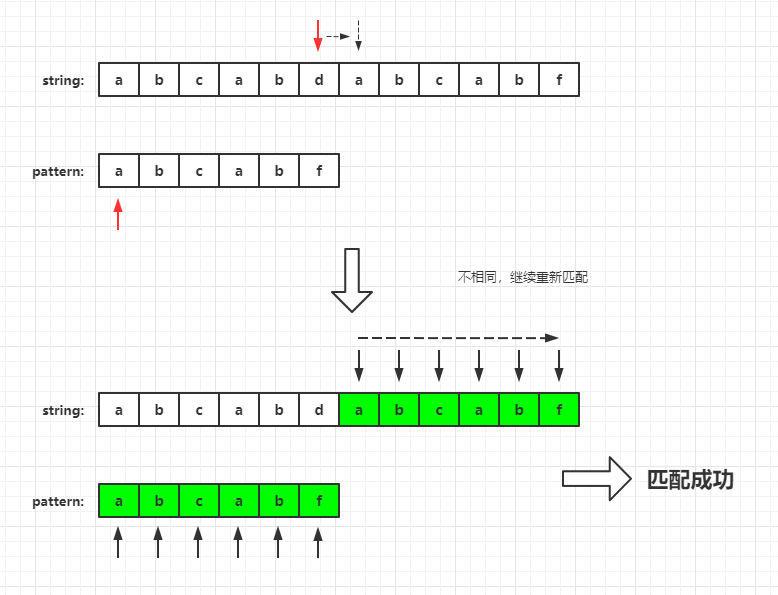
This is the matching process of KMP algorithm. Let's look at the principle of KMP.
2. Prefix table
To clarify the KMP algorithm, the most important thing is to clarify the prefix and suffix and how to generate the prefix table. The prefix table is used for fallback. It records where the pattern string should continue to match when the original string does not match the pattern string.
2.1 definition of prefix and suffix
- Prefix: for a string, substrings that contain the first character but not the last character are called prefixes
- Suffix: for a string, substrings that contain the trailing character but not the first character are called suffixes
For example, find the prefix of the string "abcdef".
Prefixes are: "a", "ab", "abc", "abcd", "abcde"
Suffixes are: "f", "ef", "def", "cdef", "bcdef"
After knowing the definition of pre suffix, let's take a look at the above matching process.
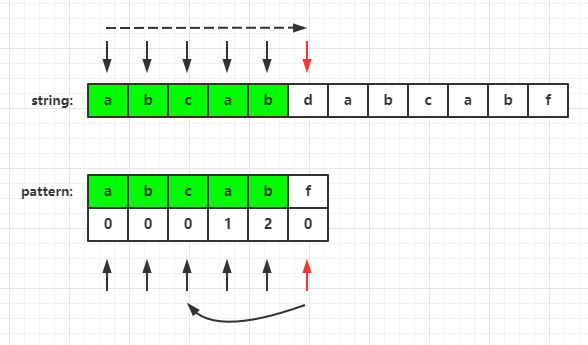
As shown in the figure, there is a conflict between d and f. let's take a look at the prefix and suffix of the pattern string and the longest matching Prefix suffix.
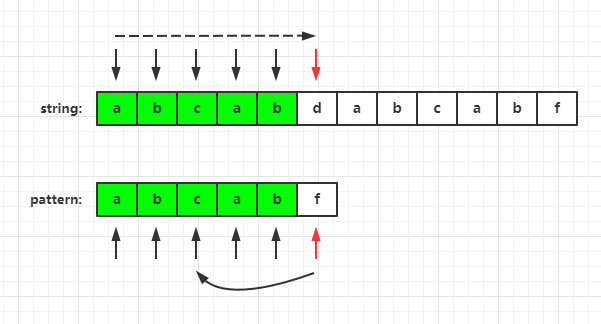
Because 'f' has been matched, let's look at the prefix of "abcab"
Prefixes are: "a", "ab", "abc", "abca"
The suffixes are: "b", "ab", "cab", "bcab"
Longest matching prefix: "ab"
Why look at the longest matching prefix?
First of all, because the prefix must start from 0. If the string in front of the current character has the longest matching prefix, it means that there is a string in front of f that is the same as the prefix, then we can continue to match from the next character of the prefix. As shown in the figure:
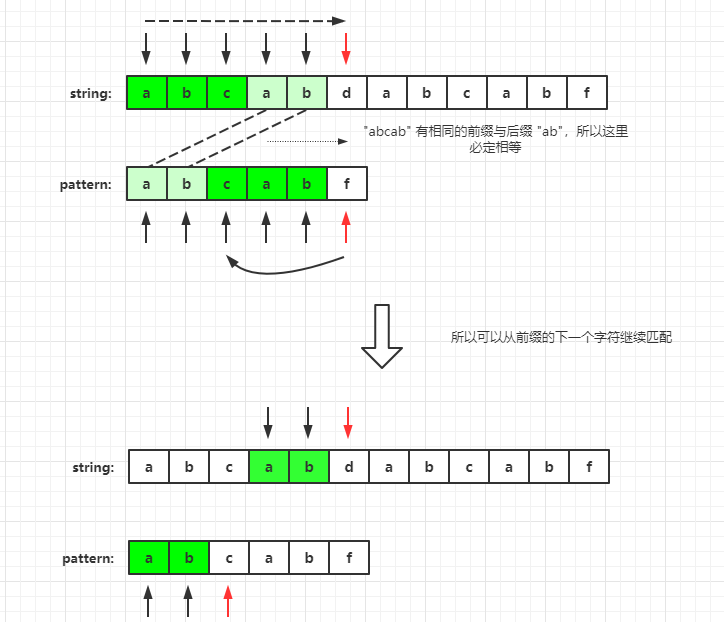
For the above figure, we set the current matching index of string as sidx and the current matching index of pattern as pidx. When string [sidx]= When pattern [pidx], we can find the longest pre matching suffix of pattern[0, pidx - 1] string, and return pidx to the next position of prefix to continue matching. Make the following judgment.
Longest matching prefix + pattern[pidx] == Longest matching suffix + string[sidx]
If pattern[pidx] == string[sidx], it means that the above judgment is true and continue to match, otherwise it is false. Repeat the operation of returning pidx to the next position of the prefix to continue matching.
2.2 what is the prefix table (next)
The prefix table is generated according to the pattern string pattern, which records the string of current length "the longest matching length between prefix and suffix", so you can quickly locate where the pattern string should continue to match through this prefix table.
Through the description of the matching length between the preceding suffix and the longest preceding suffix above, it is not difficult to write the prefix table of the pattern in the above matching process:
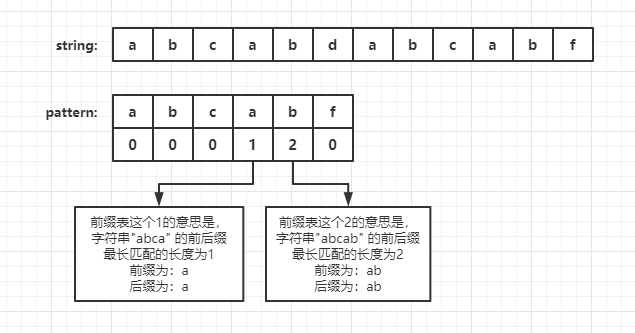
Then, when the original conflicts with the pattern string, you can quickly find where to continue matching through the prefix table.
for instance
When there is a conflict between'd 'and' f ', we can quickly find out whether the string in front of F has the same pre suffix through the prefix table. If it continues to match from the next character of the prefix, that is, f finds whether there is the same longest pre suffix in "abcab", and the longest matched pre suffix length of this character string is saved in the prefix table of the subscript of the last character, That is, next[indexOf('f') - 1] is the longest matching prefix length of "abcab". It can be seen that the longest matching prefix length is 2, so the position of continuing matching is the third of the pattern string, that is, pattern[2]. (in fact, there is a reason why the subscript to continue matching here is the longest pre suffix length, because the subscript of pattern array starts from 0)
Then, after understanding the function and generation principle of prefix table (next), let's see how to generate prefix table.
2.3 how to generate prefix table
From the previous description, we can know that the prefix and suffix are the same string, as shown in the figure.
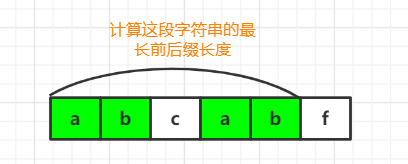
Then we can use a prefix pointer to mark the last character of the prefix and a suffix pointer to mark the last character of the suffix. The value of the prefix pointer is the length of the prefix, that is, the length of the prefix such as the longest phase.
We remember that the prefix pointer is prefixIdx and the suffix pointer is suffixIdx. Then simulate the process of building prefix table.
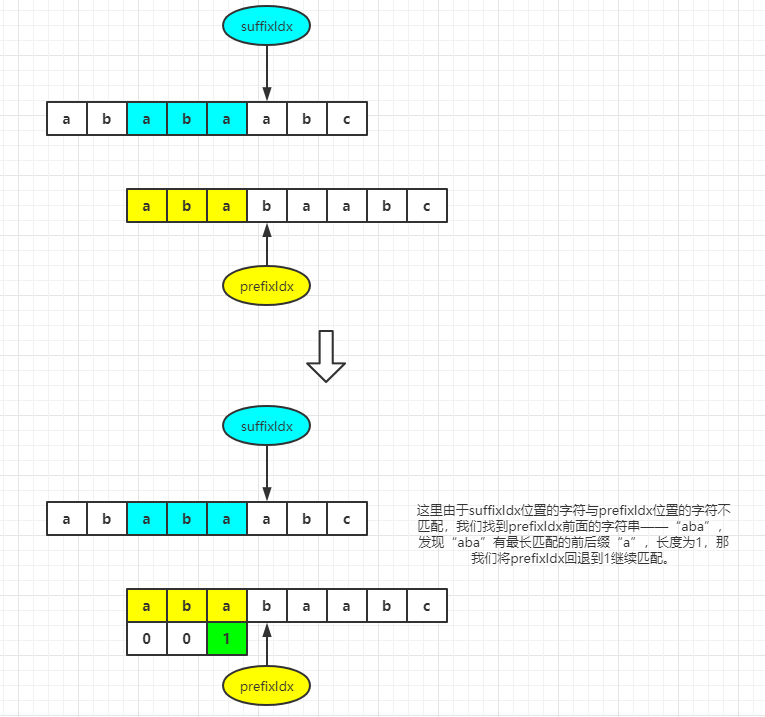
Let's simulate a long prefix table generation process. The pattern string is "ababaabc"
(1) First of all, because there is no prefix and suffix when there is only one character, the minimum length of the prefix and suffix that can be generated is 2. Then we can omit the case of prefixIdx == suffixIdx and stagger the two indexes, then we can set the initial value for prefixIdx and suffixIdx.
prefixIdx = 0; suffixIdx = 1;
(2) in the second step, judge whether the character referred to by prefixIdx is the same as that referred to by suffixIdx
- pattern[prefixIdx] == pattern[suffixIdx]
- pattern[prefixIdx] != pattern[suffixIdx]
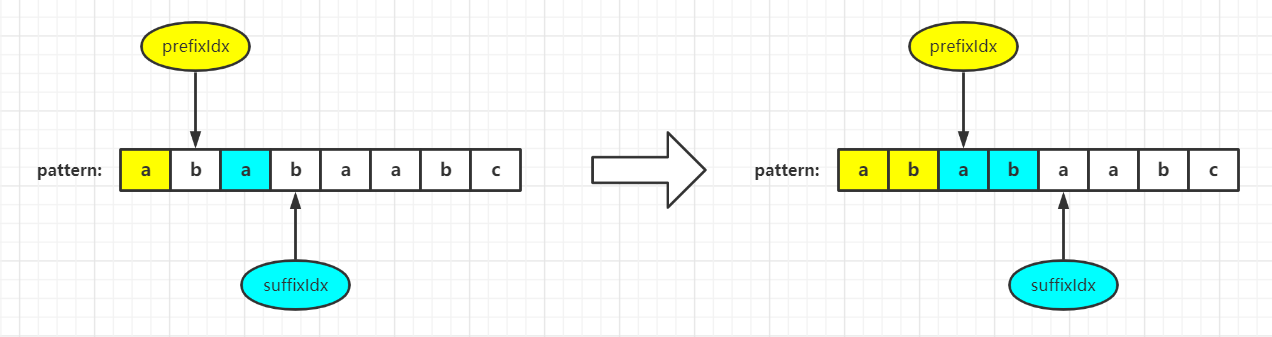
For pattern[prefixIdx] == pattern[suffixIdx]
It shows that this character can form a new longest prefix with the previous prefix string. Then we can directly add one to both prefixIdx and suffixIdx to compare the next character. As shown in the figure:
For pattern [prefixidx]= pattern[suffixIdx]
It indicates that this character cannot form a new longest phase and other pre suffix with the previous prefix string. At this time, we need to find a new longest phase and other pre suffix again. The construction logic of this situation is a little difficult to understand and explain. For ease of explanation, we assume that prefixIdx and suffixIdx traverse the same two strings. As shown in the figure:
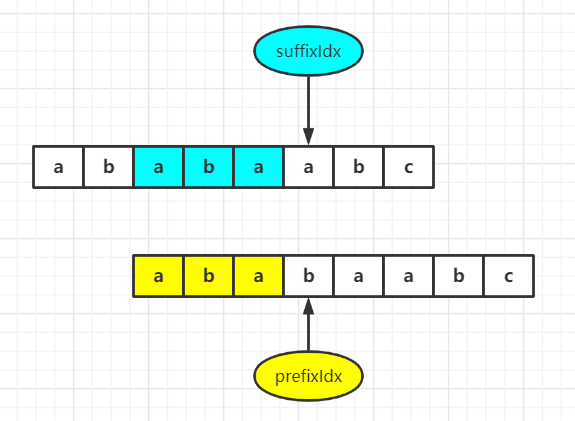
When traversing here, we find pattern [prefixidx]= Pattern [suffixidx], at this time, we have to find the longest matching prefix and suffix again. How do we know where to start again?
First of all, the prefix must start from 0, and our suffix must also start from the pattern[0] character. Our main task is to find the position of the pattern[0] character and re match it to suffixIdx from that position. Does this look like a matching process in a string?
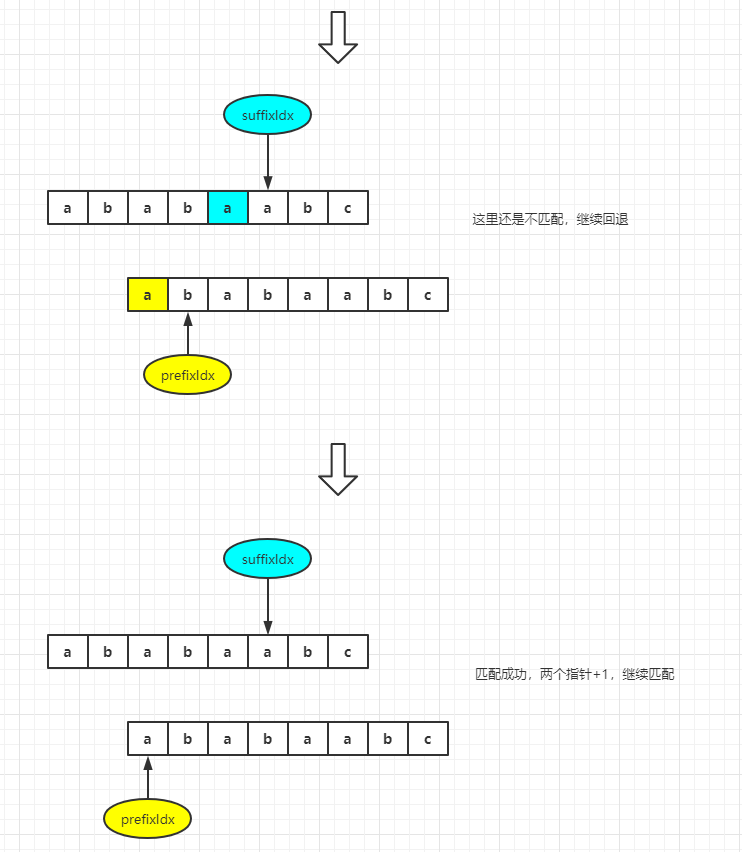
In fact, this process is very similar to matching prefix strings in strings
- If the match is successful, the current prefix string is the longest matching prefix length. Continue to match the prefix of the next length
- If the matching fails, you need to find the next matching position of suffixIdx and continue the matching. If a suffix containing pattern[suffixIdx] is matched, the length of this suffix is the longest matching pre suffix length. Otherwise, if there is no matching pre suffix, continue to match the prefix of the next length.
It is not difficult to understand the success of matching. Why can we do this for the failure of matching?
We have talked about the related pre suffix and the knowledge of the longest matching pre suffix. So let's imagine that when the characters of prefixIdx and suffixIdx are different, can we find the longest pre matching suffix of the string in front of the suffixIdx character and return the prefixIdx to the next matching position to continue matching.
(1) If pattern[prefixIdx] == pattern[suffixIdx], it means that the length of the prefix is the length of the longest matching pre suffix at this time, because prefixIdx returns to the next character of the longest matching pre suffix in the previous string. That is, (longest matching prefix + pattern[prefixIdx] = = longest matching suffix + pattern[suffixIdx]) = true
(2) If pattern [prefixIdx]= Pattern [suffixidx], continue to return prefixIdx to the next matching position and continue to repeat the operation.
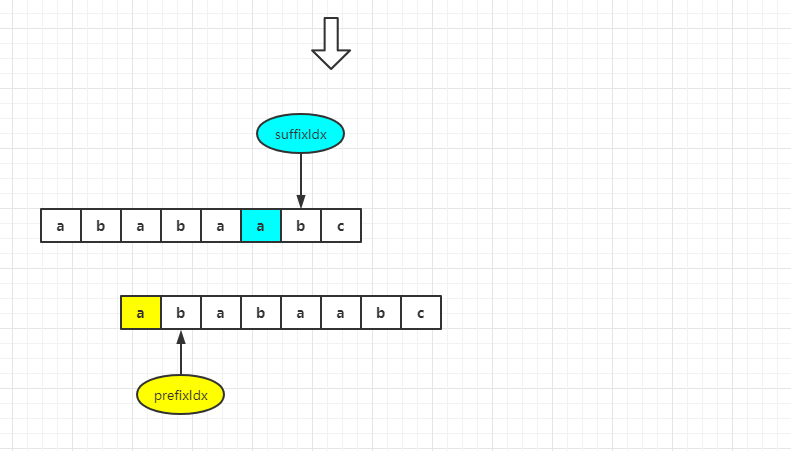
At this point, we can write the code to build the prefix table
public int[] buildNext(String pattern) {
int plen = pattern.length();
int[] next = new int[plen];
for (int prefixIdx = 0, suffixIdx = 1; suffixIdx < plen; suffixIdx++) {
while (prefixIdx > 0 && pattern.charAt(prefixIdx) != pattern.charAt(suffixIdx)) {
prefixIdx = next[prefixIdx - 1];
}
if (pattern.charAt(prefixIdx) == pattern.charAt(suffixIdx)) {
prefixIdx++;
}
next[suffixIdx] = prefixIdx;
}
return next;
}After knowing the code of prefix table, the code of KMP is simple.
3. Complete KMP code
// KMP algorithm
// String: original string pattern: pattern string
public int strStr(String string, String pattern) {
if (pattern == null || pattern.length() == 0) {
return 0;
}
int slen = string.length();
int plen = pattern.length();
int[] next = buildNext(pattern);
for (int sidx = 0, pidx = 0; sidx < slen; sidx++) {
while (pidx > 0 && string.charAt(sidx) != pattern.charAt(pidx)) {
pidx = next[pidx - 1];
}
if (string.charAt(sidx) == pattern.charAt(pidx)) {
pidx++;
}
if (pidx == plen) {
return sidx - plen + 1;
}
}
return -1;
}
public int[] buildNext(String pattern) {
int plen = pattern.length();
int[] next = new int[plen];
for (int prefixIdx = 0, suffixIdx = 1; suffixIdx < plen; suffixIdx++) {
while (prefixIdx > 0 && pattern.charAt(prefixIdx) != pattern.charAt(suffixIdx)) {
prefixIdx = next[prefixIdx - 1];
}
if (pattern.charAt(prefixIdx) == pattern.charAt(suffixIdx)) {
prefixIdx++;
}
next[suffixIdx] = prefixIdx;
}
return next;
}