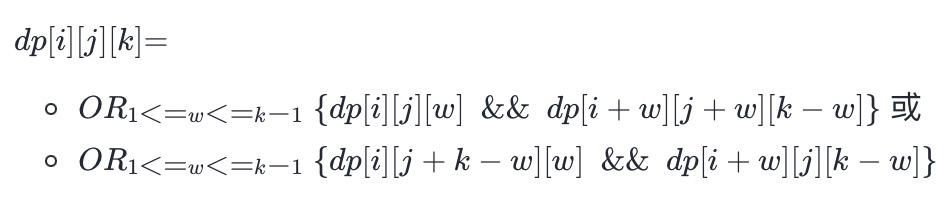1. Title requirements

• Using the algorithm described below, you can scramble the string s to get the string t:
• • If the length of the string is 1, the algorithm stops.
• • If the length of the string is > 1, perform the following steps:
• • • Split a string into two non-empty substrings at a random subscript. That is, if the string s is known, it can be divided into two substrings, X and y, satisfying s = x + y;
• • • Randomly decide whether to "swap two substrings" or "keep the order of the two substrings unchanged". That is, after performing this step, s may be s = x + y or s = y + x;
• • • Continue to recursively execute the algorithm from step 1 on the substrings x and y.
• Give you two equally long strings S1 and s2 to determine if s2 is a scrambled string of s1. If so, return true; Otherwise, return false.
• Example 1:

Input: s1 = "great", s2 = "rgeat"
Output: true
 Explanation: s1 One possible scenario is:
"great" --> "gr/eat" // Split two substrings at a random subscript
"gr/eat" --> "gr/eat" // Random decision: "Keep these two substrings in the same order"
"gr/eat" --> "g/r / e/at" // The algorithm is executed recursively on the substring. Two substrings are split one round at random Subscripts
"g/r / e/at" --> "r/g / e/at" // Random decision: the first group "swap two substrings" and the second group "keep the order of the two substrings unchanged."
"r/g / e/at" --> "r/g / e/ a/t" // Continue executing the algorithm recursively, splitting "a t" into "a/t"
"r/g / e/ a/t" --> "r/g / e/ a/t" // Random decision: "Keep these two substrings in the same order"
Algorithm termination, result string and s2 Same, both "rgeat"
This is one that can disrupt s1 obtain s2 The situation can be thought of as s2 yes s1 Disturbing string, returned true

• Example 2:

Input: s1 = "abcde", s2 = "caebd"
Output: false

• Example 3:

Input: s1 = "a", s2 = "a"
Output: true

• Tips:
• • s1.length == s2.length；
• • 1 <= s1.length <= 30；
• • s1 and s2 are composed of lower case English letters.

2. Solving algorithm

(1) Dynamic planning

• Given two strings T and S, suppose T is transformed from S:
• • If the lengths of T and S are not the same, they must not change.
• • If the length is the same, the top string S can be divided into S1 and S 2, and the string T can also be divided into T1 and T2.
• • • Case 1: No exchange, S1 ==> T1, S2 ==> T2;
• • • Scenario 2: Exchanged, S1 ==> T2, S2 ==> T1;
• The sub-question is whether T1 changes from S1, T2 from S2, or T1 from S2, and T2 from S1.

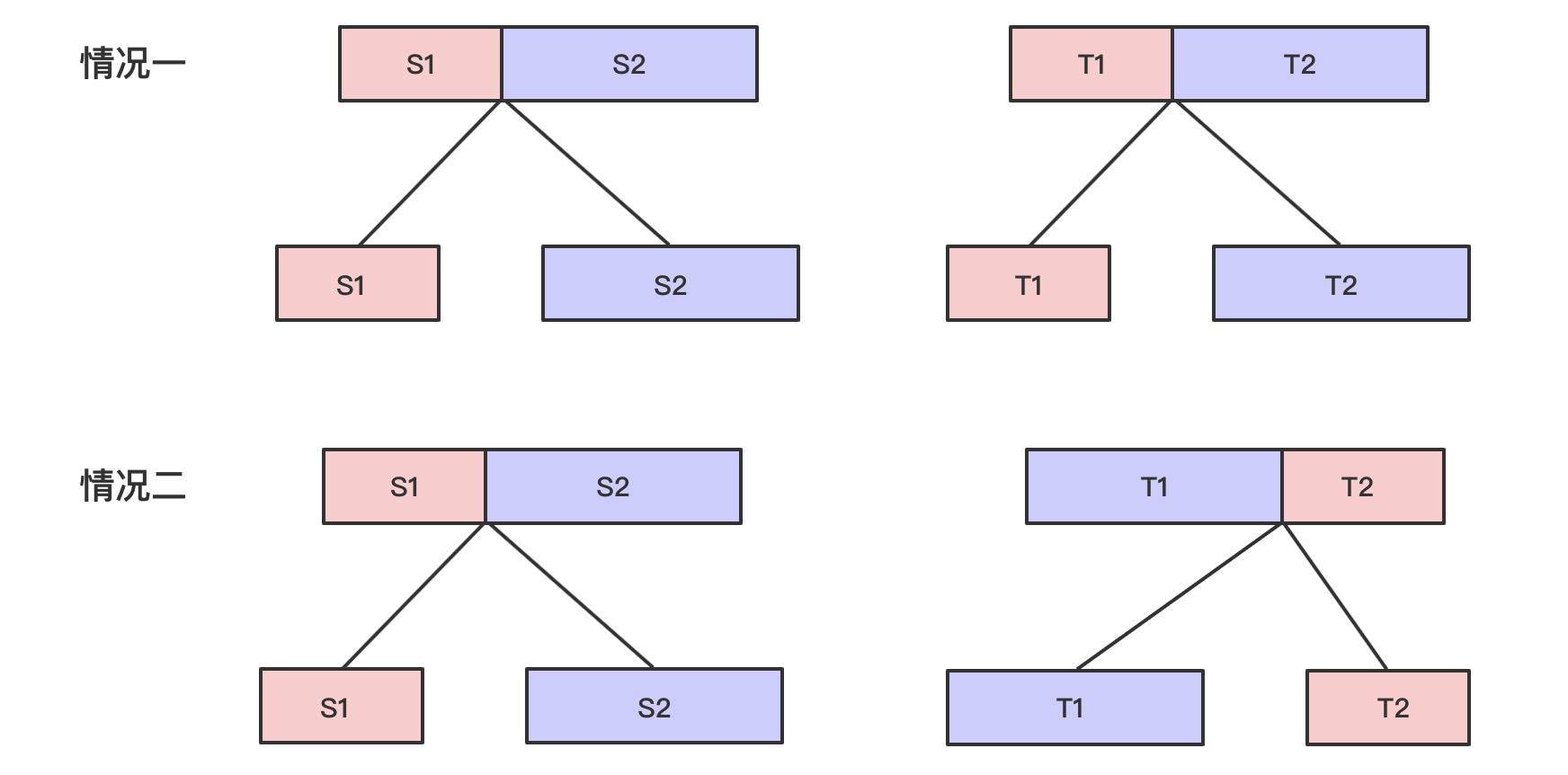
• dp[i][j][k][h] indicates whether T[k...h] is changed from S[i...j]. Since the transformations must have the same length, there is a relationship j_i=h_k on this side, which reduces the four-dimensional array to three dimensions. dp[i][j][len] indicates whether a string starting with len from I in string S can be converted to a string starting with len from J in string T.
• Transfer equation:

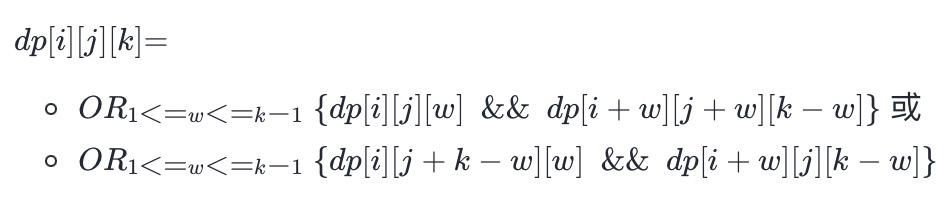
• Enumerating the length of S1 w (from 1 to k_1 because of division), f[i][j][w] indicates that S1 can become T1, f[i+w][j+w][k_w] indicates that S2 can become T2, or S1 can become T2, and S2 can become T1.
• Initial condition: For a substring of length 1, only equality can pass, equality is true, and inequality is false.
• Java example:

class Solution {
    public boolean isScramble(String s1, String s2) {
        char[] chs1 = s1.toCharArray();
        char[] chs2 = s2.toCharArray();
        int n = s1.length();
        int m = s2.length();
        if (n != m) {
            return false;
        }
        boolean[][][] dp = new boolean[n][n][n + 1];
        // Initialization of a single character
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                dp[i][j][1] = chs1[i] == chs2[j];
            }
        }

        // Enumeration interval length 2~n
        for (int len = 2; len <= n; len++) {
            // Enumerate starting position in S
            for (int i = 0; i <= n - len; i++) {
                // Enumerate starting position in T
                for (int j = 0; j <= n - len; j++) {
                    // Enumerate partition positions
                    for (int k = 1; k <= len - 1; k++) {
                        // First case: S1 -> T1, S2 -> T2
                        if (dp[i][j][k] && dp[i + k][j + k][len - k]) {
                            dp[i][j][len] = true;
                            break;
                        }
                        // Second case: S1 -> T2, S2 -> T1
                        // S1 start i, T2 start j +the length len-k before, S2 start I +the length k before
                        if (dp[i][j + len - k][k] && dp[i + k][j][len - k]) {
                            dp[i][j][len] = true;
                            break;
                        }
                    }
                }
            }
        }
        return dp[0][0][n];
    }
}

class Solution {
    public boolean isScramble(String s1, String s2) {
        // Length is not equal and must not be transformed
        if (s1.length() != s2.length()) {
            return false;
        }
        // Equal length, first decided
        if (s1.equals(s2)) {
            return true;
        }
        // See if the number of characters is consistent, but not directly return false
        int n = s1.length();
        HashMap<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            char c1 = s1.charAt(i);
            char c2 = s2.charAt(i);
            map.put(c1, map.getOrDefault(c1, 0) + 1);
            map.put(c2, map.getOrDefault(c2, 0) - 1);
        }
        for (Character key : map.keySet()) {
            if (map.get(key) != 0) {
                return false;
            }
        }

        // In the same way, start judging and one will return true
        for (int i = 1; i < n; i++) {
            boolean flag =
                    // S1 -> T1，S2 -> T2
                    (isScramble(s1.substring(0, i), s2.substring(0, i)) && isScramble(s1.substring(i), s2.substring(i))) ||
                    // S1 -> T2，S2 -> T1
                    (isScramble(s1.substring(0, i), s2.substring(n - i)) && isScramble(s1.substring(i), s2.substring(0, s2.length() - i)));
            if (flag) {
                return true;
            }
        }
        return false;
    }
}

(2) Simple Solution (TLE)

• One simple way to judge this is based on the "Disturbing String" generation rule, since the title says that the entire process of generating the "Disturbing String" is through "recursion". The purpose of implementing the isScramble function is to determine if s1 can produce s2.
• We can also use "recursion" to make this judgment: assuming that the length of s1 i s n and the first split point i s i, s1 will be divided into [0, i] and [i, n]. At the same time, when "scrambling string" i s generated, swapping i s optional or not, so there are two possibilities for our s2:

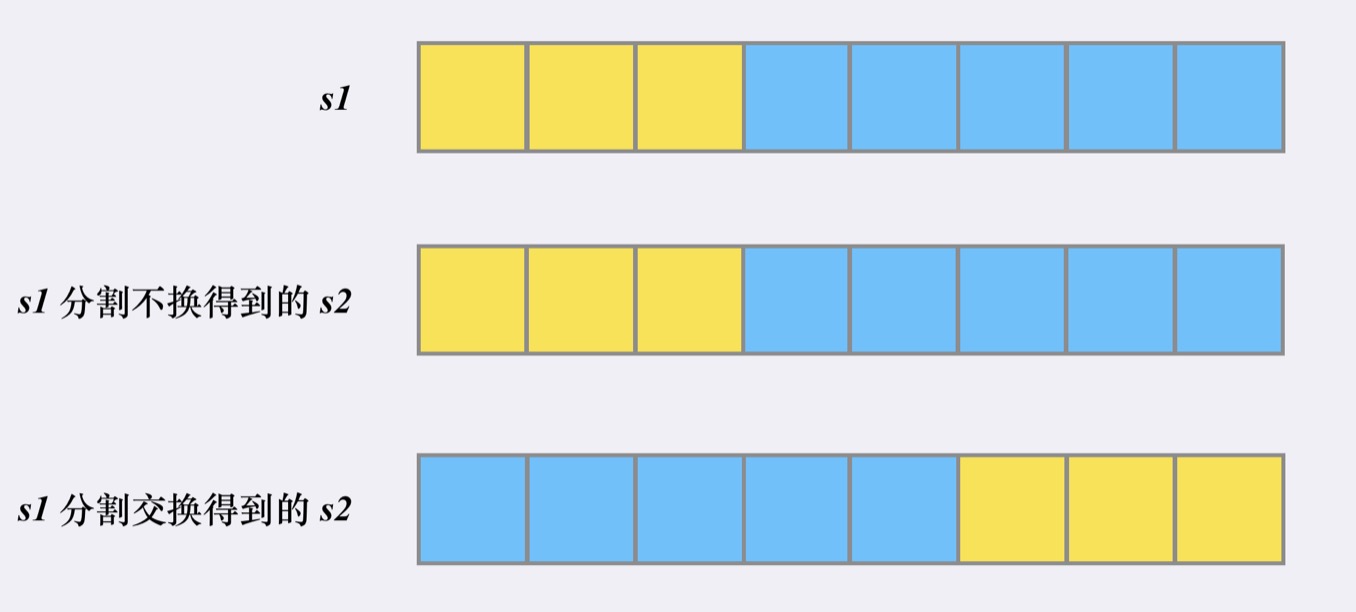
• Because for a given split point, s1 is fixed i n two parts, [0, i] & [i, n]. s2 may have two ways of splitting, [0, i] & [i, n] and [0,n_i] & [n_i, n].
• Simply recursively call isScramble to check if the [0, i] & [i,n) portion of s1 can match the [0, i] & [i, n] portion of S2 or the [0,n_i] & [n_i, n] portion of s2.
• At the same time, "s1 and s2 are equal" and "s1 and s2 have different word frequencies" are used as "recursive" exports.
• Java example:

class Solution {
    public boolean isScramble(String s1, String s2) {
        if (s1.equals(s2)) return true;
        if (!check(s1, s2)) return false;
        int n = s1.length();
        for (int i = 1; i < n; i++) {
            // [0, i] and [i, n] of s1
            String a = s1.substring(0, i), b = s1.substring(i);
            // [0, i] and [i, n] of s2
            String c = s2.substring(0, i), d = s2.substring(i);
            if (isScramble(a, c) && isScramble(b, d)) return true;
            // [0, n-i] and [n-i, n] of s2
            String e = s2.substring(0, n - i), f = s2.substring(n - i);
            if (isScramble(a, f) && isScramble(b, e)) return true;
        }
        return false;
    }
    // Check if s1 and s2 word frequencies are the same
    boolean check(String s1, String s2) {
        if (s1.length() != s2.length()) return false;
        int n = s1.length();
        int[] cnt1 = new int[26], cnt2 = new int[26];
        char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
        for (int i = 0; i < n; i++) {
            cnt1[cs1[i] - 'a']++;
            cnt2[cs2[i] - 'a']++;
        }
        for (int i = 0; i < 26; i++) {
            if (cnt1[i] != cnt2[i]) return false;
        }
        return true;
    }
}