Accessibility analysis of Gauss two-step mobile search method based on road network and GeoPandas

import warnings
warnings.filterwarnings("ignore")
import geopandas as gpd
import pandas as pd
import os
import collections
import heapq
import re
import math

# File path
path=r"C:\Users\Falling flower rain\Desktop\data"
LIST=["\\"+i for i in os.listdir(path)]

KM_Poi=gpd.read_file(path+LIST[5]) # Kunming points of interest
YJBNS_Ent=gpd.read_file(path+LIST[2]) # Emergency shelter entrance data
YJBNS_Polgon=gpd.read_file(path+LIST[3]) # Data of emergency shelter
ZCQ_Roa=gpd.read_file(path+LIST[1]) # Main urban roads
OD=gpd.read_file(path+LIST[0])# OD matrix

Data exploration

KM_Poi.head(2)

	FID	OBJECTID	osm_id	name	type	population	QUYU_NAME	geometry
0	0	3	474552927	Guandu Street	town	183624	public ferry	POINT (576290.931 2761828.261)
1	1	12	1483174846	Haikou Street	town	69019	Xishan	POINT (561304.355 2742770.016)

YJBNS_Ent.head(2)

	FID	OBJECTID	NAME	QUYU_NAME	geometry
0	0	6	Chenggong campus of Yunnan University - West Gate	Chenggong	POINT (585001.518 2747248.457)
1	1	7	Chenggong campus of Yunnan University - North Gate	Chenggong	POINT (585528.681 2748211.540)

YJBNS_Polgon.head(2)

	FID	NAME	Shape_Leng	Shape_Area	geometry
0	0	Radio and television garden campus of the first primary school in Chenggong New Area, Kunming	610.369700	19710.134256	POLYGON ((11444231.072 2852271.929, 11444275.0...
1	1	Kunming Experimental School Affiliated to Sichuan Normal University (days)	966.366133	52802.239035	POLYGON ((11445552.439 2854525.840, 11445615.3...

ZCQ_Roa.head(2)

	FID	FID_roads	osm_id	name	ref	type	oneway	bridge	maxspeed	FID_ Kunming	...	name_1	center	centroid	childrenNu	level	parent	subFeature	acroutes	length	geometry
0	0	0	23412703.0	Kunming-Shilin Expressway		motorway	1	1	0	2	...	Guandu District	0	0	0	district	0	2	0	1152.168205	MULTILINESTRING ((102.73576 25.01994, 102.7363...
1	1	1	24044953.0	Baita Road		secondary	1	0	0	1	...	Panlong District	0	0	0	district	0	1	0	1994.046225	MULTILINESTRING ((102.72596 25.05293, 102.7260...

2 rows × 21 columns

Data preprocessing

# View coordinate system
KM_Poi.crs # The point of interest is CGCS2000 / 3-degree Gauss Kruger cm 102e
# Its coordinate system code is 4543

<Projected CRS: EPSG:4543>
Name: CGCS2000 / 3-degree Gauss-Kruger CM 102E
Axis Info [cartesian]:
- X[north]: Northing (metre)
- Y[east]: Easting (metre)
Area of Use:
- name: China - between 100°30'E and 103°30'E.
- bounds: (100.5, 21.13, 103.5, 42.69)
Coordinate Operation:
- name: 3-degree Gauss-Kruger CM 102E
- method: Transverse Mercator
Datum: China 2000
- Ellipsoid: CGCS2000
- Prime Meridian: Greenwich

ZCQ_Roa.crs
# The coordinate system of Road needs to be converted into projection coordinates

<Geographic 2D CRS: GEOGCS["CGCS_2000",DATUM["D_2000",SPHEROID["S_2000 ...>
Name: CGCS_2000
Axis Info [ellipsoidal]:
- lon[east]: Longitude (Degree)
- lat[north]: Latitude (Degree)
Area of Use:
- undefined
Datum: D_2000
- Ellipsoid: S_2000
- Prime Meridian: Greenwich

YJBNS_Polgon.crs  # The emergency shelter is WGS84
# Coordinate conversion required

<Projected CRS: EPSG:3857>
Name: WGS 84 / Pseudo-Mercator
Axis Info [cartesian]:
- X[east]: Easting (metre)
- Y[north]: Northing (metre)
Area of Use:
- name: World between 85.06°S and 85.06°N.
- bounds: (-180.0, -85.06, 180.0, 85.06)
Coordinate Operation:
- name: Popular Visualisation Pseudo-Mercator
- method: Popular Visualisation Pseudo Mercator
Datum: World Geodetic System 1984 ensemble
- Ellipsoid: WGS 84
- Prime Meridian: Greenwich

OD.crs

<Projected CRS: EPSG:4543>
Name: CGCS2000 / 3-degree Gauss-Kruger CM 102E
Axis Info [cartesian]:
- X[north]: Northing (metre)
- Y[east]: Easting (metre)
Area of Use:
- name: China - between 100°30'E and 103°30'E.
- bounds: (100.5, 21.13, 103.5, 42.69)
Coordinate Operation:
- name: 3-degree Gauss-Kruger CM 102E
- method: Transverse Mercator
Datum: China 2000
- Ellipsoid: CGCS2000
- Prime Meridian: Greenwich

YJBNS_Ent.crs

<Projected CRS: EPSG:4543>
Name: CGCS2000 / 3-degree Gauss-Kruger CM 102E
Axis Info [cartesian]:
- X[north]: Northing (metre)
- Y[east]: Easting (metre)
Area of Use:
- name: China - between 100°30'E and 103°30'E.
- bounds: (100.5, 21.13, 103.5, 42.69)
Coordinate Operation:
- name: 3-degree Gauss-Kruger CM 102E
- method: Transverse Mercator
Datum: China 2000
- Ellipsoid: CGCS2000
- Prime Meridian: Greenwich

Coordinate system conversion

YJBNS_Polgon=YJBNS_Polgon.to_crs(epsg=4543)
ZCQ_Roa=ZCQ_Roa.to_crs(epsg=4543)
YJBNS_Ent=YJBNS_Ent.to_crs(epsg=4543)

At this time, the work of unifying the coordinate system has been completed

Step 1 Calculation

This step needs to find out all POI s within the search radius of the emergency shelter and calculate the supply-demand ratio

Build buffer

The buffer is used to search for supply points

YJBNS_Polgon_C=YJBNS_Polgon.copy()

# Build buffer example
YJBNS_Polgon_C["geometry"][0].buffer(50)

# We don't need a middle
YJBNS_Polgon_C["geometry"][0].buffer(50).difference(YJBNS_Polgon_C["geometry"][0])

# Check the distribution of emergency shelters
YJBNS_Polgon_C['geometry'].plot()

<matplotlib.axes._subplots.AxesSubplot at 0x1c7f17706d8>

# Set buffer radius
BUFFER=3000

YJBNS_Polgon_C['geometry']=YJBNS_Polgon_C["geometry"].buffer(BUFFER)

YJBNS_Polgon_C['geometry'].plot()

<matplotlib.axes._subplots.AxesSubplot at 0x1c7f178ab00>

Manhattan distance

Compared with European distance measurement, Manhattan distance can better reflect the actual connectivity between urban POI s

OD.head(2)

	FID	ObjectID	Name	OriginID	Destinatio	Destinat_1	Total_ long	geometry
0	0	12851	Guandu Street - century Jinyuan School Affiliated to Yunnan Normal University - East Gate	103	422	1	1296.528731	LINESTRING (576290.931 2761828.261, 575577.741...
1	1	12852	Guandu Street - Xingyao campus of Yunda affiliated middle school - North Gate	103	420	2	1490.718704	LINESTRING (576290.931 2761828.261, 577144.590...

For OD cost matrix, we hope to have a settlement for each emergency shelter

In the constructed OD matrix, the Name attribute is divided by street emergency shelter entrance

# Get name list first
Ent_name_list=YJBNS_Ent["NAME"].unique()
Str_name_list=KM_Poi["name"].unique()

S2E=collections.defaultdict(list)# Street entry dictionary
E2S=collections.defaultdict(list) # Street dictionary corresponding to entrance

for i in range(OD.shape[0]):
    # Get and split names
    Name=list(map(lambda x:x.strip(),OD.iloc[i,2].split("-",1)))
    # Record the corresponding value
    dis=OD.iloc[i,6]
    # street
    # The data will be repeatedly read and written three times!!
    # Do not know why?
    heapq.heappush(S2E[Name[0]],(dis,Name[1]))
    heapq.heappush(E2S[Name[1]],(dis,Name[0]))

# At this time, it is found that all records have been recorded
for i in Ent_name_list:
    if i not in E2S.keys():
        print(E2S[i])
        
# Ma Street is a fairy
# He was abandoned because he couldn't find his destination
for j in Str_name_list:
    if j not in S2E.keys():
        print(j)

Ma Jie Street

# The small root heap will weed out the elements
# If you want to keep the element, you can leave a copy
S2E_c=S2E.copy()
E2S_c=E2S.copy()

At this point, we have dealt with the Manhattan distance, and now we can start from the entrance of the shelter to find the settlement with a given threshold

It can also start from the residential area and find the service area with a given threshold

Next, we will get the area information of the shelter

Area of emergency shelter

In this step, we need to obtain the area information of the emergency shelter and correspond it with the entry point

Let's look at the shelter data first

YJBNS_Polgon_C1=YJBNS_Polgon.copy()
YJBNS_Polgon_C1.plot()

<matplotlib.axes._subplots.AxesSubplot at 0x1c7f17a6128>

YJBNS_Polgon_C1.head()

	FID	NAME	Shape_Leng	Shape_Area	geometry
0	0	Radio and television garden campus of the first primary school in Chenggong New Area, Kunming	610.369700	19710.134256	POLYGON ((581419.907 2745109.067, 581460.202 2...
1	1	Kunming Experimental School Affiliated to Sichuan Normal University (days)	966.366133	52802.239035	POLYGON ((582607.927 2747151.992, 582666.062 2...
2	2	Emergency shelter of Yunnan University of traditional Chinese Medicine	3778.904004	607319.343216	POLYGON ((582979.894 2749463.449, 582932.370 2...
3	3	Laoyuhe Wetland Park	3832.693417	513661.330361	POLYGON ((577548.739 2746297.639, 577654.965 2...
4	4	High school attached to Yunshi University	1255.955110	107052.706438	POLYGON ((585882.850 2749957.852, 585741.543 2...

After data exploration, it is found that the NAME attribute column in the data can correspond to the entry NAME, and the Shape_Area is the area obtained by geometric calculation

However, the names between the two tables do not exactly match. We just need to match keywords

# Array to be mapped
E_N=E2S.keys()
P_N=YJBNS_Polgon_C1["NAME"]

Name_Area=[]
for i in P_N:
    for j in E_N:
        if re.search(i,j):
            Name_Area.append([j,(YJBNS_Polgon_C1[YJBNS_Polgon_C1["NAME"]==i]["Shape_Area"]).tolist()[0]])

# Create a query table
Area=dict(Name_Area)

Now we need to design a function to extract the data within a given threshold

def getData(dataset,threshold):
    tem_dataset=dataset.copy()
    if len(tem_dataset)==0:
        # Empty table
        return []
    T=heapq.heappop(tem_dataset)
    ans=[]
    while T[0]<=threshold:
        ans.append(T)
        T=heapq.heappop(tem_dataset)
    return ans

Population data

The Population data is stored in the Population field of Kunming POI

KM_Poi.head()

	FID	OBJECTID	osm_id	name	type	population	QUYU_NAME	geometry
0	0	3	474552927	Guandu Street	town	183624	public ferry	POINT (576290.931 2761828.261)
1	1	12	1483174846	Haikou Street	town	69019	Xishan	POINT (561304.355 2742770.016)
2	2	14	-1995559001	Majinpu Street	town	54798	Chenggong	POINT (581339.943 2742863.779)
3	3	15	-1659466282	Ala Street	town	87545	public ferry	POINT (579586.509 2766116.964)
4	5	22	-782694876	Shuanglong Street	town	11841	Panlong	POINT (585541.983 2778974.166)

To view its population data, you only need the following statement

KM_Poi[KM_Poi["name"]=="Guandu Street"]["population"].tolist()[0]

# Encapsulate into function
def getPop(name):
    try:
        return KM_Poi[KM_Poi["name"]==name]["population"].tolist()[0]
    except:
        return -1
    
# But the time complexity is too high
# So I decided to type my watch
Name_Pop={}
for i in range(KM_Poi.shape[0]):
    T=KM_Poi.iloc[i]
    Name_Pop[T['name']]=T['population']

Supply demand ratio calculation

According to the formula:
R j = S j ∑ k ∈ { d k j ≤ d 0 } G ( d k j , d 0 ) D k R_j =\frac{S_j}{\sum_{k\in \{{d_{kj}\le d_0}\}}G(d_{kj},d_0)D_k} Rj=∑k∈{dkj≤d0}G(dkj,d0)DkSj
Calculate

# First determine the search radius
# This demo uses the search radius of the given threshold
Threshold=3000
# test
getData(S2E_c["Guandu Street"],Threshold)

[(1296.52873128, 'Century Jinyuan School Affiliated to Yunnan Normal University-East Gate'),
 (1490.71870426, 'Xingyao campus of Yunda affiliated middle school-North Gate'),
 (1600.79115752, 'Yunyao Campus-South Gate'),
 (1708.15483322, 'Xingyao campus of Yunda affiliated middle school-1 Gate No'),
 (1782.80973124, 'Century Jinyuan School Affiliated to Yunnan Normal University-Southwest gate'),
 (1850.44174205, 'Century Jinyuan School Affiliated to Yunnan Normal University-west gate'),
 (1955.38161, 'Century Jinyuan School Affiliated to Yunnan Normal University-Northwest Gate'),
 (2780.42288513, 'New Asia Sports City Sports Center-2 Gate No'),
 (2960.49871649, 'New Asia Sports City Sports Center-1 Gate No')]

# test
getData(E2S_c["Radio and television garden campus of the first primary school in Chenggong New Area, Kunming"],12000)

[(3219.24822336, 'Majinpu Street'),
 (3354.50862843, 'Dayu Street'),
 (5100.55004948, 'Yuhua Street'),
 (8610.87021572, 'Oolong Street'),
 (9965.30536041, 'Longcheng Street'),
 (10175.1377117, 'Luolong Street')]

What we need to deal with now is to accumulate these data according to the formula and determine the Gaussian method first:

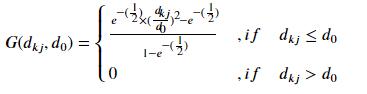
def Gauss(dis,dis_D):
    f1=((math.e)**(-0.5))*((dis/dis_D)**2)-math.e*(-0.5)
    f2=1-math.e**(-0.5)
    return f1/f2

# Calculate for each supply point
# Keep copies
YJBNS_Ent_c=YJBNS_Ent.copy()
R_list=[] # Used to store data

for i in range(len(Ent_name_list)):
    # Find each demand point within the search radius
    name=YJBNS_Ent_c.iloc[i,2]
    points=getData(E2S[name],Threshold)
    # Of course, some don't have it at all
    # In this part, we will improve the algorithm later
    # We need to get the population of these points
    ans=0
    for poi in points:
        Name=poi[1]
        dis=poi[0]
        population=Name_Pop[Name]
        ans+=population*Gauss(dis,Threshold)
    # Those that cannot be found need to be handled
    # In fact, our data are not completely one-to-one correspondence
    try:
        R_list.append(Area[name]/ans)
    # At present, for division by zero (there are no points in the search radius of this area)
    # And area mismatch (missing shelter area)
    # Unified zeroing
    except:
        R_list.append(0)

YJBNS_Ent_c['R_val']=R_list
YJBNS_Ent_c.head()

	FID	OBJECTID	NAME	QUYU_NAME	geometry
0	0	6	Chenggong campus of Yunnan University - West Gate	Chenggong	POINT (585001.518 2747248.457)
1	1	7	Chenggong campus of Yunnan University - North Gate	Chenggong	POINT (585528.681 2748211.540)
2	2	8	Chenggong campus of Yunnan University - East Gate	Chenggong	POINT (586966.101 2747785.881)
3	3	9	Chenggong campus of Yunnan University - South Gate	Chenggong	POINT (586146.480 2746968.095)
4	4	10	Southwest Associated University Research Institute affiliated school - gate 3	Chenggong	POINT (587599.978 2748137.044)

Step 2 Calculation

In the previous step, we have obtained the R value

In this step, we will start from the residential area and find all the emergency shelter entrances within the search radius

The specific formula is as follows:

A i = ∑ f ∈ { d i j ≤ d 0 } R j A_i=\sum_{f\in \{{d_{ij}\le d_0}\}}R_j Ai=f∈{dij≤d0}∑Rj

KM_Poi_c=KM_Poi.copy()

# In consideration of thread optimization, we still make tables
R_N=dict(zip(YJBNS_Ent_c['NAME'],YJBNS_Ent_c['R_val']))

A_list=[]
for i in range(KM_Poi_c.shape[0]):
    name=KM_Poi_c.iloc[i,3]
    points=getData(S2E[name],Threshold)
    # At this time, only R needs to be calculated_ Sum of Val
    ans=0
    for poi  in points:
        # There is still a problem of mismatch
        try:
            ans+=R_N[poi[1]]
        except:
            ans+=0
    A_list.append(ans)

KM_Poi_c['A_val']=A_list
KM_Poi_c.head()

	FID	OBJECTID	osm_id	name	type	population	QUYU_NAME	geometry	A_val
0	0	3	474552927	Guandu Street	town	183624	public ferry	POINT (576290.931 2761828.261)	0.245758
1	1	12	1483174846	Haikou Street	town	69019	Xishan	POINT (561304.355 2742770.016)	0.000000
2	2	14	-1995559001	Majinpu Street	town	54798	Chenggong	POINT (581339.943 2742863.779)	0.000000
3	3	15	-1659466282	Ala Street	town	87545	public ferry	POINT (579586.509 2766116.964)	0.000000
4	5	22	-782694876	Shuanglong Street	town	11841	Panlong	POINT (585541.983 2778974.166)	0.000000

Storage and display

KM_Poi_c.to_file(r"C:\Users\Falling flower rain\Documents\Tencent Files\651421775\FileRecv\New folder\Data\Accessibility.shp")

KM_Poi_c.plot()

The results are as follows:

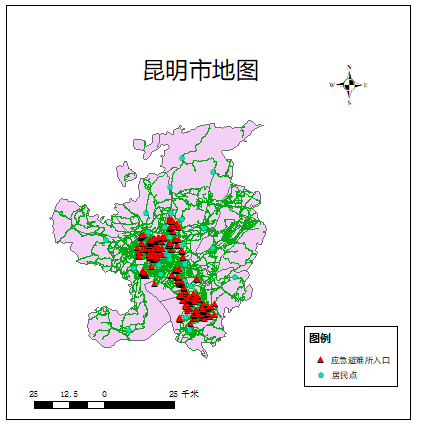
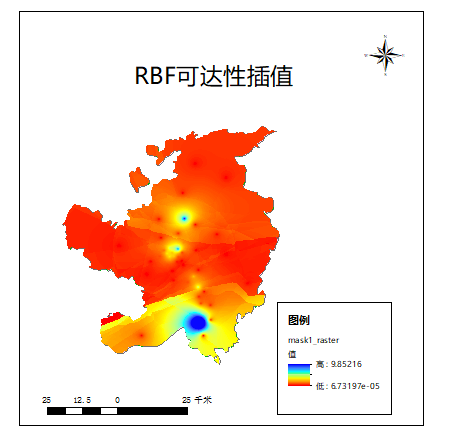
Demo improvements

At present, the improvement directions considered are:

Adaptive search radius
More reasonable Poisson flow damping
More complex human land relationship model
Correctness correction of data source

Keywords: Python gis

Added by phpchamps on Fri, 11 Feb 2022 21:58:12 +0200

Programming VIP