Students who participate in the blue bridge cup can pay attention to the blogger. The blogger is also preparing the Blue Bridge Cup and can brush questions with the blogger's blog.

Blue Bridge Cup

My AcWing

The title and pictures are from the counseling class of group ab of Blue Bridge Cup C + +

Prefix and

When we want to quickly find the sum of all numbers in a certain interval of a static array (which will not be modified in the middle), we can use prefix sum to deal with it.

One dimensional prefix sum

Suppose the interval of an array a is [L, R], and the time complexity of traversing it all is O(N)

for (int i = L; i <= R; i++) {
	res += a[i];
}

If we need to calculate it many times, it may time out, so the prefix sum can quickly let us calculate the sum of all numbers in a certain interval.

Thought:

We preprocess a new array again: s[i]= a[1] + a[2] +... + a[i], s[i] is the sum of the first I numbers of the original array, and the special provision is s[0] = 0; Processing s is fast because we can find s [ i ] = s [ i − 1 ] + a [ i ] ( common type one ) s[i] = s[i - 1] + a[i] (formula I) s[i]=s[i − 1]+a[i] (formula 1) s[i] can be obtained through one cycle:

for (int i = 1; i < n; i++) {
	s[0] = s[i - 1] + a[i];
}

When we have s, we want to calculate the sum of L to R, so we can use s: a [ L ] + a [ L + 1 ] + a [ L + 2 ] + . . . + a [ R ] = s [ R ] − s [ L − 1 ] ( common type two ) a[L] + a[L + 1] + a[L + 2] + ... + a[R] = s[R] - s[L - 1] (formula 2) a[L]+a[L+1]+a[L+2]+...+a[R]=s[R] − s[L − 1] (formula 2)

It can be found that after preprocessing a s, it is very easy for us to calculate the sum of a certain section. We can directly calculate the difference between the two numbers, that is, we can only use one operation every time we calculate the sum, and each query optimizes the time complexity: O ( N ) → O ( 1 ) O(N) → O(1) O(N)→O(1)

2D prefix and

Do we have a formula like one-dimensional prefix sum?

In one dimension, each s[i] of our prefix and array represents the sum of the first I numbers of the original array;

In two dimensions, the number of our prefix and matrix represents the sum of all elements in the upper left corner of the original matrix:

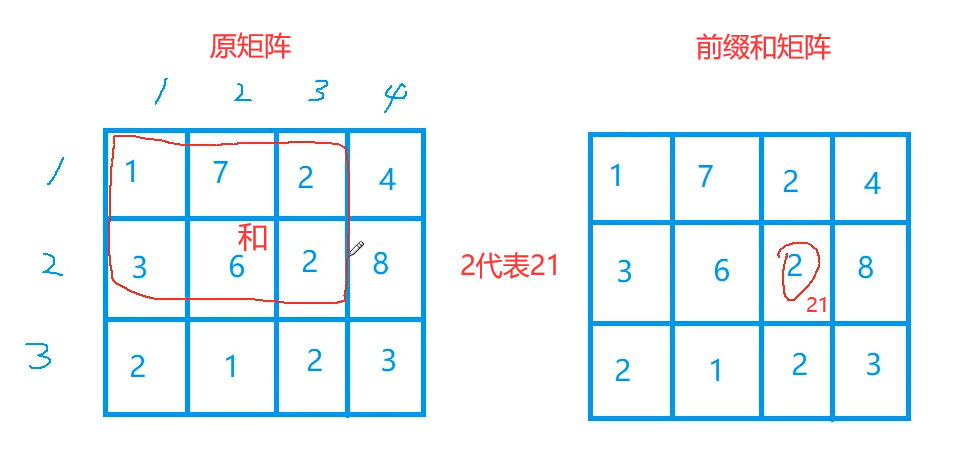
Replace all numbers with prefixes and matrices:

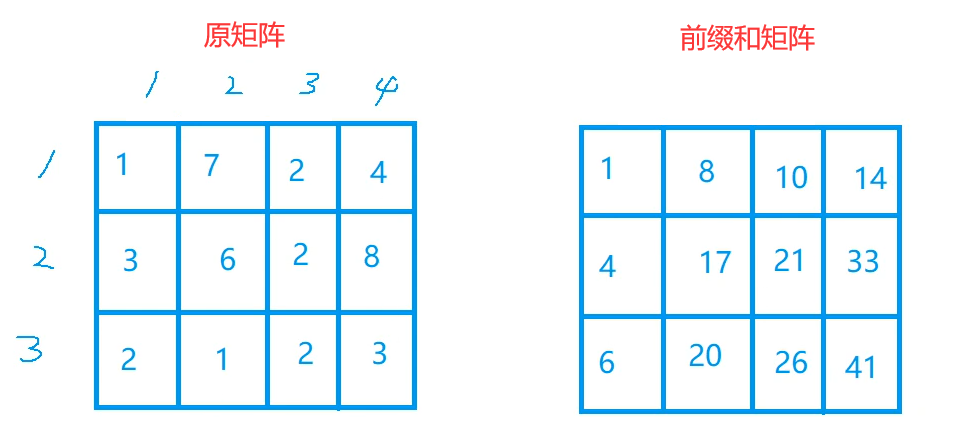
First question: how to calculate the prefix and matrix? How do we calculate it through the original matrix?

Inclusion exclusion principle

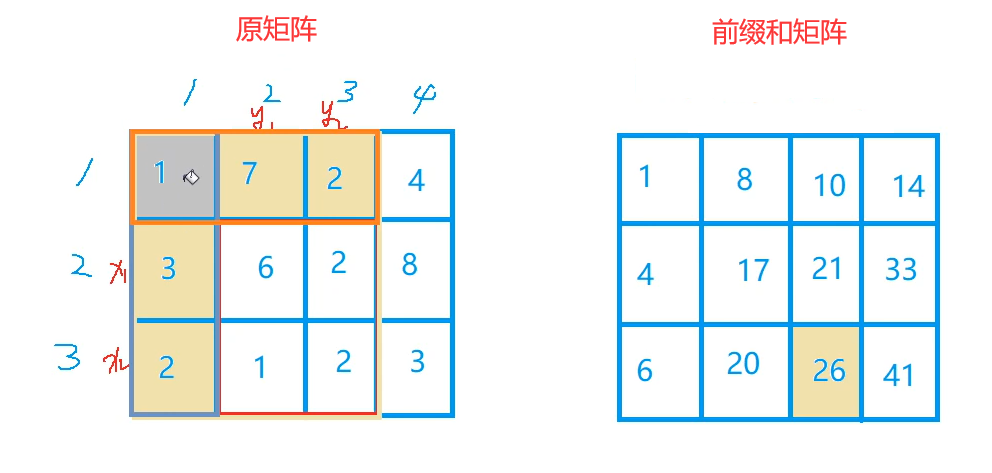
What is the inclusion exclusion principle? Look at the picture:

Our goal is to sum these six numbers:

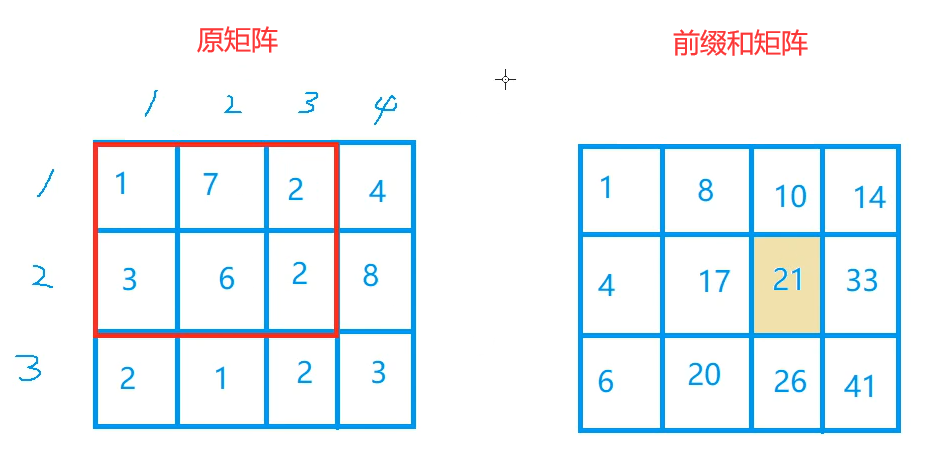
Then we can first find the sum of the four numbers on the left:

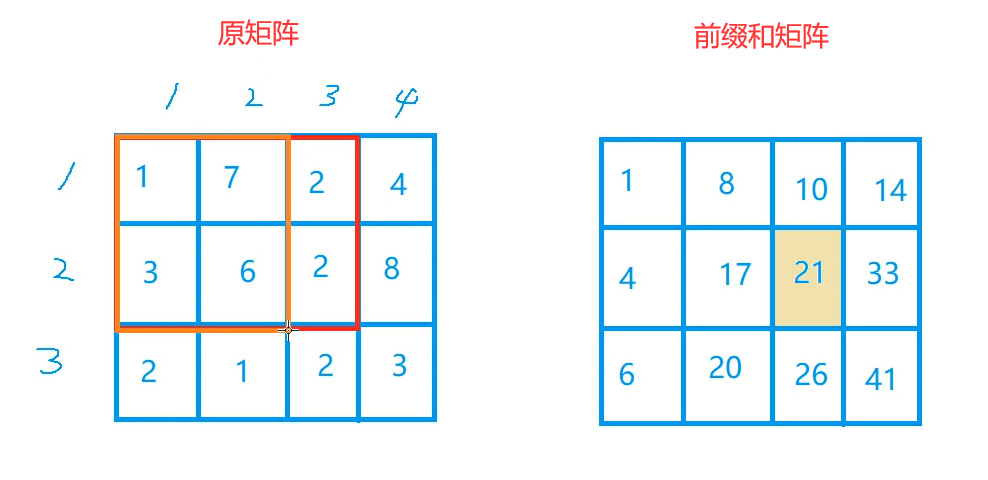
Then sum the above three numbers:

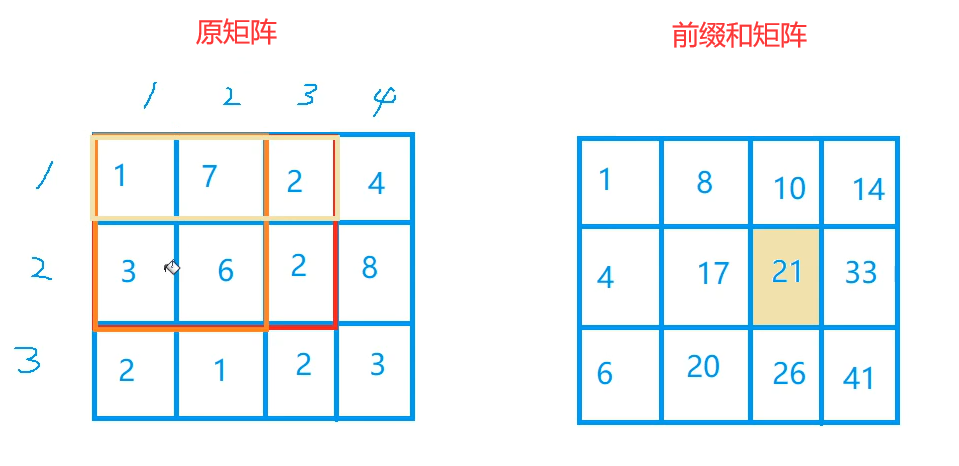
Now the sum is: the Yellow grid is calculated once and the blue grid is calculated twice, so we only need to subtract all the blue grids to ensure that all numbers are added only once except the last grid with its own number, so that we can add this number to get the value of the prefix and matrix.

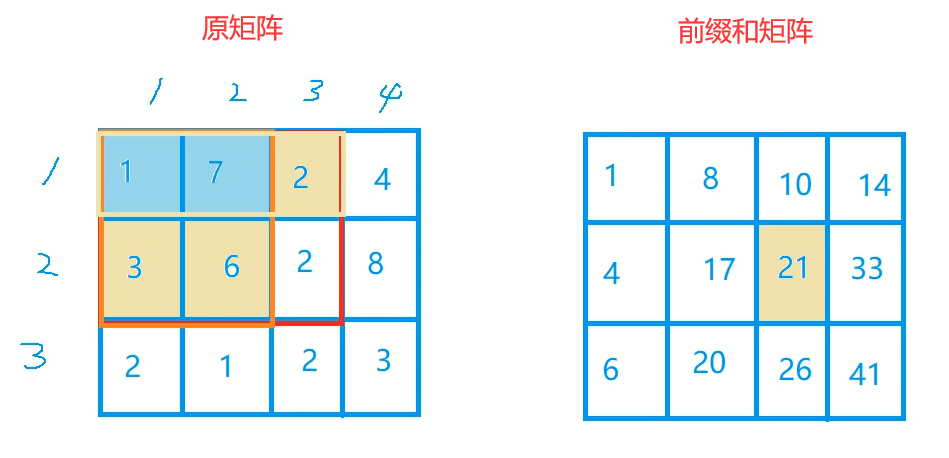
We have summarized that the value of prefix and matrix = the sum of all numbers on the top of this lattice + the sum of all numbers on the left of this lattice - repeated lattice + original number

Namely: s [ x ] [ y ] = s [ x − 1 ] [ y ] + s [ x ] [ y − 1 ] − s [ x − 1 ] [ y − 1 ] + a [ x ] [ y ] ( common type one ) s[x][y] = s[x - 1][y] + s[x][y - 1] - s[x - 1][y - 1] + a[x][y] (formula I) s[x][y]=s[x − 1][y]+s[x][y − 1] − s[x − 1][y − 1]+a[x][y] (formula I)

We can calculate the prefix and the value of the matrix through the original matrix within the linear time complexity. We only use constant times to calculate.

The second question: how to use prefix and matrix to calculate the sum of a sub matrix?

Same: principle of tolerance and exclusion

For example, we want to calculate the sum of the red submatrix in the figure below:

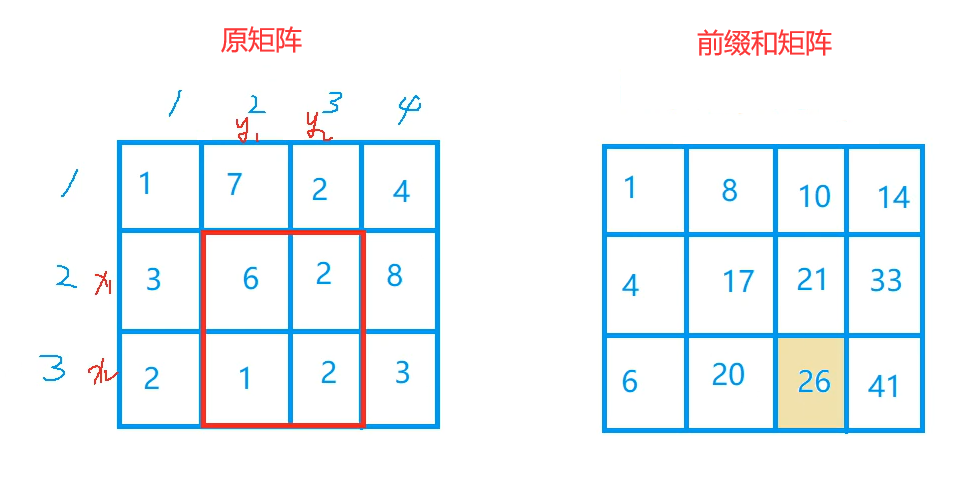
But now we only know the value of the Yellow matrix:

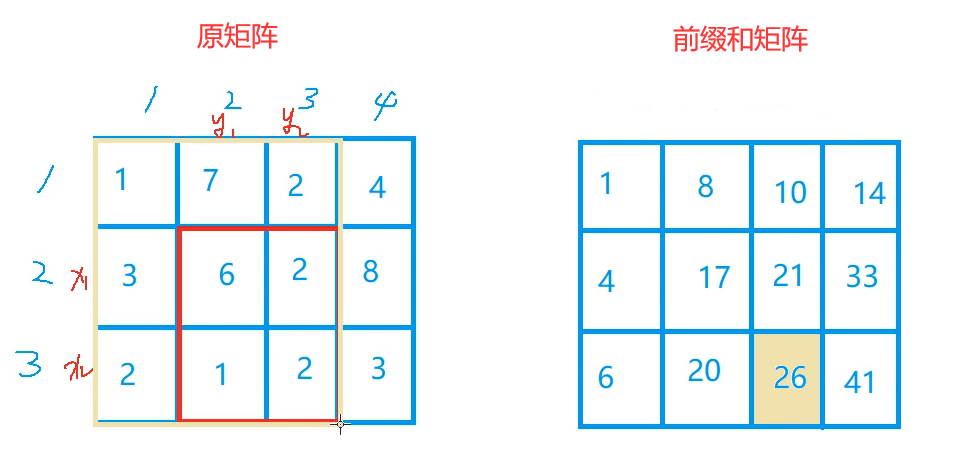
We need to remove the value of the "inverted L" shape, which can be removed by the inclusion exclusion principle. First remove all the values on the left, and then remove the above values;

Now, we have removed all the Yellow grid, but we have removed the gray grid twice, so we have to add it again.

Final formula: the sum of submatrixes with (x1, y1) as the upper left corner and (x2, y2) as the lower right corner is: s [ x 2 , y 2 ] − s [ x 2 , y 1 − 1 ] − s [ x 1 − 1 , y 2 ] + s [ x 1 − 1 , y 1 − 1 ] ( common type two ) s[x2, y2] - s[x2, y1 - 1] - s[x1 - 1, y2] + s[x1 - 1, y1 - 1] (formula 2) s[x2,y2] − s[x2,y1 − 1] − s[x1 − 1,y2]+s[x1 − 1,y1 − 1] (formula 2)

We use the prefix combination matrix to quickly calculate the sum of one of our sub matrices with constant times. The time complexity is optimized as follows: O ( m n ) → O ( 1 ) O(mn) → O(1) O(mn)→O(1)

The two-dimensional prefix sum is mainly an extension of the one-dimensional prefix sum.

The principle of tolerance and exclusion is the concept of exchanging space for time.

The idea of prefix and is very important and will be used in many topics.

Examples

AcWing 795. Prefix and

One dimensional prefix and template questions

Violence takes time for each query O ( n ) O(n) O(n), m times in total, total time complexity O ( m n ) O(mn) O (MN) n, m < = 100000, Mn = 1e10, timeout.

Prefix and optimization, time for each query O ( 1 ) O(1) O(1), m times in total, total O ( n ) O(n) O(n).

Set the template directly.

import java.util.Scanner;

public class Main {
    
    static final int N = 100010;
    static int n, m;
    static int[] a = new int[N]; // Original array
    static int[] s = new int[N]; // Prefix and array are defined as global variables. Array values are all initialized to 0. Separate s[0] = 0 is not required
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
            s[i] = s[i - 1] + a[i]; // Formula 1
        }
        
        while (m-- != 0) {
            int l = sc.nextInt();
            int r = sc.nextInt();
            System.out.println(s[r] - s[l - 1]); // Formula 2
        }
    }
}

AcWing 796. Sum of submatrix

Two dimensional prefix and template questions

Input sample:

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

Output example:

17
27
21

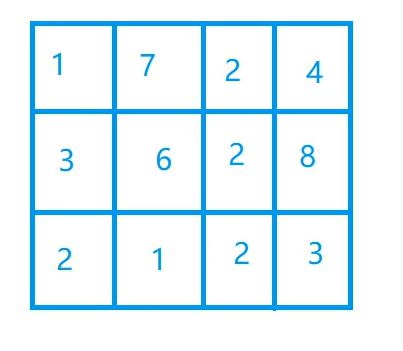
The first two 3, 4 and 3 are the rows and columns of the matrix, and the last 3 is how many times to query

Row 234 is the element of the matrix:

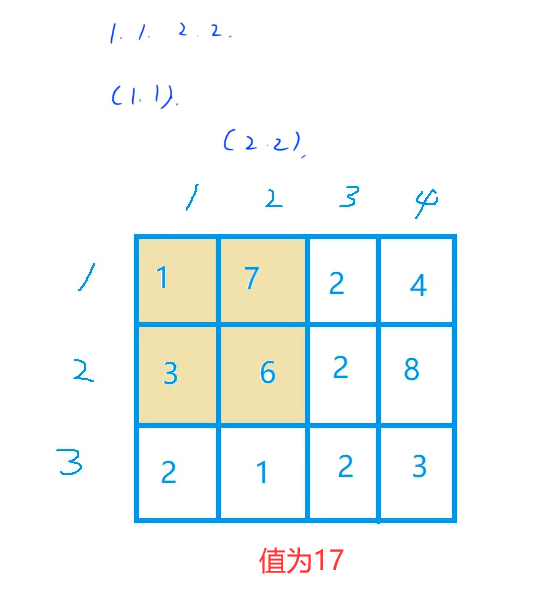
1, 2 and 2 in line 5 are the sum of this submatrix:

2 1 3 4 in line 6 is the sum of this submatrix:

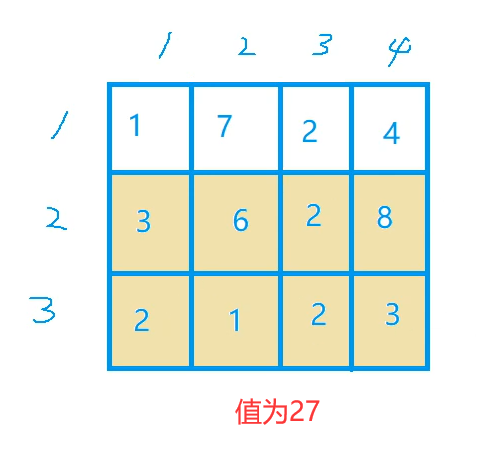
1, 3, 4 in line 7 is the sum of this submatrix:

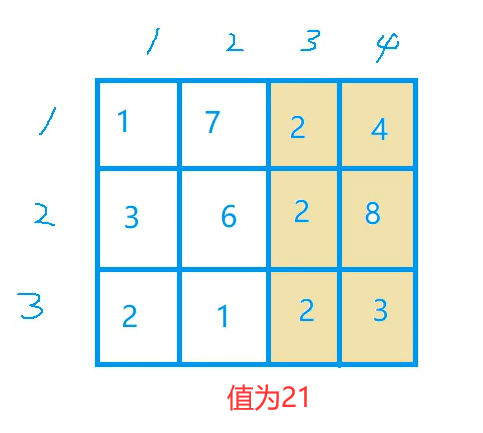
That is to say, this problem is to find the sum of a sub matrix of a matrix.

Then it's ok to write the code directly according to the two-dimensional prefix we talked about earlier. It's already very detailed.

import java.util.Scanner;

public class Main {

    static final int N = 1010;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int q = sc.nextInt();
        int[][] a = new int[N][N];
        int[][] s = new int[N][N];

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                a[i][j] = sc.nextInt();
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; // Formula 1
            }
        }

        while (q-- != 0) {
            int x1 = sc.nextInt();
            int y1 = sc.nextInt();
            int x2 = sc.nextInt();
            int y2 = sc.nextInt();
            System.out.println(s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]); // Formula 2
        }
    }
}

Real topic of the 8th 2017 Blue Bridge Cup

AcWing 1230. K-fold interval

JavaB group question 10

One dimensional prefix sum

A continuous interval is a multiple of k

Let's look at the first example:

Input sample:

5 2
1
2
3
4
5

Output example:

6

Find 5 numbers. How many times is a continuous interval 2

The length is 1:2, 4 2

The length is 2:0

Length is 3: [1,3] [3,5] 2

The length is 4: [1, 4] [2, 5] 2

The length is 5:0

The sum is 6 and the output is 6.

Violent enumeration

The most simple approach

Time complexity O ( N 3 ) O(N^3) O(N3)

Timeout, AcWing only passed 6 / 11 data, Blue Bridge Cup passed 2 / 7 data, out of 100 points, I only got 28 points

import java.util.Scanner;

public class Main {
    
    static final int N = 100010;
    static int[] a = new int[N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int k = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
        }
        int res = 0;
        for (int r = 1; r <= n; r++) { // Right endpoint
            for (int l = 1; l <= r; l++) { // Left endpoint 
                int sum = 0;
                for (int i = l; i <= r; i++) {
                    sum += a[i];
                }
                if (sum % k == 0) res++;
            }
        }
        System.out.print(res);
    }
}

Prefix and optimization

Time complexity O ( N 2 ) O(N^2) O(N2)

But it's useless. AcWing still timed out. The evaluation result of the Blue Bridge Cup is the same as that of the violence enumeration. I thought I could cheat more points, which is very silly

import java.util.Scanner;

public class Main {
    
    static final int N = 100010;
    static int[] a = new int[N]; // Original array
    static int[] s = new int[N]; // Prefix and array
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int k = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
            s[i] = s[i - 1] + a[i]; // Formula 1
        }
        int res = 0;
        for (int r = 1; r <= n; r++) { // Right endpoint
            for (int l = 1; l <= r; l++) { // Left endpoint 
                int sum = s[r] - s[l - 1]; // Formula 2
                if (sum % k == 0) res++;
            }
        }
        System.out.print(res);
    }
}

AcWing evaluation results

Blue Bridge Cup evaluation results

A layer of loop is eliminated with prefix and, but the result we want is not achieved. What else can we optimize?

Prefix and + mathematical optimization

Time complexity O ( N ) O(N) O(N)

We can kill another layer of circulation.

When R is fixed, how many l satisfy (s [R] - s [L - 1])% k = = 0 between 1 and R

This is actually the meaning of our second level cycle. We simply change the cycle conditions:

When R is fixed, how many L satisfy (s [R] - s [L])% k = = 0 between 0 and R - 1 can be converted into: s [R]% k = = s [L]% k

That is, how many S[L] are the same as the remainder of S[R]

We can open a new array, cnt[i], to indicate how many numbers the remainder is I

for(int R = 1; R <= n; R++) {
	res += cnt[s[R] % k];
    cnt[s[R] % k]++;
}

Full code AcWing AC Blue Bridge Cup Full Score

Time complexity O ( N ) O(N) O(N)

import java.util.Scanner;

public class Main {
    
    static final int N = 100010;
    static long[] s = new long[N]; // Prefix and array should be set to long to prevent burst int
    static int[] cnt = new int[N]; // An array of numbers for each remainder 
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int k = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            s[i] = s[i - 1] + sc.nextInt(); // The formula has been put in place one step at a time, and there is no need to save the value of the original array
        }
        long res = 0;
        cnt[0] = 1; // cnt[0] stores the number of numbers equal to 0 in s []. Since s[0] = 0, there is 1 number initially equal to 0, so cnt[0] = 1. See the figure below for details
        for (int r = 1; r <= n; r++) { // Mathematical thought optimization formula II
            /* 
                It is recommended to output the following statement: you can see the number of k-times intervals ending with r
                1 0 --> 1%2=1  0 1 res+0 in front
                2 1 --> 3%2=1  There is a 1 res+1 in front
                3 1 --> 6%2=0  There is 1 0 res+1 in front 
                4 2 --> 10%2=0 There are 2 0 res+2 in front
                5 2 --> 15%2=1 There are 2 1 res+2 in front
            */
            //System.out.println(r + " " + cnt[(int)(s[r] % k)]);
            res += cnt[(int)(s[r] % k)];
            cnt[(int)(s[r] % k)]++; // Number of different remainder of record sequence%k
        }
        System.out.print(res);
    }
}

Why should cnt[0] be assigned a value of 1?

Because our idea is to find two sequences with the same number as the remainder of s [R]% K and s [l]% k, and our prefix and general formula do not include s[0], because its value is 0, which has no meaning in the prefix and, but this problem is meaningful. In the example, the prefix and sequence% k are followed by 1 1 0 0 1. Compared with each other, we can only find four, as shown in the following figure:

Without cnt[0] = 1, the value of res is 4

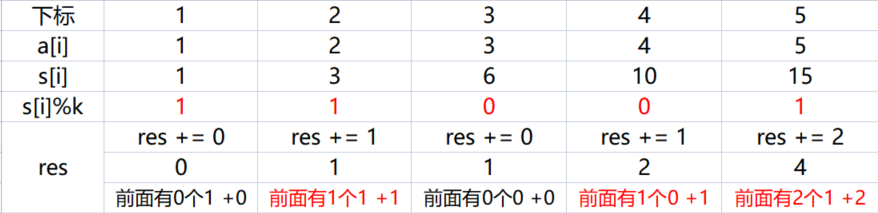
Why are two missing? Because we don't necessarily need two sequences, and the remainder = = 0 of a single sequence also forms a k-fold interval. At this time, we have to assume that s[0] = 0 is meaningful;

What we save in cnt[0] is the number of numbers equal to 0 in s []. Since s[0] = 0, there is 1 number initially equal to 0, so cnt[0] = 1.

Add cnt[0] = 1, and the value of res is 6

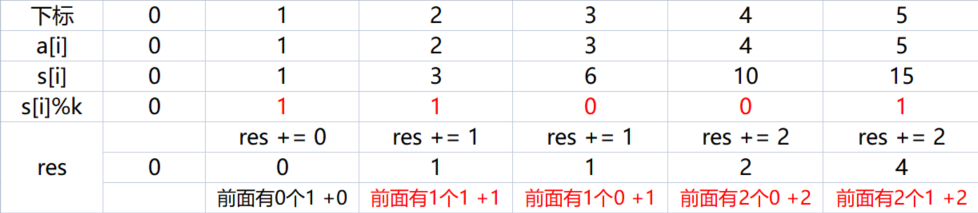
Blue Bridge Cup Full Score

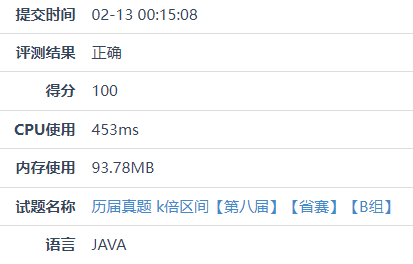
Optimization of this problem: O ( N 3 ) → O ( N 2 ) → O ( N ) O(N^3) → O(N^2) → O(N) O(N3)→O(N2)→O(N)

If you don't understand the code, you can comment below