Data structure and algorithm 2020 notes
1, Linear structure and nonlinear structure
1.1 linear structure (9.17)
Common linear structures: array, queue, linked list, stack
Sequential storage structure (array) and chain storage structure, one-to-one linear relationship
One-to-one array structure, non-linear array structure, non-linear tree structure
1.2 sparse array
When most elements in an array are 0 or an array with the same value, sparse array can be used to save the array
Treatment method:
- How many rows and columns are there in the record array? How many different values are there
- Record the rows, columns and values of elements with different values in a small-scale array, so as to reduce the size of the program (compression)
- Used to preserve two-dimensional arrays (chessboard, map, etc.)
1.3 queue
- Ordered list (array, linked list)
- First in first out
1.3.1 array simulation queue
Disadvantages: cannot be reused
1.3.2 array simulation ring queue
- Conditions for queue full: (rear + 1)% maxSize = front
- Queue is empty: rear == front
- Initial value: front == rear == 0
- Number of valid data in the queue: (rear + maxSize - front)% maxSize (common small algorithm)
1.4 linked list
- Linked list is stored in the form of nodes, chain storage
- Each node contains the data field, and the next field: points to the next node
- The nodes of the linked list are not necessarily stored continuously
- Lead node and headless node. The head node does not store any data and is used to find the linked list entry
//Creation of one-way linked list
private HeroNode head = new HeroNode(0, "");
//Join last
public void add(HeroNode heroNode) {
HeroNode temp = head;
while (true) {
if (temp.next == null) {
break;
}
//If the last is not found, move temp back
temp = temp.next;
}
temp.next = heroNode;
}
//Display linked list (traversal)
public void list(){
if (head.next == null) {
return ;
}
//The head node cannot be moved and needs an auxiliary variable to traverse
HeroNode temp = head.next;
while (true) {
if (temp == null){
break;
}
//syso node
//Move the temp backward and be careful of the dead cycle
temp = temp.next;
}
}
class HeroNode {
public int no;
public String name;
public HeroNode next;
}
/*
Add in order: new nodes next = temp.next; temp.next = new node;
*/
public void addByOrder(HeroNode heroNode){
//Single linked list: the temp to be found is the previous node of the addition location, otherwise it cannot be added
HeroNode temp = head;
boolean flag = false; // Judge whether the added number exists
while (true) {
if (temp.next == null) {
break;
}
if (temp.next.no > heroNode.no) {
break;
} else if (temp.next.no == heroNode.no) {
flag = true;
break;
}
temp = temp.next; // Move back and traverse the current linked list
}
//Judge the value of flag
if (flag) {
//syso exists and cannot be added
} else {
heroNode.next = temp.next;
temp.next = heroNode;
}
}
Modify node \ delete node
public void update(HeroNode heroNode) {
if (head.next == null) {
return;
}
HeroNode temp = new HeroNode();
temp = head;
while (heroNode.no != temp.next.no && temp.next != null) {
update();
temp = temp.next;
}
if (temp.next == null) return;
else update();
}
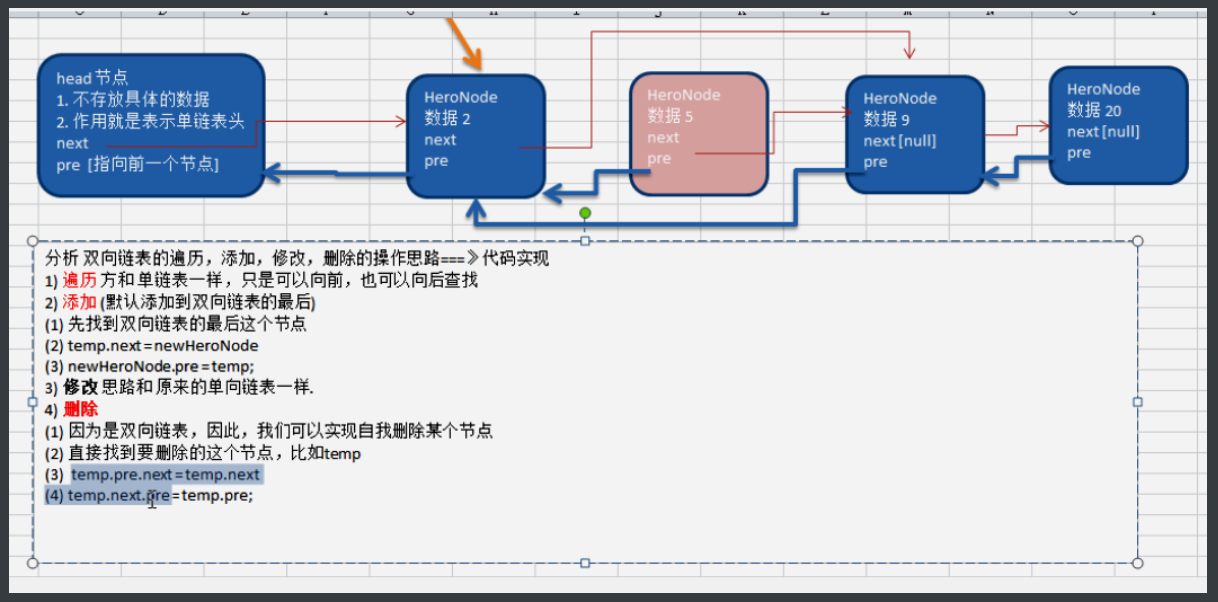
1.4.1 bidirectional linked list
- One way linked list can only be traversed and searched from one direction
- A one-way linked list cannot be deleted by itself and needs to rely on auxiliary nodes, while a two-way linked list can be deleted by itself. When a single linked list deletes a node, you should find temp, which is the previous node of the node to be deleted.
1.5.2 one way circular linked list & Joseph problem
Joseph's problem: let n people with numbers 1, 2,..., n sit around. It is agreed that the person with number k (1 < = k < = n) will count from 1, the person who counts to m will be listed, his next person will start counting, and so on until everyone is listed, resulting in a sequence of out of line numbers.
Solution: circular linked list, array module
public class Josepfu {
public static void main(String[] args){
}
}
class CircleSingleLinkedList{
//first node
private Boy first = new Boy(-1);
public void addBoy(int nums) {
if (nums < 1) {
return;
}
//Use the for loop to create a circular linked list
Boy curBoy = null;
for (int i = 1; i <= nums; i++){
//According to the number, create a child node and an auxiliary node cur
Boy boy = new Boy(i);
if (i == 1) {
first = boy;
first.setNext(first);//Constituent ring
curBoy = first;
} else {
}
}
}
}
//Traverse circular linked list
public void showEle() {
if (first == null) {
return;
}
Boy cur = first;
while (true) {
//syso show cur.no
cur = cur.getNext();
if (cur == first) break;
}
}
class Boy{
private int no ;
private Boy next;
}
Loop out analysis of ring linked list:
- You need to create an auxiliary variable helper to point to the last node of the ring linked list in advance (while loop traversal points to the last node)
- Before counting off, let the first and helper move k-1 times to the location of the K node
- When counting, let the first and helper move m-1 times at the same time
- At this time, circle the child node pointed to by first. First = first next helper. next = first
2, Stack
2.1 introduction to stack
- Ordered list of first in first out
- The top of the stack is the changing end, the insertion and deletion operations, and the bottom of the stack is the fixed end
- Out of stack pop
- Stack push
2.2 application scenarios
- Subroutine calling, processing and recursive calling
- Conversion and evaluation of expressions
- Traversal of binary tree
- Depth first search of graphics
2.3 use of array simulation stack
Train of thought analysis:
- Define a top to represent the top of the stack, which is initialized to - 1,
- Stack operation: Top + +; stack[top] = value;
- Stack out operation: int value = stack[top]; top–; return value;
- When traversing, the data is displayed from the top of the stack
//Judge whether the stack is empty and exit the stack
public int pop() {
if (isEmpty()) {
throw new RuntimeException("Stack empty, no data");
}
int value = stack[top];
top--;
return value;
}
2.4 simulate stack with linked list (null)
3, Prefix, infix, suffix expression
3.1 prefix expression (Polish expression)
- The operator of the prefix expression precedes the operand
- The prefix expression corresponding to (3 + 4) * 5 - 6 is - * + 3 4 5 6
- Computer evaluation method: scan the expression from right to left. When encountering a number, push the number into the stack. When encountering an operator, pop up the two numbers at the top of the stack, use the operator to calculate the corresponding (top element and secondary top element), and put the result into the stack. Repeat the above process until the leftmost end of the expression. The final value is the result of the expression.
- For the above expression, press 6 5 4 3 from right to left, get 7 when encountering + pop 3 4, and then enter the stack when encountering * pop 7 * 5 = 35, 35... At this time, 35 is at the top of the stack
3.2 infix expression
- Is a common operation expression
- However, it is not easy for computers to operate (because infix expressions need to judge the priority of operators and the priority of subsequent operators). When calculating the results, infix expressions are often converted into other expressions (generally suffix expressions)
3.3 suffix expression
- Also known as inverse Polish expression
- Similar to the prefix, except that the operator follows the operand
- (3 + 4) * 5-6: suffix expression: 3 4 + 5 * 6 - 35 is under 6
- 4 * 5 - 8 + 60 + 8 / 2 ------------------- 4 5 * 8 - 60 + 8 2 / +
3.4 inverse Polish calculator (partial code)
//Put the inverse Polish expression, and put the data and operators in sequence, such as 3, 4 + 5 * 6 in ArrayList-
public static List<String> getListString(String str){
String[] split = str.split(" ");
List<String> List = new ArrayList<String>();
for (String ele : split) {
list.add(ele);
}
return list;
}
//calculation
public static int calculate(List<String> ls){
Stack<String> stack = new Stack<String>();
for (String item : ls) {
if (item.matches("\\d+")) {
//Push
stack.push(item);
} else {
//pop out two numbers, operate them, and then put them on the stack
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")){
res = num1 + num2;
} else if (item.equals("-")){
res = num1 - num2;
} else if (item.equals("*")){
res = num1 * num2;
} else if (item.equals("/")){
res = num1 /num2;
} else {
throw new Exception("error");
}
stack.push(res + "");
}
}
return Integer.parseInt(stack.pop());
}
3.5 thinking analysis of infix to suffix expression (9.20)

code:
//Infix expression is converted to the corresponding list, and then infix expression is converted to suffix expression
public static List<String> toInfixExpressionList(String s) {
List<String> ls = new ArrayList<String>();
int i = 0;
String str;
char c;
do {
if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
ls.add("" + c);
i++;
} else {
//If it is a number, multiple numbers need to be considered
str = "";//First set str to "" '0' [48] - > '9' [57]
while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
str += c;
i++;
}
ls.add(str);
}
} while (i < s.length());
return ls;
}
//Infix to suffix
public static List<String> parseSuffixExpressionList(List<String> ls){
//Define two stacks
Stack<String> s1 = new Stack<String>(); //Symbol stack
//Because s2 stack has no pop operation in the whole conversion process, and it needs to be output in reverse order, so list is used
//Stack<String> s2 = new Stack<String>();
List<String> s2 = new ArrayList<String>(); // list2 for storing intermediate results
//Traversal ls
for (String item : ls) {
//If it's a number, add s2
if (item.matches("\\d+")) {
s2.add(item);
} else if (item.equals("(")) {
s1.push(item);
} else if (item.equals(")")) {
while (!s1.peek().equals("(")){
s2.add(s1.pop());
}
s1.pop(); //Pop up(
} else {
while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {
s2.add(s1.pop());
}
s1.push(item);
}
}
//Pop the operators in the remaining s1 into s2 in turn
while (s1.size() != 0) {
s2.add(s1.pop());
}
return s2;
}
//Writing an Operation class can return the priority corresponding to an operator
class Operation{
private static int ADD = 1;
private static int SUB = 1;
private static int MUL = 2;
private static int DIV = 2;
public static int getValue(String operation){
int result = 0;
switch (operation) {
case "+" :
result = ADD;
break;
case "-" :
result = SUB;
break;
case "*" :
result = MUL;
break;
case "/" :
result = DIV;
break;
default :
//syso : not exsist;
break;
}
return result;
}
}
4, Recursion
4.1 application scenario & problem solving
recursion: maze problem (backtracking), printing problem, factorial problem
Problem solving: eight queens problem, Hanoi Tower, factorial, maze, ball and basket, fast row, merge sort, binary search, divide and conquer algorithm, shortest path, minimum spanning tree, problems solved by stack, etc
Call rule:
- When the program executes a method, it will open up an independent space (stack)
- The local variables of the method are independent and will not affect each other
- Reference type variables (in the stack) will share data (such as arrays)
- return end method
4.2 maze problem
4.3 eight queens problem
A typical case of backtracking algorithm: eight queens are placed on an 8 * 8 grid chess. Any two queens cannot be in the same row, column, or slash. Ask how many pendulum methods there are.
92 species
4.3.1 array solution
The number of backtracking reaches 1w5, which is relatively large
//Write a method to place the n th queen
private void check(int n) {
if (n == max) {//max = 8
print();
return;
}
for (int i = 0; i < max; i++) {
//First, put the current queen n in the first column of the row
array[n] = i;
//Judge whether there is a conflict when the nth queen is currently placed in column i
if (judge(n)) {
//No conflict, then put n+1 queens and start recursion
check(n+1); //
}
//If there is a conflict, continue to execute array[n] = i; That is, the nth queen is placed in the backward position of the line
}
}
//Judge whether the placed queen conflicts with the position in front
private boolean judge(int n) {
for (int i = 0; i < n; i ++) { // Growth by line
// 1.array[i] == array[n] means to judge whether the nth queen is in the same column as the previous queen
// 2.Math.abs(n-i) == Math.abs(array[n] - array[i]) determines whether the nth queen is on the same slash as the ith queen
if (array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
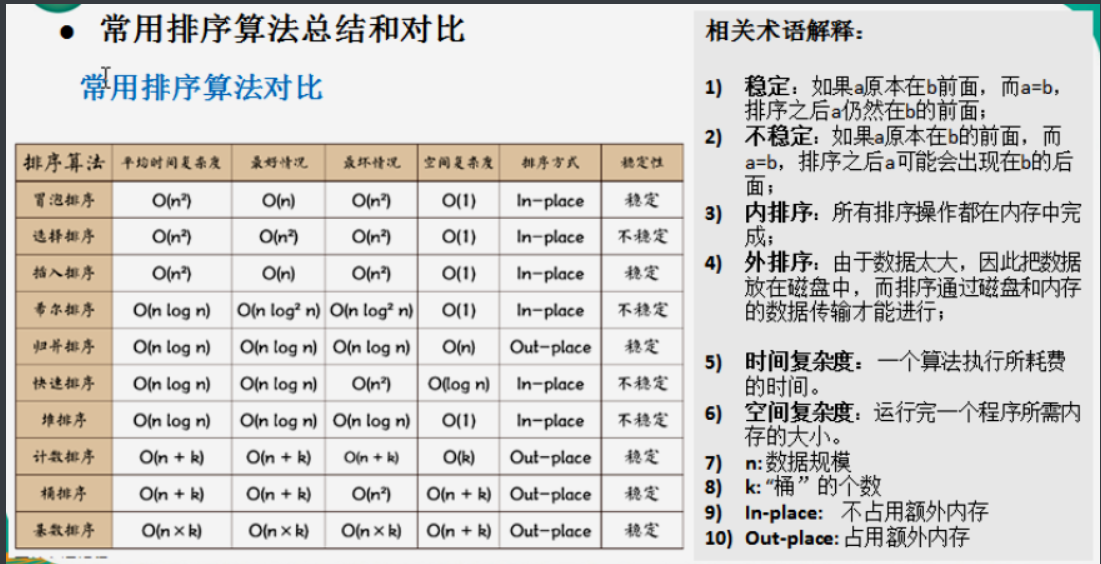
5, Sorting algorithm
5.1 classification of sorting
- Internal sorting (all sorting operations are completed in memory)
: load all data to be processed into internal memory for sorting
: insert sort (direct insert sort, Hill sort), select sort (simple select sort, heap sort), exchange sort (bubble sort, quick sort)
, merge sort, cardinal sort - External sorting method (put data on disk and sort through disk and memory transmission)
5.2 time complexity
Ex post statistical method and ex ante estimation method
5.2.1 time and frequency
The number of statements executed in an algorithm is called statement frequency or time frequency, which is recorded as T(n)
- Ignore constant term: T(n) = 2n = 2n + 10
- Ignore the lower order: T(n^2) = n^2 + 5n + 10 = 3n ^2, perform curve coincidence
- The coefficients of higher-order terms can be ignored. n^3+5n and 6n^3 + 4n, perform curve separation, and explain how much power is the key
5.2.2 calculation of time complexity
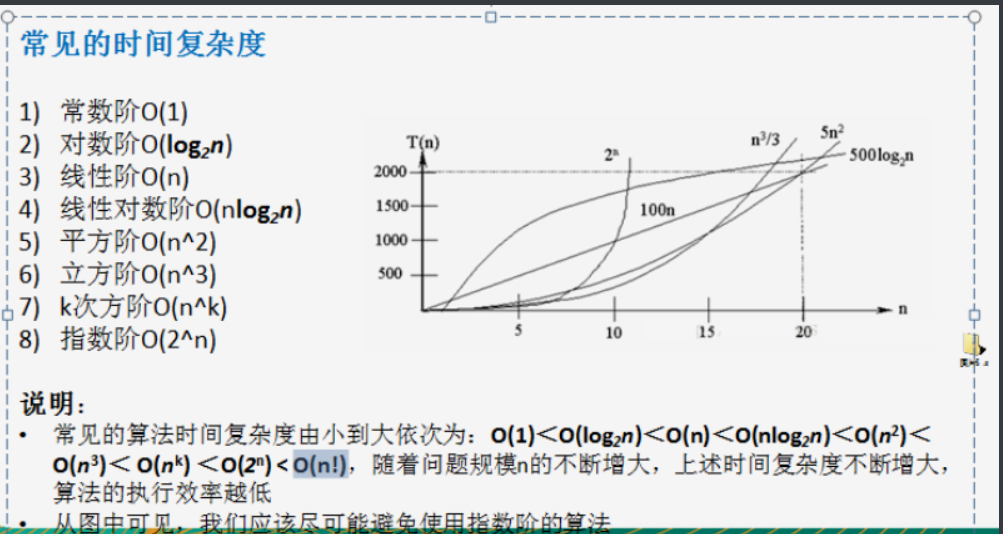
5.2.3 common time complexity
- Constant order O(1): no matter how many lines of code are executed, as long as there is no complex structure such as loop, the time complexity of this code is O(1); (code execution does not increase with the growth of a variable)
- O(logN):
- Linear order O(n):
- Linear order (nlogo):
- ...
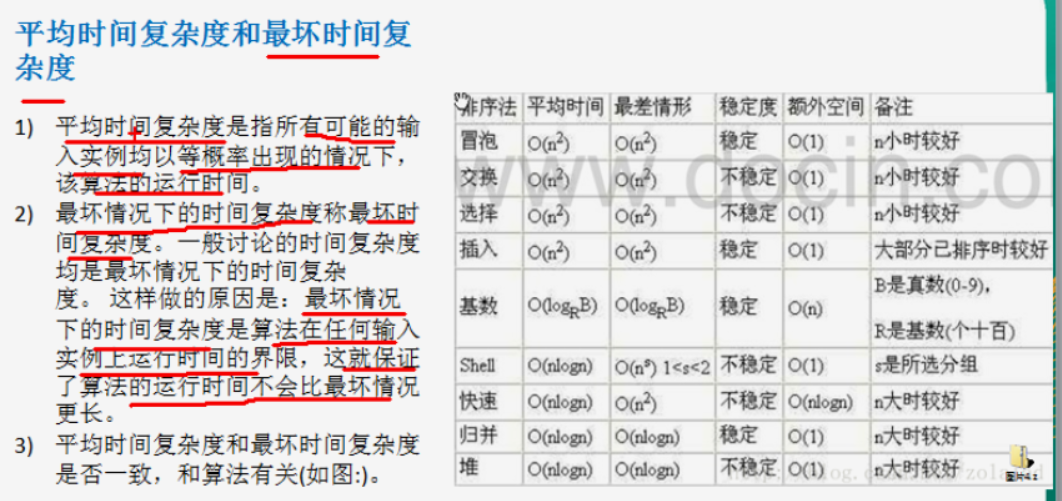
5.2.4 average time complexity and worst time complexity
5.2.5 space complexity
A measure of the amount of storage space temporarily occupied by an algorithm during operation. The essence of some cache products and algorithms (cardinality sorting, fast sorting and merging) is to trade space for time.
5.3 bubble sorting (9.21)
- A total of - 1 cycles of array size are carried out, and the maximum number is ranked last in each sorting
- The number of sortings per trip is gradually decreasing
- If there is no exchange in a certain sort, the bubble sort can be ended in advance. (optimized)
//O(n^2)
public void BubbleSort(int[] arr){
int temp = 0;
boolean flag = false;//Identify variables and whether they have been exchanged for simple optimization
for (int i = arr.length - 1; i >= 0; i--){
for (int j = 0; j < i; j++){
if (arr[j] > arr[j + 1]) {
flag = true;
temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
if(!flag){
break;
} else {
flag = false;
}
}
//for (int i = 0; i < arr.length-1; i++)
// for (int j = 0; j < arr.length - 1 - i; j++){}
}
5.4 selection and sorting
Select the value of the specified size, put it into the specified position according to certain rules, and get the sequence from small to large by traversing n-1 times
First simple and then complex, the complex algorithm is divided into simple problems and then integrated
//Faster than bubble sorting in time
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length -1; i++){
int minIndex = i;
int min = arr[i];
for (int j = i; j < arr.length - 1; j++){
if (arr[j] < min) {
minIndex = j;
min = arr[j];
}
}
if (minIndex != i){
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
5.5 insert sort
Basic idea: regard the n elements to be sorted as an ordered table and an unordered table, take out the first element from the unordered table each time, and insert it into the appropriate position of the ordered table.
public static void InsertSort(int[] arr){
for (int i = 1; i < arr.length; i++){
int insertVal = arr[i];
int insertIndex = i - 1; //The number to be inserted into the unordered list is compared with the previous subscript
//Find the insertion position for insertVal
/*
1.insertVal >= 0, Prevent cross-border
2.insertVal < arr[insertIndex] compare
3.arr[insertIndex] Move back
*/
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
//if (insertIndex+1 == i)
arr[insertIndex + 1] = insertVal;
}
}
5.6 Hill sorting
Possible problems with simple insertion sorting:
When the number of inserts is small, the number of backward moves increases significantly, and the efficiency will be affected
Hill sorting introduction: reduce incremental sorting and insert an efficient version of sorting
Basic idea: group according to a certain increment of subscript, and use insertion sorting for each group. As the increment decreases, it decreases to 1
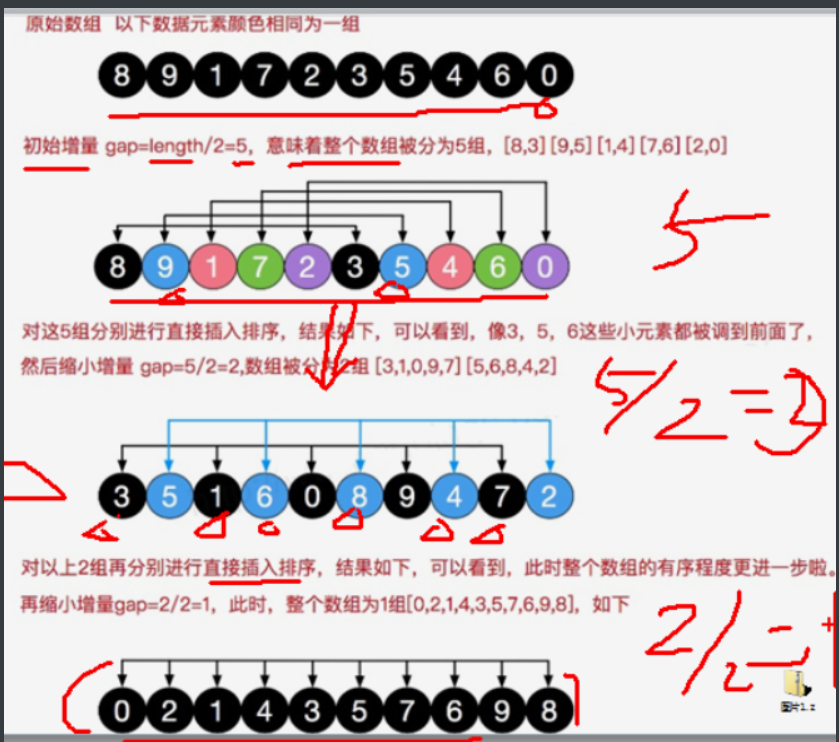
5.6.1 exchange method
public static void shellSort(int[] arr){
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++){
//Traverse all elements in each group (a total of gap groups, each group has), step gap
for (int j = i - gap; j >= 0; j -= gap) {
if (arr[j] > arr[j + gap]){
temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
}
}
}
}
//Low efficiency
}
5.6.2 displacement method
//nlogn - n ^ (1~2)
//Optimize the Hill sort of exchange
public static void shellSort2(int[] arr) {
//Incremental gap
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++){
int j = i;
int temp = arr[j];
if (arr[j] < arr[j - gap]){
while (j - gap >= 0 && temp < arr[j - gap]) {
//move
arr[j] = arr[j - gap];
j -= gap;
}
//After exiting the while loop, explain to find the insertion location for temp
arr[j] = temp;
}
}
}
}
5.7 quick sort
Basic idea: an improvement of bubble sorting. Through one-time sorting, the data to be sorted is divided into two independent parts. All the data in one part is smaller than all the data in the other part, and then the two parts are sorted quickly, which can be carried out in the same recursive way, so as to make the whole data orderly.
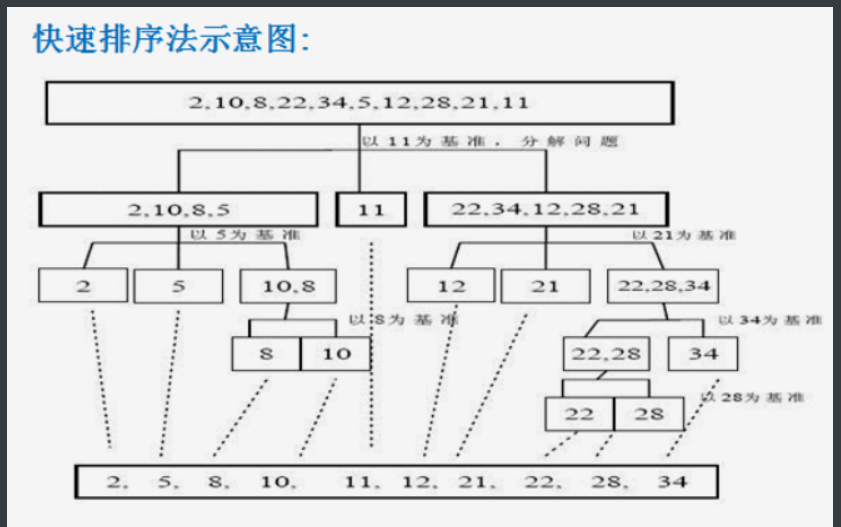
Code implementation:
//Recursive implementation of nlogn - n^2 recursion uses the stack to open up space and change space for time
public static void quickSort(int[] arr, int left, int right) {
int l = left;
int r = right;
//Central axis value
int pivot = arr[(left + right) / 2];
int temp = 0;
//The purpose of the while loop is to put those smaller than the pivot value on the left and those larger on the right
while ( l < r ){
//Keep looking on the left of pivot
while (arr[l] < pivot) {
l += 1;
}
while (arr[r] > pivot) {
r -= 1;
}
if (l >= r) {
break;
}
//exchange
temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//If after the exchange, it is found that arr [l] = = the value of pivot, equal r --, move forward and reach the median value, stop the cycle
if (arr[l] == pivot) r -= 1;
if (arr[r] == pivot) l += 1;
}
//If l == r, it must be L + +, r --, otherwise the stack overflows
if (l == r) {
l+= 1;
r-= 1;
}
if (left < r) quickSort(arr, left, r);
if (right > l) quickSort(arr, l, right);
}
5.8 merge sort
Merge sort, using divide and conquer strategy
Rule: merge two ordered subsequences into one ordered sequence,
mergeSort: O(nlogN)
public static void mergeSort(int[] arr, int left, int mid, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2;
//Decompose recursively to the left
mergeSort(arr, left, mid, temp);
//right
mergeSort(arr, mid + 1, right, temp);
// To merge
merge(arr, left, mid, right, temp);
}
}
public static void merge(int[] arr, int left, int mid, int right, int[] temp){
int i = left;
int j = mid + 1;
int t = 0; // Current index to temp
//First fill the left and right (ordered) data into the temp array until one side is processed
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]){
temp[t] = arr[i];
t += 1;
i += 1;
} else {
temp[t] = arr[j];
t += 1;
j += 1;
}
}
//Fill remaining
while (i <= mid) {
//Left remaining
temp[t] = arr[i];
t+=1;
i+=1;
}
while (j <= right){
temp[t] = arr[j];
t+=1;
j+=1;
}
//Copy the elements of temp array to arr
t = 0;
int tempLeft = left;
while (tempLeft <= right) {
// Merge 0, 1, 2, 3, 0, 3 for the first time.
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
5.9 cardinality sorting (bucket sorting extension)
- The elements to be sorted are assigned to some buckets by the value of each bit of the key value
- Cardinality sorting is an extension of bucket sorting
- Invented by Herman hollery in 1887: the integer is cut into different numbers according to the number of digits, and then compared according to each digit
- Stability ranking: 3 1 4 1 "1 1 3 4, the first 1 is still in the front
- Basic idea: unify all the values to be compared into the same digit length, fill zero in front of the number with shorter digits, and then sort them successively from the lowest bit.

public static void radixSort(int[] arr) {
//Define a two-dimensional array, representing 10 buckets, and each bucket is a one-dimensional array
//Cardinality sorting: the classical operation of space for time
int[][] bucket = new int[10][arr.length];
//In order to record how many data are actually stored in each bucket, a one-dimensional array is defined to record the number of data put in each bucket
//For example, bucketElementCounts[0] records the number of data put into the bucket[0]
int[] bucketElementCounts = new int[10];
//The first round of sorting is to sort the bits of each element
for (int j = 0; j < arr.length; j++) {
//Take out the single digit of each element
int digitOfElement = arr[j] / 1 % 10;
//Put it into the corresponding bucket
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//According to the order of this bucket (the subscript of one-dimensional array takes out the data in turn and puts it into the original array)
int index = 0;
//Traverse each bucket and put the data in the bucket into the original array
for (int k = 0; k < bucketElementCounts.length; k++){
//Judge whether there is data in the bucket
if (bucketElementCounts[k] != 0) {
//
for (int l = 0; l < bucketElementCounts[k]; l++){
arr[index++] = bucket[k][l]; //++
}
}
//After the first round of processing, bucketelementcounts [k] = 0, the bucket array needs to be emptied
bucketElementCounts[k] = 0;
}
//***********First round*************************
//The second round: take ten arr[j] / 10% 10; 748 / 10 > 74 % 10 > 4
}
public static void radixSort2(int[] arr) {
//Final code
//1. Get the maximum number of digits in the array
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
int[][] bucket = new int[10][arr.length];
//What is the maximum number
int maxLength = (max + "").length();
int[] bucketElementCounts = new int[10];
for (int i = 0, n = 1; i < maxLength; i++, n *= 10){
//Sort the corresponding bits of each element, including single bit, ten bit
for (int j = 0; j < arr.length; j++) {
int digitOfElement = arr[j] / n % 10; //** n **
//Put it into the corresponding bucket
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//According to the order of this bucket (the subscript of one-dimensional array takes out the data in turn and puts it into the original array)
int index = 0;
//Traverse each bucket and put the data in the bucket into the original array
for (int k = 0; k < bucketElementCounts.length; k++){
//Judge whether there is data in the bucket
if (bucketElementCounts[k] != 0) {
//
for (int l = 0; l < bucketElementCounts[k]; l++){
arr[index++] = bucket[k][l]; //++
}
}
//After the first round of processing, bucketelementcounts [k] = 0, the bucket array needs to be emptied
bucketElementCounts[k] = 0;
}
}
}
matters needing attention:
- The amount of data is too large, resulting in heap memory overflow
- Negative numbers cannot be sorted directly. If you want to deal with negative numbers, you need to improve.
6, Search algorithm (9.22)
- Sequential (linear) lookup
- Binary search
- Interpolation search
- fibonacci search
6.1 binary search
Binary search needs to find an ordered array
public static int binarySearch(int[] arr, int left, int right, int findVal){
//Not found, end recursion
if (left > right> return -1;
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) {
return binarySearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) {
return binarySearch(arr, left, mid - 1, findVal);
} else {
return mid;
/*
Add an index that returns all the same values
List<Integer> resIndexList = new ArrayList<Integer>();
int temp = mid - 1;
while (true){
if (temp < 0 || arr[temp] != findVal) {break;}
resIndexlist.add(temp);
temp -= 1;
//temp Shift left
}
resIndexlist.add(mid);
//Scan right
temp = mid + 1;
while (true){
if (temp > arr.length - 1 || arr[temp] != findVal) {break;}
resIndexlist.add(temp);
temp += 1;
//temp Shift right
}
return resIndexlist
*/
}
}
6.2 interpolation search

//Write interpolation search algorithm (sequence order is required)
public static int insertValueSearch(int[] arr, int left, int right, int findVal) {
if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) return -1;
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midVal = arr[mid];
if (findVal > midVal) {
return insertValueSearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) {
return insertValueSearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
//Note: for the look-up table with large amount of data and uniform keyword distribution, interpolation search is faster
//Uneven (great jumping), not necessarily better than two points
6.3 Fibonacci (golden section) search algorithm
- Golden section point: a line segment is divided into two parts. The ratio of one part to the whole length is equal to that of the other part, with an approximate value of 0.618
- The ratio of two adjacent numbers in Fibonacci sequence is infinitely close to the golden section value of 0.618
//To create a Fibonacci sequence non recursively, you need to create a Fibonacci sequence first
public static int[] fib(){
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++){
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
//If the length of Fibonacci is not enough by using non recursion, it needs to be supplemented
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0;//Subscript representing the Fibonacci division value
int mid = 0;
int f[] = fib();
//Get k
while(high > f[k] - 1) {
k++;
}
//Because the value of f[k] may be greater than the length of a, we need to construct a new array
int[] temp = Arrays.copyOf(a, f[k]);
for (int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
//Use the while loop to find the key
while (low <= high) {
mid = low + f[k - 1] - 1;
if (key < temp[mid]) {
//Find left
high = mid - 1;
k--;
} else if (key > temp[mid]) {
//Find right
low = mid + 1;
//f[k] = f[k-1] + f[k-2]; So we continue the segmentation from the part of F [K-2]
k -= 2;
} else {
//When you find it, make sure to put the subscript back
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
}
7, Hash table
java program > cache products (redis, memcache) / hash table (array + linked list, array + binary tree) > L2 cache > Database
Hash table: (hash table), a data structure accessed according to the key value. Records are accessed by mapping the key value to a position in the table to speed up the search. This mapping function is called hash function, and the array storing records is called Hash list.
Manage employee information with hash table:
public class HashTabDemo{
}
//Create hashTab to manage multiple linked lists
class HashTab{
private EmpListedList[] empLinkedListArray;
private int size;
//
public HashTab(int size) {
this.size = size;
empLinkedListArray = new EmpLinkedList[size];
//
}
//Add employee
public void add(Emp emp) {
//According to the employee's id, get the linked list to which the employee should be added
int empLinkedListNo = hashFun(emp.id);
empLinkedListArray[empLinkedListNo].add(emp);
}
//Traverse all linked lists
public void list(){
for (int i = 0; i < size; i++) {
empLinkedListArray[i].list();
}
}
//Hash function, using simple modular method
public int hashFun(int id) {
return id % size;
}
//Find the employee based on the entered id
public void findEmpById(int id){
int empLinkedListNo = hashFun(id);
Emp emp = empLinkedListArray[empLinkedListNo].findeEmpById(id);
if (emp == null) {} else {}
}
}
class Emp{
public int id;
public String name;
public Emp next;
public Emp(){
}
}
class EmpLinkedList{
//Header pointer, execute the first emp
private Emp head;
//Add employee to linked list
public void add(Emp emp) {
if (head == null) {
head = emp;
return;
}
//Not the first, use the auxiliary pointer to locate the last
Emp curEmp = head;
while(true) {
if (curEmp.next == null) {
break;
}
curEmp = curEmp.next;
}
curEmp.next = emp;
}
//Employee information traversing the linked list
public void list(){
if (head == null) {
return;
}
Emp cuEmp = head;
while (true){
//syso id\name
if(curEmp.next == null) break;
curEmp = curEmp.next;
}
}
//Find employees by id
public Emp findEmpById(int id) {
//Determine whether the linked list is empty
if (head == null) {
return null;
}
//Auxiliary pointer
Emp curEmp = head;
while (true) {
if (curEmp.id == id) {
break;
}
if (curEmp.next == null){
curEmp = null;
break;
}
curEmp = curEmp.next;
}
return curEmp;
}
}
8, Tree
8.1 Foundation (r1 9.26)

8.2 binary tree
- A tree with up to two child nodes per node
- Child nodes are divided into left nodes and right nodes
- If all leaf nodes of the binary tree are in the last layer, and the total number of nodes = 2^n-1,n is the number of layers, which is called full binary tree
- If all leaf nodes of the binary tree are in the last or penultimate layer, and the leaf nodes of the last layer are continuous on the left and the leaf nodes of the penultimate layer are continuous on the right, it is called a complete binary tree.
- According to the output of the parent node, traversal is divided into the first, middle and last three types. Pre order traversal: first output the parent node, left subtree, right subtree, and so on.
public class BinaryTreeDemo {
main{
}
}
//Define BinaryTree binary tree
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root){
this.root = root;
}
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else //syso null
{}
}
public void infixOrder() {
}
//Postorder traversal
public void postOrder(){
}
}
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
super();
this.no = no;
this.name = name;
}
//get set
//toString
//Write preorder traversal
public void preOrder() {
//syso this
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
//Middle order traversal
public void infixOrder(){
if (this.left != null){
this.left.infixOrder();
}
//syso this
if (this.right != null){
this.right.infixOrder();
}
}
//Postorder traversal
public void postOrder(){
if (this.left != null){
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
//syso this
}
}
8.2.1 binary tree - find the specified node
//Preorder traversal
public HeroNode preOrderSearch(int no) {
if (root != null) return root.postOrderSearch(no);
else return null;
}
//Preorder traversal search
public HeroNode preOrdersearch(int no) {
//Compare whether the current node is
if (this.no == no) {
return this;
}
//Then judge whether the left child node of the current node is empty. If not, recursive preorder search
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.preOrderesearch(no);
}
if (resNode != null) return resNode;
//1. Left recursive preorder search
//2. Right
if (this.right != null) resNode = this.right.preOrdersearch(no);
return resNode;
}
8.2.2 deleting nodes
//Simple requirements: 1 Directly delete leaf nodes, 2 Delete subtree for non leaf node
//Idea: 1 Because the binary tree is one-way, we judge whether the child nodes of the current node need to be deleted, rather than whether the node needs to be deleted
//Because the parent node cannot be found directly
//2 consider whether it is an empty tree root or just one root node
//binaryTree
public void delNode(int no) {
if (root != null) {
if (root.getNo() == no) {
root = null;
}else {
root.delNode(no);
}
} else {
//syso null
}
}
//Recursively delete nodes
public void delNode(int no) {
if (this.left != null && this.left.no == no) {
this.left = null;
return;
}
if (this.right != null && this.right.no == no){
this.right = null;
return;
}
if (this.left != null) {
this.left.delNode(no);
}
if (this.right != null) {
this.right.delNode(no);
}
}
Binary tree storage order
Basic description: from the perspective of data storage, the storage mode of array and tree can be converted to each other.
characteristic:
- Sequential binary trees usually only consider complete binary trees
- The left child node of the nth element is 2 * n + 1; The right child node is 2 * n + 2; Parent node is (n - 1) / 2
class ArrBinaryTree{
private int[] arr;// An array that stores data nodes
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
public void preOrder(){
this.preOrder(0);
}
//Write a method to complete the preorder traversal of the sequential storage binary tree
public void preOrder(int index) {
//If the array is empty, or arr.length = 0
if (arr == null || arr.length == 0)
//syso is null
if (index * 2 + 1 < arr.length) {
preOrder(2 * index + 1);
}
//Right recursive traversal
if ((index * 2 + 2) < arr.length) {
}
}
}
8.4 cued binary tree (9.23)
Basic introduction:
- The binary list of N nodes contains n + 1 (2n - (n - 1) = n + 1) empty finger fields. The null pointer field in the binary linked list is used to store the pointer to the predecessor and successor nodes of the node in a certain traversal order (this additional pointer is called clue)
- Clue linked list, clue binary tree, pre order clue binary tree, middle order clue binary tree, post order
- Precursor node: the previous node of a node
//Medium order cued subtree
public void threadedNodes(HeroNode node) {
//If node == null, it cannot be threaded
if (node == null) return;
//1. Cued left subtree
threadedNodes(node.getLeft());
//2. Cue the current node
//Process the precursor node of the current node
if (node.getLeft() == null) {
//Make the left pointer of the current node point to the predecessor node
node.setLeft(pre);
//The pointer to the current node type is modified to the left
node.setLeftType(1);
}
//Process the successor nodes of the current node
//When the node moves to the next node, the point (pre) of the previous node of the node connects the successor to the node
if (pre != null && pre.getRight() == null) {
pre.setRight(node);
pre.setRightType(1);
}
//*****After each node is processed, let the current node be the precursor node of the next node
pre = node;
//3. Cued right subtree
threadedNodes(node.getRight());
}
8.4.1 traversing cued binary tree
Traverse the binary tree with medium order cueing
Analysis: after cueing, the direction of each node changes, so the original traversal method cannot be used. Each node can be traversed by linear method without recursion, which also improves the efficiency of traversal. The order of traversal should be consistent with that of middle order traversal.
//Method of traversing cued binary tree
public void threadedList() {
HeroNode node = root;
while (node != null) {
while (node.getLeftType() == 0){
node = node.getLeft();
}
//syso this node
while (root.getRightType == 1) {
//Gets the successor node of the current node
node = node.getRight();
//syso node
}
//Replace traversed nodes
node = node.getRight();
}
}
8.5 heap sorting (r1)
- Select sort, unstable sort, complexity O(nlogn)

- Generally, large top pile is used in ascending order and small top pile is used in descending order
- By using the operation of large top heap and small top heap for the array
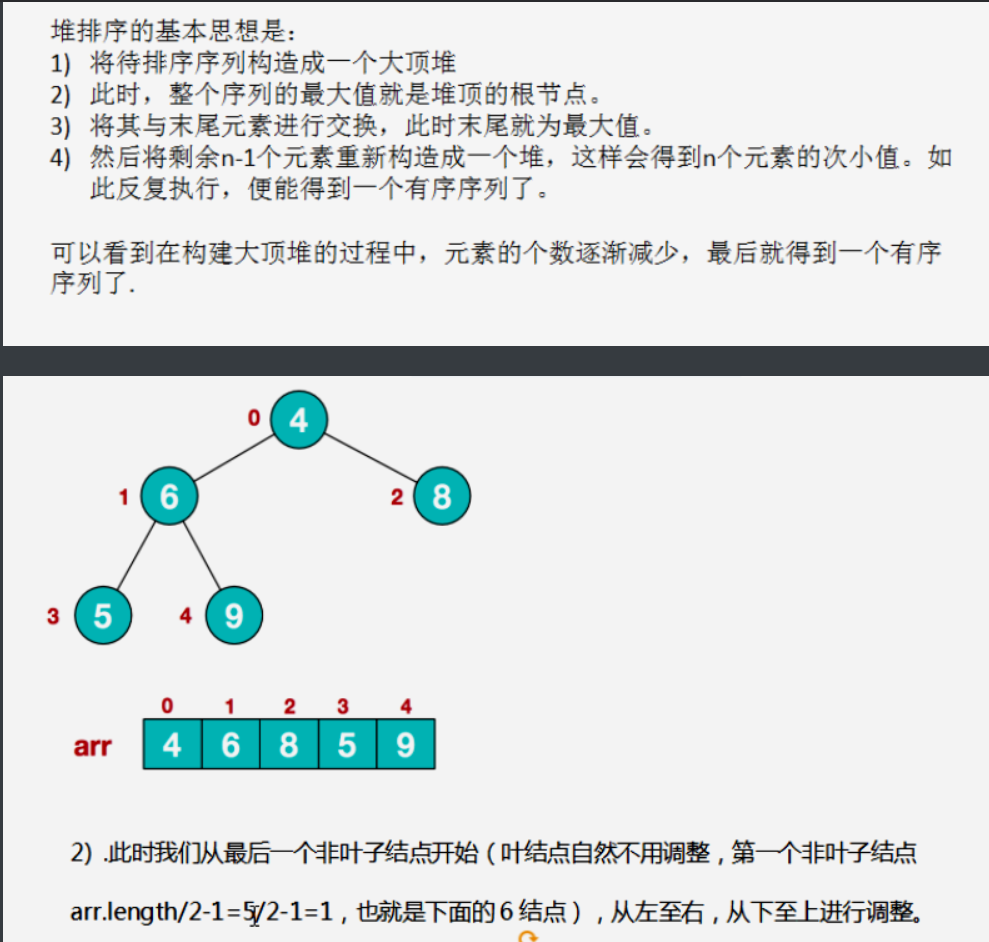

//i: Index of non leaf node in array
//length: decrease gradually, indicating how many elements are adjusted
//Adjust an array (binary tree) to a large top heap
public static void adjustHeap(int arr[], int i, int length){
int temp = arr[i];
//Start adjustment
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
//i * 2 + 1 is the left child node of node i; k = k * 2 + 1 indicates the next left child node of the current node
if (k+1< length && arr[k] < arr[k + 1]) {
k++; //K points to the right child node
}
if (arr[k] > temp) {
arr[i] = arr[k];
i = k;
} else {
break;
}
}
//At the end of the loop, we have placed the maximum value of the tree with i as the parent node at the top (local)
arr[i] = temp;
}
public static void heapSort(int arr[]){
//1. Build an unordered sequence into a heap, and select the large top heap / small top heap according to the ascending and descending requirements
//Arr.length/2 - 1 find the largest non leaf node
for (int i = arr.length / 2 - 1; i >= 0; i--){
adjustHeap(arr, i, arr.length);
} //This is the large top pile
//2. Exchange the top heap element with the end element, and "sink" the largest element to the end of the array
//3. Readjust the structure to meet the heap definition, then continue to exchange the top elements of the heap with the current tail elements, and repeat the adjustment + exchange steps until the whole sequence is in order
for (int j = arr.length - 1; j > 0; j--) {
//exchange
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
}
9, Huffman tree
Basic introduction:
- Given n weights as n leaf nodes, a binary tree is constructed. If the weighted path length of the tree reaches the minimum, it is called the optimal binary tree, also known as Huffman tree.
- Huffman tree is the tree with the shortest weighted path length, the node with larger weight is closer to the root, and the tree with the smallest wpl
- The weight points are located in the leaf node
- Take two smallest root nodes to form a binary tree. The weight of the root node of the binary tree is the sum of the two nodes
matters needing attention:
- The file itself is compressed, and the recompression efficiency will not change significantly by using Huffman coding, such as ppt, video and other files
- Huffman can process all text by binary encoding
- If there is not much duplicate data in a file, the compression effect will not be obvious
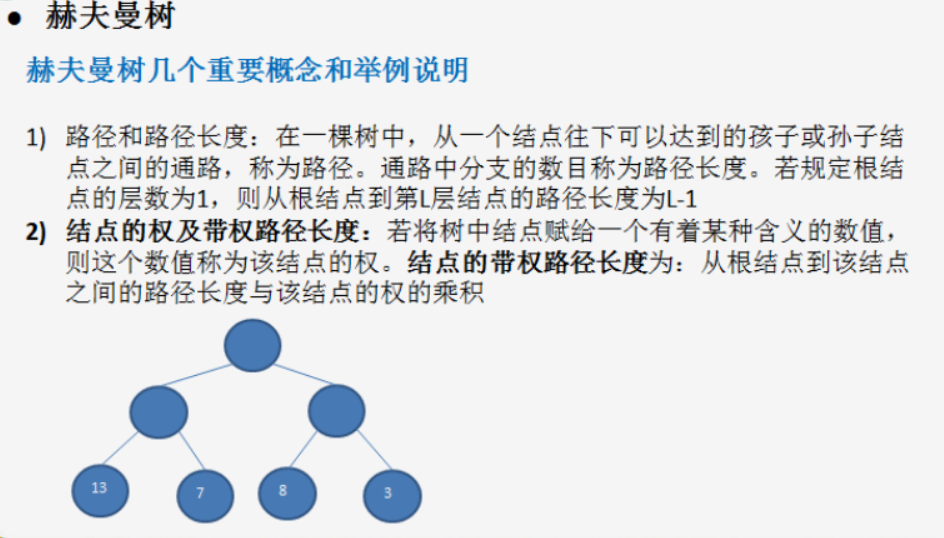
//Create node class
//In order to keep the Node objects sorted, the Collections collection is sorted
class Node implements Comparable<Node>{
int value; //Node weight
Node left;
Node right;
public Node (int value){
this.value = value;
}
//toString
@override
public int compareTo(Node node) {
//Sort from small to large
return this.value - o.value;
}
}
public class HuffmanTree{
//Create Huffman tree
public static NodeX createHuffmanTree(int[] arr) {
//1. Traversal 2 Build each element of arr into Node3 Put Node into ArrayList
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
Collections.sort(nodes);
//Take out the node with the smallest weight (binary tree)
Node left = nodes.get(0);
//Take out the second smallest node
Node right = nodes.get(1);
//
Node parent = new Node(left.value + right.value):
parent.left = left;
parent.right = right;
//Delete the processed binary tree from the list
nodes.remove(left);
nodes.remove(right);
nodes.add(parent);
}
return nodes.get(0);
}
}
9.1 Huffman code
-
A coding algorithm
-
Huffman coding is widely used in data file compression. The compression rate is usually between 20% - 90%, lossless compression
-
Huffman code is a kind of vlc with variable length coding.
-
Fixed length encoding: convert all bytes into binary
-
Variable length coding: first count the occurrence times of characters and code according to the occurrence times of each character. The more the occurrence times, the smaller the coding.
-
Prefix code: the code of characters cannot be the prefix of other character codes. The code that meets this requirement is called prefix code. That is, duplicate codes cannot be matched.
-
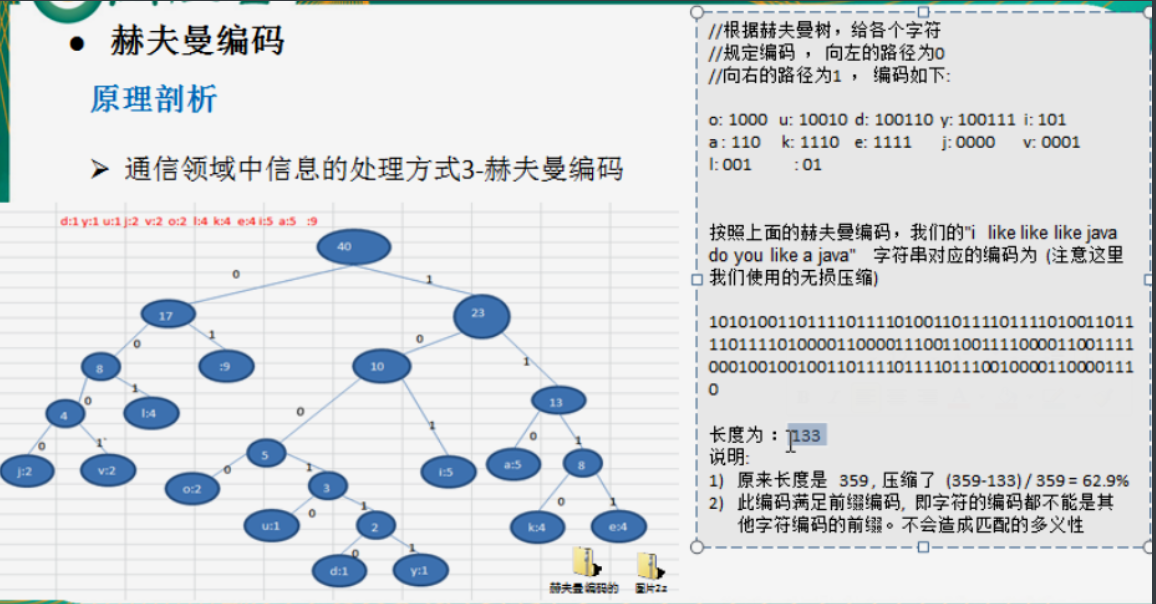
-
instable
9.2 data compression
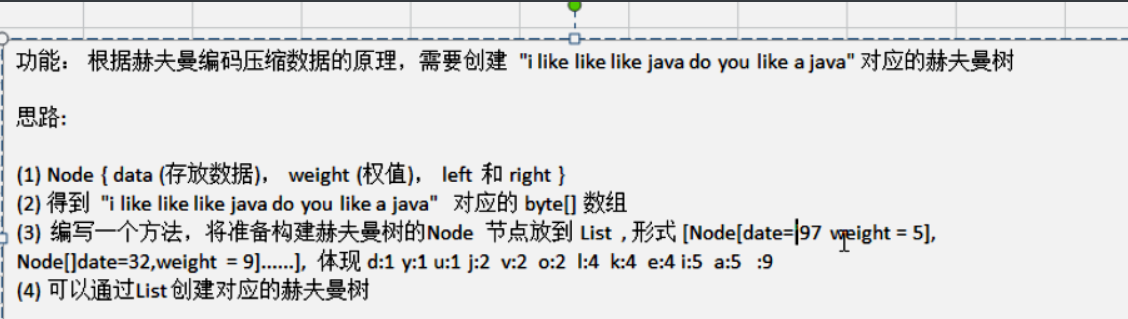
public static void main(String[] args){
String content = "";
byte[] contentBytes = content.getBytes();
}
//Receive byte array and put it back in list
private static List<Node> getNodes(byte[] bytes){
//1. Create an ArrayList
ArrayList<Node> nodes = new ArrayList<Node>();
//Traverse bytes, count the number of occurrences of each byte, and store it in map
Map<Byte, Integer> counts = new HashMap<>();
for (byte b: bytes){
Integer count = counts.get(b);
if (count == null) {
//New characters encountered for the first time
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
//Convert each key value into a Node object and add it to the nodes collection
//Traversal map
for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//
private static Node createHuffmanTree(List<Node> nodes) {
while (nodes.size() > 1) {
//Sort, small to large
Collections.sort(nodes);
//Take out the first smallest binary tree
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//Create a new binary tree. Its root node has no data but only weights
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//Delete the two binary trees that have been processed from nodes
nodes.remove(leftNode);
nodes.remove(rightNode);
//Add a new binary tree to nodes
nodes.add(parent);
}
//The last node of nodes is the root node
return nodes.get(0);
}
//Create Node, data and weight
class Node implements Comparable<Node>{
Byte data; //Store the data (character) itself, such as' a '- 97
int weight; //Weight (number of characters)
Node left;
Node right;
public Node(Byte data, int weight) {
super();
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//Sort from small to large
return this.weight - o.weight;
}
//toString
//Preorder traversal
public void preOrder(){
//syso this
if (this.left != null) this.left.preOrder();
if (this.right != null) this.right.preOrder();
}
}
9.3 generate Huffman code (9.27)
Generating Huffman coding and obtaining Huffman coded data
0 to the left and 1 to the right

//thinking
//1. Store Huffman coding table in map, where map < byte, string >
// Form: 32 > 01, 97 > 100, u > 11001
// 2. While generating Huffman coding table, continuously splice character paths and define a path where StringBuilder stores a leaf node
static StringBuilder stringBuilder = new StringBuilder();
static Map<Byte, String> huffmanCodes = new HashMap<Byte, String>();
main{
List<Node> nodes = getNodes(contentBytes);
Node huffmanTreeRoot = createHuffmanTree(nodes);
getCodes(huffmanTreeRoot, "", sb);// Root node is empty
}
//The Huffman codes of all leaf nodes of the incoming node node are obtained and put into the Huffman codes collection
//code the left child node is 0 and the right child node is 1
private static void getCodes(Node node, String code, StringBuilder sb){
StringBuilder sb2 = new StringBuilder(sb);
sb2.append(code);
if (node != null) {
//Judge whether the current node is a leaf node or a non leaf node
if (node.data == null) {
//Recursive processing of non leaf nodes
getCodes(node.left, "0", sb2);
getCodes(node.right, "1", sb2);
} else {
//Indicates that the last node of a leaf is found
huffmanCodes.put(node.data, sb2.toString());
}
}
}
//The byte [] array corresponding to the string, through the generated Huffman encoding table, returns a byte [] compressed by Huffman encoding
//Get the character array corresponding to Huffman coding table
//Input string and output encoded data
private static byte[] zip(byte[] bytes, Map<Byte, String> hfCode) {
StringBuilder sb = new StringBuilder();
for (byte b : bytes) {
sb.append(hfCode.get(b));
}
// syso sb.toString();
// Add "101010101010....." Convert to byte []
int len; // (sb.length() + 7) / 8;
if (stringBuilder.length() % 8 == 0) {
len = sb.length() / 8;
} else {
len = sb.length() / 8 + 1;
}
//Create byte array to store compressed data
byte[] by = new byte[len];
int index = 0;
for (int i = 0; i < sb.length(); i+= 8) {
//Every 8 bits corresponds to a byte
String strByte;
if (i+8 > sb.length()) {
//The last time is less than 8
strByte = sb.substring(i);
} else {
strByte = sb.substring(i, i + 8);
}
//Convert strbyte into a byte and put it in by
by[inde] = (byte)Integer.parserInt(strByte, 2);
index++;
}
}
9.4 data decompression
1. Convert the original Huffman coded character array into binary string
//1. [-88,-65,-56....] > "10101000..."
//2. "1010100..." > "i like like..."
//Complete the decoding of compressed data
// 1 Huffman encoding table 2 character array obtained by Huffman decoding
private static byte[] decode(Map<Byte, String> hfcodes, byte[] hfbytes) {
//1. Get binary string first
StringBuilder sb = new StringBuilder();
//
for (int i = 0; i < hfcodes.length; i++){
byte b = hfbytes[i];
boolean flag = (i == hfbytes.length - 1);
sb.append(byteToBitString(!flag, b));
}
//2. Decode the string according to the specified Huffman encoding table
// a> 100 > a exchange
Map<String, Byte> map = new HashMap<String, Byte>();
for (Map.Entry<Byte, String> entry : hfcodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
//Create a byte to store for the collection
List<Byte> list = new ArrayList<>();
//
for (int i = 0; i < sb.length; ){
int count = 1; //Counter
boolean flag = true;
Byte b = null;
while (flag) {
//Take out a '1' or '0'
String key = sb.substring(i, i+count);//i don't move, count moves until it matches a character
b = map.get(key);
if (b == null) {
count++;
} else {
//Match to
flag = false;
}
}
list.add(b);
i+=count; //i move directly to count
}
//
byte b = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
//flag: indicates whether to fill the high bit. The last byte does not need to fill the high bit
//return: returns the binary string corresponding to b by complement
private static String byteToBitString(boolean flag, byte b) {
//1. [-88,-65,-56....] > "10101000..."
//Save b with variable
int temp = b;// Convert b to int
//If it is a positive number, there is a high complement
if (flag){
temp |= 256; // Bitwise and 256 1 0000 | 0000 00001 > 1 0000 0001
}
String str = Integer.toBinaryString(temp); //The binary complement corresponding to temp is returned
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
return
}
10, Binary sort tree (BST) (9.28)
Improve retrieval, sorting, addition and deletion
Binary sort tree: (BST: binary sort (search) tree). For any non leaf node of the binary sort tree, the value of the left child node is required to be smaller than that of the current node, and the value of the right child node is required to be larger than that of the current node. The same value is placed on the left or right child node of the point.
10.1 binary sort tree creation and traversal
Create an array into the corresponding binary sort tree, and use the middle order to traverse the binary sort tree (the values traversed by the middle order are orderly)
//Create node
class Node {
int value;
Node left;
Node right;
//constructor
//Add node
public void add(Node node) {
//Adding nodes in the form of recursion needs to meet the requirements of binary sort tree
if (node == null) {
return;
}
//Judge the value of the incoming node and its relationship with the value of the root node of the current subtree
if (node.value < this.value) {
if (this.left == null) {
this.left = node.value;
} else {
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node.value;
} else {
this.right.add(node);
}
}
}
//Middle order traversal
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
//syso this.value
if (this.right != null) {
this.right.infixOrder();
}
}
}
//Create binary sort tree
class BinarySortTree {
private Node root;
//Method of adding nodes
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
//Middle order traversal
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
// null
}
}
//Find the node to delete
public Node search(int value){
if (root == null) return null;
else {
return root.search(value);
}
}
//Find parent node
public Node searchParent(int value){
if (root == null) return null;
else return root.searchParent(value);
}
public int delRightTreeMin(Node node) {
//f returns the value of the smallest node of the binary sort tree with node as the root node
//Delete the smallest node of the binary sort tree whose node is the root node
Node target = node;
while (target.left != null) {
target = target.left;
}
//At this point, the target points to the smallest node
delNode(target.value);//delete
return target.value;
}
//Delete node
public void delNode(int value) {
if (root == null){
return;
} else {
Node targetNode = search(value);
if (targetNode == null) {
return;
}
//If only one node is found
if (root.left == null && root.right == null) {
root == null;
return;
}
//Find the parent node of tgnode
Node parent = searchParent(value);
//If the deleted node is a leaf node
if (targetNode.left == null && targetNode.right == null) {
//Determine whether tg is the left child node or the right child node of the parent node
if (parent.left != null && parent.left.value == value) {
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) {
//Delete a node with two subtrees
int minval = delRightTreeMin(targetNode.right);
targetNode.value = minval;
//Find the smallest from the right subtree
} else {
//Delete the node of a subtree
//Note: when there are two remaining nodes, you need to judge the existence of the root node
if (targetNode.left != null){
if (parent != null) {
if (parent.left.value == value) {
parent.left = targetNode.left;
} else {
parent.right = targetNode.right;
} } else root = targetNode.left;
} else {//The deleted node has a right child node
if (parent != null) {
if (parent.left.value == value) {
parent.left = targetNode.left;
} else {
parent.right = targetNode.right;
} } else root = targetNode.right;
}
}
}
}
}
10.2 deletion of binary sort tree
Consideration:
- Delete the leaf node (1. Find the node to be deleted first. targetNode 2. Find the parent node of targetNode 3. Determine whether the left child node or the right child node. parent.left= null;/ parent.right = null)
- Delete a node with only one subtree(
- 123 \
- target is the left child node of parent: parent left = targetNode. left; \ parent. left = targetNode. right;)
- Delete a node with two subtrees(
- 12 \
- Find the smallest node from the right subtree of targetNode,
- Save the value of the smallest node in temp with a temporary variable,
- Delete the minimum node, t
- argetNode.value = temp;
- //Or find the largest node from the left subtree)
//Find the node to delete
public Node search(int value) {
if (value == this.value) {
return this;
} else if (value < this.value) {
//Left subtree recursive search
if (this.left == null) {
return null;
}
return this.left.search(value);
} else {
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
//Find the parent node of the node you want to delete
public Node searchParent(int value) {
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
if (value < this.value && this.left != null) {
return this.left.searchParent(value);
} else if (value >= this.value && this.right != null) {
//Avoid the same value in actual use
return this.right.searchParent(value);
} else {
//not found
return null;
}
}
}
//Other codes are in the previous section
11, Balanced binary tree (AVL)
Explain the possible problems of binary sort tree, which is also called balanced binary search tree
Case: {1, 2, 3, 4, 5, 6}, the binary tree formed is more like a single linked list, and the query is slower,
Problem analysis: all the left subtrees are empty, the insertion speed is not affected, the query speed is significantly reduced, and the advantages of bst cannot be brought into play. Solution: balance the binary tree.
Basic introduction:
- avl tree to ensure high query efficiency
- Features: the absolute value of the height difference between the left and right subtrees is no more than 1, and both the left and right subtrees are a balanced binary tree.
- Common implementation methods of balanced binary tree: red black tree, avl (algorithm), scapegoat tree, tree and extended tree
11.1 single rotation (left rotation)
Sequence 4 3 2 5 7 8,
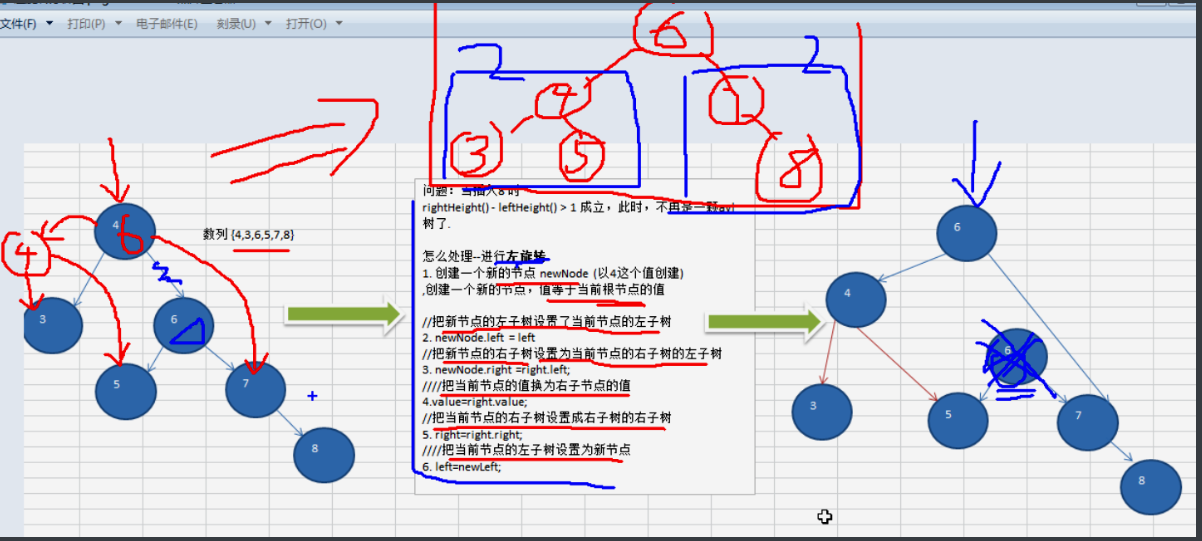
Count the height of the left subtree and the height of the right subtree
class Node {
int value;
Node left;
Node right;
//constructor
//****************************************************************
//Returns the height of the tree with the current node as the root node
public int height(){
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
public int leftHeight(){
if (left == null) return 0;
return left.height();
}
//Returns the height of the right subtree
public int rightHeight(){
if (right == null) return 0;
return right.height();
}
//Left rotation method
private void leftRotate() {
//1. Create a new node to the value of the current root node
Node new = new Node(value);
new.left = left;
new.right = right.left;
value = right.value;
right = right.right;
left = new;
}
//**********************************************************************
//Add node
public void add(Node node) {
//Adding nodes in the form of recursion needs to meet the requirements of binary sort tree
if (node == null) {
return;
}
//Judge the value of the incoming node and its relationship with the value of the root node of the current subtree
if (node.value < this.value) {
if (this.left == null) {
this.left = node.value;
} else {
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node.value;
} else {
this.right.add(node);
}
}
//*************************************
//After adding a node, if (height of right subtree - height of left subtree) > 1, rotate left
if (rightHeight() - leftHeight() > 1) {
// if (right != null && right.rightHeight() < right.leftHeight()) {
//Rotate the right subtree first
//}
//Simple consideration, left rotation
leftRotate();
}
//
if (leftHeight() - rightHeight() > 1) {
rightRotate();
}
}
//Middle order traversal
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
//syso this.value
if (this.right != null) {
this.right.infixOrder();
}
}
}
11.2 right rotation
private void rightRotate(){
Node new = new Node(value);
new.right = right;
new.left = left.right;
value = left.value;
left = left.left;
right = new;
}
11.3 double rotation

Problem analysis:
- When the conditions for right rotation are met
- If the height of the right subtree of its left subtree is greater than the height of its left subtree
- First rotate the left node of the current node
- Then rotate the current node to the right
if(leftHeight() - rightHeight() > 1){
if (left != null && left.rightHeight() > left.leftHeigth()) {
left.leftRotate();
rightRotate();
} else {
rightRotate();
}
return; // Must
}
if (rightHeight() - leftHeight() > 1) {
//If the height of the left subtree of the right subtree is greater than the height of its right subtree
//First rotate the right child node to the right, and then rotate the current node to the left
if (right != null && right.leftHeight() > right.rightHeight()) {
right.rightRotate();
leftRotate();
} else {
leftRotate();
}
return;
}
12, Multiple lookup tree
12.1 binary tree and B-tree
The operation efficiency of binary tree is high, but there are also problems
Node of full binary tree: 2^n-1
The massive number of binary tree nodes causes problems: 1. During construction, i/o operations need to be carried out many times (massive data exists in the database or file). The massive number of nodes has an impact on the speed of constructing binary tree. 2.
2. The nodes are massive and the height of binary tree is very high, which reduces the operation speed.
Multitree:

Number of subtrees of nodes: degree of nodes
Maximum degree of all nodes: the degree of the tree
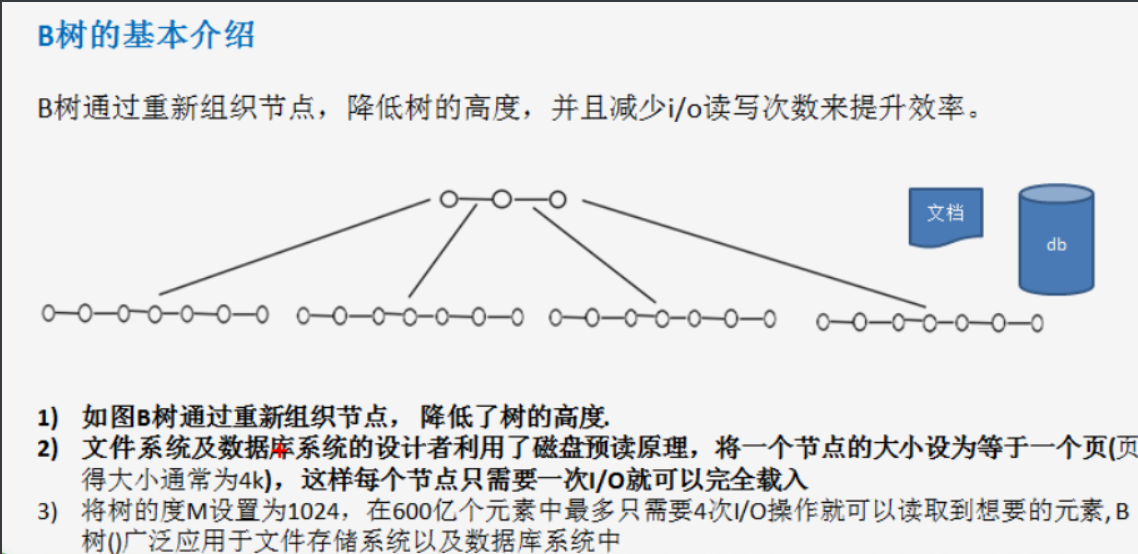
12.2-3 tree (9.29)
2-3 tree is a simple b-tree structure with the following features:
- All leaf nodes of the 2-3 tree are on the same layer (conditions satisfied by the b tree)
- 2-3 tree has only 2 and 3 nodes and 2 nodes (with two nodes or no nodes)
- Meet the characteristics of sorting array and abide by the rules of binary sorting tree
- When a number is inserted to a node according to the regulations, if the above three requirements cannot be met, it needs to be removed. First remove it upward, and if the upper layer is full, remove this layer.

12.3 B tree, B + tree, b * Tree
Balanced
B-tree
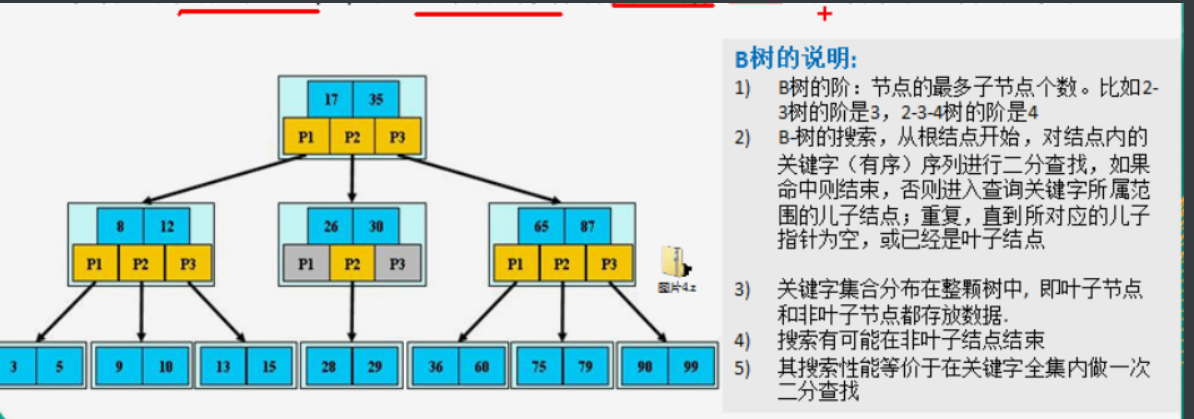
- Order of B tree: 23 tree = 3234 tree = 4, maximum number of child nodes of node
- Search performance: do a binary search in the complete set of keywords
B + tree
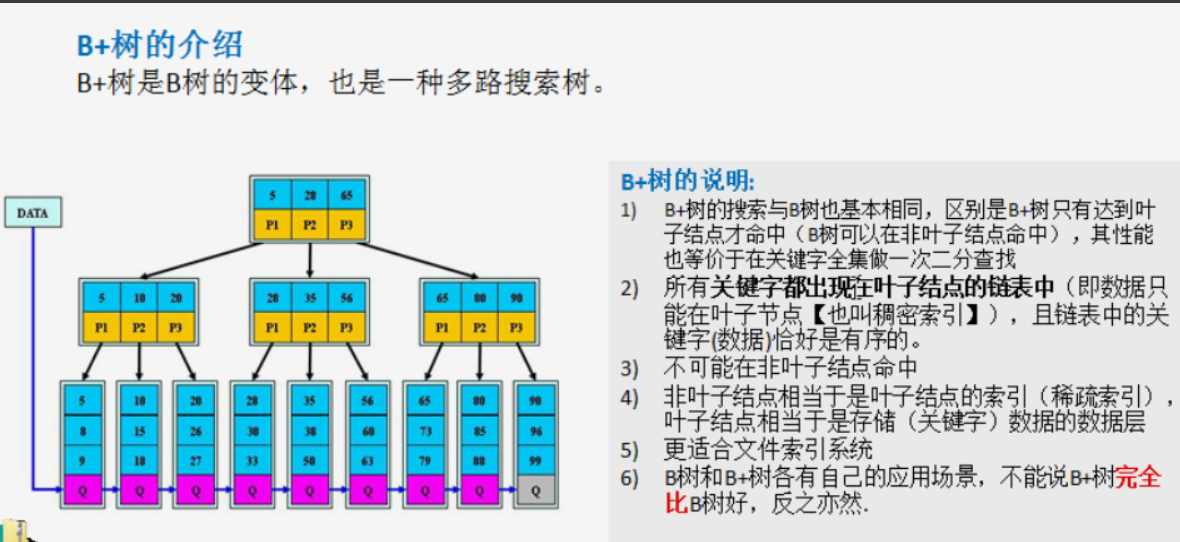
- Keywords are added to the linked list of leaf nodes (dense index)
- A non leaf node is equivalent to the index of a leaf node (sparse index)
B * Tree

13, Figure
Why are there pictures?
- The linear table is limited to the relationship between a direct precursor and a direct successor
- The tree can also have only one direct precursor (parent node)
- When we need to represent many to many relationships, we need to use graphs
Graph is a kind of data structure. Nodes can have zero or more adjacent elements, and there are edges between nodes.
- Undirected graph
- Directed graph
- Weighted graph (net)
Representation:
- Two dimensional array (adjacency matrix)
- Linked list (adjacency list)
13.1 implementation of undirected graph code
//Store vertex String using ArrayList 2 Save matrix int[][] edges
private ArrayList<String> vertexList;
private int[][] edges;//Storage graph corresponding adjacency matrix
private int numOfEdges;
public Graph(int n) {
//Initialize matrix and vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
public void insertVertex(String vertex) {
//Insert node
vertexList.add(vertex);
}
//Add edge
//v12 vertex subscript weight indicates weight
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
//Common methods return the number of nodes
public int getNumOfVertex(){
return vertexList.size();
}
//Get the number of edges
public int getNumOfEdges(){
return numOfEdges;
}
//Returns the data corresponding to the subscript of node i
public String getValue(int i) {
return vertexList.get(i);
}
//Returns the weight of v1 v2
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//Corresponding matrix diagram
13.2 DFS
Basic steps:
- Access node, mark that the node has been accessed
- Find the first adjacent node
- Not accessed, the depth of the modified node takes precedence
//Defines the array boolean [], which records whether a node is accessed
private boolean[] isVisited = new boolean[5];//Initialization is written in the constructor
//Get the subscript of the first adjacent node
public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexList.size(); j++){
if (edges[index][j] > 0) return j;
}
return -1;
}
//Obtain the next adjacent node according to the subscript of the previous adjacent node
public int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vertexList.size(); j++) {
if (edges[v1][j] > 0) return j;
}
return -1;
}
//DFS
public void dfs(boolean[] isVisited, int i) {
//Access node
//syso get(i)+">"
//Tag access
isVisited[i] = true;
//Find the first adjacent node of node i
int w = getFirstNeighbor(i);
while (w != -1) {
if (!isVisited[w]) {
dfs(isVisited, w);
}
//If w has been accessed
w = getNextNeighbor(i, w);
}
}
main{
graph.dfs();
}
//Reload dfs,
public void dfs() {
//Traverse all nodes and perform dfs backtracking
for (int i = 0; i < getNumOfVertex(); i++){
if (!isVisited[i]) {
dfs(isVisited, i);
}
}
}
13.3 BFS
Similar to the hierarchical search process, breadth first search needs to use a queue to maintain the order of visited nodes
//bfs for a node
private void bfs(boolean[] isVisited, int i) {
int u; // Indicates the subscript corresponding to the header node of the queue
int w; //Adjacent node w
//Queue, record order
LinkedList queue = new LinkedList();
//Access node
//syso
//Tag access
isVisited[i] = true;
//Node join queue
queue.addLast(i);
while (!queue.isEmpty()) {
//Take out the subscript of the queue header node
u = (Integer)queue.removeFirst();
//Get the subscript w of the first adjacent node
w = getFirstNeighbor(u);
while (w != -1) {
if(!isVisited[w]) {
//Output access
//Tag access
isVisited[w] = true;
//Join queue
queue.addLast(w);
}
w = getNextNeighbor(u, w);//Continue to find other adjacent node subscripts of the current layer
}
}
}
//Traverse all nodes for breadth first search
public void bfs() {
isVisited = new boolean[verTexList.size()];
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
bfs(isVisited, i);
}
}
}
13.4 summary
14, 10 commonly used algorithms
14.1 non recursive binary search
- The binary search algorithm is only suitable for searching from the ordered sequence (numbers, letters, etc.) and sorting the sequence
- The running time is log time O(logN), and it takes up to logN times to find the target
//Ascending sequence
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) return mid;
else if (arr[mid] > target) {
right = mid - 1;// You need to look to the left
} else {
left = mid + 1;
}
}
return -1;
}
14.2 divide and conquer algorithm
divide and rule
- The complex problem is divided into several identical or similar subproblems, and then the solutions of subproblems that can be solved simply are combined. This technique is the basis of many efficient algorithms, such as sorting (fast sorting, merging) and Fourier transform (fast Fourier transform)
- Solving classical problems: binary search, large integer multiplication, chessboard coverage, merge sort, quick sort, linear time selection, closest point pair problem, round robin schedule, Hanoi tower
14.2.1 divide and conquer Hanoi Tower
- If there is only one disk, a - > C
- N > = 2, as two disks, the bottom disk and the top disk.
- First put the top plate a - > B
- Lowest a - > C
- b all b - > C
//
public static void hT(int num, char a, char b, char c) {
if (num == 1) {
//syso a - > c
} else {
//1. a-b
hT(num - 1, a, c, b);
//2. The bottom plate of a-C
//syso a -> c
//3. From B to c
hT(num - 1, b, a, c);
}
}
14.3 dynamic planning
Application scenario - Knapsack Problem

01 knapsack problem (one for each item at most), complete knapsack problem (without limiting the number of items, it can be changed to 01)
- Solving subproblems
- Different from divide and conquer, the subproblems obtained by decomposition are often not independent of each other. Based on the solution of the next sub stage, it is necessary to establish the solution of the next sub stage
- Dynamic programming can be advanced step by step by filling in the form to obtain the optimal solution
Thought - > formula (Law) - > code
//The i-th item w[i] item weight v[i] item value v[i][j] the maximum value c backpack capacity that can be loaded into the backpack with capacity j in the first I items traversed each time
/*
Fill in the form - find the law - get the formula
1.v[i][0] = v[0][j] = 0 Indicates that the first row and column filled in the table are 0
2.w[i] > j, v[i][j]=v[i-1][j]
//When the capacity of the new product to be added is greater than the capacity of the backpack, the loading strategy of the previous cell is directly used
3.When J > = w [i], v [i] [J] = max {v [I-1] [J], v [I-1] [J-W [i]] + v [i]}
//When the newly added commodity capacity to be added is less than or equal to the capacity of the current backpack, the loading method is as follows:
//v[i-1][j]:Maximum loaded value of the previous cell
//v[i]:Indicates the value of the current item
//v[i-1][j-w[i]]:Maximum value of loading i-1 items into the remaining space j-w[i]
Value of current goods + maximum value of goods in remaining space
*/
public static void main(String[] args) {
int[] w = {1, 4, 3};
int[] val = {1500, 3000, 2000};
int m = 4;
int n = val.length;
//Create a 2D array
int[][] v = new int[n+1][m+1];
for (int i = 0; i < v.length; i++){
v[i][0] = 0;
}
for (int i = 0; i < v[0].length; i++){
v[0][i] = 0;
}
//According to the formula obtained above, dynamic programming is processed
for (int i = 1; i < v.length; i++){
//Do not process the first line
for (int j = 1; j < v[0].length; j++){
//
if (w[i-1] > j){
v[i][j] = v[i-1][j];
} else {
//i starts with 1 and needs - 1
v[i][j] = Math.max(v[i-1][j], val[i - 1]+v[i-1][j-w[i-1]]);
//Record the situation. You can't simply use the formula
if ()
}
}
}
}
14.4 KMP
Application scenario: string matching problem
Determine whether str1 contains str2
14.4.1 violence matching
-
Character matching, for i++, j++
-
Failed, str[i], make i=i-(j-1), j=0
-
A lot of backtracking, moving only one bit at a time, wasting a lot of time, and there are repeated matches
public static int violenceMatch(String str1, String str2) { char[] s1 = str1.toCharArray(); char[] s2 = str2.toCharArray(); int s1len = s1.length; int s2len = s2.length; int i = 0; int j = 0; while (i < s1len && j < s2len) { //Guarantee not to cross the line if (s1[i] == s2[j]) { i++; j++; } else { i = i - (j-1); j = 0; } } if (j == s2len) { return i - j; } else return -1; }
14.4.2 kmp
kmp is a classical algorithm to solve whether the pattern string has appeared in the text string, and if so, the earliest position
Using the previously judged information, save the length of the longest common subsequence in the pattern string through a next array. During each backtracking, find the previously matched position through the next array, saving a lot of calculation time.
How to omit the repeated steps?
Through some search words, the partial matching table of pattern string is calculated.



The essence of partial matching: there will be repetition at the head and tail of the string, and partial matching value is the length of repetition.
main{
str1 = "sdsdsd dsddsd";
str2 = "sd";
}
//kmp search algorithm
public static int kmpSearch(String str1, String str2, int[] next) {
for (int i = 0, j = 0; i < str1.length; i++){
//Need to process STR1 charAt(i) != str2. charAt(j)
// *******kmp core*********
while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
j = next[j - 1];
}
if (str1.charAt(i) == str2.charAt(j)) {
j++;
}
if (j == str2.length()) {//eureka
return i - j + 1;
}
}
return -1;
}
//Gets the partial matching value table of a string (substring)
public static int[] kmpNext(String dest) {
//Create a next array to save some matching values
int[] next = new int[dest.length()];
next[0] = 0;
for (int i = 1, j = 0; i++){
//In case of inequality, we need to obtain a new j from next[j-1] until we find that there is equality and exit
//***********kmp core***********
while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
j = next[j - 1];
}
if (dest.charAt(i) == dest.charAt(j)) {
j++;
}
next[i] = j;
}
return next;
}
14.5 greedy algorithm

Application scenario - set coverage problem
Introduction:
- When solving the problem, the best or optimal choice is taken in each step, so as to hope to lead to the best or optimal algorithm
- The results obtained are not necessarily the optimal results (sometimes the optimal solution), but they are relatively close to the optimal solution
Train of thought analysis:
- Exhaustive method, list all sets. It takes a lot of time.
- Greedy algorithm:

14.6 PLIM algorithm
Road construction problems:
14.6.1 minimum spanning tree (MST)
minimum cost spanning tree
Given a weighted undirected connected graph, if a spanning tree is selected to minimize the sum of weights on all edges of the tree, the characteristics are as follows:
- N vertices, n-1 edges
- Include all vertices
- n-1 edges are all in the graph
- Minimum spanning tree algorithm: prim algorithm, Kruskal algorithm
14.6.2 solution of PLIM algorithm
- Find the so-called minimal connected subgraph
- The algorithm is as follows:
- Let G=(v,e) be a connected graph, T=(u,d) be a minimum spanning tree, vu be a set of vertices, and ed be a set of edges
- If the minimum spanning tree is constructed from the vertex, take the vertex u from the set V and put it into the set, and mark the vertex v with visited[u]=1
- If there are edges between vertex ui in set u and vertex vj in set vu, find the edge with the smallest weight among these edges, but it cannot form a loop. Add vertex vj to set u, and add edges ui and vj to set d, indicating vj=1
- Repeat 2 until UVs are equal and mark visited
//prim
main{
}
//Create minimum spanning tree, figure
class MinTree{
//Create adjacency matrix of graph
public void createMragph(MGraph graph, int verxs, char data[], int[][] weight) {
int i, j;
for (i = 0; i < verxs; i++){
graph.data[i] = data[i];
for (j = 0; j < verxs; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
//Show adjacency matrix of graph
//Write prim algorithm to get the minimum spanning tree
public void prim(MGraph graph, int v) {
//v represents the vertex of the graph
int visited[] = new int[graph.verxs]; // Mark whether the vertex has been accessed
//Mark the current node as accessed
visited[v] = 1;
//h1 h2 records the subscripts of two vertices
int h1 = -1;
int h2 = -1;
int minWeight = 10000;//Initialize a larger value and it will be replaced
for (int k = 1; k < graph.verxs; k++) {
for (int i = 0; i < graph.verxs; i++) {//Traverse visited nodes
for (int j = 0; j < graph.verxs; j++) {//Traverse nodes that have not been accessed
if (visited[i] == 1 && visited[j] ==0 && graph.weight[i][j] < minWeight) {
//Replace minWeight
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}}
//Find an edge
visited[h2] = 1;
minWeight = 10000;
}
}
}
class MGraph{
int verx; //Represents the number of nodes in the graph
char[] data;//Store node data
int[][] weight;//Storage edge, adjacency matrix
public MGragh(int verxs){
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}
14.7 kruskar
Bus station connectivity
Firstly, a forest with only n vertices is constructed, and then edges are selected from the connected network to join the forest according to the weight from small to large, so that there is no loop in the forest until the forest becomes a tree.
A weight sorting b adds the edge with the smallest weight in turn, and does not generate a loop. By judging whether there are the same final vertices
a - sorting algorithm
b - record the end point of the vertex in the "minimum spanning tree". The end point of the vertex is "the largest vertex connected with it in the minimum spanning tree". Then each time you need to add an edge to the minimum spanning tree, judge whether the end points of the two vertices of the edge coincide. If they coincide, a loop will be formed. The two vertices of the added edge cannot all point to the same end point.
//Get the end point () of the vertex with subscript i, which is used to judge whether the end points of the two vertices are the same
//The ends array records the corresponding end point of each vertex. The ends array is formed step by step in the process of traversal
private int getEnd(int[] ends, int i) {
while (ends[i] != 0) {
i = ends[i];
}
return i;
}
//Sort vertex classes
//kruskal
public void kruskal() {
int index = 0; //Represents the index of the last result array
int[] ends = new int[edgeNum]; //Used to save the end point of each vertex in the existing minimum spanning tree in the tree
//Create a result array and save the last minimum spanning tree
EData[] rets = new EData[edgeNum];
//Get the set of all edges in the graph,
EData[] edges = getEdges();
//Sort according to the weight of edges (from small to large)
sortEdges(edges);
//Traverse the edges array. When adding edges to the spanning tree, judge whether the added edges form a loop. If not, add rets, otherwise you can't join
for (int i = 0; i < edgeNum; i++) {
//Gets the first vertex (starting point) to the ith edge
int p1 = getPosition(edges[i].start);
//
int p2 = getPosition(edges[i].end);
int m = getEnd(ends, p1);
//Get p2 the vertex at the end of the existing minimum spanning tree
int n = getEnd(ends, p2);
//Does it constitute a loop
if (m != n) {
ends[m] = n;//Set the end point of m in ends < e, f >
rets[index++] = edges[i]; //Add an edge
}
}
}
14.8 dijestra
Shortest path problem
The main feature is to take the starting point as the center and expand to the outer layer (breadth first search idea) until it is extended to the end.
[the external link image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-umlx6h52-16447321619) (\ data structure and algorithm \ image.png)]
i] = data[i];
for (j = 0; j < verxs; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
//Show adjacency matrix of graph
//Write prim algorithm to get the minimum spanning tree
public void prim(MGraph graph, int v) {
//v represents the vertex of the graph
int visited[] = new int[graph.verxs]; // Mark whether the vertex has been accessed
//Mark the current node as accessed
visited[v] = 1;
//h1 h2 records the subscripts of two vertices
int h1 = -1;
int h2 = -1;
int minWeight = 10000;//Initialize a larger value and it will be replaced
for (int k = 1; k < graph.verxs; k++) {
for (int i = 0; i < graph.verxs; i++) {//Traverse visited nodes
for (int j = 0; j < graph.verxs; j++) {//Traverse nodes that have not been accessed
if (visited[i] == 1 && visited[j] ==0 && graph.weight[i][j] < minWeight) {
//Replace minWeight
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}}
//Find an edge
visited[h2] = 1;
minWeight = 10000;
}
}
}
class MGraph{
int verx; // Represents the number of nodes in the graph
char[] data;// Store node data
int[][] weight;// Storage edge, adjacency matrix
public MGragh(int verxs){
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}
#### 14.7 kruskar
Bus station connectivity
First, construct a n Then select edges from the connected network to join the forest according to the weight from small to large, and make no loop in the forest until the forest becomes a tree.
a Weight sorting b The edge with the smallest weight is added in turn, and no loop is generated, By judging whether there are the same final vertices
a - Sorting algorithm
b - Record the end point of the vertex in the "minimum spanning tree". The end point of the vertex is "the largest vertex connected with it in the minimum spanning tree". Then each time you need to add an edge to the minimum spanning tree, judge whether the end points of the two vertices of the edge coincide. If they coincide, a loop will be formed. The two vertices of the added edge cannot all point to the same end point.
```java
//Get the end point () of the vertex with subscript i, which is used to judge whether the end points of the two vertices are the same
//The ends array records the corresponding end point of each vertex. The ends array is formed step by step in the process of traversal
private int getEnd(int[] ends, int i) {
while (ends[i] != 0) {
i = ends[i];
}
return i;
}
//Sort vertex classes
//kruskal
public void kruskal() {
int index = 0; //Represents the index of the last result array
int[] ends = new int[edgeNum]; //Used to save the end point of each vertex in the existing minimum spanning tree in the tree
//Create a result array and save the last minimum spanning tree
EData[] rets = new EData[edgeNum];
//Get the set of all edges in the graph,
EData[] edges = getEdges();
//Sort according to the weight of edges (from small to large)
sortEdges(edges);
//Traverse the edges array. When adding edges to the spanning tree, judge whether the added edges form a loop. If not, add rets, otherwise you can't join
for (int i = 0; i < edgeNum; i++) {
//Gets the first vertex (starting point) to the ith edge
int p1 = getPosition(edges[i].start);
//
int p2 = getPosition(edges[i].end);
int m = getEnd(ends, p1);
//Get p2 the vertex at the end of the existing minimum spanning tree
int n = getEnd(ends, p2);
//Does it constitute a loop
if (m != n) {
ends[m] = n;//Set the end point of m in ends < e, f >
rets[index++] = edges[i]; //Add an edge
}
}
}
14.8 dijestra
Shortest path problem
The main feature is to take the starting point as the center and expand to the outer layer (breadth first search idea) until it is extended to the end.
