Niuke video summary 2

Double pointer problem

Task 1: sort left and right

Given an array arr and a number num, please put the number less than or equal to num on the left of the array and the number greater than num on the right of the array.
Additional space complexity required O ( 1 ) O(1) O(1), time complexity is O ( N ) O(N) O(N)

Answer: the same as below, but only the area less than or equal to exists. If it is less than or equal to, the next number of the area less than or equal to will be exchanged

Task 2: the Dutch flag

Given an array arr and a number num, please put the number less than num on the left of the array, the number equal to num in the middle of the array, and the number greater than num on the right of the array.
Additional space complexity required O ( 1 ) O(1) O(1), time complexity is O ( N ) O(N) O(N)

Answer:
Three things like pointers, one for less, one for more and one for cur
Assume num=5
If the number of current positions = 5, the cur pointer moves backward;
If the number of current positions is less than 5, less than the area expansion, less + +, cur + +;
If the number of current positions > 5, it is larger than the area expansion, and more –, cur remains unchanged (because it is uncertain what number is exchanged)
Termination condition: cur==more

public static int[] partition(int[] arr, int L, int R, int num){
	less = L-1;
	more = R+1;
	cur = L;
	while(cur < more){
		if(arr[cur]=num){
			cur++;
		}
		else if(arr[cur]<num){
			swap(arr, ++less, cur++);
		}
		else{
			swap(arr, --more, cur);
		}
	}
	return new int[]{less+1,more-1};
}

public static void swap(int[] arr, int a, int b){
	int tem = arr[a];
	arr[a] = arr[b];
	arr[b] = tem;
}

Quick sort

Ordinary fast platoon (similar to Dutch flag)

Take the fixed position, generally take the first or last one as the benchmark, and then put the one smaller than the benchmark on the left and the one larger than the benchmark on the right. It is to exchange with the benchmark. After the exchange, the left is smaller than the benchmark and the right is larger than the benchmark. In this way, an array is divided into two sub arrays, and then the sub array is divided into smaller sub arrays in the same way until it cannot be decomposed.

Problem: the worst case is that the last number selected is the largest or smallest, because this is equivalent to only arranging the last one at a time, and the time complexity is O ( N 2 ) O(N^2) O(N2)； The best situation is that the last number selected is just in the middle and can continue to be arranged in two, so the time complexity is O ( N l o g N ) O(NlogN) O(NlogN). It can be concluded that the complexity of classical fast scheduling is related to data.

Random fast platoon (improved fast platoon)

Random fast sorting bypasses the original data and solves the problems of the original data from the perspective of probability. In other words, in the random fast scheduling, the last number is not found as the benchmark, but an arbitrary number is selected from the array with equal probability to exchange with the current last number, so that the selected number is used as the benchmark. Therefore, using probability accumulation to calculate the complexity, the long-term expected complexity is O ( N l o g N ) O(NlogN) O(NlogN)

The additional space complexity of random fast scheduling is O ( l o g N ) O(logN) O(logN), because it is necessary to record the saved breakpoints, and the number of breakpoints is the depth of recursion. The extra space complexity of random fast sorting is lower than that of merging sorting!

Simple understanding of heap

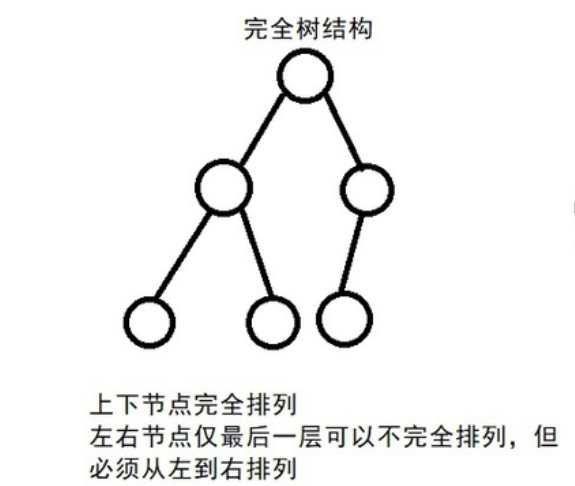
Complete binary tree

1. Full binary tree (all non leaf nodes have 2 children);
2. Not full binary tree, but complete the nodes from left to right
   

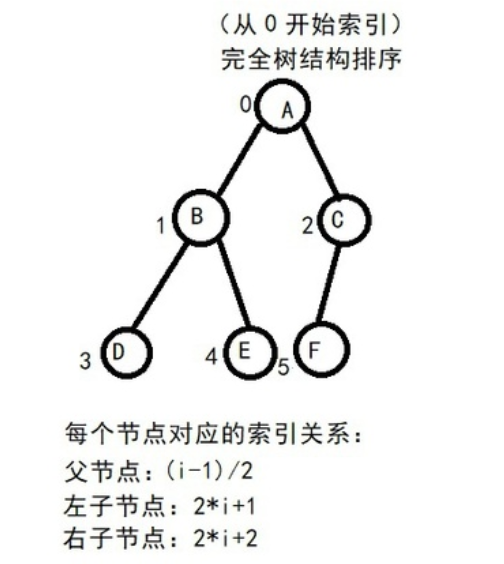
Parent child node index

The left child node index of 1 node i is 2 ∗ i + 1 2*i+1 2∗i+1； The right child node index is 2 ∗ i + 2 2*i+2 2∗i+2； Parent node is ( i − 1 ) / 2 (i-1)/2 (i−1)/2.

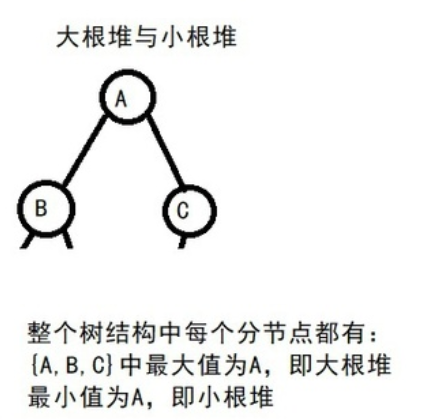
Large root pile and small root pile

A heap is a complete binary tree. In this complete binary tree, the maximum value of any sub tree is the head, and the complete binary tree is the large root heap; On the contrary, a complete binary tree whose minimum value is the head is the small root heap.

heapInsert (the entire heap becomes larger)

2，1，3，6，0，4

• First look at [2,1], arrange the large root pile as [2,1]
• Add in 3, compare 3 with parent node 2 and exchange [3,1,2], and then compare 3 with child node without exchange to obtain [3,1,2]
• Add 6 and compare it with parent node 2 and exchange it as [3,6,2,1], then compare it with parent node 3 and exchange [6,3,2,1], and then compare 6 with child node without exchange to obtain [6,3,2,1]
• Add 0 and compare it with parent node 3. Do not exchange and get [6,3,2,1,0]
• Add 4 and compare it with parent node 2 to exchange [6,3,4,1,0,2]. Then compare 4 with parent node 6 and do not exchange, and get [6,3,4,1,0,2]

Every step can look up O ( l o g N ) O(logN) O(logN), the total time complexity is l o g 1 + l o g 2 + . . . + l o g N − 1 log1+log2+...+logN-1 log1+log2+...+logN − 1. After calculation, the overall time complexity is O ( N ) O(N) O(N)

public static void heapInsert(int[] arr, int index){
        while(arr[index]>arr[(index-1)/2]){
            swap(arr, index, (index-1)/2);
            index = (index-1)/2;
        }
}

Some data in large root heap becomes smaller (heapify)

6, 5, 4, 2, 5, 2. If you change 6 to 0, how does the large root heap change
A: look down for the left and right children and exchange with the older one

• [0,5,4,2,5,2], 0 is compared with the left child node 5 and the right child node 4, and exchanged with 5 [5,0,4,2,5,2]
• 0 is compared with the left child node 2 and the right child node 5, and it is exchanged with 5 to get [5,5,4,2,0,2]

public static void heapify(int[] arr, int index, int heapSize){
        int left = 2*index+1;
        int right = 2*index+2;
        while(left<heapSize){
            int max = right < heapSize && arr[left] < arr[right] ? right : left;
            int largest = arr[index] > arr[max] ? index : max;//Pay attention to the direction. If there is no right child node, you have to use the left child node
            if(largest==index){
                break;
            }
            swap(arr, index, largest);
            index = largest;
            left = index*2+1;
            right = index*2+2;
        }
    }

Quickly find the median from the data stream

• Create a large root pile and a small root pile (expect the number in each pile to be N / 2 N/2 N/2), the first number enlarges the root heap
• If the number of large root piles exceeds, discard the root of the large root pile and put it into the small root pile, and then heapify; If the number of small root piles exceeds, discard the root of the small root pile, put it into the large root pile, and then heapify.

Heap sort

• Array becomes large root heap (large root heap may not be ordered)
• The root data is exchanged with the last data so that a maximum value can be found
• Except for the last position, heapify other parts
• Repeat step 2.3 until the heap size is 0

Time complexity O ( N l o g N ) O(NlogN) O(NlogN)

public class Heapsort {
    public static void main(String[] args) {
        int[] arr = new int[]{4,2,4,6,7,8,3,0};
        heapSort(arr);
        for(int i=0;i<arr.length;i++){
            System.out.println(arr[i]);
        }
    }

    public static void heapInsert(int[] arr, int index){
        while(arr[index]>arr[(index-1)/2]){
            swap(arr, index, (index-1)/2);
            index = (index-1)/2;
        }
    }
    public static void heapify(int[] arr, int index, int heapSize){
        int left = 2*index+1;
        int right = 2*index+2;
        while(left<heapSize){
            int max = right < heapSize && arr[left] < arr[right] ? right : left;
            int largest = arr[index] > arr[max] ? index : max;
            if(largest==index){
                break;
            }
            swap(arr, index, largest);
            index = largest;
            left = index*2+1;
            right = index*2+2;
        }
    }

    public static void heapSort(int[] arr){
        if(arr==null || arr.length==1){
            return;
        }
        for(int i=1;i<arr.length;i++){
            heapInsert(arr, i);
        }
        int heapSize = arr.length;
        swap(arr, 0, --heapSize);
        while(heapSize>0){
            heapify(arr, 0, heapSize);
            swap(arr, 0, --heapSize);
        }
    }

    public static void swap(int[] arr, int a, int b){
        int tem = arr[a];
        arr[a] = arr[b];
        arr[b] = tem;
    }
}