540. A single element in an ordered array

2022.2.14 one question per day

Title Description

Give you an ordered array of integers, where each element will appear twice and only one number will appear once.

Please find and return the number that appears only once.

The solution you design must meet O(log n) time complexity and O(1) space complexity.

Example 1:

Input: num = [1,1,2,3,3,4,4,8,8]
Output: 2

Example 2:

Input: num = [3,3,7,7,10,11,11]
Output: 10

Tips:

1 <= nums.length <= 10^5
0 <= nums[i] <= 10^5

Source: LeetCode
Link: https://leetcode-cn.com/problems/single-element-in-a-sorted-array
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

A dichotomy,

class Solution {
    public int singleNonDuplicate(int[] nums) {
        //XOR is On
        //If logarithmic complexity is binary, why binary
        //There are odd numbers. If the current number is the even number and the previous number is the same as the current number, it means that the previous numbers are paired
        //If the previous number is different from the current number, it means that the previous number has a separate value
        //If the current number is an odd number, then look at the previous one. If it is the same as the previous one, then the previous one is also wrong

        int n = nums.length;
        int left = 0;
        int right = n - 1;
        while(left < right){
            int mid = (right - left) / 2 + left;
            //If the current number is even
            if((mid + 1) % 2 == 0){
                //If it is the same as the previous one, it means that there is no separate number in front
                if(mid > 0 && (nums[mid] == nums[mid - 1])){
                    left = mid + 1;
                }else{
                    right = mid - 1;
                }
            }else{
                if(mid > 0 && (nums[mid] == nums[mid - 1])){
                    right = mid - 2;
                }else{
                    left = mid;
                }
            }
        }
        return nums[left];
    }
}

So what is the main learning of this problem? It is the XOR of official solution
If it is an odd number, then XOR is looking for the previous number; If it is an even number, XOR is looking for the latter number
So you can combine two logic into one logic

If the current subscript is an even number, then the ratio with the latter number is the same, indicating that there is no problem in the front
If the current subscript is an odd number, then the ratio with the previous number, if the same, is no problem
Can write together

class Solution {
    public int singleNonDuplicate(int[] nums) {
        int n = nums.length;
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] == nums[mid ^ 1]) l = mid + 1;
            else r = mid;
        }
        return nums[r];
    }
}


Author: AC_OIer
 Link: https://leetcode-cn.com/problems/single-element-in-a-sorted-array/solution/gong-shui-san-xie-er-duan-xing-fen-xi-yu-17nv/
Source: force buckle( LeetCode)
The copyright belongs to the author. For commercial reprint, please contact the author for authorization. For non-commercial reprint, please indicate the source.

1380. Lucky numbers in the matrix

2022.2.15 one question per day

Title Description

Give you a matrix of m * n, the numbers in the matrix are different. Please return all lucky numbers in the matrix in any order.

Lucky number refers to the elements in the matrix that meet the following two conditions at the same time:

The smallest of all elements in the same row
Maximum of all elements in the same column

Example 1:

Input: matrix = [[3,7,8],[9,11,13],[15,16,17]]
Output: [15]
Explanation: 15 is the only lucky number because it is the minimum value in its row and the maximum value in its column.

Example 2:

Input: matrix = [[1,10,4,2],[9,3,8,7],[15,16,17,12]]
Output: [12]
Explanation: 12 is the only lucky number because it is the minimum value in its row and the maximum value in its column.

Example 3:

Input: matrix = [[7,8],[1,2]]
Output: [7]

Tips:

m == mat.length
n == mat[i].length
1 <= n, m <= 50
1 <= matrix[i][j] <= 10^5
All elements in the matrix are different

Source: LeetCode
Link: https://leetcode-cn.com/problems/lucky-numbers-in-a-matrix
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

simulation

class Solution {
    public List<Integer> luckyNumbers (int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;

        int[] hang = new int[m];

        int[] lie = new int[n];
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(matrix[i][j] < matrix[i][hang[i]]){
                    hang[i] = j;
                }
                if(matrix[i][j] > matrix[lie[j]][j])
                    lie[j] = i;
            }
        }

        List<Integer> res = new ArrayList<>();
        for(int i = 0; i < m; i++){
            if(lie[hang[i]] == i)
                res.add(matrix[i][hang[i]]);
        }
        return res;
    }
}

1719. Number of schemes for reconstructing a tree

2022.2.16 one question per day

Title Description

Give you an array pairs, where pairs[i] = [xi, yi], and satisfy:

pairs There are no duplicate elements in
xi < yi

Let ways be the number of rooted tree schemes that meet the following conditions:

All node values contained in the tree are pairs Yes.
A number pair [xi, yi] Appear in pairs If and only if xi yes yi Ancestors or yi yes xi Our ancestors.
Note: the constructed tree is not necessarily a binary tree.

Two trees are treated as different schemes when there is at least one node and there are different parent nodes in the two trees.

Please return to:

If ways == 0 ，Return 0.
If ways == 1 ，Return to 1.
If ways > 1 ，Return to 2.

A rooted tree refers to a tree with only one root node, and all edges are from the root to the outside.

We say that any node on the path from the root to a node (excluding the node itself) is the ancestor of the node. The root node has no ancestors.

Example 1:

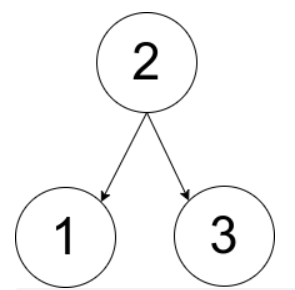
Input: pairs = [[1,2],[2,3]]
Output: 1
Explanation: as shown in the figure above, there is and only one qualified rooted tree.

Example 2:

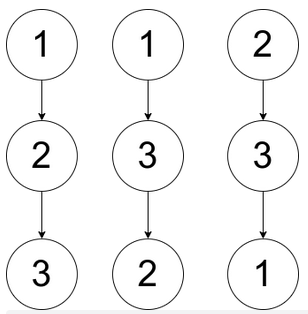
Input: pairs = [[1,2],[2,3],[1,3]]
Output: 2
Explanation: there are several qualified rooted trees, three of which are shown in the figure above.

Example 3:

Input: pairs = [[1,2],[2,3],[2,4],[1,5]]
Output: 0
Explanation: there is no root tree that meets the requirements.

Tips:

1 <= pairs.length <= 10^5
1 <= xi < yi <= 500
The elements in pairs are different from each other.

Source: LeetCode
Link: https://leetcode-cn.com/problems/number-of-ways-to-reconstruct-a-tree
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

To tell you the truth, it's really hard
After reading the explanation, it was written in great detail. You can still understand it carefully, but you don't want to study it carefully at home, cv

class Solution {
    public int checkWays(int[][] pairs) {
        //According to the third example, we can understand the meaning of a question, that is, all relationships will be given in the pairs array
        //In the third example, because the relationships in the constructed tree are not given in pairs, a tree cannot be formed
        //In other words, relationships in pairs cannot form a tree

        Map<Integer, Set<Integer>> adj = new HashMap<Integer, Set<Integer>>();
        for (int[] p : pairs) {
            adj.putIfAbsent(p[0], new HashSet<Integer>());
            adj.putIfAbsent(p[1], new HashSet<Integer>());
            adj.get(p[0]).add(p[1]);
            adj.get(p[1]).add(p[0]);
        }
        /* Detect whether there is a root node*/
        int root = -1;
        Set<Map.Entry<Integer, Set<Integer>>> entries = adj.entrySet();
        for (Map.Entry<Integer, Set<Integer>> entry : entries) {
            int node = entry.getKey();
            Set<Integer> neighbours = entry.getValue();
            if (neighbours.size() == adj.size() - 1) {
                root = node;
            }
        }
        if (root == -1) {
            return 0;
        }

        int res = 1;
        for (Map.Entry<Integer, Set<Integer>> entry : entries) {
            int node = entry.getKey();
            Set<Integer> neighbours = entry.getValue();
            if (node == root) {
                continue;
            }
            int currDegree = neighbours.size();
            int parent = -1;
            int parentDegree = Integer.MAX_VALUE;

            /* Find the parent node of node according to the size of degree */
            for (int neighbour : neighbours) {
                if (adj.get(neighbour).size() < parentDegree && adj.get(neighbour).size() >= currDegree) {
                    parent = neighbour;
                    parentDegree = adj.get(neighbour).size();
                }
            }
            if (parent == -1) {
                return 0;
            }

            /* Detect whether neighbors are a subset of adj[parent] */
            for (int neighbour : neighbours) {
                if (neighbour == parent) {
                    continue;
                }
                if (!adj.get(parent).contains(neighbour)) {
                    return 0;
                }
            }
            if (parentDegree == currDegree) {
                res = 2;
            }
        }
        return res;

    }
}