1, Title Requirements

• Give you the root node of a binary tree, root, and judge whether it is an effective binary search tree.
• A valid binary search tree is defined as follows:
• • The left subtree of a node contains only the number less than the current node.
• • The right subtree of a node only contains a number greater than the current node.
• • All left and right subtrees themselves must also be binary search trees.
• Example 1:

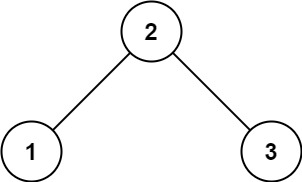
Input: root = [2,1,3]
Output: true

• Example 2:

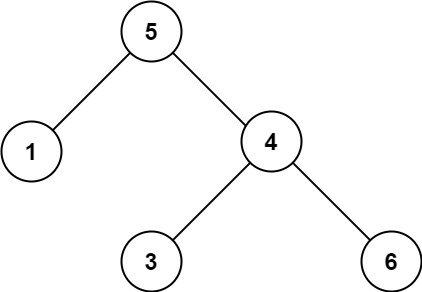
Input: root = [5,1,4,null,null,3,6]
Output: false
 Explanation: the value of the root node is 5, but the value of the right child node is 4.

• Tips:
• • The number of nodes in the tree is within [1, 104];
• • -231 <= Node.val <= 231 - 1.

2, Solving algorithm

① Middle order traversal

• During the middle order traversal, judge whether the current node is greater than the previous node of the middle order traversal. If greater than, it indicates that the BST is met and continue the traversal; Otherwise, false is returned directly.
• Java example:

class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        // Access left subtree
        if (!isValidBST(root.left)) {
            return false;
        }
        // Accessing the current node: if the current node is less than or equal to the previous node traversed in the middle order, it indicates that it does not meet the BST and returns false; Otherwise, continue to traverse.
        if (root.val <= pre) {
            return false;
        }
        pre = root.val;
        // Access right subtree
        return isValidBST(root.right);
    }
}

② Recursion

• The nature of binary search tree is that the values of all nodes in the left subtree are less than (here is < rather than < =) the root node, and the values of all nodes in the right subtree are greater than (similarly, here is > rather than > =) the root node;
• Direct recursion: when verifying the left subtree, the minimum range and maximum range of the left subtree value are passed in as parameters, and the same is true for the right subtree;
• You may have a question: isn't BST small on the left and big on the right? Just check the root val > root. left. Val and root val < root. right. Why not? This is not right, because the feature of BST with small left and large right refers to root Val is larger than all nodes in the left subtree and smaller than all nodes in the right subtree. Of course, it is not enough to check only the left and right subtrees.
• Java example:

// The subtree node with root as the root must meet max.val > root val > min.val
var isValidBST = function (root, min = -Infinity, max = Infinity) {
  // If the node is empty
  if (!root) return true;
  // If root Val does not meet the limits of max and min, indicating that it is not a legal BST (so the judgment condition is < = instead of <, and also > = instead of >)
  if (root.val <= min || root.val >= max) return false;
  // Limit the maximum value of the left subtree to root Val, the minimum value of the right subtree is root val
  return (
    isValidBST(root.left, min, root.val) &&
    isValidBST(root.right, root.val, max)
  );
};

• You can continue to simplify:

// The subtree node with root as the root must meet max.val > root val > min.val
var isValidBST = function (root, min = -Infinity, max = Infinity) {
  // If it is an empty node
  if (!root) return true;
  // The value of the current node is greater than the minimum value and less than the maximum value; (in other words, the value of the current node is greater than that of all nodes in the left subtree and less than that of all nodes in the right subtree)
  // Limit the maximum value of the left subtree to root Val, the minimum value of the right subtree is root val
  return (
    root.val > min &&
    root.val < max &&
    isValidBST(root.left, min, root.val) &&
    isValidBST(root.right, root.val, max)
  );
};

③ LeetCode official solution

• Recursion:
• • To solve this problem, we must first understand what properties of the binary search tree can be used. From the information given by the topic, we can know: if the left subtree of the binary tree is not empty, the values of all nodes on the left subtree are less than the values of its root node; If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of its root node; Its left and right subtrees are also binary search trees.
• • This inspires us to design a recursive function helper(root, lower, upper) to recursively judge. The function means to consider the subtree with root as the root and judge whether the values of all nodes in the subtree are within the range of (l,r) (note that it is an open interval). If the value val of the root node is not within the range of (l,r), it indicates that it does not meet the conditions and returns directly. Otherwise, it is necessary to continue the recursive call to check whether its left and right subtrees meet the requirements. If they all meet the requirements, it indicates that this is a binary search tree.
• • Then, according to the nature of binary search tree, when recursively calling the left subtree, you need to change the upper bound to root Val, that is, call helper(root.left, lower, root.val), because the values of all nodes in the left subtree are less than those of its root node. Similarly, when calling the right subtree recursively, you need to change the lower bound to root Val, that is, call helper(root.right, root.val, upper).
• • The entry of recursive function call is helper(root, -inf, +inf), and inf represents an infinite value.
• • Take example 2:

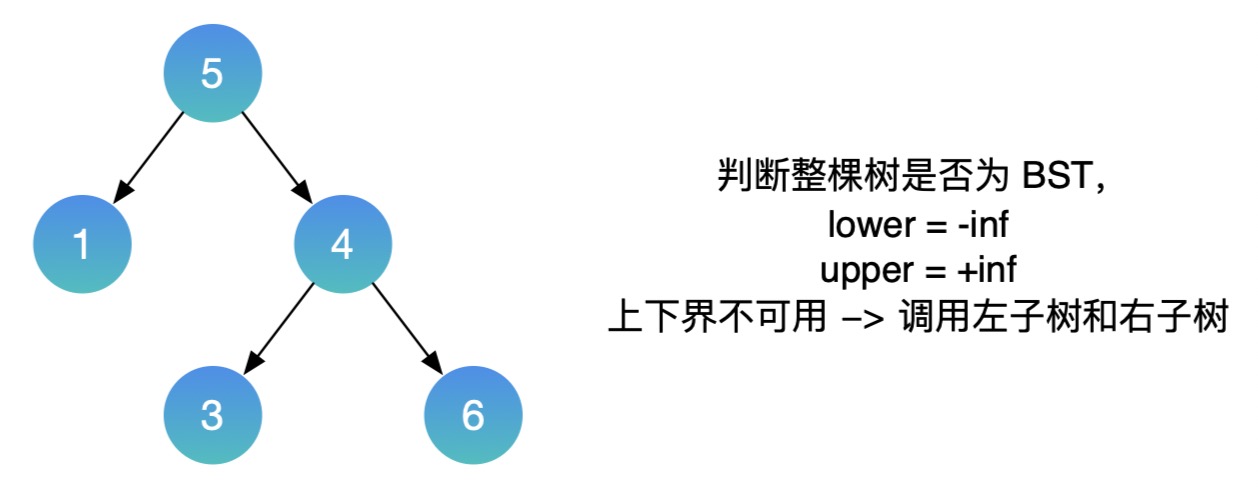
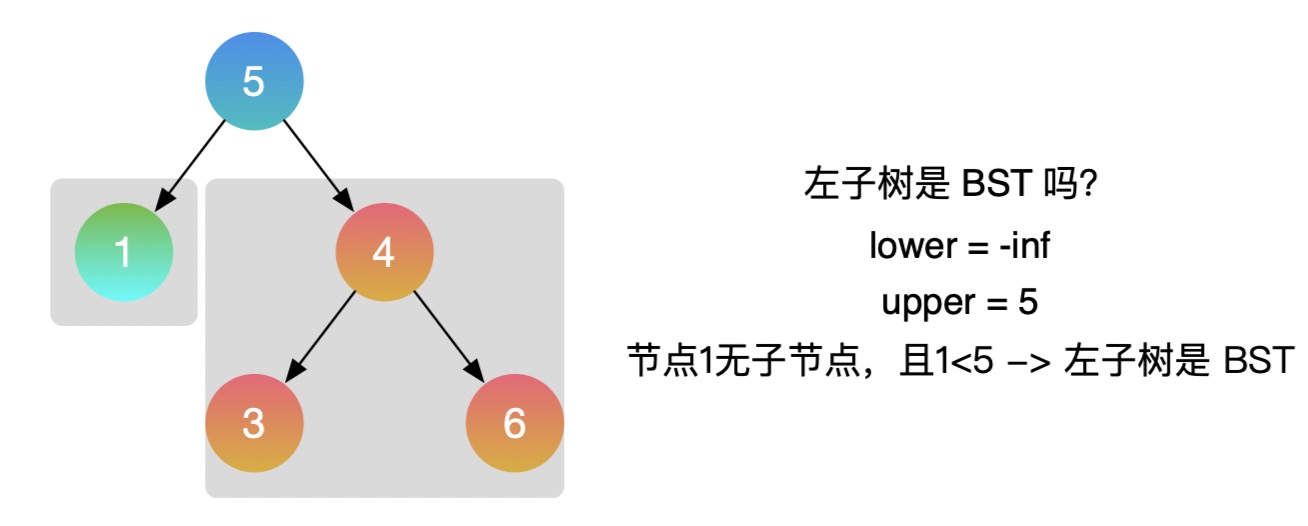
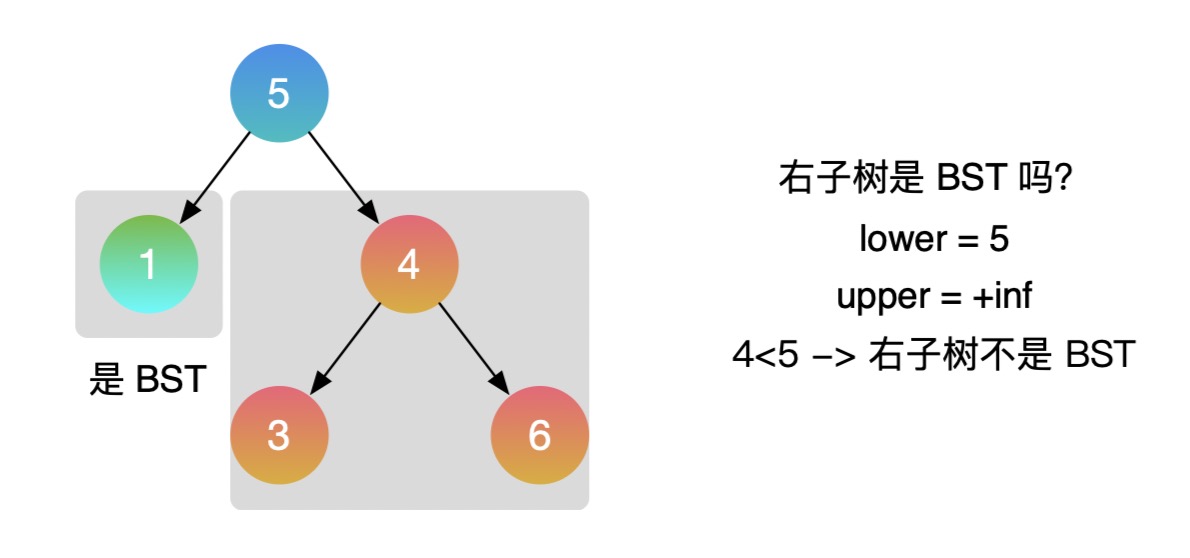
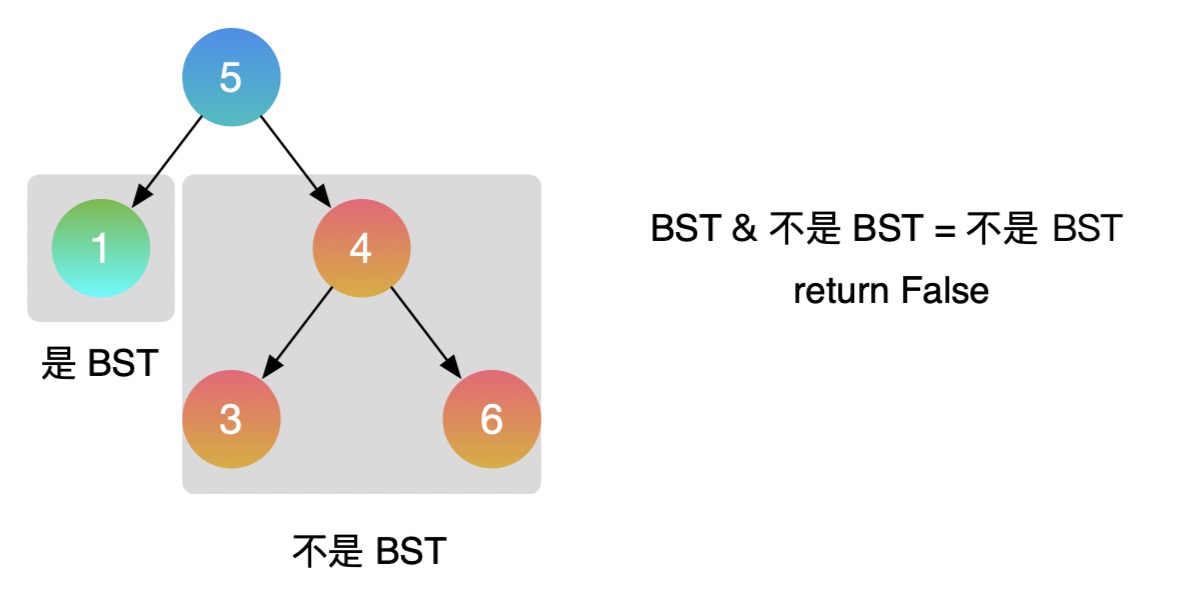
• C + + example:

class Solution {
public:
    bool helper(TreeNode* root, long long lower, long long upper) {
        if (root == nullptr) {
            return true;
        }
        if (root -> val <= lower || root -> val >= upper) {
            return false;
        }
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);
    }
};

• Java example:

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    public boolean isValidBST(TreeNode node, long lower, long upper) {
        if (node == null) {
            return true;
        }
        if (node.val <= lower || node.val >= upper) {
            return false;
        }
        return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);
    }
}

• Middle order traversal:
• • Based on the properties mentioned above, we can further know that the sequence composed of the values obtained from the "middle order traversal" of the binary search tree must be in ascending order, which enlightens us to check whether the value of the current node is greater than the value of the node traversed by the previous middle order in real time. If both are greater than, it means that the sequence is in ascending order, and the whole tree is a binary search tree. Otherwise, it is not. You can use the stack to simulate the process of middle order traversal.
• If you don't know what middle order traversal is, you can simply mention that middle order traversal is an traversal method of binary tree. It first traverses the left subtree, then the root node, and finally the right subtree. The binary search tree ensures that the values of the nodes of the left subtree are less than the values of the root node, and the values of the root node are less than the values of the right subtree. Therefore, the sequence obtained after middle order traversal must be an ascending sequence.
• C + + example:

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> stack;
        long long inorder = (long long)INT_MIN - 1;

        while (!stack.empty() || root != nullptr) {
            while (root != nullptr) {
                stack.push(root);
                root = root -> left;
            }
            root = stack.top();
            stack.pop();
            // If the value of the node obtained from the middle order traversal is less than or equal to the previous inorder, it indicates that it is not a binary search tree
            if (root -> val <= inorder) {
                return false;
            }
            inorder = root -> val;
            root = root -> right;
        }
        return true;
    }
};

• Java example:

class Solution {
    public boolean isValidBST(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        double inorder = -Double.MAX_VALUE;

        while (!stack.isEmpty() || root != null) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
              // If the value of the node obtained from the middle order traversal is less than or equal to the previous inorder, it indicates that it is not a binary search tree
            if (root.val <= inorder) {
                return false;
            }
            inorder = root.val;
            root = root.right;
        }
        return true;
    }
}