Giant shoulders:
https://www.cnblogs.com/onepixel/p/7674659.html
https://visualgo.net/zh/sorting
https://www.runoob.com/w3cnote/merge-sort.html
www.cnblogs.com/binarylei/p/12419863.html
blog.csdn.net/qq_27124771/article/details/87651495
○ summary
| Sorting algorithm | principle | average | worst | space | stability |
|---|---|---|---|---|---|
| Bubble sorting | Adjacent elements are exchanged, and large ones are exchanged to the back [you go up] | O(n²) | O(n²) | O(1) | stable |
| Select sort | Select the largest one from the unsequenced [go to the front of the most dishes] | - | - | - | - |
| Insert sort | Insert a record into the ordered table | - | - | - | - |
| Quick sort | Divide and conquer, find the benchmark [turn the big into the small, and clarify your position according to the standard] | O(nlogn) | O(n²) | O(nlogn) | instable |
| Merge sort | It is the combination of the big and the small, and then the combination of the two | O(nlogn) | O(nlogn) | O(n) | stable |
| Heap sort | Use the maximum heap to pop up to the end [nature of heap] | O(nlogn) | O(nlogn) | O(1) | instable |
| Shell Sort | Insert sort of group [reduce incremental sort] | O(n^1.3) | O(1) | instable | |
| Count sort | The number is used as the subscript of the array [space for time], counting a bucket | O(n) | stable | ||
| Bucket sorting | Improved counting and sorting, one bucket in a range | ||||
| Cardinality sort | Improved counting and sorting, one key value and one bucket |
Average quick sort is the most efficient, but at worst it is not as efficient as heap sort and merge sort
A. Bubble sort (you can do it, you can't do it, don't xxx)
Repeatedly visit the sequence to be sorted, compare two elements at a time, and exchange them if they are in the wrong order. Repeat until there is no need to exchange. Large numbers will float to the back like "bubbles"
graphic
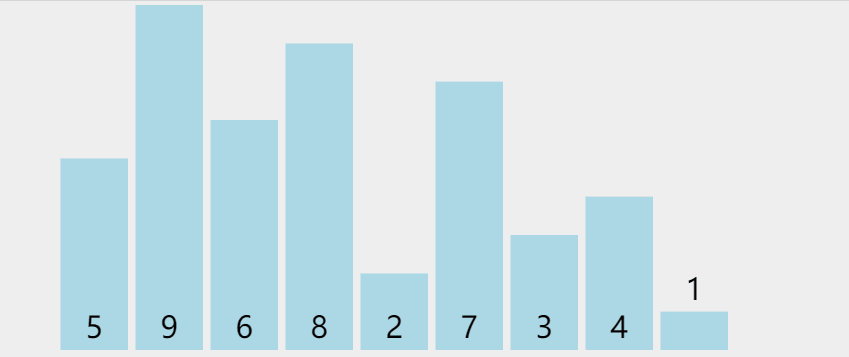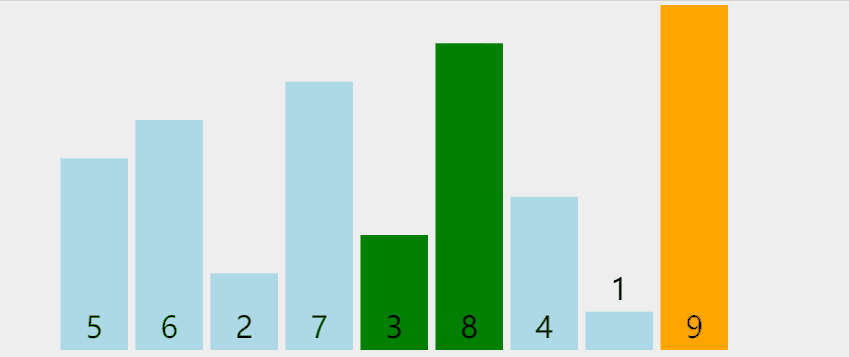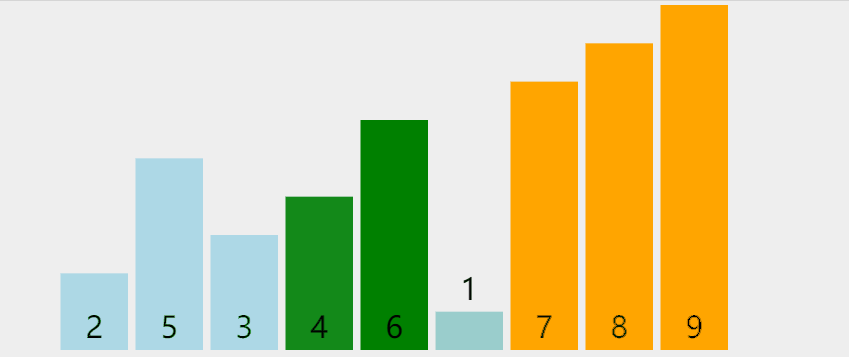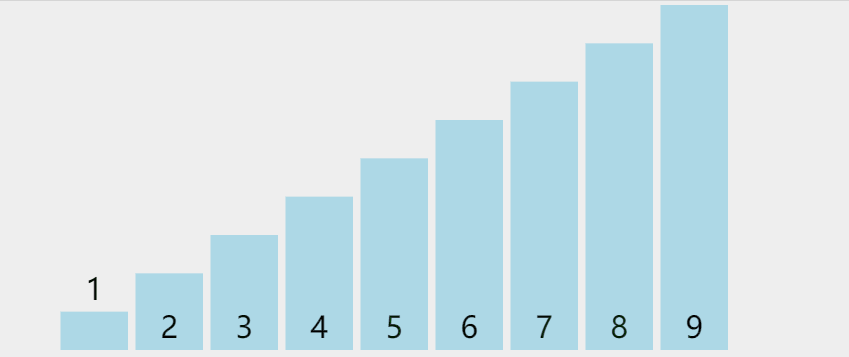
Phased state
loop: 0 list: [5, 6, 8, 2, 7, 3, 4, 1, **9**] loop: 1 list: [5, 6, 2, 7, 3, 4, 1, **8, 9**] loop: 2 list: [5, 2, 6, 3, 4, 1, **7, 8, 9**] loop: 3 list: [2, 5, 3, 4, 1, **6, 7, 8, 9**] loop: 4 list: [2, 3, 4, 1, **5, 6, 7, 8, 9**] loop: 5 list: [2, 3, 1, **4, 5, 6, 7, 8, 9**] loop: 6 list: [2, 1, **3, 4, 5, 6, 7, 8, 9**] loop: 7 list: [1, **2, 3, 4, 5, 6, 7, 8, 9**]
Python language implementation
def BubbleSort(list):
for i in range(len(list)-1): # The outer ring should be compared n-1 times
for j in range(len(list)-i-1): # Pairwise comparison
if list[j]>list[j+1]: # Exchange if the order is wrong
list[j],list[j+1] = list[j+1],list[j]
return list
Implementation of Golang language
func BubbleSort(list []int) []int {
for i := 0; i < len(list)-1; i++ { // External circulation n-1 times
for j := 0; j < len(list)-1-i; j++ {
if list[j] > list[j+1] { // Pairwise comparison
list[j], list[j+1] = list[j+1], list[j] // exchange
}
}
}
return list
}
B. Select and sort (go to the front of the most dishes)
Find the exchange position between the smallest (large) element and the element in the first position in the unordered sequence.
graphic
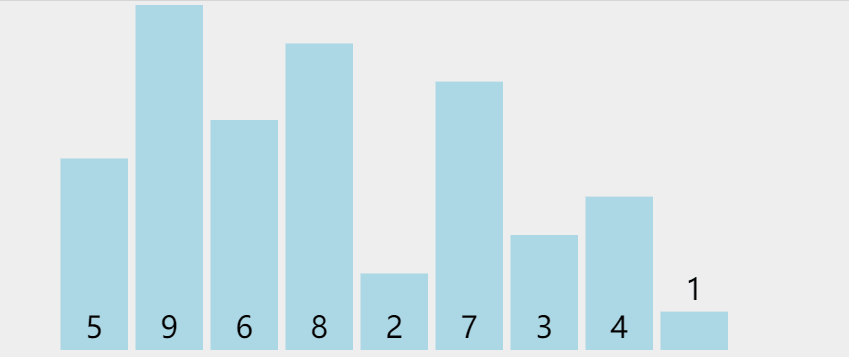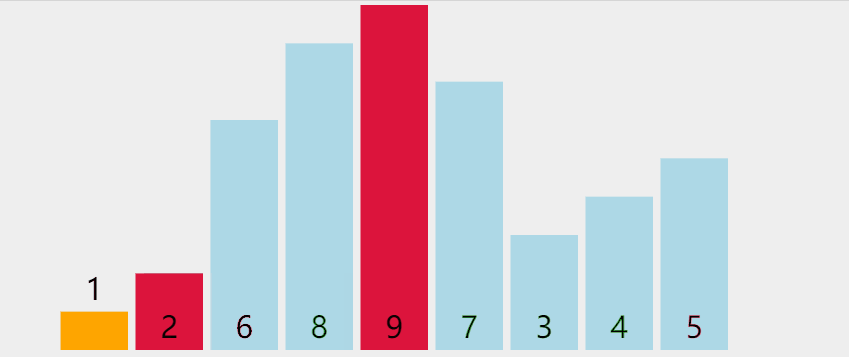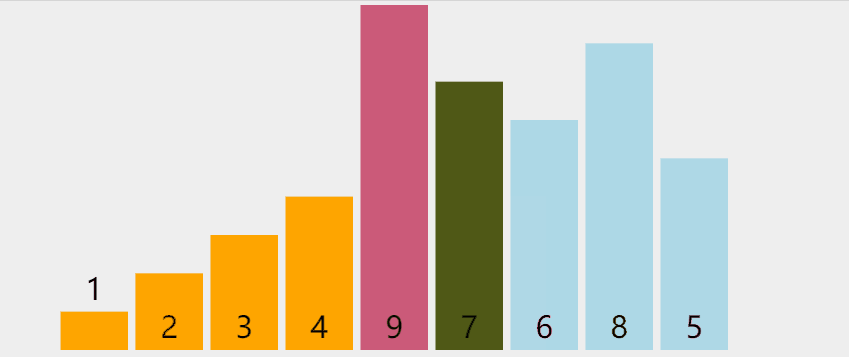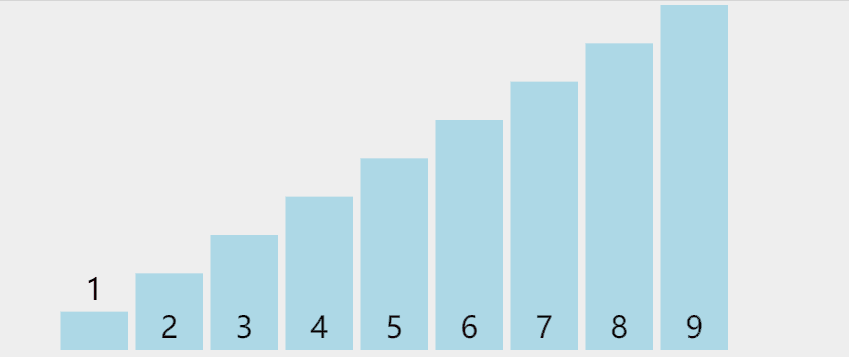
Phased state
loop: 0 list: [**1**, 9, 6, 8, 2, 7, 3, 4, 5] loop: 1 list: [**1, 2**, 6, 8, 9, 7, 3, 4, 5] loop: 2 list: [**1, 2, 3**, 8, 9, 7, 6, 4, 5] loop: 3 list: [**1, 2, 3, 4**, 9, 7, 6, 8, 5] loop: 4 list: [**1, 2, 3, 4, 5**, 7, 6, 8, 9] loop: 5 list: [**1, 2, 3, 4, 5, 6,** 7, 8, 9] loop: 6 list: [**1, 2, 3, 4, 5, 6, 7,** 8, 9] loop: 7 list: [**1, 2, 3, 4, 5, 6, 7, 8**, 9]
Python language implementation
def SelectionSort(list):
for i in range(len(list)-1): # The outer ring should be compared n-1 times
minIndex=i
for j in range(i+1,len(list)): # Remember the position of the smallest one
if list[j]<list[minIndex]:
minIndex=j
list[i],list[minIndex] = list[minIndex],list[i] #exchange
return list
Implementation of Golang language
func SelectionSort(list []int) []int {
for i := 0; i < len(list)-1; i++ { // External circulation n-1 times
minIndex := i
for j := i + 1; j < len(list); j++ { // Find the smallest
if list[minIndex] > list[j] {
minIndex = j
}
}
list[minIndex], list[i] = list[i], list[minIndex] //exchange
}
return list
}
C. Insert sort (poker Management)
By constructing an ordered sequence, for unordered data, scan from back to front in the sorted sequence, find the corresponding position and insert it.
graphic
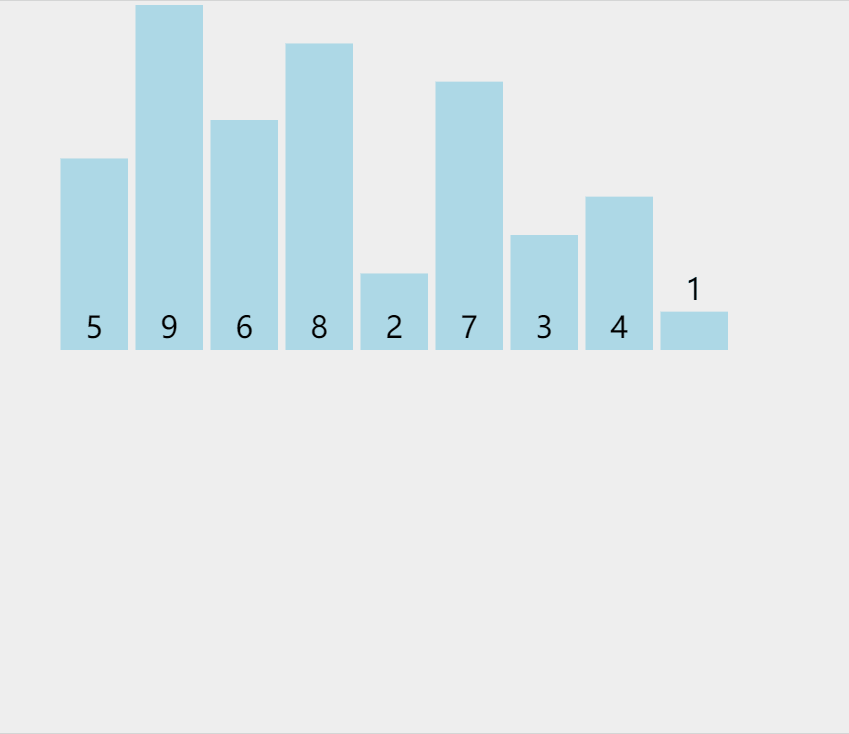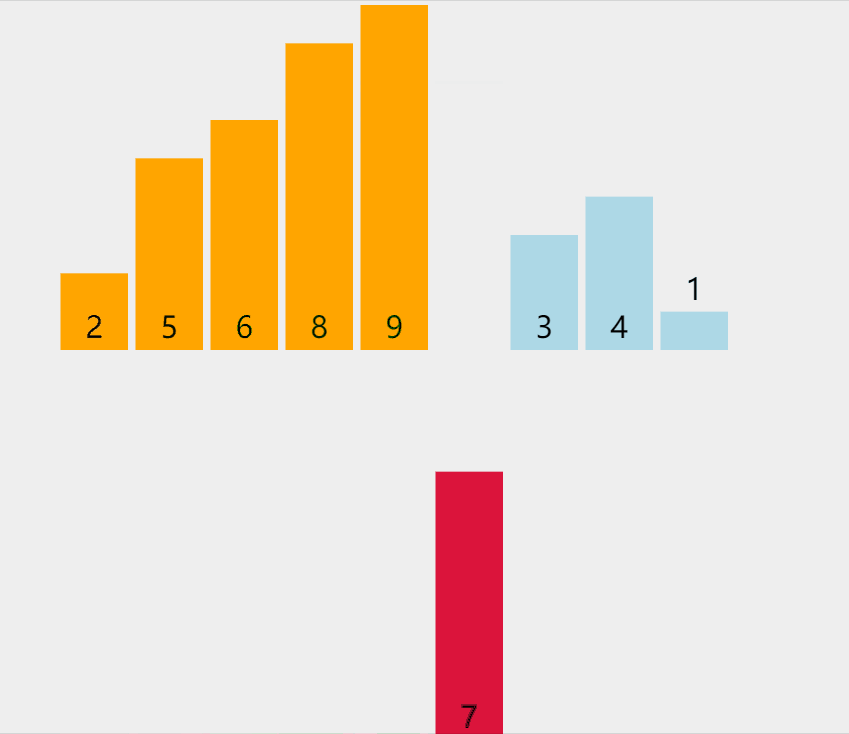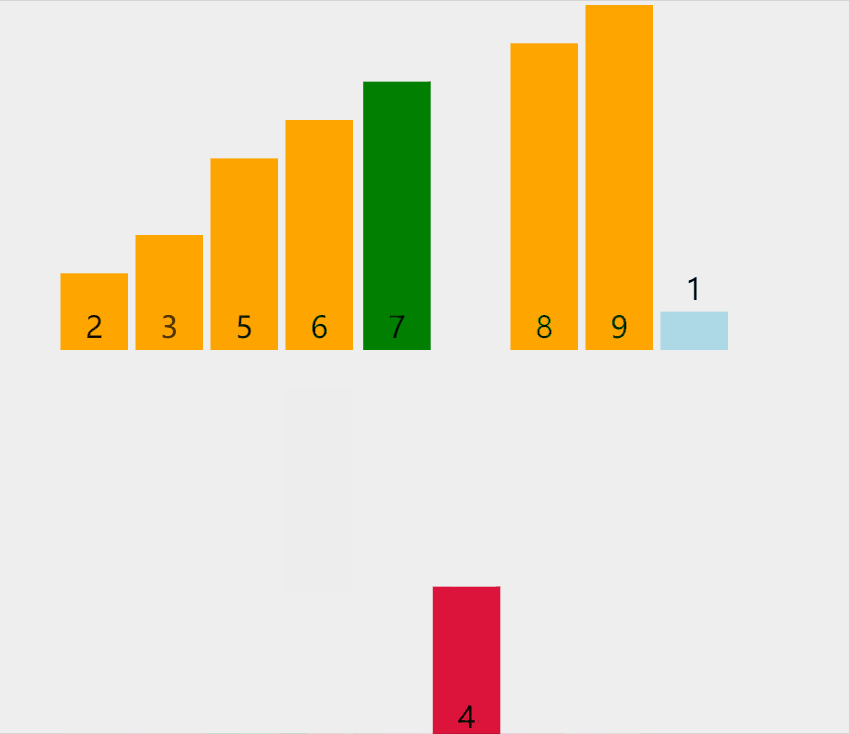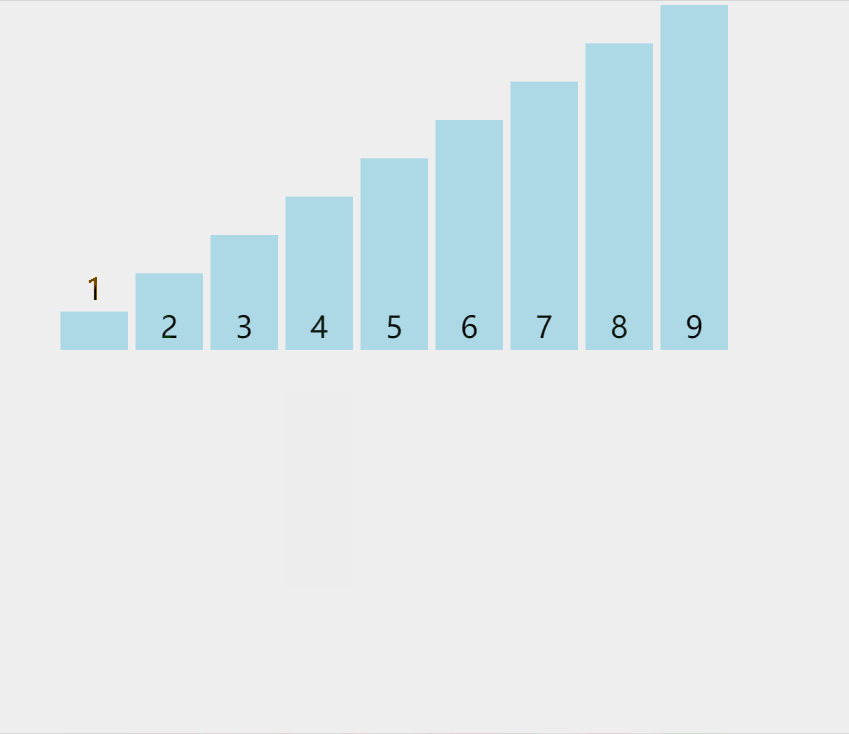
Phased state
loop: 1 list: [5, **9**, 6, 8, 2, 7, 3, 4, 1] loop: 2 list: [5, **6**, 9, 8, 2, 7, 3, 4, 1] loop: 3 list: [5, 6, **8**, 9, 2, 7, 3, 4, 1] loop: 4 list: [2, **5**, 6, 8, 9, 7, 3, 4, 1] loop: 5 list: [2, 5, 6, **7**, 8, 9, 3, 4, 1] loop: 6 list: [2, **3**, 5, 6, 7, 8, 9, 4, 1] loop: 7 list: [2, 3, **4**, 5, 6, 7, 8, 9, 1] loop: 8 list: [**1**, 2, 3, 4, 5, 6, 7, 8, 9]
Python language implementation
def InsertionSort(list):
for i in range(1,len(list)): # The outer ring is not sorted n-1 times
j=i
peakOne = list[i]
while peakOne<list[j-1] and j>0: # Find the insertion position and move back
list[j] = list[j-1]
j-=1
list[j]=peakOne # insert
return list
Implementation of Golang language
func InsertionSort(list []int) []int {
for i := 1; i < len(list); i++ { // External circulation n-1 times
j := i
peakValue := list[i]
for j > 0 && peakValue < list[j-1] { //Find the insertion position and move back
list[j] = list[j-1]
j--
}
list[j] = peakValue //insert
}
return list
}
D. Quick sorting (large to small, according to the benchmark station)
- Pick out an element from the sequence, which is called "pivot";
- Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition exits, the benchmark is in the middle of the sequence. This is called a partition operation;
- Recursively sort the subsequence less than the reference value element and the subsequence greater than the reference value element;
graphic
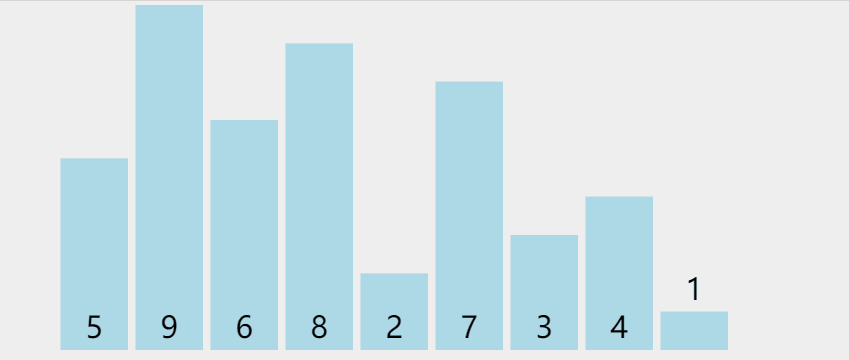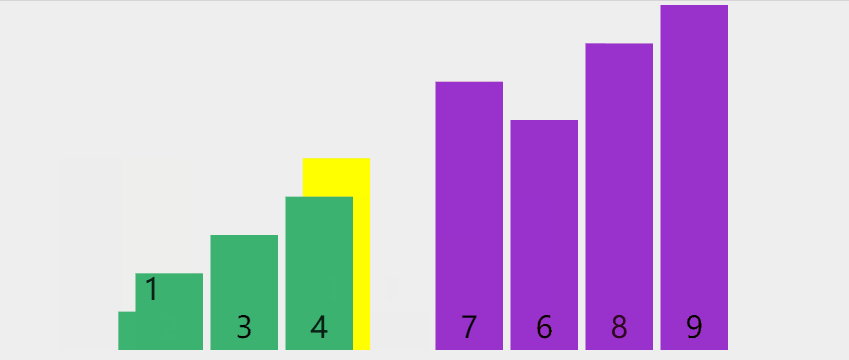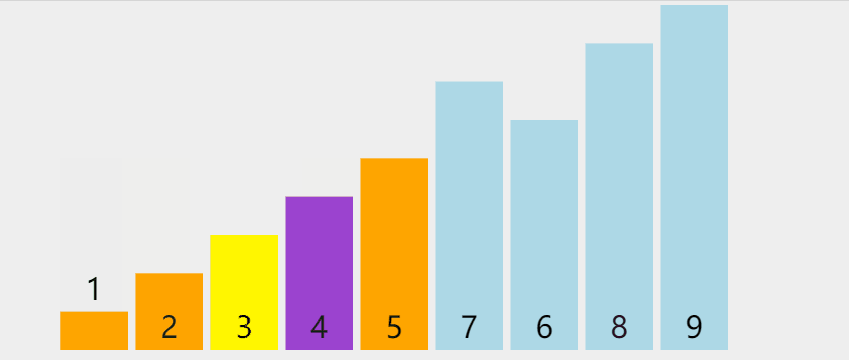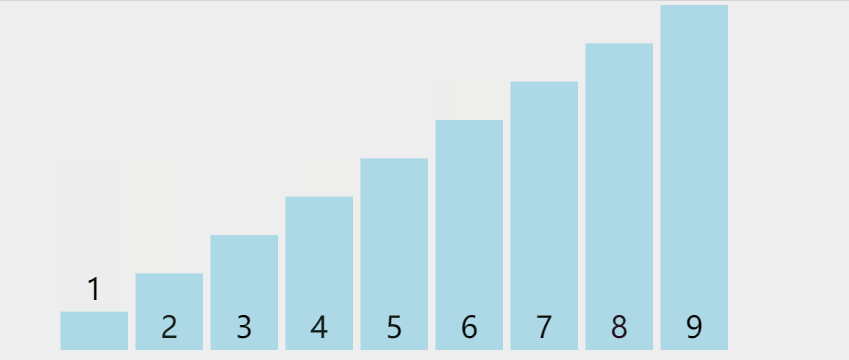
Python language implementation
def QuickSort(list):
def swap(list,i,j):
list[i],list[j]=list[j],list[i]
def partition(list,left,right): # Divide and conquer molecular string
base = list[left] # The datum takes the first one on the left
swapIndex = left+1 # Location for exchange
for i in range(left,right+1): # Traverse the list, find the small one and put it in the front
if list[i]<base:
swap(list,swapIndex,i)
swapIndex += 1
swap(list,left,swapIndex-1) # Insert datum into the middle
return swapIndex-1
def quicksort(list,left,right): # Recursive function
if left >= right: return # Exit condition
mid=partition(list,left,right) # Sort yourself first
quicksort(list,left,mid-1) # Sort left
quicksort(list,mid+1,right) # Sort right
quicksort(list,0,len(list)-1) # Call recursive function
return list
Implementation of Golang language
func swap(list []int, i, j int) {
list[i], list[j] = list[j], list[i]
}
func partion(list []int, left, right int) int {
base := list[left] // Based on the leftmost one
sindex := left + 1 // Swap inserted position
for i := left; i <= right; i++ { // Go through it and convert the small one to the front
if list[i] < base {
swap(list, sindex, i)
sindex++
}
}
swap(list, left, sindex-1) //Insert datum into the middle
return sindex - 1
}
func quicksort(list []int, left, right int) { // Recursive function
if left >= right {
return // Exit condition
}
mid := partion(list, left, right) // Divided into two
quicksort(list, left, mid-1) // Sort left
quicksort(list, mid+1, right) // Sort right
}
func QuickSort(list []int) []int {
quicksort(list, 0, len(list)-1) //Start recursion
return list
}
E. Merge and sort (small and large, keep in order)
- Apply for space so that its size is the sum of two sorted sequences, and the space is used to store the merged sequences;
- Set two pointers, and the initial position is the starting position of the two sorted sequences respectively;
- Compare the elements pointed to by the two pointers, select the relatively small element and put it into the merge space, and move the pointer to the next position;
- Repeat step 3 until a pointer reaches the end of the sequence;
- Copy all the remaining elements of another sequence directly to the end of the merged sequence.
Merge sort vs quick sort
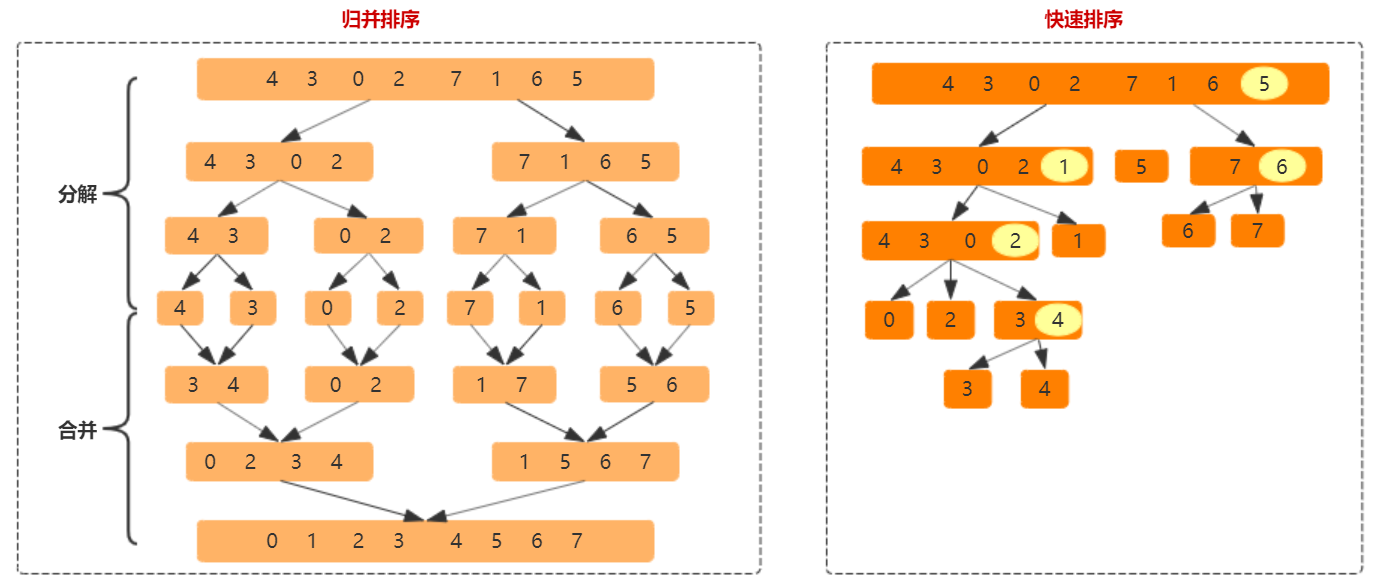
- Merge sort: focus on combination, recursively decompose the sequence into only one element. The core algorithm is the merge function merge: two ordered arrays are still ordered after merging. The merge function determines the spatial complexity and stability of merge sorting.
- Quick read sorting: focus on sorting. Select any element as the partition, which is divided into less than, equal to and greater than three parts, and then sort the less than and greater parts recursively in turn. The core algorithm is the partition function, which divides the sequence into three parts: left, middle and right. The partition function also determines the spatial complexity and stability of quick sorting.
graphic
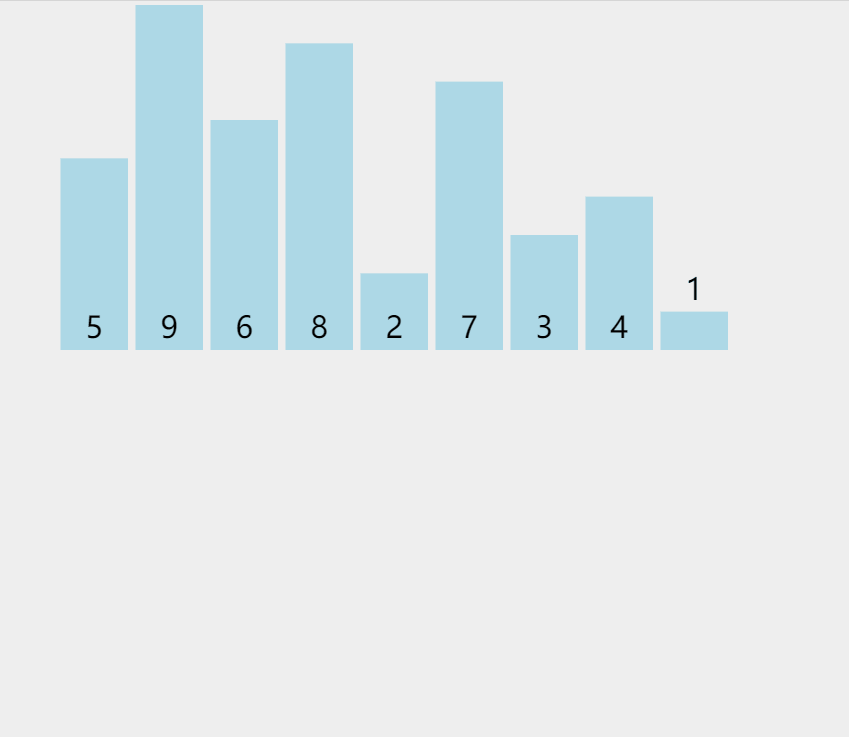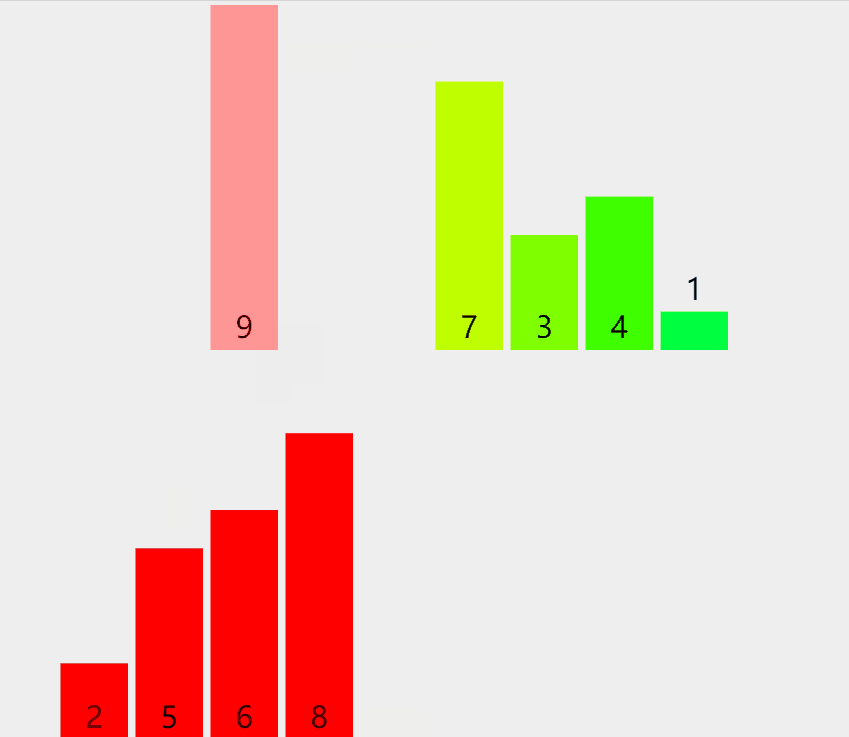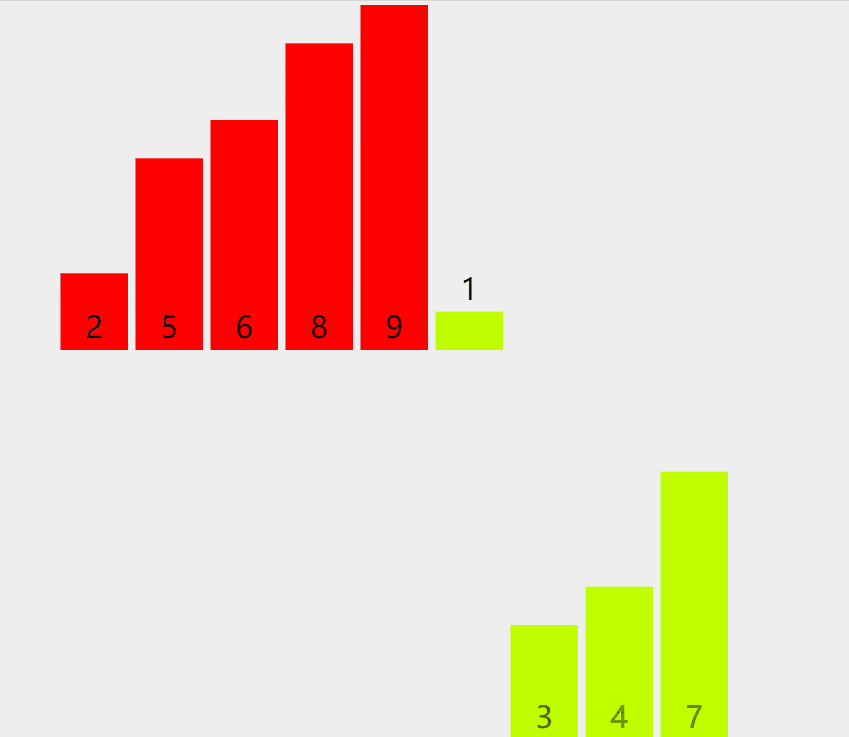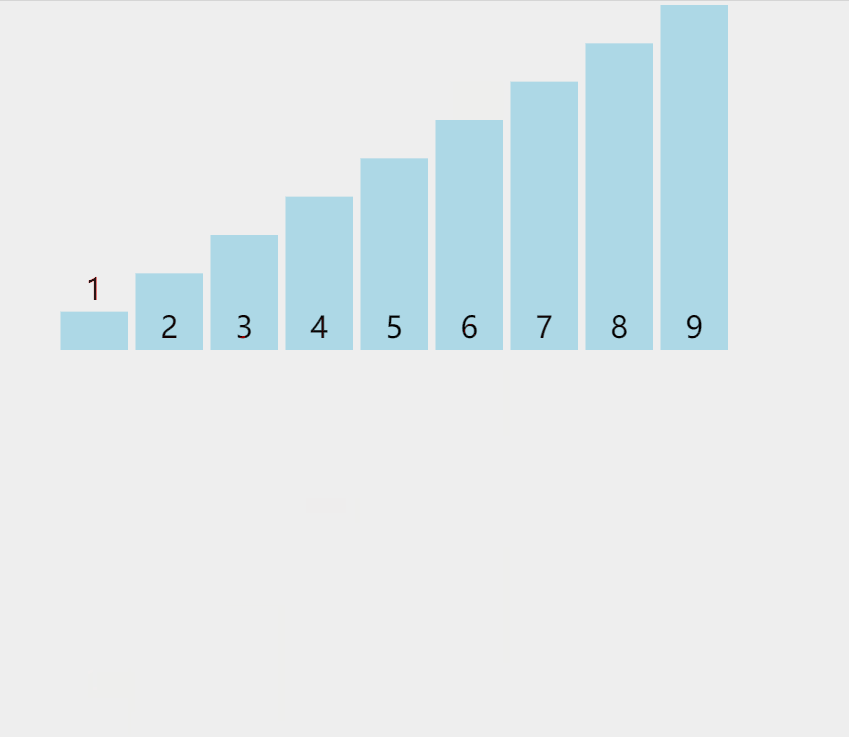
Phased state
[5] + [9] ---> [5, 9] [6] + [8] ---> [6, 8] [5, 9] + [6, 8] ---> [5, 6, 8, 9] [2] + [7] ---> [2, 7] [4] + [1] ---> [1, 4] [3] + [1, 4] ---> [1, 3, 4] [2, 7] + [1, 3, 4] ---> [1, 2, 3, 4, 7] [5, 6, 8, 9] + [1, 2, 3, 4, 7] ---> [1, 2, 3, 4, 5, 6, 7, 8, 9]
Python language implementation
def merge(left,right): # Merge left and right
result=[]
while len(left)>0 and len(right)>0: # Insert by size
if left[0]<right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
while len(left)>0:
result.append(left.pop(0))
while len(right)>0:
result.append(right.pop(0))
return result
def MergeSort(list): # Recursive function
if len(list)<2:
return list # Exit condition
import math
mid = math.floor(len(list)/2) # Split point
left = list[0:mid]
right = list[mid:]
return merge(MergeSort(left), MergeSort(right))
Implementation of Golang language
func merge(left, right []int) []int {
result := make([]int, len(left)+len(right)) //Cache array
mergeIndex := 0
leftIndex := 0
rightIndex := 0
//Insert by size
for leftIndex < len(left) && rightIndex < len(right) {
if left[leftIndex] < right[rightIndex] {
result[mergeIndex] = left[leftIndex]
leftIndex++
mergeIndex++
} else {
result[mergeIndex] = right[rightIndex]
rightIndex++
mergeIndex++
}
}
for leftIndex < len(left) {
result[mergeIndex] = left[leftIndex]
leftIndex++
mergeIndex++
}
for rightIndex < len(right) {
result[mergeIndex] = right[rightIndex]
rightIndex++
mergeIndex++
}
return result
}
func MergeSort(list []int) []int {
if len(list) < 2 {
return list // Exit condition
}
var mid int = len(list) / 2 // Divide into half
return merge(MergeSort(list[0:mid]), MergeSort(list[mid:]))
}
F. Heap sort (nature of heap)
- Selective sorting with heap
- Build heap - > exchange the root node with the last output - > rebuild
- Ascending large top stack
- Small top stack for descending order
graphic

Phased state
init: [9, 8, 7, 5, 2, 6, 3, 4, 1] loop: 8 [8, 5, 7, 4, 2, 6, 3, 1, **9**] loop: 7 [7, 5, 6, 4, 2, 1, 3, **8, 9**] loop: 6 [6, 5, 3, 4, 2, 1, **7, 8, 9**] loop: 5 [5, 4, 3, 1, 2, **6, 7, 8, 9**] loop: 4 [4, 2, 3, 1, **5, 6, 7, 8, 9**] loop: 3 [3, 2, 1, **4, 5, 6, 7, 8, 9**] loop: 2 [2, 1,** 3, 4, 5, 6, 7, 8, 9**] loop: 1 [1, **2, 3, 4, 5, 6, 7, 8, 9**]
Python language implementation
def HeapSort(list):
def down(list,i,len):
while 2*i+1<=len:
l=2*i+1
r=2*i+2 if 2*i+2<len else len
maxChild=max(list[l],list[r]) # The youngest child
if maxChild<list[i]: # The maximum heap property has been satisfied
return
k = l if list[l]==maxChild else r # Maximum child position
list[k],list[i]=list[i],list[k] # Swap parent and child nodes
i=k
#1. Establish initial maximum reactor
for i in range(math.ceil(len(list)-1/2),-1,-1): # Sink each parent node
down(list,i,len(list)-1)
#2. Take vertices in turn and put them in the back
for j in range(len(list)-1,0,-1):
list[j],list[0] =list[0],list[j] # Swap head and tail
down(list,0,j-1)
print("loop:",j," ", list)
return list
Golang implementation
// Node subsidence
func heapDown(list []int, i, len int) {
for 2*i+1 <= len {
left := 2*i + 1 // Left and right child nodes
right := 2*i + 2
if right > len {
right = len // Attention overflow
}
var maxIndex int // Find the largest child node
if list[left] > list[right] {
maxIndex = left
} else {
maxIndex = right
}
if list[maxIndex] < list[i] {
return //The maximum heap property has been satisfied
} else {
list[i], list[maxIndex] = list[maxIndex], list[i]
i = maxIndex
}
}
}
func HeapSort(list []int) []int {
//1. Establish the initial maximum heap
for i := len(list) / 2; i >= 0; i-- { //Start with the last parent node
heapDown(list, i, len(list)-1)
}
//2. Take the pile top to the back in turn
for i := len(list) - 1; i > 0; i-- {
list[i], list[0] = list[0], list[i] //Last
heapDown(list, 0, i-1) //Adjustment reactor
}
return list
}
G. Hill sort (insert improved sort)
- Also called reduced incremental sort
- It is divided into several subsequences for direct insertion sorting, with a certain increment between them
- Insert and sort the whole after it is basically in order
graphic
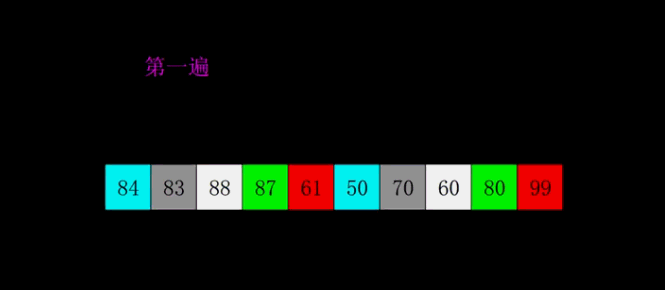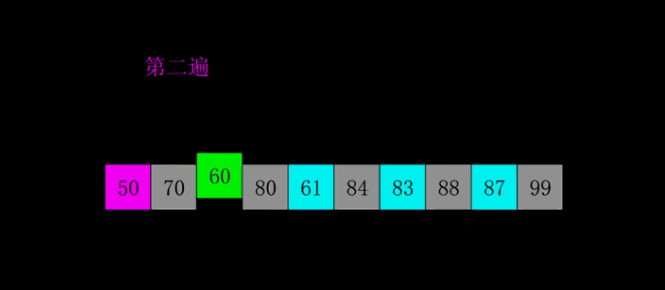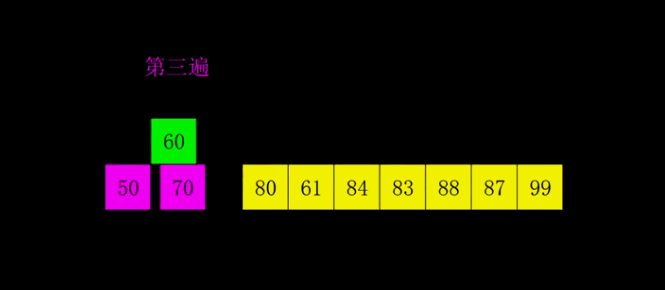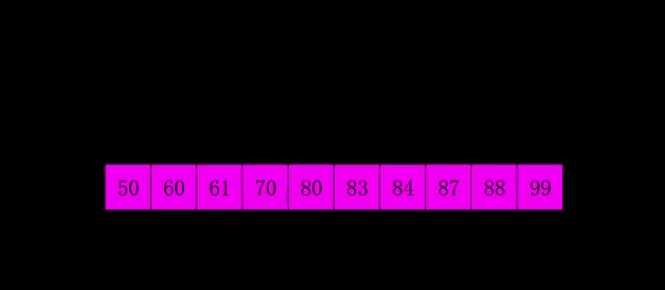
Phased state
gap: 4 [**1**, 7, 3, 4, **2**, 9, 6, 8, **5**] gap: 2 [1, 4, 2, 7, 3, 8, 5, 9, 6] gap: 1 [1, 2, 3, 4, 5, 6, 7, 8, 9]
Python language implementation
def ShellSort(list):
#Hill insert
def shellInsert(list,s,gap):
for i in range(s,len(list),gap):
temp = list[i]
j=i-gap
while j>=0 and list[j]>temp: #Insert at gap intervals
list[j],list[j+gap]=list[j+gap],list[j]
j-=gap
list[j+gap]=temp
gap=int(math.floor(len(list)/2)) #Gradually shrink gap
while gap>0:
for i in range(gap):
shellInsert(list,i,gap)
gap=int(gap/2)
return list
Implementation of Golang language
// Hill inserts with gap as the interval and i as the starting point
func shellInsert(list []int, i, gap int) {
for ; i < len(list); i += gap {
temp := list[i]
j := i - gap
for j >= 0 && temp < list[j] {
swap(list, j, j+gap)
j -= gap
}
list[j+gap] = temp
}
}
// Shell Sort
func ShellSort(list []int) []int {
for gap := len(list) / 2; gap > 0; gap /= 2 {
for i := 0; i < gap; i++ {
shellInsert(list, i, gap)
}
}
return list
}
*//The primary sorting increment is d * void shellinsert (int * a, int d, int len){
int i;
for(int i=d;i<len-1;i++){
int j=i-d;
int temp=a[i];*//Amount moved * while (J > = 0&&a [J] > temp){
a[j+d]=a[j];*//Backward repeat*
j-=d;
}
if(j!=i-d){
a[j+d]=temp;*//Exchange*
}
}
}
*//Hill sort * void Shellsort (int * a, int len){
int d=len/2;*//The initial interval is len/2 * * / / the interval is reduced * while (d > = 1){
ShellInsert(a,d,len);
d/=2;
}
}
H. Count sort (space for time)
-
O(n)
-
Prerequisite: the number with sorting meets a certain range
-
Need space
-
Number as the index of the array
graphic
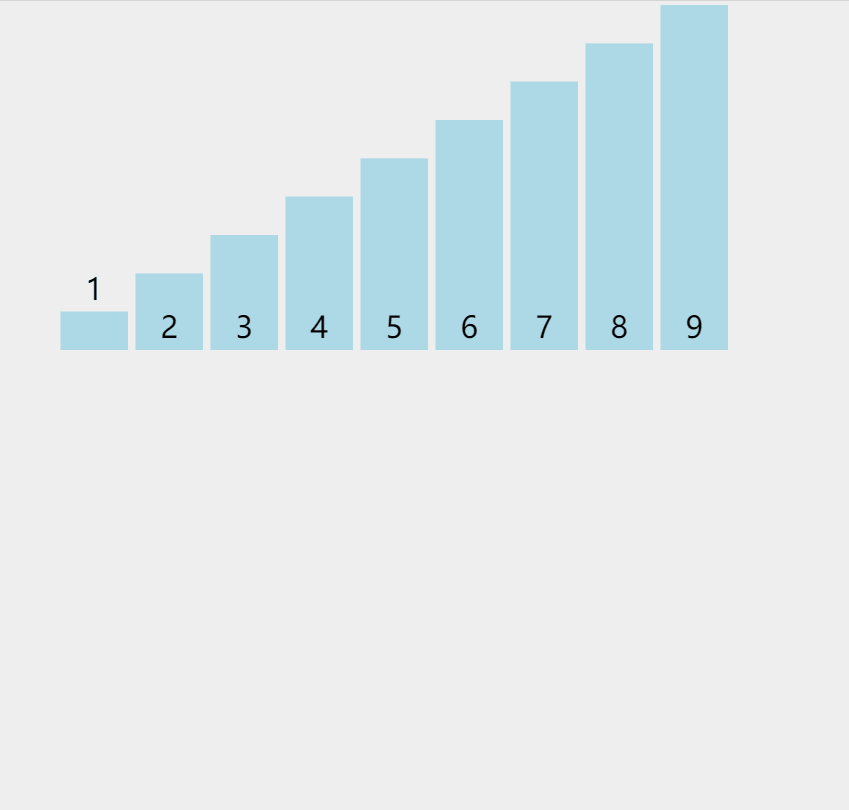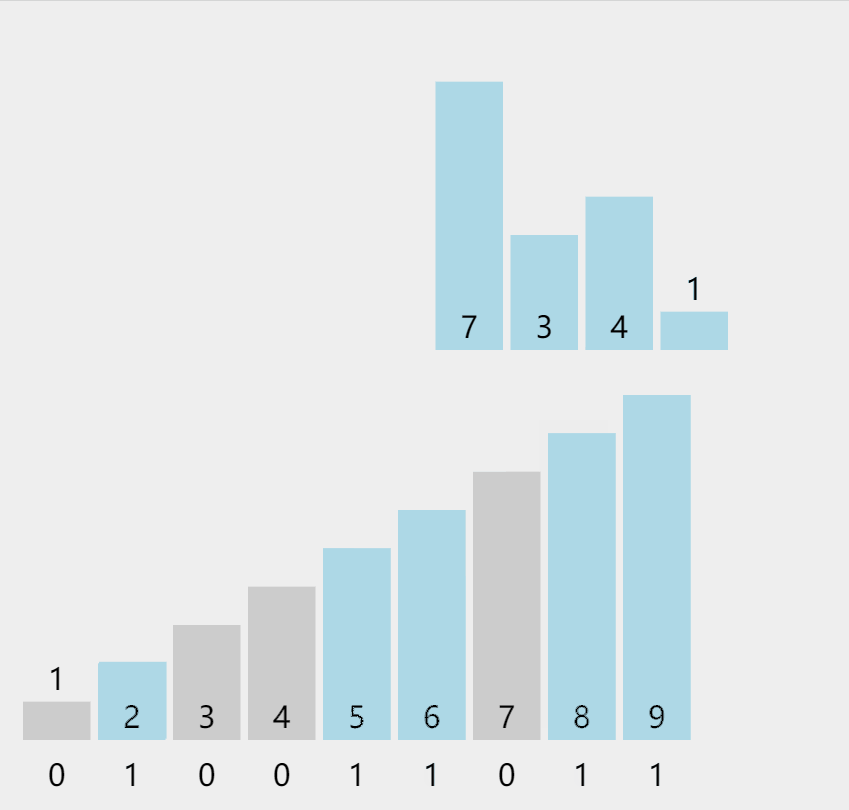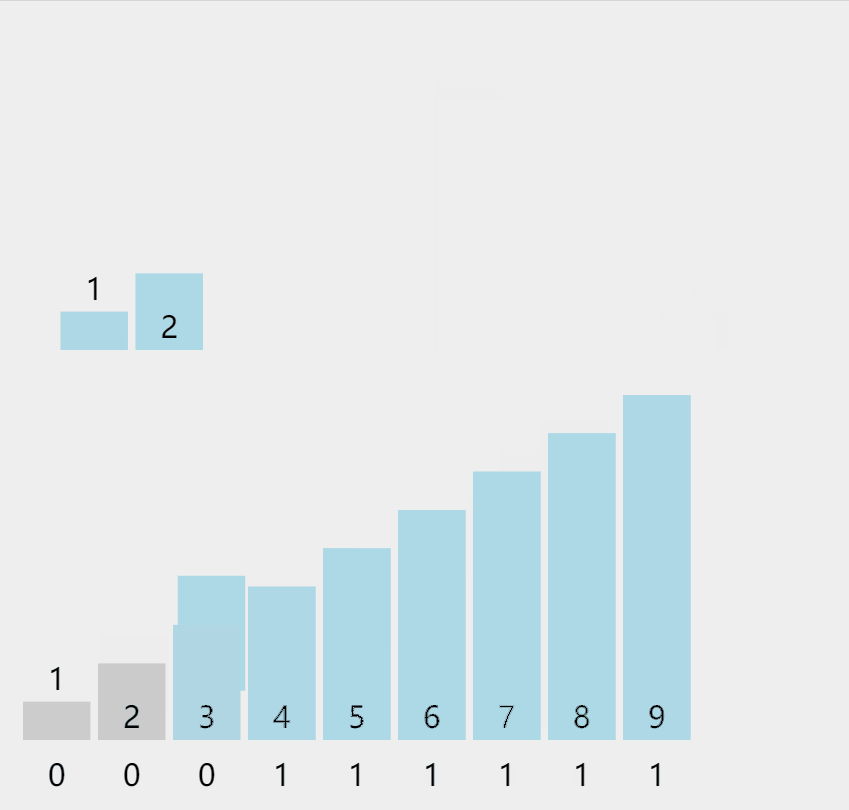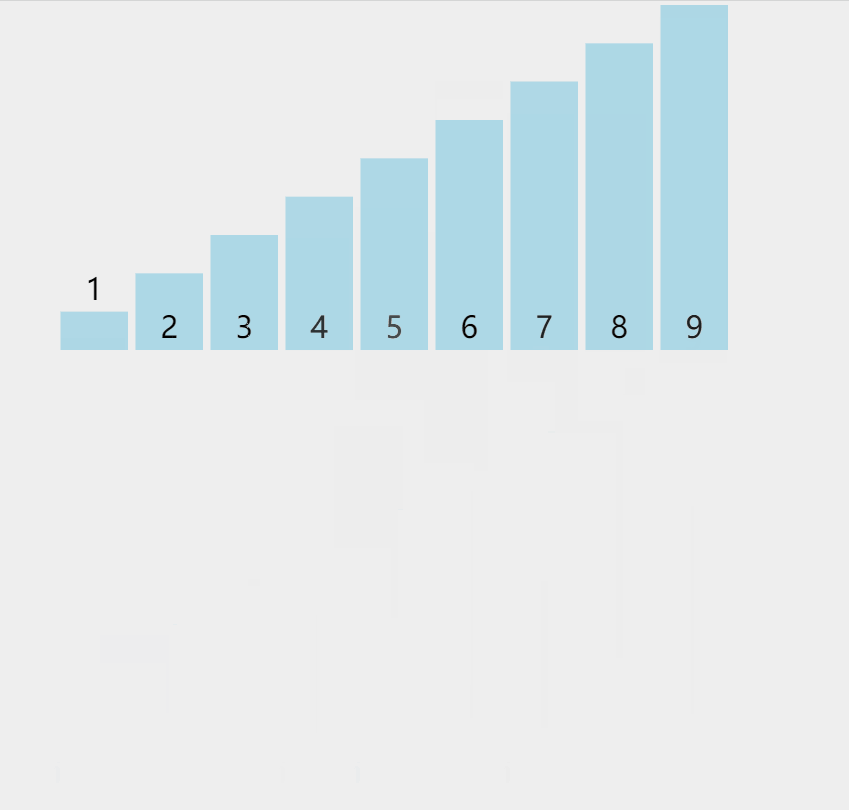
Python language implementation
def CountSort(list):
maxValue=max(list) # Maximum number
Counter =[0 for _ in range(maxValue+1) ] # Counter
for i in list: # Traversal count
Counter[i]+=1
result=[] # Output according to count
for i in range(len(Counter)):
for j in range(Counter[i]):
result.append(i)
return result
Implementation of Golang language
// Count sort
func CountSort(list []int) []int {
// Get maximum
max := list[0]
for i := range list {
if list[i] > max {
max = list[i]
}
}
// container
counter := make([]int, max+1)
// Traversal statistics
for i := range list {
value := list[i]
counter[value]++
}
// Fetch sort
index := 0
for i := range counter {
for j := 0; j < counter[i]; j++ {
list[index] = i
index++
}
}
return list
}
Extension: bucket sorting
Bucket sorting It is an extended version of counting sorting. Counting sorting can be regarded as that each bucket only stores the same elements, while bucket sorting each bucket stores a certain range of elements. Through the mapping function, map the elements in the array to be sorted to each corresponding bucket, sort the elements in each bucket, and finally put the elements in the non empty bucket into the original sequence one by one.

Extension: cardinality sorting
Cut the integer into different numbers according to the number of digits, and then compare them respectively according to each number of digits.
