Tree and binary tree

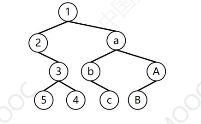
I Trees and forests

• tree: one to many structure (1 to 0, 1 to 1, one to many), with a starting point 'root node'

• node: a data element of the tree

• children: one to many 'many'

• subtree: a tree with a child node as its root

• leaf nodes: nodes without children

• forest: multiple trees

II Binary tree

• binary tree: each node has at most two children (1 or 0), which are called left child and right child respectively

• the left child (if any) is the root of the left subtree and the right child (if any) is the root of the right subtree

• height (depth): the number of layers where the deepest leaf node is located

• important properties of binary tree:

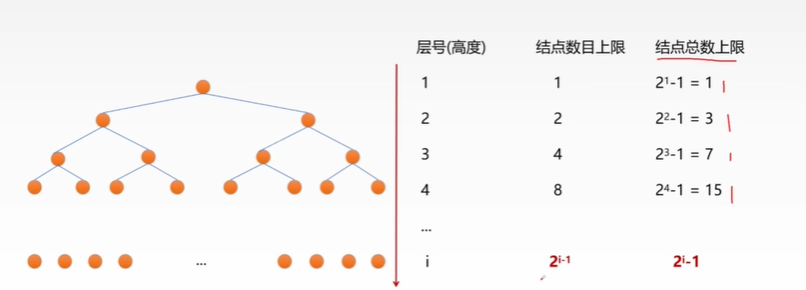
• layer i has at most 2 nodes to the power of i-1

• a tree with height h has at most two nodes to the power of H-1

*key1: each node of binary tree has 0 or 1 or 2 children, and the leaf node has no children

*key2: the height of the binary tree refers to the height from the root node down to the deepest leaf node

1. How many binary trees with different structures can be formed by three nodes? ()

A.2 B.3 C.4 D.5

Analysis: the number of nodes in the left and right subtrees of the root node can be 1-1, 0-2, or 2-0, while the binary tree structure composed of two nodes can only have two kinds, so the answer is 1 + 2 + 2 = 5.

2. If a binary tree has 1025 nodes, its height is ()

A.10 ﹐ B.11 ﹐ C.11 to 1025 ﹐ D.10 to 1025

Analysis: a binary tree with a height of 10 has at mostTherefore, the height is at least 111025 nodes, and at least 1025 layers are extended downward, so the answer is C

Two special binary trees:

• full binary tree:

A full binary tree with a height of h = > 2 to the power of h - 1 nodes

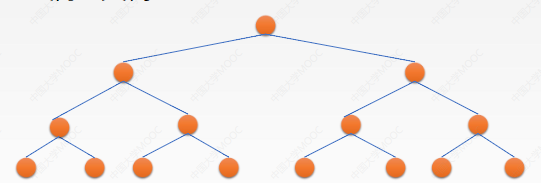
• complete binary tree

It is only vacant on the far right of the lowest floor

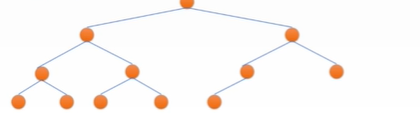
* key1: a full binary tree is full. A complete binary tree is only complete, but not necessarily full

1. If a complete binary tree has 1001 nodes, the number of leaf nodes is ()

A.250 B.254 C.500 D.501

Convert tree / forest to binary tree

• convert tree to binary tree:

• each node only retains the first child (the eldest child) as the left child, and the remaining children (the eldest brother's brothers) are connected to the eldest's right child chain in turn

• forest to binary tree:

1. Each tree is transformed into a binary tree

2. The roots of each tree are connected by a right child chain

give an example:

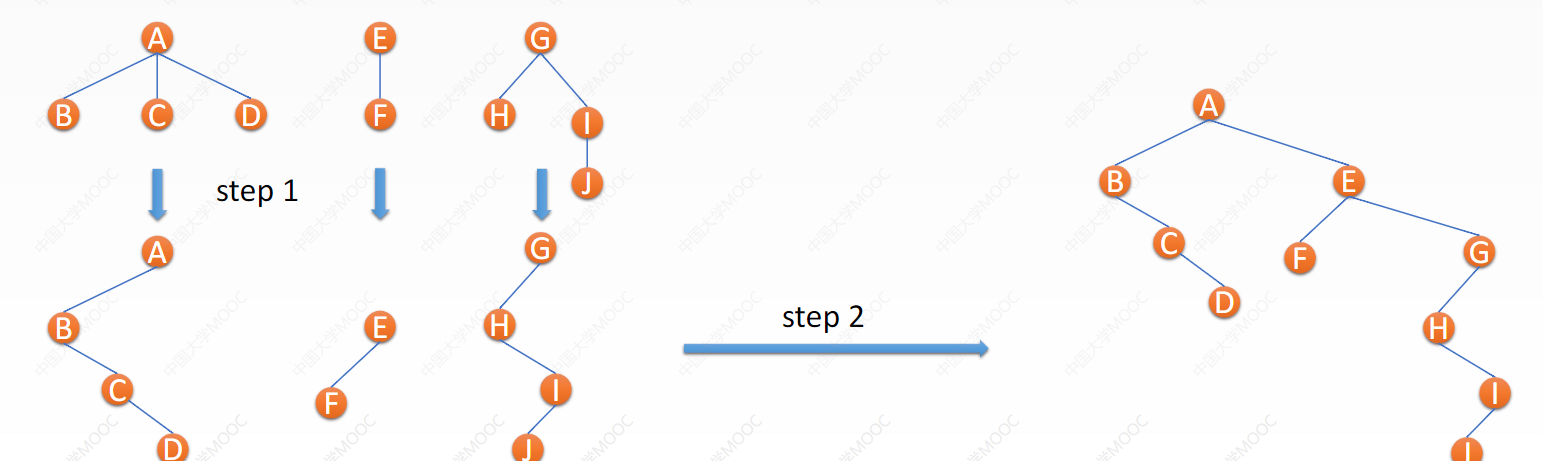
* key1: the transformation from forest to binary tree is a definite and unique process

1. After converting a tree into a binary tree, its form ()

A. B. There are many kinds, C. There are many kinds, but the root node has no right child, D. there are many kinds, but the root node has no left child

Analysis: it is unique, and the root node has no right child

Binary tree sequential storage implementation (logical structure)

• sequential binary tree (array at the bottom)

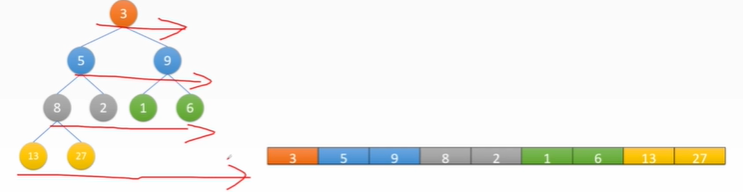
• the left and right children of node i in the sequence tree are 2i+1 and 2i+2 respectively (I counts from 0)

• if the node is empty, it is represented by a special value (such as 0)

Binary tree chain implementation

• linked tree (binary list)

/*Binary tree data structure definition*/
typedef struct TreeNode{
    int data;
    struct    TreeNode *left;
    struct    TreeNode *right;
}TreeNode;

III Traversal of binary tree

• traversal: access all nodes one by one in a certain order (the time complexity is O (n))

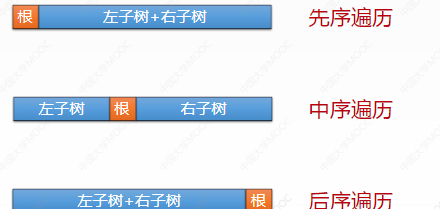
• pre order traversal: current node - left subtree - right subtree

• middle order traversal: left subtree - current node - right subtree

• post order traversal: left subtree - right subtree - current node

• * sequence traversal: traverse each node from left to right layer by layer

• note: the right child is the root of the right subtree and the left child is the root of the left subtree

• note: a tree is represented by its root node, because we can access the whole tree from the root node

Binary tree preorder / inorder / postorder traversal

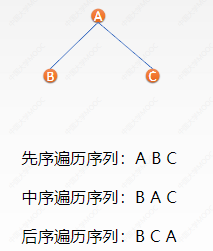
*key1: among the three traversal sequences of binary tree, the left subtree precedes the right subtree. The difference lies in the order of accessing the root

*key2: you can restore the binary tree structure through one of the middle order + first order / second order sequences, but not after + first

1. The preorder traversal sequence of a binary tree is 3541982 and the middle order traversal sequence is 5413892. Please restore its structure

Analysis: the key point of the problem of medium + first / second restore tree structure is that the root node can be determined through the first / second order sequence, and then the left and right subtrees can be divided by traversing the positions of Reagan nodes in the middle order. The problem is reduced to restore the left and right subtrees respectively, and then go down layer by layer until the restoration is completed.

2. Why can't binary trees be restored by pre order + post order sequence?

Analysis: the actual question is why the middle order sequence is necessary to ensure restoration. What important information does the middle order sequence provide?

It provides important information on how to divide the left and right subtrees, but it is impossible to divide the left and right subtrees only by + first

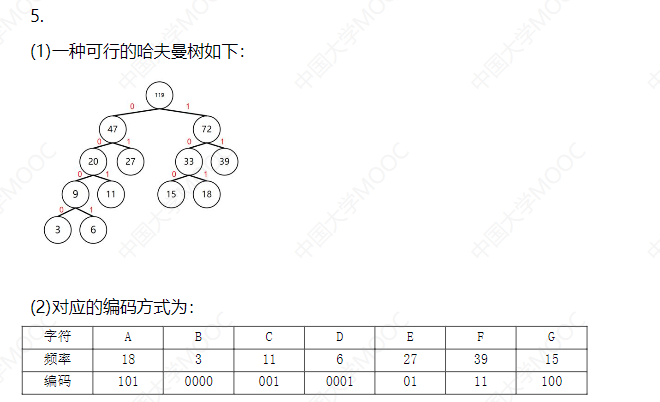
IV Huffman tree

Huffman tree and Huffman coding

• learn how to build a Huffman tree first, and then why there should be a Huffman tree!

• at the beginning of learning, there are a bunch of independent nodes with their own weights

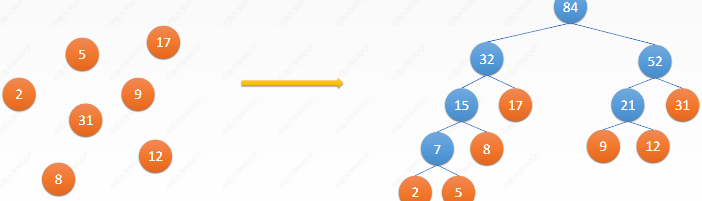
• repeatedly let the two root nodes with the smallest current weight as the left and right children to generate a new root node. The weight of the new node is the sum of their weights until a binary tree is formed

Why Huffman tree?

What are the characteristics of the above process?

• the closer to the root node, the greater the weight

• the initial nodes are all subsequent leaf nodes

• the greater the weight of the leaf node, the closer it is to the root node = > the shorter the path

• what are the benefits? If you mark the path with 0 and 1

• each leaf node has a unique code (variable length)

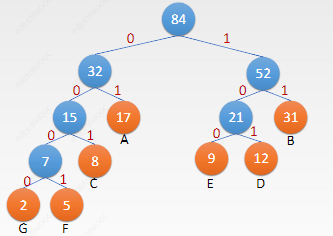
• think: if the weight represents the frequency of occurrence in the article, what are the advantages of this coding?

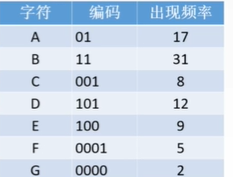
• maximize space savings! The more commonly used character codes, the shorter the length

• this is Huffman coding

• question type: give a character frequency table and construct a Huffman tree to find the Huffman coding table

V code implementation

/*
Binary tree
*/

/* Definition of linked binary tree data structure */
typedef struct TreeNode {
    int data;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

// Note: a tree is represented by its root node, because as long as there is a root node, you can access the whole tree

// Recursive implementation of preorder traversal of binary tree
#include <cstdio>
void PreTraverse(TreeNode *node) {
    if (!node) {
        return;  // Recursive exit
    }
    printf("%d\n", node->data);  // Access the current node first
    PreTraverse(node->left);     // Secondly, recursively traverse the left subtree
    PreTraverse(node->right);    // Finally, the right subtree is traversed recursively
}

// Recursive implementation of order traversal in binary tree
void MidTraverse(TreeNode *node) {
    if (!node) {
        return;  // Recursive exit
    }
    MidTraverse(node->left);     // First recursively traverse the left subtree
    printf("%d\n", node->data);  // Secondly, access the current node
    MidTraverse(node->right);    // Finally, the right subtree is traversed recursively
}

// Recursive implementation of post order traversal of binary tree
void PostTraverse(TreeNode *node) {
    if (!node) {
        return;  // Recursive exit
    }
    PostTraverse(node->left);    // First recursively traverse the left subtree
    PostTraverse(node->right);   // Secondly, the right subtree is traversed recursively
    printf("%d\n", node->data);  // Finally, access the root node
}

// Recursive implementation of finding the height (depth) of the tree
int GetHeight(TreeNode *node) {
    if (!node) {
        return 0;
    }
    int lh = GetHeight(node->left);
    int rh = GetHeight(node->right);
    // Returns the higher height of the subtree around 1 +, where 1 refers to the current node contributing 1 height
    return 1 + (lh > rh ? lh : rh);
}

// Sequence traversal of binary tree (using queue)
#include <queue>
void LevelTraverse(TreeNode *node) {
    if (!node) {
        return;
    }

    std::queue<TreeNode *> q;  // The queue element is a TreeNode*
    q.push(node);
    while (!q.empty()) {
        TreeNode *cur = q.front();  // Get current team leader
        printf("%d\n", cur->data);  // Visit
        q.pop();                    // The team leader left the team
        if (cur->left) {
            q.push(cur->left);  // Left child (if any) join the team
        }
        if (cur->right) {
            q.push(cur->right);  // Right child (if any) join the team
        }
    }
}