Accuracy problems encountered by Golang in dealing with floating point numbers

Golang easy learning

1, What is a floating point number?

Floating point number is a digital representation of the number belonging to a special subset of rational numbers. It is used to approximately represent any real number in the computer. Floating point numbers are mainly used to change the number of floating-point numbers.

Because in the machine language of the computer, there is only binary, and the machine language can only recognize 0 and 1. Therefore, it is impossible for the computer to store decimals, so there needs to be another alternative storage scheme.
This scheme is:

1. Index scheme

Exponential form: its numerical part is a decimal, the number before the decimal point is zero, and the first digit after the decimal point is not zero. A real number can have multiple exponential forms, but only one belongs to the standardized exponential form.

12.3	1.23*10^-1
1.23	1.23*10^0
1.23	0.123*10^1

In the above table, we can clearly understand the index scheme. Similarly, we can also find that there will be a serious problem in expressing decimals in this way, that is, there are too many exponential forms. If the unique form cannot be agreed, there will be problems in the communication between different codes.

2. Standardized index form

1. Among the various representations of exponential form, the representation form in which the number before the decimal point is 0 and the first digit after the decimal point is not 0 is called the standardized exponential form.

The normalized index form of 1.23 is 0.123 * 10 ^ 1

1. A real number has only one normalized exponential form. When a program outputs a real number in exponential form, it must be output in normalized exponential form.

0.123e001

1. Why start with 0

1.23456 needs to store integer part and decimal part respectively for binary storage, while 0.123456 only needs to store decimal part. In this way, the latter method can accommodate floating-point numbers with greater precision when occupying the same byte.

2. Why add 0 after e? Is e001 the same as e1

Adding 0 after it is the output format of% e, which is not necessary for the standardized exponential form,
e001 and e1 are the same

3.IEEE 754 standard

Because there are great differences in the representation of floating-point numbers in different machines, it is not conducive to the transplantation of software between different computers. Therefore, the American IEEE proposed a representation method that supports floating-point numbers from the perspective of system, which is called IEEE754 standard (IEEE, 1985). Almost all popular computers today adopt this standard.

IEEE 754 specifies four ways to represent floating-point values: single precision (32 bits), double precision (64 bits), extended single precision (more than 43 bits, rarely used), and extended double precision (more than 79 bits, usually implemented in 80 bits). Only 32-bit mode has mandatory requirements, and others are optional.

2, Accuracy problems

1. Floating point addition and subtraction

input data:

a = 2.3329 b = 3.1234

The code is as follows (example):

package main

import "fmt"

func main() {

	// a = 2.3329 b = 3.1234
	a, b := 2.3329, 3.1234

	c := a + b

	fmt.Println(c) //5.456300000000001}

}

There is a problem with the accuracy of the results
2.3329 + 3.1234 = 5.456300000000001
An error has occurred

2. Conversion between float64 and float32

input data:

a = 9.99999

The code is as follows (example):

package main

import "fmt"

func main() {

	var a float32
	a = 9.99999

	b := float64(a)
	fmt.Println(b) //9.999990463256836}

}

There is a problem with the accuracy of the results
9.99999 = 9.999990463256836
An error has occurred

3.int64 and float64,int32 and float32 conversion

1.int32 and float32 conversion

input data:

a = 9.99999

The code is as follows (example):

package main

import "fmt"

func main() {

	var a int32
	a = 999990455

	b := float32(a)
	fmt.Printf("%f\n", b) //999990464.000000}

}

There is a problem with the accuracy of the results
999990455= 999990464.000000
An error has occurred

2.int64 and float64 conversion

input data:

a = 999999942424527242

The code is as follows (example):

package main

import "fmt"

func main() {

	var a int64
	a = 999999942424527242

	b := float64(a)
	fmt.Printf("%f\n", b) //999999942424527232.000000}

}

There is a problem with the accuracy of the results
999999942424527242 = 999999942424527232.000000
An error has occurred

4.float64 bit direct multiply by 100

input data:

a = 999999942424527242

The code is as follows (example):

package main

import "fmt"

func main() {

	var a float64
	a = 1128.61

	b := a * 100
	fmt.Println(b) //112860.99999999999}

}

There is a problem with the accuracy of the results
1128.61 * 100= 112860.99999999999
An error has occurred

3, decimal solves the problem of accuracy

Using Decimal package to solve the problem of precision

 go get github.com/shopspring/decimal

1. Floating point addition and subtraction

input data:

a = 2.3329 b = 3.1234

The code is as follows (example):

package main

import (
	"fmt"
	"github.com/shopspring/decimal"
)

func main() {

	// a = 2.3329 b = 3.1234
	a, b := 2.3329, 3.1234

	c := decimal.NewFromFloat(a)
	d := decimal.NewFromFloat(b)
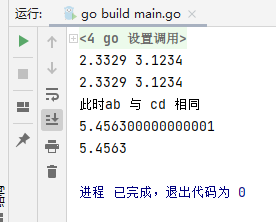
	fmt.Println(a, b)
	fmt.Println(c, d)
	fmt.Println("here ab And cd identical")
	
	fmt.Println(a + b)    //5.456300000000001}
	fmt.Println(c.Add(d)) //5.4563}

}

The accuracy of the results is no longer a problem

2. Conversion between float64 and float32

input data:

a = 9.99999

The code is as follows (example):

package main

import (
	"fmt"
	"github.com/shopspring/decimal"
)

func main() {

	var a float32
	a = 9.99999
	c := decimal.NewFromFloat32(a)
	
	b := float64(a)
	c.Float64()
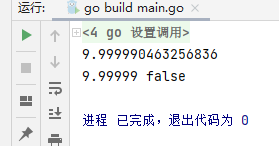
	fmt.Println(b) //9.999990463256836}
	fmt.Println(c.Float64()) //9.99999}

}

The accuracy of the results is no longer a problem

3.float64 bit direct multiply by 100

input data:

a = 999999942424527242

The code is as follows (example):

package main

import (
	"fmt"
	"github.com/shopspring/decimal"
)

func main() {

	var a float64
	a = 1128.61
	c := decimal.NewFromFloat(a)

	b := a * 100
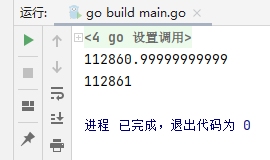
	fmt.Println(b) //112860.99999999999}
	fmt.Println(c.Mul(decimal.NewFromInt(100))) //112861}

}

The accuracy of the results is no longer a problem

summary

Through the above two examples, we have understood the accuracy of floating-point numbers, so we need to change the operation mode in our work. We need to choose Decimal as much as possible. Otherwise, if we use Float and change the method at that time, it will be time-consuming and laborious. It can be solved at the beginning. Why not.

I hope this blog will be beneficial to you. I'm the light king. I speak for myself.