preface
First I did a small project of Gobang, and then I did a more powerful project of Chinese chess, but I never realized a version of "intelligent" AI.
It is well known that the bottom layer of ai algorithm for this kind of game problem is to use minimax search algorithm and α-β Pruning pruning optimization, but I tried it many times and failed to win it....
There are endless blog articles about this kind of algorithm on the Internet, but they are basically very abstract, and then give a pseudo code. The key idea process passes by. I feel that I have said a lot, but in fact I didn't say anything and didn't understand anything. It's not easy to find an article that explained the process clearly, but others just talked about the idea process.
You know, even if you know the flow idea of such a difficult algorithm, you may not be able to write code.
In order to understand this algorithm, people are looking for numbness...
To make complaints about the bad things is to be a yellow sky. If you read more than ten articles, you can finally get the idea and code implementation of the two algorithms.
I believe you all know the basic background and content of these two algorithms. I won't talk about them. Now I'll lead you straight to the topic.
minimax algorithm
This time, I will not talk about it in the usual way. First, I will give the code directly. If you can fully understand it, you can skip this section directly. After all, your own understanding will be better than others with your own understanding.
Complete code
const minimax = (player, node) => {
if (!node.value) {
const map = [];
node.children.forEach(child => {
map.push(minimax(player ^ 1, child));
});
node.value = player === 1 ? Math.max(...map) : Math.min(...map);
}
return node.value;
}
You're right. The minimax search algorithm has only a few lines of code.
If you can't understand these lines of code, let me take you to understand.
Algorithmic thought
First, let's look at a practical problem:
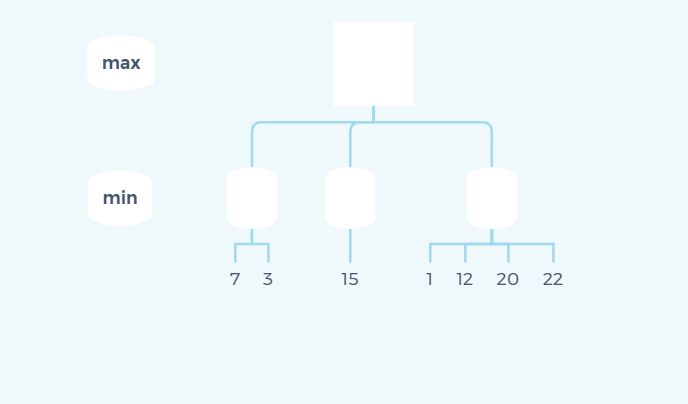
As shown in the figure above, find the final result of max.
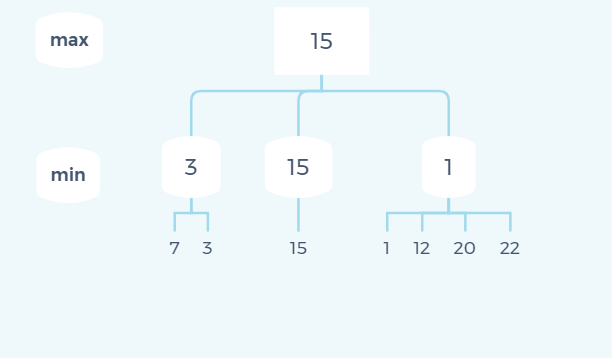
It's not hard to find. The final solution process is shown in the figure above, and the result is 15
The core idea of minimax search is to find the maximum result in the odd layer and the minimum result in the even layer.
Minimax search is to find the most favorable result for yourself in the current layer. Then in the next round of search, the other party will also find the most favorable result for him (that is, the most powerless result for himself), so the final result is the most favorable result for both sides.
code implementation
Next, let's take this example to see the implementation of the code:
// 1:max 0:min
const minimax = (player, node) => {
// If it is not the bottom layer, continue to recurse all child elements
if (!node.value) {
const map = [];//Collect all results of the current layer
node.children.forEach(child => {
map.push(minimax(player ^ 1, child));
});
// The max or min operation is determined according to the current player
node.value = player === 1 ? Math.max(...map) : Math.min(...map);
}
// The result of the child element is returned to the parent element
return node.value;
}
function main(tree) {
const res = minimax(1, tree);
console.log(res);
console.log(tree);
}
const tree1 = {
value: null,
children: [
{
value: null,
children: [
{
value: 7,
children: []
},
{
value: 3,
children: []
}
]
},
{
value: null,
children: [
{
value: 15,
children: []
}
]
},
{
value: null,
children: [
{
value: 1,
children: []
},
{
value: 12,
children: []
},
{
value: 20,
children: []
},
{
value: 22,
children: []
}
]
},
]
}
main(tree1);
Running the above code, we can get the expected minimax search results and the complete search tree.
In fact, minimax search is a recursive idea similar to backtracking, but we only retain one result in each layer, and the retention method of the result depends on the parity of the current level.
Through the above algorithm ideas and code comments, I believe you should be able to fully master the minimax algorithm this time.
Algorithm optimization
Looking at the above case, it is not difficult for us to find that when we are in the third 1 of the third branch, it is not necessary to continue to traverse the subsequent 12, 20 and 22 nodes. Because the upper layer is the min layer, the result will not exceed 1, and there are already 15 nodes in the same layer, so the current branch can be pruned, and this optimization idea is α-β Pruning algorithm.
α-β Pruning algorithm
Complete code
Similarly, I'll give you the complete code first. Let's try whether we can understand it by ourselves.
const alphaBeta = (player, node, alpha, beta) => {
if (!node.value) {
const map = [];
for (let i = 0; i < node.children.length; i++) {
const val = alphaBeta(player ^ 1, node.children[i], alpha, beta);
map.push(val);
if (player === 1) {
if (val > alpha) {
alpha = val;
}
if (alpha >= beta) {
return alpha;
}
} else {
if (val < beta) {
beta = val;
}
if (alpha >= beta) {
return beta;
}
}
}
node.value = player === 1 ? Math.max(...map) : Math.min(...map);
}
return node.value;
}
You're right. It's optimized based on minimax search α-β The pruning algorithm is only a few more lines of logic code.
But it is these lines of code that make the minimax search of its understanding difficulty and foundation not at the same level.
Algorithmic thought
α-β In fact, the idea of pruning algorithm has been mentioned in the optimization part of minimax algorithm, but the description there is incomplete.
Now I try to describe it completely according to my own understanding:
Minimax search is an idea of recursive traversal of dfs. At present, it is only to obtain the top result. Therefore, we might as well default to an initial interval range for the top result, that is( α,β) (generally from negative infinity to positive infinity), then when we do not recursively traverse a branch, we will update the interval range according to the feedback results, and bring this interval range into the recursion of subsequent branches. If the results obtained from the sub branches of subsequent branches do not meet this interval, you can completely give up and continue to recursively traverse the whole branch, that is α-β prune.
The difficulty here lies in the connection between nodes( α,β) Here are a few specific cases.
Case 1: it's still the above example, but it's used this time α-β Ideas of pruning algorithm
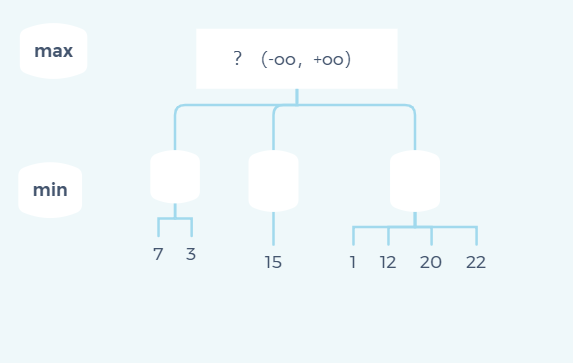
First, when we get result 7 at the first node of min layer, we will get the following state diagram:
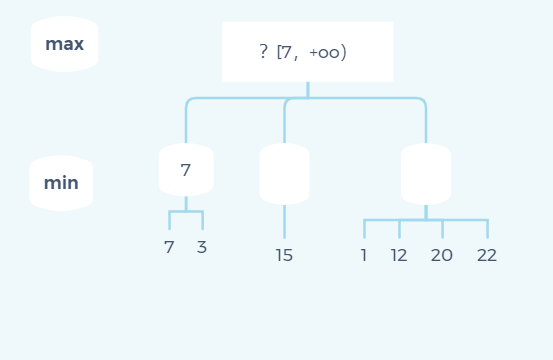
That is, through the first branch, we can determine the lower bound α In the same way, when recursively traversing the second node, we get the following state diagram:
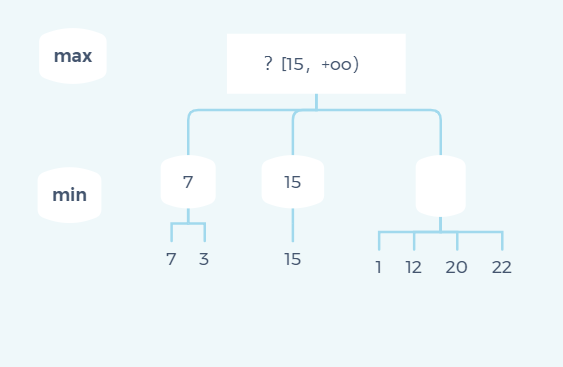
All the above are normal. Now when you traverse to the first child node 1 of the third node, you can stop traversing the third node.
You can see the following state diagram: (the current branch of the enclosed digital code is pruned)
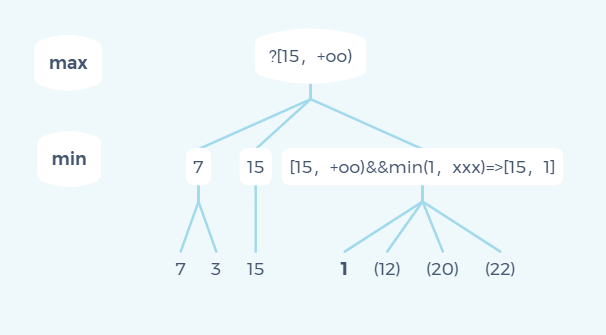
The parent element notifies its lower bound α It should be greater than 15, but one of them is the sub result 1, that is, it is doomed that the upper bound of the current node is 1 and the lower bound 15 is greater than the upper bound 1. Therefore, the current node can give up completely, that is, there is no need to continue to traverse the values of subsequent sub nodes, and the traversal of three sub branches is reduced in an instant.
Have you found something, but this example is too simple and not interesting. Let's change a more complex example:
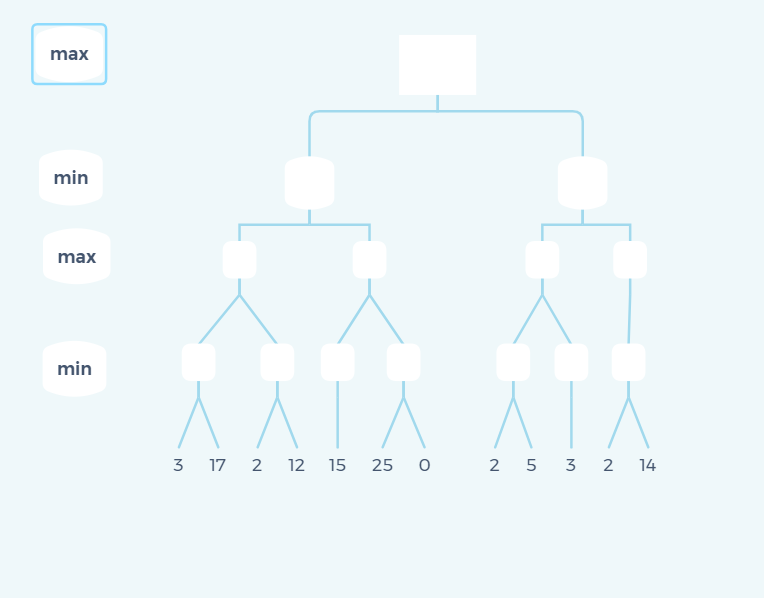
This case is much more complicated. Let's try to think about it by ourselves. I won't show all the details this time. I only show the state when pruning occurs.
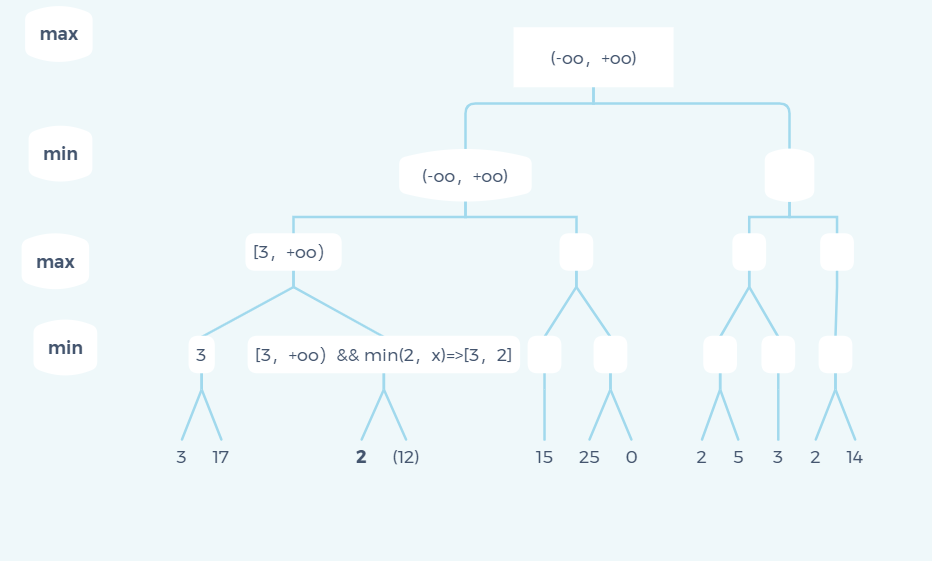
The first place where pruning will be performed is that when traversing 2 in the graph, its parent node will produce [3,2] a situation where the lower bound is greater than the upper bound, so the following 12 child nodes will be pruned.
There are also three places that have been pruned:
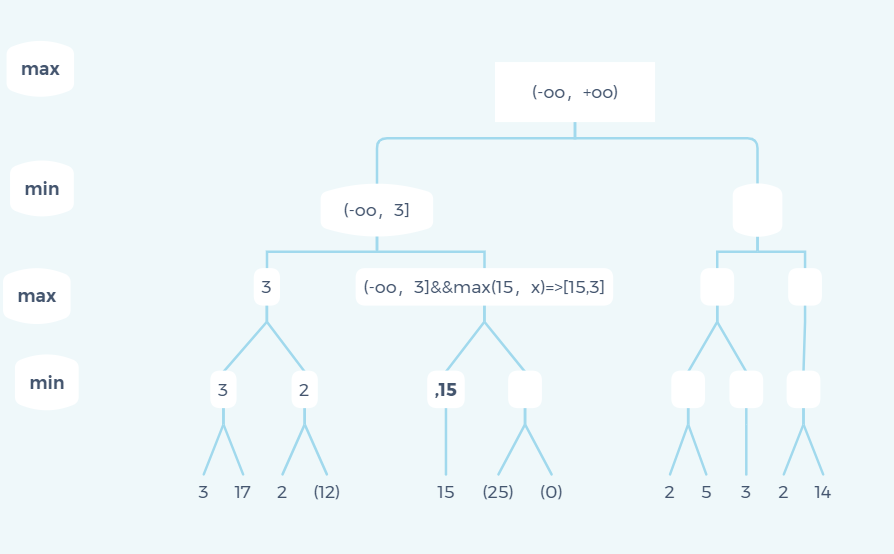
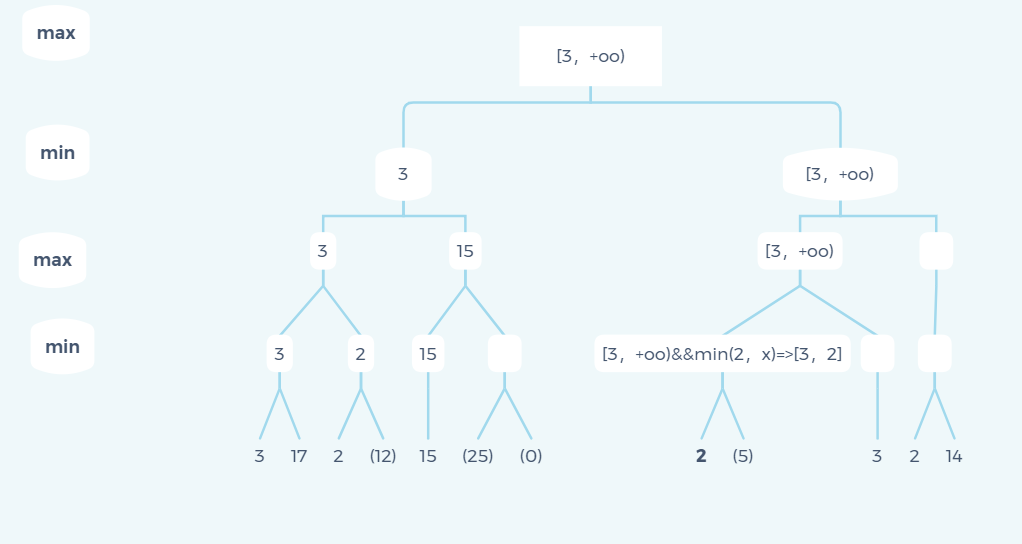
Some friends may wonder why the state of the other branch [3, + oo) of the graph can always be passed to the child elements. Here I explain:
The result 3 has been obtained in the first large branch. If there is any branch with data less than 3 in the other branch, whether in the max layer or the min layer, this branch is actually a useless branch (you can understand this place carefully).
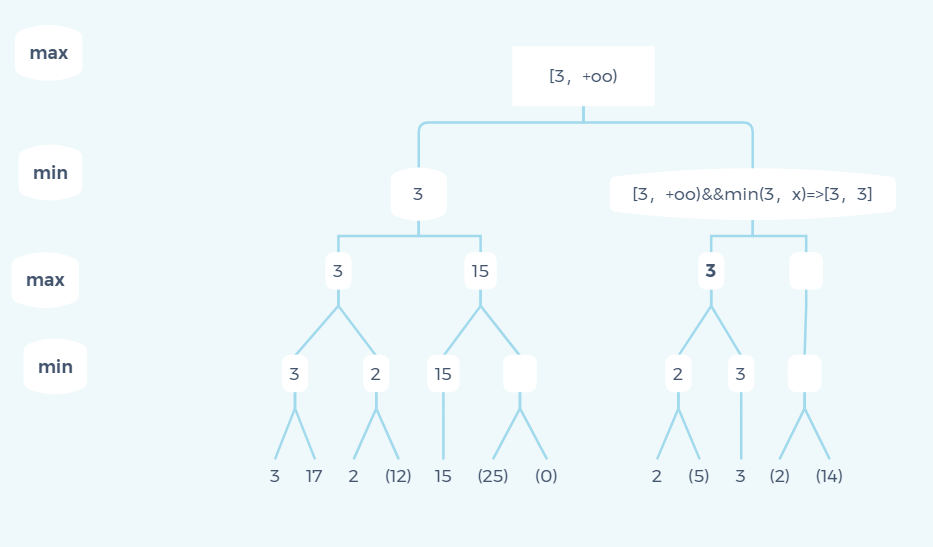
In the last place, if the upper bound is equal to the lower bound, the subsequent branches do not need to traverse, because the value that the current node can return is either the fixed value or no solution.
Through the above cases, it is not difficult for us to find out α-β The core of pruning is to update the upper and lower bounds of nodes recursively, so as to achieve the effect of pruning.
It can be summarized as the following four points:
- The value of the sub element of the max layer is greater than the current lower bound, and the lower bound is updated
- If the lower bound of max layer is greater than or equal to the upper bound, it will directly return to the lower bound (return the larger one), that is, pruning
- The upper bound is updated when the value of the min layer sub element is less than the value of the current upper bound
- The lower bound of min layer is greater than or equal to the upper bound, and directly returns to the upper bound (the smaller one), that is, pruning
code implementation
Based on the minimax search algorithm, combined with the above four points α-β The following code can be obtained by pruning the core:
//[alpha,beta]
const alphaBeta = (player, node, alpha, beta) => {
if (!node.value) {
const map = [];
for (let i = 0; i < node.children.length; i++) {
const val = alphaBeta(player ^ 1, node.children[i], alpha, beta);
map.push(val);
// The result of the last child element changes the alpha beta of the parent element and brings the updated alpha beta into the recursion of subsequent child elements
if (player === 1) {
// The value of the sub element of the max layer is greater than the current lower bound, and the lower bound is updated
if (val > alpha) {
alpha = val;
}
// If the lower bound of max layer is greater than or equal to the upper bound, it will directly return to the lower bound (return the larger one)
if (alpha >= beta) {
return alpha;
}
} else {
// The upper bound is updated when the value of the min layer sub element is less than the value of the current upper bound
if (val < beta) {
beta = val;
}
// If the lower bound of min layer is greater than or equal to the upper bound, return to the upper bound directly (return the smaller one)
if (alpha >= beta) {
return beta;
}
}
}
// Returns the extreme value of the current layer node for pruning the parent element (not alpha or beta)
node.value = player === 1 ? Math.max(...map) : Math.min(...map);
}
return node.value;
}
function main(tree) {
const res = alphaBeta(1, tree, Number.MIN_SAFE_INTEGER, Number.MAX_SAFE_INTEGER);// Number. MIN_ There is a bug when the value is directly compared
console.log(res);
console.log(tree);
}
const tree1 = {
value: null,
children: [
{
value: null,
children: [
{
value: 7,
children: []
},
{
value: 3,
children: []
}
]
},
{
value: null,
children: [
{
value: 15,
children: []
}
]
},
{
value: null,
children: [
{
value: 1,
children: []
},
{
value: 12,
children: []
},
{
value: 20,
children: []
},
{
value: 22,
children: []
}
]
},
]
}
main(tree1);
Running this code can get the same result as the minimax search algorithm.
Algorithm comparison
Next, I will add something to the two algorithms to make the optimization effect of the algorithm more obvious.
let countMinimax = 0;
let countAlphaBeta = 0;
// 1:max 0:min
const minimax = (player, node) => {
countMinimax++;
// If it is not the bottom layer, continue to recurse all child elements
if (!node.value) {
const map = [];//Collect all results of the current layer
node.children.forEach(child => {
map.push(minimax(player ^ 1, child));
});
// The max or min operation is determined according to the current player
node.value = player === 1 ? Math.max(...map) : Math.min(...map);
}
// The result of the child element is returned to the parent element
return node.value;
}
//[alpha,beta]
const alphaBeta = (player, node, alpha, beta) => {
countAlphaBeta++;
if (!node.value) {
const map = [];
for (let i = 0; i < node.children.length; i++) {
const val = alphaBeta(player ^ 1, node.children[i], alpha, beta);
map.push(val);
// The result of the last child element changes the alpha beta of the parent element and brings the updated alpha beta into the recursion of subsequent child elements
if (player === 1) {
// The value of the sub element of the max layer is greater than the current lower bound, and the lower bound is updated
if (val > alpha) {
alpha = val;
}
// If the lower bound of max layer is greater than or equal to the upper bound, it will directly return to the lower bound (return the larger one)
if (alpha >= beta) {
node.value = 'A' + alpha;
return alpha;
}
} else {
// The upper bound is updated when the value of the min layer sub element is less than the value of the current upper bound
if (val < beta) {
beta = val;
}
// If the lower bound of min layer is greater than or equal to the upper bound, return to the upper bound directly (return the smaller one)
if (alpha >= beta) {
node.value = 'B' + beta;
return beta;
}
}
}
// Returns the extreme value of the current layer node for pruning the parent element (not alpha or beta)
node.value = player === 1 ? Math.max(...map) : Math.min(...map);
}
return node.value;
}
function main(tree) {
const res = minimax(1, tree);
//const res = alphaBeta(1, tree, Number.MIN_SAFE_INTEGER, Number.MAX_SAFE_INTEGER);
console.log(countMinimax);
//console.log(countAlphaBeta);
}
// 11 8
const tree1 = {
value: null,
children: [
{
value: null,
children: [
{
value: 7,
children: []
},
{
value: 3,
children: []
}
]
},
{
value: null,
children: [
{
value: 15,
children: []
}
]
},
{
value: null,
children: [
{
value: 1,
children: []
},
{
value: 12,
children: []
},
{
value: 20,
children: []
},
{
value: 22,
children: []
}
]
},
]
}
Firstly, two global variables countMinimax and countAlphaBeta are defined to record the minimax search algorithm and α-β The traversal times of pruning algorithm, and α-β The value value of the node reset where the pruning algorithm prunes makes the pruning more clear at a glance.
Again, use minimax and alphaBeta to operate Tree1 respectively, and get 11 and 8 results respectively. As expected, it traverses three times less, that is, three leaf nodes are subtracted.
More cases
Do you think the cases are not effective? Next, I have prepared more cases to compare the optimization effects of the two algorithms. You can also use your own cases to try. (the result of comparison is written directly on the notes)
// 13 11
const tree2 = {
value: null,
children: [
{
value: null,
children: [
{
value: 3,
children: []
},
{
value: 12,
children: []
},
{
value: 8,
children: []
}
]
},
{
value: null,
children: [
{
value: 2,
children: []
},
{
value: 100,
children: []
},
{
value: 8,
children: []
}
]
},
{
value: null,
children: [
{
value: 14,
children: []
},
{
value: 5,
children: []
},
{
value: 2,
children: []
}
]
}
]
}
// 22 22
const tree3 = {
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: 10,
children: [],
},
{
value: 20,
children: [],
}
]
},
{
value: null,
children: [
{
value: 5,
children: [],
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: -10,
children: []
}
]
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: 7,
children: [],
},
{
value: 5,
children: [],
}
]
},
{
value: null,
children: [
{
value: -8,
children: [],
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: -7,
children: [],
},
{
value: -5,
children: [],
}
]
}
]
}
]
}
]
}
// 26 17
const tree4 = {
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: 3,
children: []
},
{
value: 17,
children: []
}
]
},
{
value: null,
children: [
{
value: 2,
children: []
},
{
value: 12,
children: []
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: 15,
children: []
}
]
},
{
value: null,
children: [
{
value: 25,
children: []
},
{
value: 0,
children: []
}
]
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: 2,
children: []
},
{
value: 5,
children: []
}
]
},
{
value: null,
children: [
{
value: 3,
children: []
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: 2,
children: []
},
{
value: 14,
children: []
}
]
}
]
}
]
}
]
}
// 33 25
const tree5 = {
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: 5,
children: []
},
{
value: 6,
children: []
}
]
},
{
value: null,
children: [
{
value: 7,
children: []
},
{
value: 4,
children: []
},
{
value: 5,
children: []
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: 3,
children: []
}
]
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: 6,
children: []
}
]
},
{
value: null,
children: [
{
value: 6,
children: []
},
{
value: 9,
children: []
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: 7,
children: []
}
]
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: null,
children: [
{
value: 5,
children: []
}
]
}
]
},
{
value: null,
children: [
{
value: null,
children: [
{
value: 9,
children: []
},
{
value: 8,
children: []
}
]
},
{
value: null,
children: [
{
value: 6,
children: []
}
]
}
]
}
]
}
]
}
epilogue
So far, I believe everyone should be able to master the minimax search algorithm and α-β For pruning algorithm, the language used in this article is javascript, which is mainly used to describe specific examples, which will be more convenient. With these two algorithms as the cornerstone, there is hope for the ai Road of Chinese chess and Gobang.
Finally, if you have any questions about this article, please leave a message in the comment area or send me a private letter, and I will actively reply. I hope the content of this article can solve your doubts. See you in the next issue!