Problem description

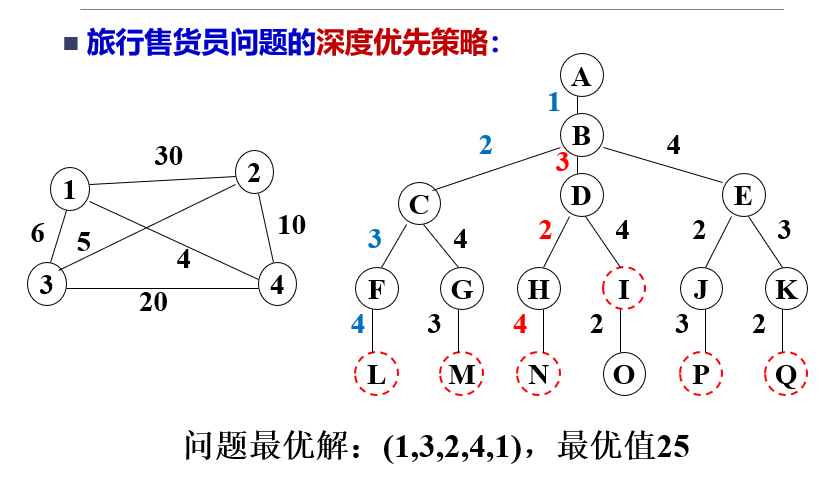
• A salesperson wants to sell goods in four cities. The distance between cities is known, as shown in the right figure.
  

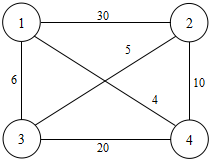
• How should he choose a route starting from city 1, passing through each city and finally returning to city 1, so as to minimize the total travel distance?

Train of thought analysis

Determine the solution space of the problem and express the problem first

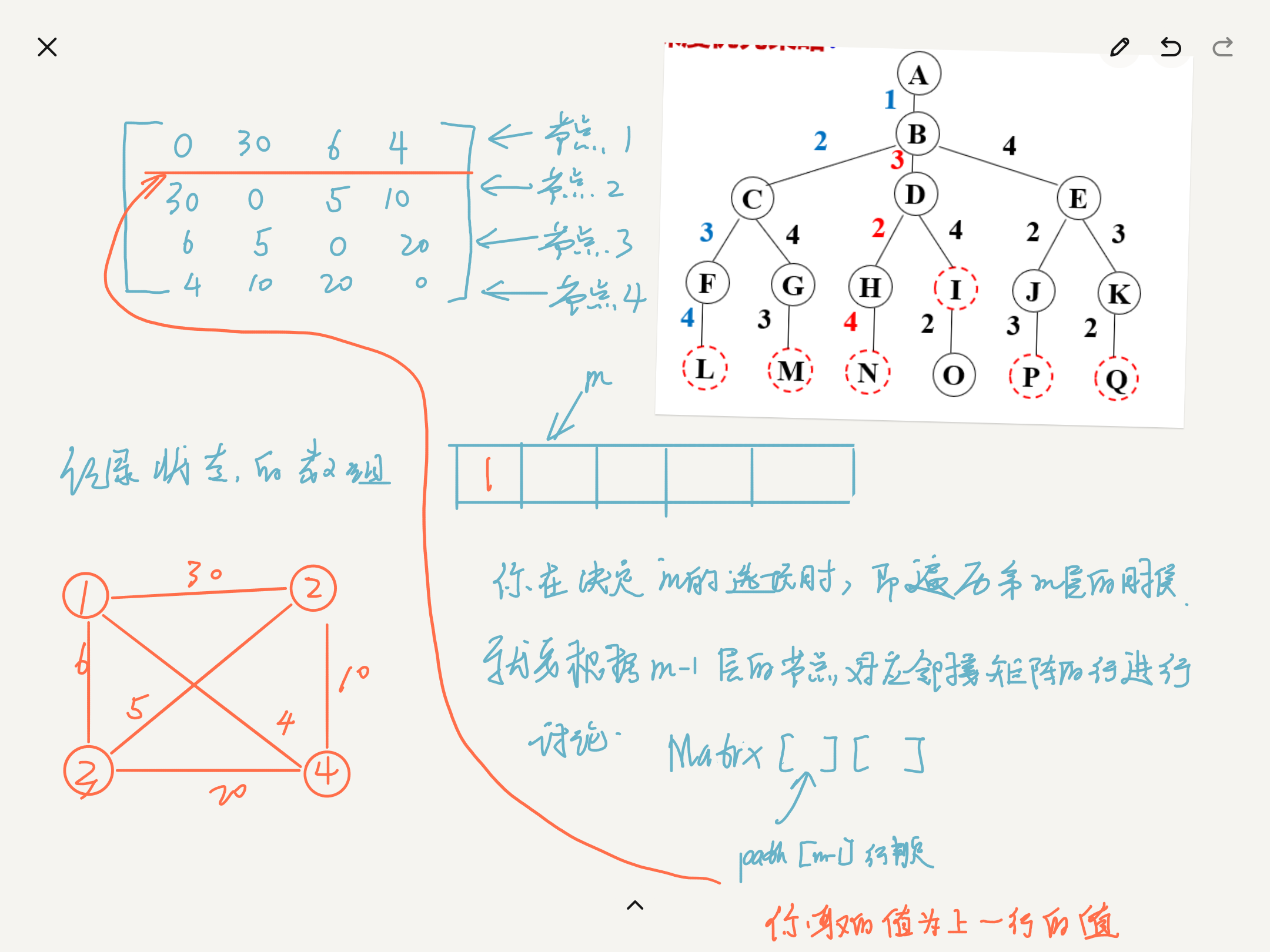
• First of all, you must save the input data. For the diagram, use the two-dimensional matrix here! Then the traversal starts from the adjacency matrix!

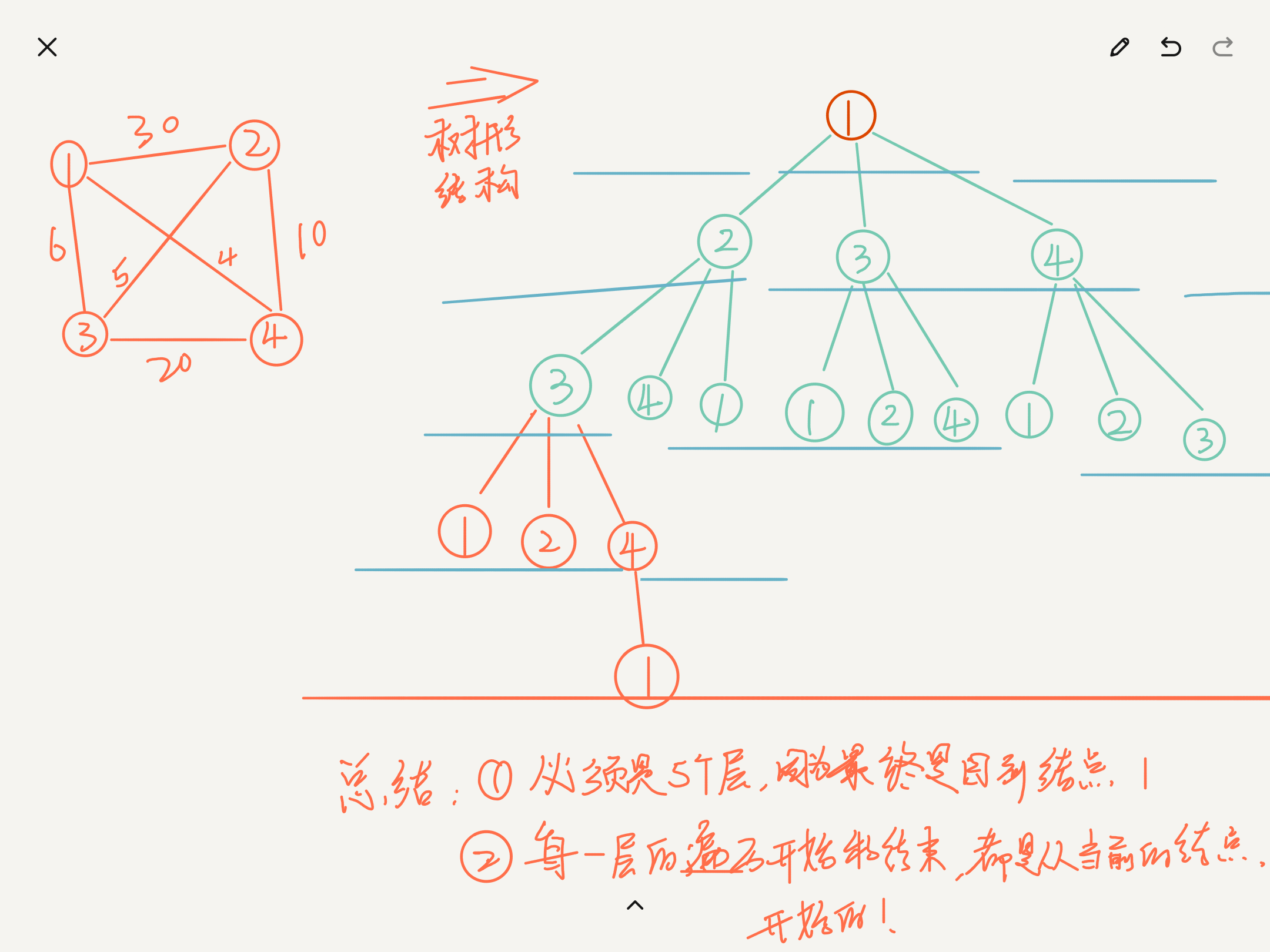
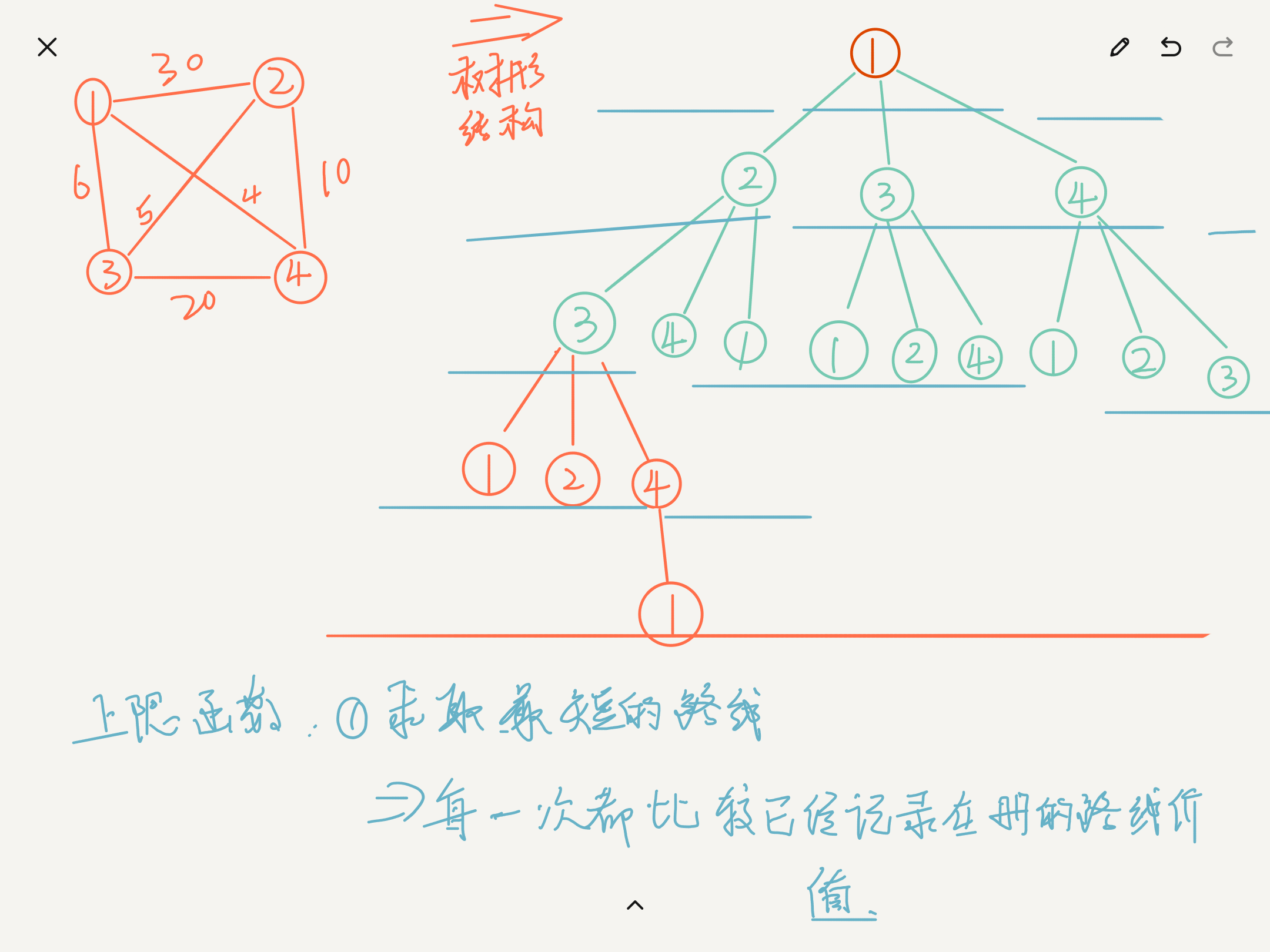
• When we use the tree structure to traverse the graph, it is easy to find that the repeated points do not need to be traversed, and only the first point needs to be traversed repeatedly!
  
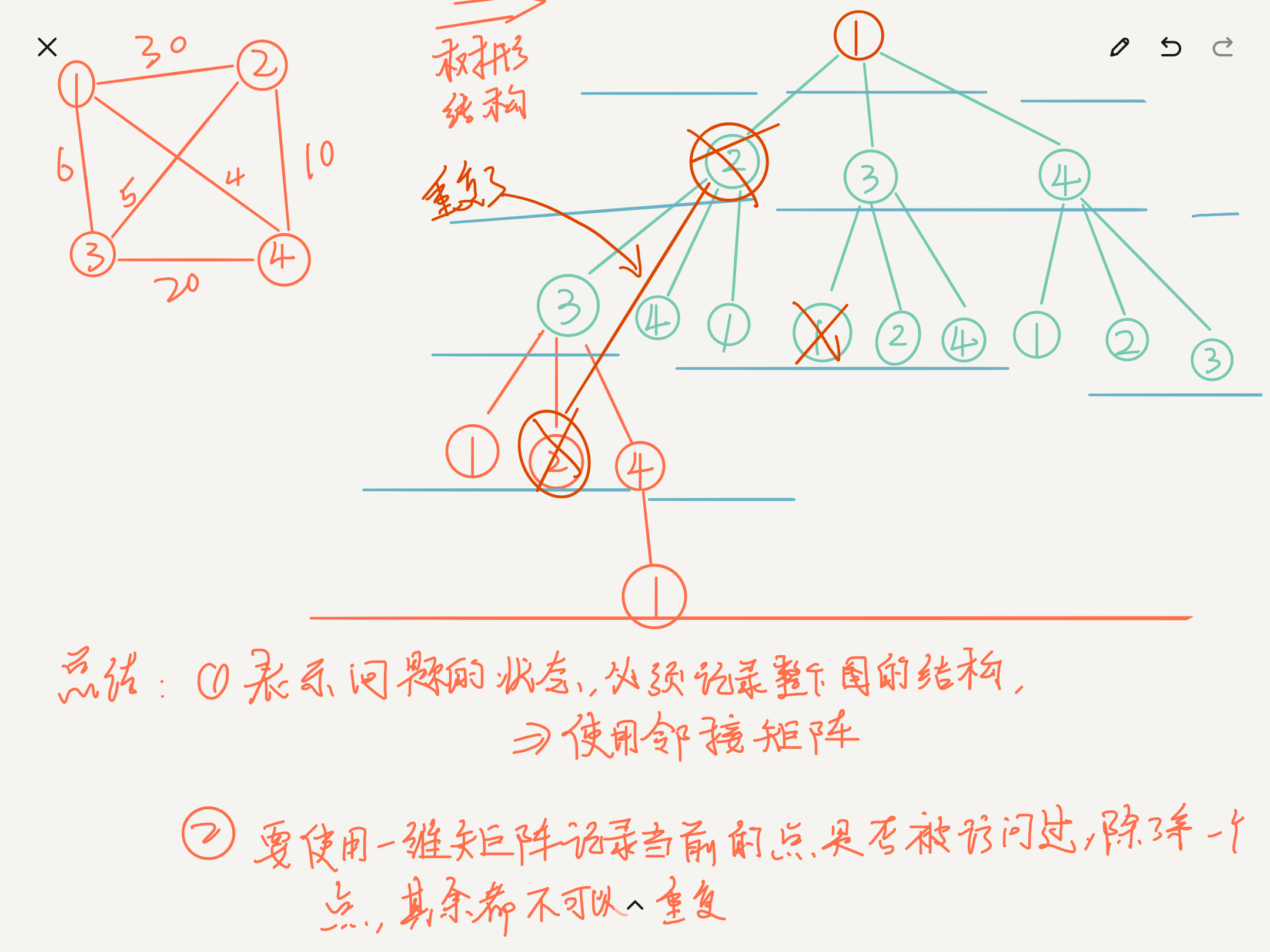
• Therefore, in general, two structures are needed:
  • Adjacency matrix to save the corresponding graph structure
  • One dimensional matrix to record whether each point is accessed.

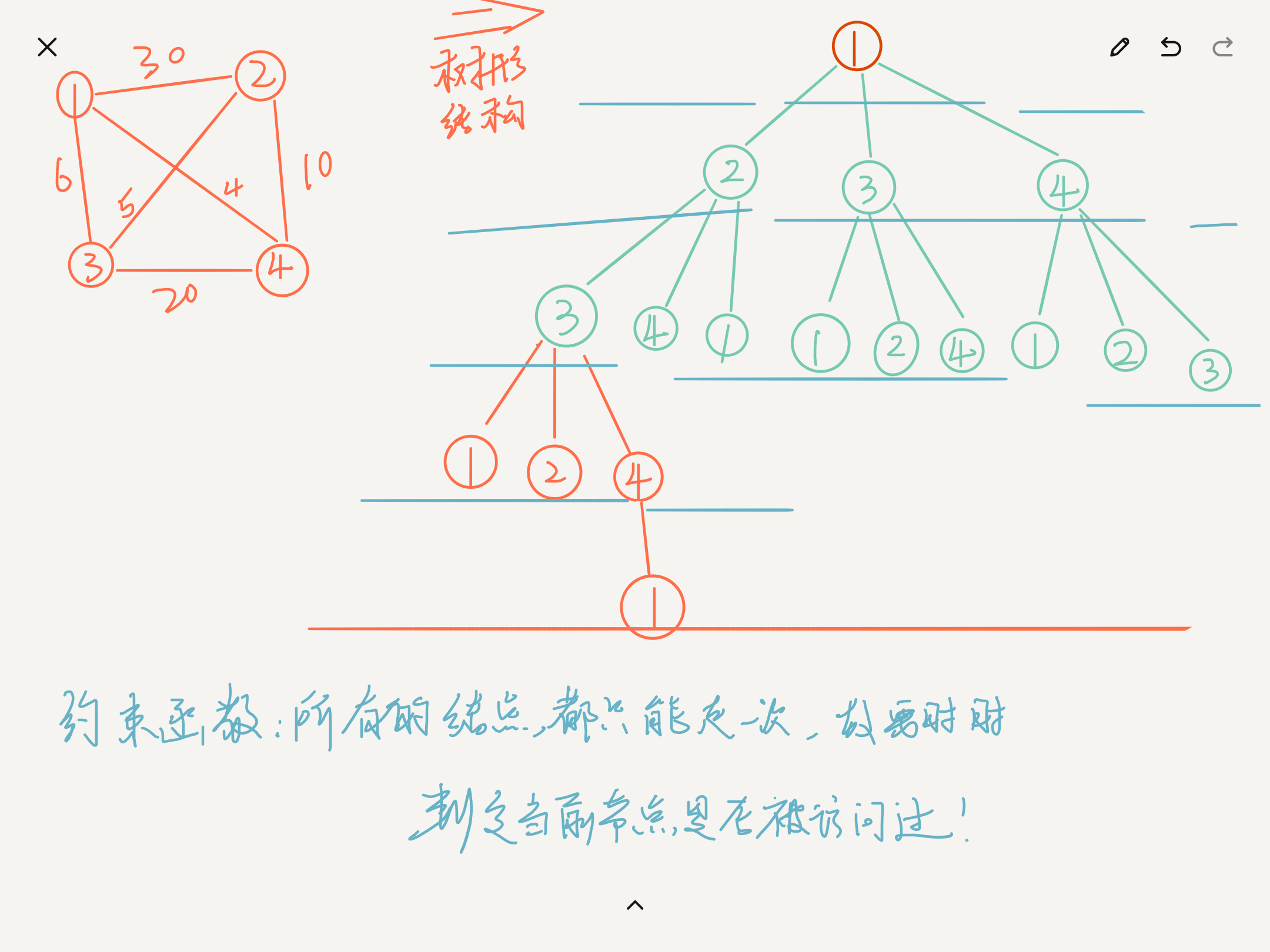
According to the requirements of the topic, determine the constraint function and upper bound function

• Constraint function: records all the accessed nodes. It is necessary to determine whether the current state is the accessed node!
  

• Upper limit function: determines whether the value of the current status has exceeded the value of the corresponding current completion!

Implementation code and analysis

Using program language representation

Definition of constraint function and upper bound function

//Save the currently known shortest path. Here, first define a maximum value. Once it is smaller than this value, it will be replaced with a smaller value
int minPath = 99;
//Save the path corresponding to the current state. There are four nodes in total, and you only need to walk four times in total
int path[4];

/*
	Description: the constraint function and upper bound function of travel sales problem ensure that the path is not repeated and the value of the path is the smallest
	Parameter: m indicates the state of the current problem, which is also the number of layers recursively, and records the location node of M choices
		 pathValue: Indicates the value of the path corresponding to the current state
	Return: true: indicates that the current node meets the corresponding conditions
		  false: Indicates that the current node does not meet the corresponding conditions
	Principle: traverse the existing array to see if it will be repeated
		 Compare the saved maximum value for judgment

*/
bool constrainAndBound(int m,int pathValue){

	//Constraint function to check whether the current decision conforms to the status
	for (int i = 0; i < m; ++i)
	{
		if (path[m] == path[i])
		{
			return false;
		}
	}

	//The upper bound function determines whether the current path value is the shortest
	
	//If you do not reach the target path, it is longer than the original path. You can exit directly
	if (m < 3)
	{
		pathValue > minPath;
		return false;
	}
	return true;
}

Retrospective algorithm review

• Define the solution space of the problem and all cases of the problem, including the optimal solution.
• Determine the solution space structure that is easy to search:
  • Subset tree
  • Permutation tree
• Determine the constraint function or bound function
• Depth traversal search solution space from root node

Implementation source code

• This problem is a little different, that is, the default is to start from the first node, specify the initial starting point, and formulate a complete cycle. There are five nodes, so the termination condition of traversal should be at the fifth layer.

//The following is the code of travel sales problem

//Save the currently known shortest path. Here, first define a maximum value. Once it is smaller than this value, it will be replaced with a smaller value
int minPath = 99;
//Save the path corresponding to the current state. There are four nodes in total, and you only need to walk four times in total
int path[5] = { 0 };
//Define a number of points
int placeNum = 4;
/*
	Description: the constraint function and upper bound function of travel sales problem ensure that the path is not repeated and the value of the path is the smallest
	Parameter: m indicates the state of the current problem, which is also the number of layers recursively, and records the location node of M choices
		 pathValue: Indicates the value of the path corresponding to the current state
	Return: true: indicates that the current node meets the corresponding conditions
		  false: Indicates that the current node does not meet the corresponding conditions
	Principle: traverse the existing array to see if it will be repeated
		 Compare the saved maximum value for judgment

*/
bool constrainAndBound(int m, int pathValue) {

	//Constraint function to check whether the current decision conforms to the status
	
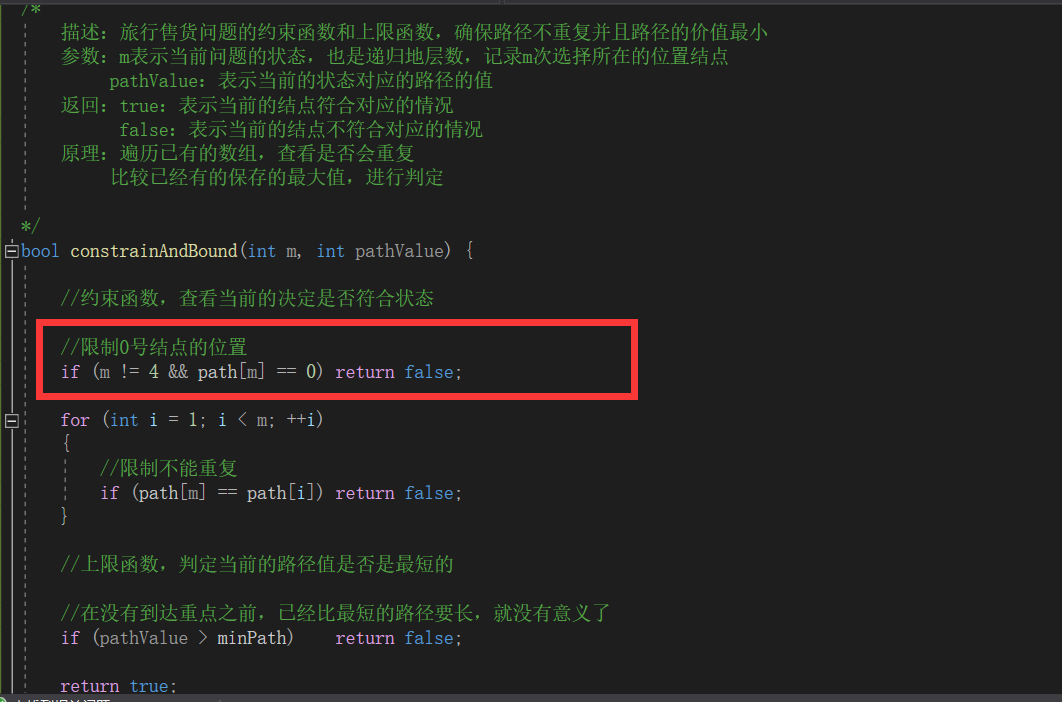
	//Limit the position of node 0
	if (m != 4 && path[m] == 0)	return false;

	for (int i = 1; i < m; ++i)
	{
		//Restrictions cannot be repeated
		if (path[m] == path[i])	return false;
	}

	//The upper bound function determines whether the current path value is the shortest

	//Before reaching the key point, it is longer than the shortest path, so it is meaningless
	if (pathValue > minPath)	return false;

	return true;
}

/*
	 Description: specific implementation of travel sales problem
	 Parameter: m indicates the depth of corresponding recursion
		  matrix A two-dimensional matrix that represents the shape of the corresponding matrix
		  pathValue Indicates the current path length
	 Return: no return value, recursive call
	 Principle: in the process of recursion, generate a tree and traverse the corresponding tree
*/
void SellPath(int m, int Matrix[4][4], int pathValue) {

	//The fourth goal is to reach the end of recursion first
	if (m == 5)
	{
		//When the bottom line is reached, directly compare the corresponding length
		if (pathValue < minPath)	minPath = pathValue;
		//Cout < < the shortest path is: < < minpath < < endl;
	}
	else {
		//If it is not satisfied, it will be traversed recursively, traversing the adjacent points of each location
		for (int i = 0; i < placeNum; ++i)
		{
			//If you traverse to the current state, you should traverse to the node corresponding to the current state
			//Locate the corresponding row in the two-dimensional matrix and traverse to find the node of the current target.
			if (Matrix[path[m - 1]][i] != 0)
			{
				//Accumulate the distance
				pathValue += Matrix[path[m - 1]][i];
				//Select status to determine whether the current status is legal
				path[m] = i;
				int temp = path[m];

				//Constraint conditions for judgment
				if (constrainAndBound(m, pathValue))
				{
					//If the recursion condition is met, recursion will be carried out, and recursion will be carried out in the next direction
					SellPath(m + 1, Matrix, pathValue);
				}
				//If the conditions are not met, the current path is subtracted
				pathValue -= Matrix[path[m-1]][i];


			}
		}
	}
}

int main(){
cout << "Display of tourism sales problems" << endl;
			cout << "There are four nodes in total, namely 1, 2, 3 and 4" << endl;
			cout << "There are 6 sides in total, which are 4, 5, 6, 10, 20 and 30 from low to high" << endl;
			//Initialize adjacency matrix
			int nodeNum = 4;
			int Matrix[4][4];
			int pathValue = 0;
			for (int i = 0; i < nodeNum; ++i)
			{
				for (int j = 0; j < nodeNum; ++j)
				{
					Matrix[i][j] = 0;
				}
			}
			Matrix[0][1] = 30;
			Matrix[0][2] = 6;
			Matrix[0][3] = 4;
			Matrix[1][0] = 30;
			Matrix[1][2] = 5;
			Matrix[1][3] = 10;
			Matrix[2][0] = 6;
			Matrix[2][1] = 5;
			Matrix[2][3] = 20;
			Matrix[3][0] = 4;
			Matrix[3][1] = 10;
			Matrix[3][2] = 20;
			cout << "The output matrix is as follows:" << endl;

			for (int i = 0; i < 4; ++i)
			{
				for (int j = 0; j < 4; ++j)
				{
					cout << Matrix[i][j] << "    ";
				}
				cout << endl;
			}

			SellPath(1, Matrix, pathValue);
			cout << "The final result is:" << minPath << endl;
			cout << endl;
			return 0;
}

Problems arising

When traversing, it jumps horizontally between node 1 and node 2 once, so that the final target node can not be found at last

• At the beginning, the first node is node 0 by default, and the last node is node 0 by default. Therefore, it is necessary to add corresponding judgment conditions to the constraint function to limit the location and selection of node 0!

Although there are four nodes here, you have to go through five nodes, starting from 1 and finally returning to 1!

• Therefore, the array recording the recursive state is a one-dimensional array with a length of 5, but the traversal starts from the second node, and the first node is 0 by default!

Two things are mainly used, one-dimensional matrix to save recursive state and two-dimensional matrix to save array information

• Note: the relationship between the above two is different by one state. The recursion option of m state is determined by the recursion option of m-1 state
  

Analysis and summary

• This question has been entangled for a long time, thought a lot, and found many different places! The key is that this problem requires a deep understanding of the problem-solving process and the backtracking process! Because he has many differences, many variants! You should set different conditions to judge according to the situation!
• This question really makes me gain a lot, but my code is not very good-looking, at least in my opinion, it is messy! And the quality is not high, it should be modified! However, I have invested a lot of time in thinking about the solution, so I don't have time to modify it!
• Please buckle if you have something to do! 651378276! We can learn and make progress together!