Part 27 shift inversion iteration to find the nearest eigenvalue and eigenvector

Shift inverse iteration

An eigenvalue method to realize vector iterative convergence more directly than the "maximum" eigenvalue method is Shift vector iteration method Rewrite to the following form

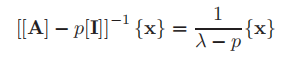
Where p is a scalar "shift" value, [I] is the identity matrix, λ Is the eigenvalue of [a]. as Fundamentals of eigenvalue programming As shown in, the eigenvector of [[A] − p[I] − 1 is the same as that of [A], but it can be proved that the eigenvalue of [[A] − p[I] − 1 is 1/( λ −p). Therefore, the maximum eigenvalue of [[A] − p[I]] − 1 causes the eigenvalue of [A] to be closest to P. Therefore, if the maximum eigenvalue of [[A] − p[I]] − 1 is μ， Then the eigenvalue of [A] closest to p is

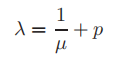
For small matrices, only the inverse of [[A] − p[I]] is required, and the inverse iteration is used to solve the equation, which is exactly the same as the algorithm used in solving linear equations. However, for larger matrices, the factorization method in linear equations is more applicable, especially when dealing with multiple right vector values and A constant coefficient matrix. Therefore, in the normal shift iteration method, it must be calculated in each iteration

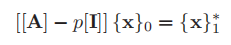
In the inverse iteration, we need to calculate

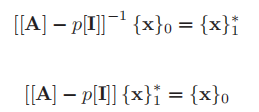
By using the subroutine lufac, factorization [A] − p[I] is obtained

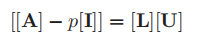
have to

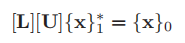
If you let me

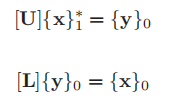
The solution process is divided into two steps, first solve {y}0, and then solve {x}1. This method is exactly the same as the previous iteration and post iteration, so you need to use the previous subroutines, subfor and subbac. For details, please see LDLT decomposition Gaussian elimination
By replacing p in the system, all eigenvalues can be obtained.
Calculation example
Using the shift inversion method, find the eigenvalue of the following matrix closest to 2

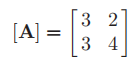
For this small problem, it can be calculated directly by hand

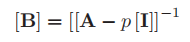
When p takes 2 in this example

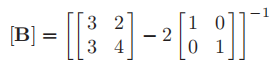
therefore

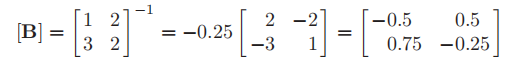
Let {x} 0 = {1} T and {x} * k be the values before {x}k orthogonalization.
First iteration (k=1)

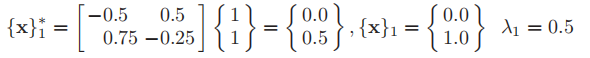
Second iteration (k=2)

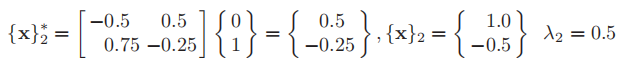
The third iteration (k=3)


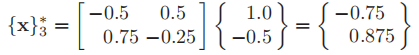
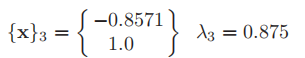
The fourth iteration (k=4)

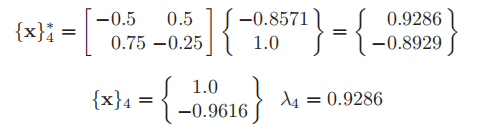
After many iterations

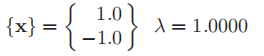
The procedure is as follows:
There is a main program and four subroutines, which are respectively the subroutine checkit for checking convergence, the subroutine lufac for factorization, the subroutine subfor of the former iteration method and the subroutine subbac of the latter iteration method.

#Shift and inverse vector iteration of eigenvalues and eigenvectors
import numpy as np
import B
n=3;tol=1.0e-5;limit=100;shift=20.0
lower=np.zeros((n,n))
upper=np.zeros((n,n))
a=np.array([[10,5,6],[5,20,4],[6,4,30]],dtype=np.float)
x1=np.zeros((n,1))
x=np.ones((3,1),dtype=np.float)
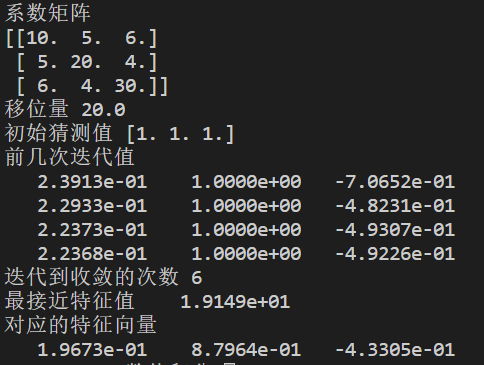
print('coefficient matrix')
print(a[:])
print('Displacement',shift)
print('Initial guess value',x[:,0])
for i in range(1,n+1):
    a[i-1,i-1]=a[i-1,i-1]-shift
B.lufac(a,lower,upper)
print('Previous iteration values')
x1[:,0]=x[:,0]
iters=0
while(True):
    iters=iters+1
    B.subfor(lower,x1)
    B.subbac(upper,x1)
    big=0.0
    for i in range(1,n+1):
        if abs(x1[i-1,0])>abs(big):
            big=x1[i-1,0]
    x1[:,0]=x1[:,0]/big
    if  B.checkit(x1,x,tol)==True or iters==limit:
        break
    x[:,0]=x1[:,0]
    if iters<5:
        for i in range(1,n+1):
            print("{:13.4e}".format(x[i-1,0]),end=" ")
        print(end="\n")
l2=np.linalg.norm(x1)
x1[:,0]=x1[:,0]/l2
print('Number of iterations to convergence',iters)
print('Closest eigenvalue',"{:13.4e}".format(1.0/big+shift))
print('Corresponding eigenvector')
for i in range(1,n+1):
    print("{:13.4e}".format(x1[i-1,0]),end=" ")

checkit	

def checkit(loads,oldlds,tol):
#Check the convergence of multiple unknowns
  neq=loads.shape[0]
  big=0.0
  converged=True
  for i in range(1,neq+1):
    if abs(loads[i-1,0])>big:
      big=abs(loads[i-1,0])
  for i in range(1,neq+1):
    if abs(loads[i-1,0]-oldlds[i-1,0])/big>tol:
      converged=False
  checkit=converged
  return  checkit

lufac

ef lufac(a,lower,upper):
  n=a.shape[0]
  upper[0,:]=a[0,:]
  for i in range(1,n+1):
    lower[i-1,i-1]=1.0
  for k in range(1,n):
    if abs(upper[k-1,k-1])>1.0e-10:
      for i in range(k+1,n+1):
#Lower triangular decomposition
        for j in range(1,i):
          total=0
          for l in range(1,j):
            total=total-lower[i-1,l-1]*upper[l-1,j-1]
          lower[i-1,j-1]=(a[i-1,j-1]+total)/upper[j-1,j-1]
#Upper triangular decomposition
        for j in range(1,n+1):
          total=0
          for l in range(1,i):
            total=total-lower[i-1,l-1]*upper[l-1,j-1]
          upper[i-1,j-1]=a[i-1,j-1]+total
    else:
      print('There is a 0 vector in the second',k,'that 's ok')
      break

subfor

def subfor(a,b):
#Forward iteration method for a lower triangle
  n=a.shape[0]
  for i in range(1,n+1):
    total=b[i-1]
    if i>1:
      for j in range(1,i):
        total=total-a[i-1,j-1]*b[j-1]
    b[i-1]=total/a[i-1,i-1]

subbac

def subbac(a,b):
#A backward iteration method for a lower triangle
  n=a.shape[0]
  for i in range(n,0,-1):
    total=b[i-1]
    if i<n:
      for j in range(i+1,n+1):
        total=total-a[i-1,j-1]*b[j-1]
    b[i-1]=total/a[i-1,i-1]

Output terminal