Longest double palindrome string

Title Link: ybt gold navigation 2-1-3 / luogu P4555

General idea of the topic

Give you a string and ask you to find the longest substring so that it is composed of two palindrome strings.

thinking

First, let's see the palindrome string. Let's run a Manacher first.

Then we'll think about what to do.
First, let's talk about the method of segment tree, and then talk about the better DP method.

Segment tree

Then you will think that you need to find two points as the center of two palindrome strings, and then their longest palindrome string can be connected or intersected.
Because in this way, you can spell the string required by a topic, and its length is the direct distance between the two points multiplied by two.

Then you can enumerate the points, and then how many right endpoints of the points in front of it are behind your left endpoint. Find the point with the smallest number among the points that meet the requirements.
Then you naturally think of using segment trees.

That's OK, but because you deal with the string at the beginning, the final answer has to be divided by two, which offsets the multiplication of two calculated previously, and is directly the length between the two points.

DP

The above method is nlogn. Can you O(n)?

In fact, you can start.
Since it is divided into two palindromes, let's consider where the segmentation point is. Then extend the left and right sides as far as possible.

Then we are actually asking for two arrays.
l l i ll_i lli ， denotes i i i is the longest length of the palindrome string at the left end of the palindrome string, r r i rr_i rri ， denotes i i i is the longest length of the palindrome string at the right end of the palindrome string.

Then consider what you want.
It cannot be calculated only by the length obtained by Manacher, because it is only the longest centered on it, and the second longest or others may become the best in other positions.
And you can't enumerate the length one by one, which will timeout.

Then you can think about it.
with l l i ll_i For example, you can enumerate from right to left # \# #(Manacher separator), and then l l i = max ⁡ { l l i , l l i + 2 − 2 } ll_i=\max\{ll_i,ll_{i+2}-2\} lli​=max{lli​,lli+2​−2}

What does that mean?
In fact, it means that it can make you come farther, and then reduce a length.

This is the picture:

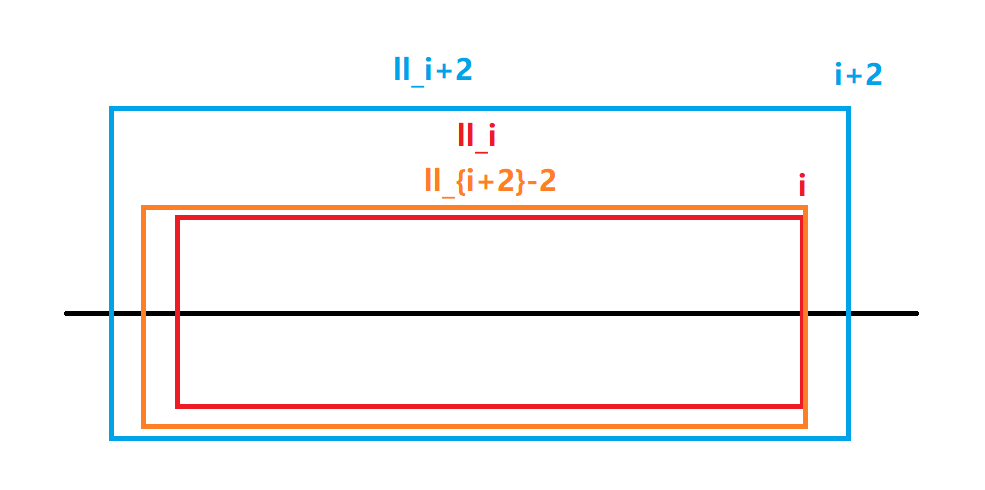
then r r i rr_i rri # did the same and got these two.

Then we enumerate i i As endpoint i, l l i + r r i ll_i+rr_i The maximum value of lli + rri +.

But it must be composed of two palindrome strings, so you must ensure that l l i > 0 ll_i>0 lli > 0 and r r i > 0 rr_i>0 rri > 0 can be used to compare the maximum value.

Code (segment tree + Manacher)

#include<cstdio>
#include<cstring>
#include<iostream>
#define INF 2147483647

using namespace std;

char s[300001], c[300001];
int n, dis[300001], nn, ans;
int fr[300001], tr[300001];
int tree[1600001], maxdis;

void up(int now) {
	tree[now] = min(tree[now << 1], tree[now << 1 | 1]);
}

void build(int now, int l, int r) {//initialization
	tree[now] = INF;
	
	if (l == r) {
		return ;
	}
	
	int mid = (l + r) >> 1;
	build(now << 1, l, mid);
	build(now << 1 | 1, mid + 1, r);
	
	up(now);
}

int get_min(int now, int l, int r, int L, int R) {//Find the minimum right boundary satisfied
	if (l > r) return 0;
	if (l >= L && r <= R) {
		return tree[now];
	}
	
	int mid = (l + r) >> 1, re = INF;
	if (mid >= L) re = min(re, get_min(now << 1, l, mid, L, R));
	if (mid < R) re = min(re, get_min(now << 1 | 1, mid + 1, r, L, R));
	return re;
}

void insert(int now, int l, int r, int pl, int num) {//Insert right border
	if (l == r) {
		tree[now] = min(tree[now], num);
		return ;
	}
	
	int mid = (l + r) >> 1;
	if (pl <= mid) insert(now << 1, l, mid, pl, num);
		else insert(now << 1 | 1, mid + 1, r, pl, num);
	
	up(now);
}

void manacher() {//Run Manacher, the same below
	int r = -1, mid = -1;
	for (int i = 1; i <= nn; i++) {
		if (i > r) dis[i] = 1;
			else dis[i] = min(dis[2 * mid - i], r - i);
		while (i - dis[i] >= 1 && i + dis[i] <= nn && c[i + dis[i]] == c[i - dis[i]])
			dis[i]++;
		if (i + dis[i] > r) {
			r = i + dis[i] - 1;
			mid = i;
		}
		
		ans = max(ans, i - get_min(1, 1, nn, i - dis[i] + 1, nn));
		insert(1, 1, nn, i + dis[i], i);
		maxdis = max(maxdis, dis[i]);
	}
}
int main() {
	scanf("%s", s + 1);
	n = strlen(s + 1);
	
	nn = 2 * n + 1;
	build(1, 1, nn);
	for (int i = 1; i <= nn; i++)
		if (i & 1) c[i] = '#';
			else c[i] = s[i / 2];
	
	manacher();
	
	if (maxdis - 1 == n && ans == n) printf("%d", n - 1);//It must be divided into two
		else printf("%d", ans);
	
	return 0;
}

Code (DP+Manacher)

#include<cstdio>
#include<cstring>
#include<iostream>

using namespace std;

char s[300001], c[300001];
int n, dis[300001], nn, ans;
int ll[300001], rr[300001];

void manacher() {
	int r = -1, mid = -1;
	for (int i = 1; i <= nn; i++) {
		if (i > r) dis[i] = 1;
			else dis[i] = min(dis[2 * mid - i], r - i);
		while (i - dis[i] >= 1 && i + dis[i] <= nn && c[i + dis[i]] == c[i - dis[i]])
			dis[i]++;
		if (i + dis[i] > r) {
			r = i + dis[i];
			mid = i;
		}
		
		ll[i + dis[i] - 1] = max(ll[i + dis[i] - 1], dis[i] - 1);//Record the left and right boundaries
		rr[i - dis[i] + 1] = max(rr[i - dis[i] + 1], dis[i] - 1);
	}
}

int main() {
	scanf("%s", s + 1);
	n = strlen(s + 1);
	
	nn = 2 * n + 1;
	for (int i = 1; i <= nn; i++)
		if (i & 1) c[i] = '#';
			else c[i] = s[i / 2];
	
	manacher();
	
	for (int i = 3; i <= nn; i += 2)//DP shows that all palindrome strings are leftmost and rightmost (the first one is the one with the longest center point of each)
		rr[i] = max(rr[i], rr[i - 2] - 2);
	for (int i = nn - 2; i >= 1; i -= 2)
		ll[i] = max(ll[i], ll[i + 2] - 2);
	
	for (int i = 3; i <= nn; i += 2)//Enumerate split points
		if (ll[i] && rr[i]) ans = max(ll[i] + rr[i], ans);
	
	printf("%d", ans);
	
	return 0;
}