1, Experimental purpose

Master the basic principle of DPCM codec system. Preliminarily master the experiment, program the DPCM encoder with C/C++/Python and other languages, and analyze its compression efficiency.

2, Main equipment

Personal computers with Windows and Visual Studio software installed

3, Experimental content

1. DPCM encoding and decoding principle

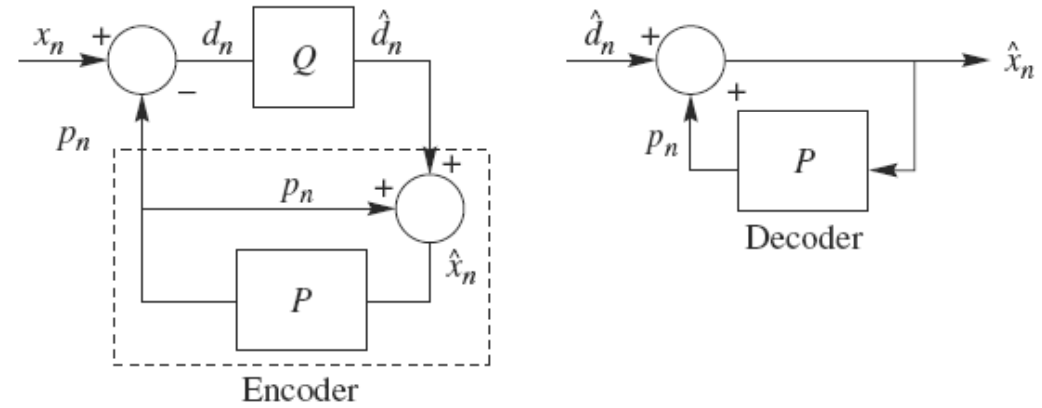
DPCM is the abbreviation of differential predictive coding modulation. It is a typical predictive coding system. In DPCM system, it should be noted that the input of predictor is the decoded sample. The reason why the original samples are not used for prediction is that the original samples cannot be obtained at the decoding end, and only the samples with errors can be obtained. Therefore, a decoder is actually embedded in the DPCM encoder, as shown in the dotted box in the encoder.

In a DPCM system, two factors need to be designed: predictor and quantizer. Ideally, the predictor and quantizer should be jointly optimized. In practice, a suboptimal design method is adopted: the optimal design of linear predictor and quantizer is carried out respectively.

2. Design of DPCM coding system

In this experiment, we use fixed predictor and uniform quantizer. The predictor adopts both left and upper prediction. The quantizer adopts 8-bit uniform quantization.
The goal of this experiment is to verify the coding efficiency of DPCM coding.

• Firstly, a 256 level gray image is read, the prediction error is calculated by using the prediction method set by ourselves, and the prediction error is uniformly quantized by 8 bits (basic requirements). The prediction error can also be quantized by 1-bit, 2-bit and 4-bit (improve the requirements).
• During the implementation of DPCM encoder, the prediction error image and reconstructed image can be output at the same time.
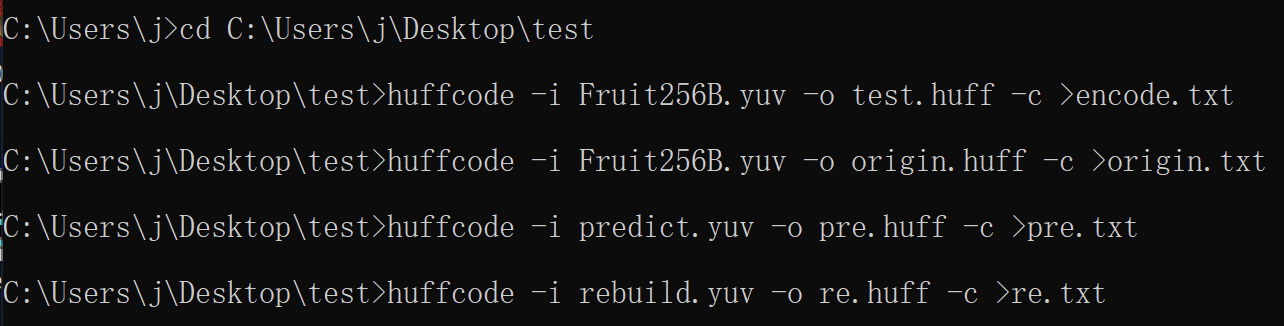
• Write the prediction error image into the file and input the file into Huffman encoder to obtain the output code stream, give the probability distribution diagram and calculate the compression ratio.
• Input the original image file into Huffman encoder, get the output code stream, give the probability distribution diagram and calculate the compression ratio.
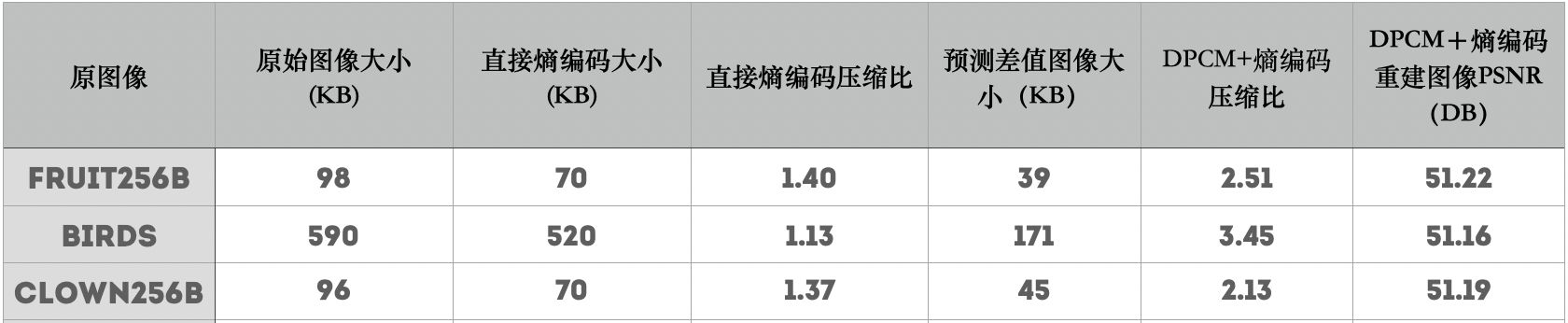
• Finally, the coding efficiency (compression ratio and image quality) between the two systems (DPCM + entropy coding and entropy coding only) is compared. The compression mass is calculated as PSNR.

3. PSNR and MSE

• PSNR is the abbreviation of "Peak Signal to Noise Ratio", that is, peak signal-to-noise ratio. It is an objective standard for evaluating images. It has limitations and is generally used in an engineering project between maximum signal and background noise. Unit: dB.
  
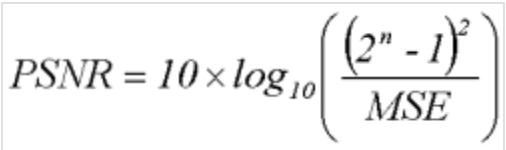
• MSE is the mean square error between the original image (voice) and the processed image (voice). n is the number of bits per sample value.

4. Some experimental codes

• main function part code

//DPCM
    //Operate only on the y-channel
    FILE  *predictPic = NULL, *rebuildPic = NULL;
	//Open forecast and rebuild file
    if ((predictPic = fopen(argv[3], "wb+")) == NULL)
    {
        printf("predict.yuv open fail!\n");
        exit(0);
    }
    if ((rebuildPic = fopen(argv[4], "wb+")) == NULL)
    {
        printf("rebuild.yuv open fail!\n");
        exit(0);
    }
    unsigned char *origin = NULL;
    unsigned char *pre_e = NULL;
    unsigned char *rebuild = NULL;
	//Open up the original image data buffer, predict the error image file data buffer, and reconstruct the image file buffer
    origin = (unsigned char *)malloc(width*height* sizeof(char));
    pre_e = (unsigned char *)malloc(width*height* sizeof(char));
    rebuild = (unsigned char *)malloc(width*height * sizeof(char));
	
	DPCM(yBuff, pre_e, rebuild,width,height);

    unsigned char *uv;
    uv = (unsigned char *)malloc(width*height/2* sizeof(char));
    for (int i = 0;i < width*height/2;i++)
    {
        uv[i] = 128;//There is no need to consider the UV channel, just consider the Y component, and set the UV channel to 128
    }

	//Calculate MSE and PSNR
	double MSE=0,PSNR=0;
	for (int i = 0; i <width*height ;i++)
	{
		MSE = MSE + pow ((yBuff[i] - rebuild[i]), 2.0);
	}
	MSE = MSE / (width*height);
	PSNR = 10 * log10((255 * 255) / MSE);
	printf("MSE is %lf\n", MSE);
	printf("PSNR is %lf\n", PSNR);

	//Write prediction and reconstruction files
    fwrite(pre_e, 1, width*height, predictPic);
    fwrite(uv, 1, (height * width) / 2, predictPic);

    fwrite(rebuild, 1, width*height, rebuildPic);
    fwrite(uBuff, 1, (height * width) / 4, rebuildPic);
    fwrite(vBuff, 1, (height * width) / 4, rebuildPic);


    //Freeing memory and closing files
    free(pre_e);
    free(rebuild);
	free(rgbBuf);
    free(yBuff);
    free(uBuff);
    free(vBuff);
    fclose(predictPic);
    fclose(rebuildPic);
    fclose(bmpFile);
    fclose(yuvFile);
	system("pause");

• DPCM function code

#include <stdio.h>
#include <stdlib.h>
#include <math.h>


int i = 8;	//Quantization of i bit

//quantizer 
unsigned char Q(int error)
{
	unsigned char pre_e;
	pre_e = error / pow (2.0, 9 - i);
	return pre_e;
}
//inverse quantizer 
unsigned char QT(unsigned char pre_e)
{
	unsigned char pre_eT;
	pre_eT = pre_e * pow (2.0, 9 - i);
	return pre_eT;
}

//DPCM
void DPCM(unsigned char *origin, unsigned char *pre_e, unsigned char *rebuild,int w,int h)
{
	int *error;
	error = (int *)calloc(w*h, sizeof(int));
	//int error[w*h] = { 0 };

	//Take the gray data in the original in turn, and judge whether the pixel is the first pixel in each line of the image
	for (int i = 0;i < w;i++)
	{
		for (int j = 0;j < h;j++)
		{
			//If yes, predict = 0 here, and the rebuild value is equal to the value in original
			rebuild[w*j] = origin[w*j];
			pre_e[w*j] = 0;
			//If not, pre here_ E gray value is the gray value of the original image minus the gray value of the previous pixel in the reconstructed image, and ibit quantization is performed
			if (i > 0)
			{
				error[i] = origin[w*j + i] - rebuild[w*j + i - 1];
				pre_e[w*j + i] = Q(error[i]);
				//Here, the rebuild gray value is pre_e add the rebuild value of the previous pixel after inverse quantization;
				QT(pre_e[w*j + i]);
				rebuild[w*j + i] = rebuild[w*j + i - 1] + QT(pre_e[w*j + i]);
			}
		}
	}
	for (int i = 0;i < w*h;i++)
	{
		pre_e[i] = pre_e[i] + 128;//Pre_ Add 128 to the gray value in e to make it all positive;
		if (pre_e[i] > 255)		pre_e[i] = 255;
	}
	for (int i = 0;i < w*h;i++)
	{
		if (rebuild[i] > 255)   rebuild[i] = 255;
		if (rebuild[i] < 0)		rebuild[i] = 0;
	}
}

4, Experimental results and analysis

• Use YUVviewer to view the original image, predicted difference image and reconstructed image

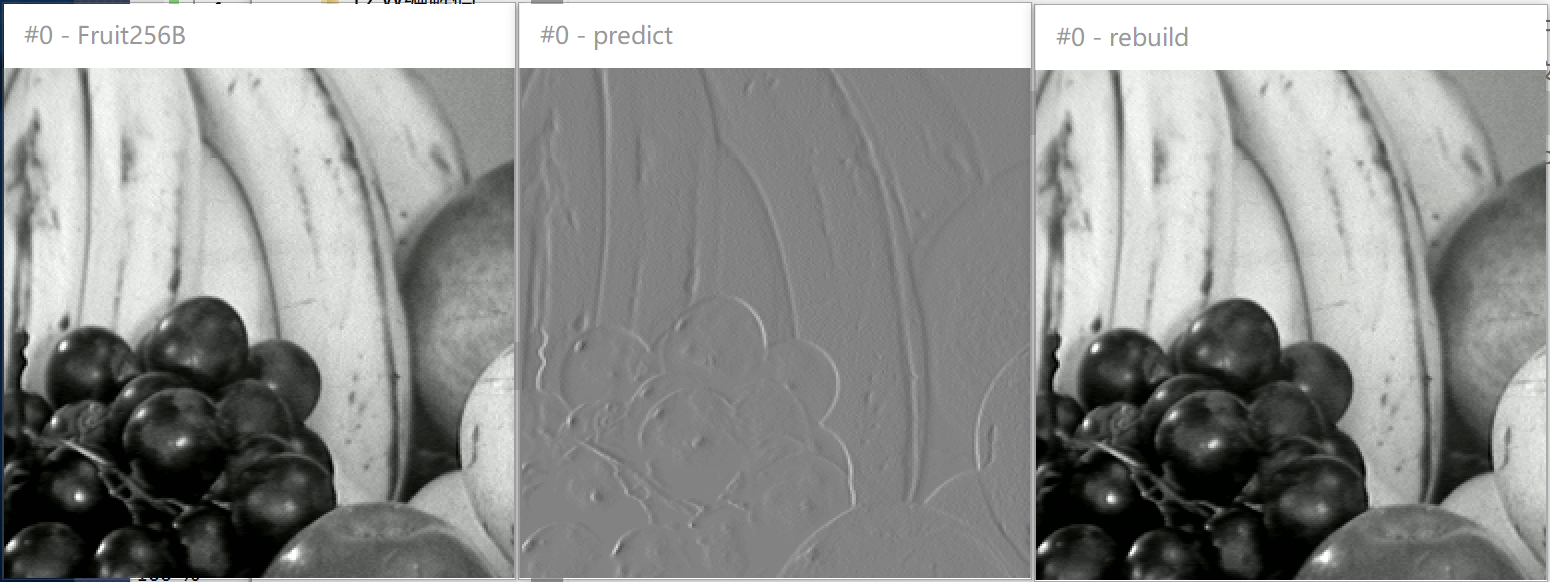
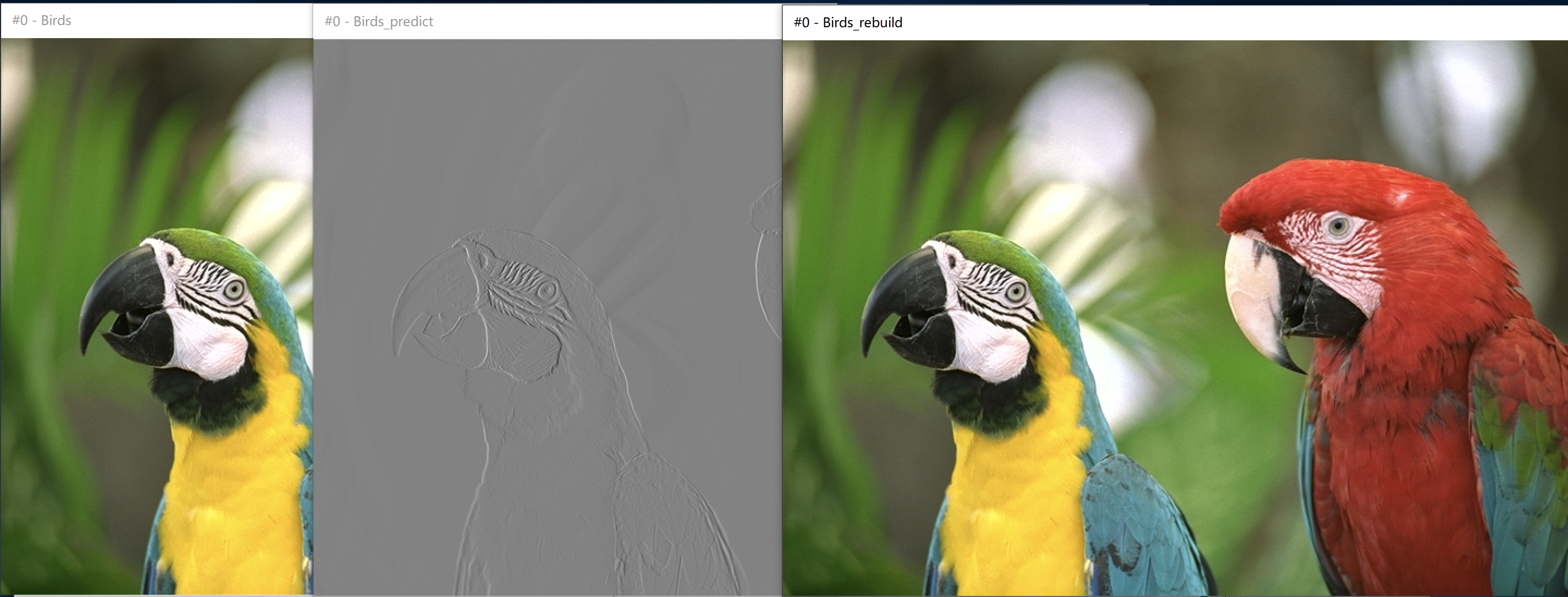
• The original image and prediction error image are compressed by huffman encoder, and the compression ratio is checked and compared
  

• Use the Number table to draw the probability distribution of the original image and the predicted image
  
  
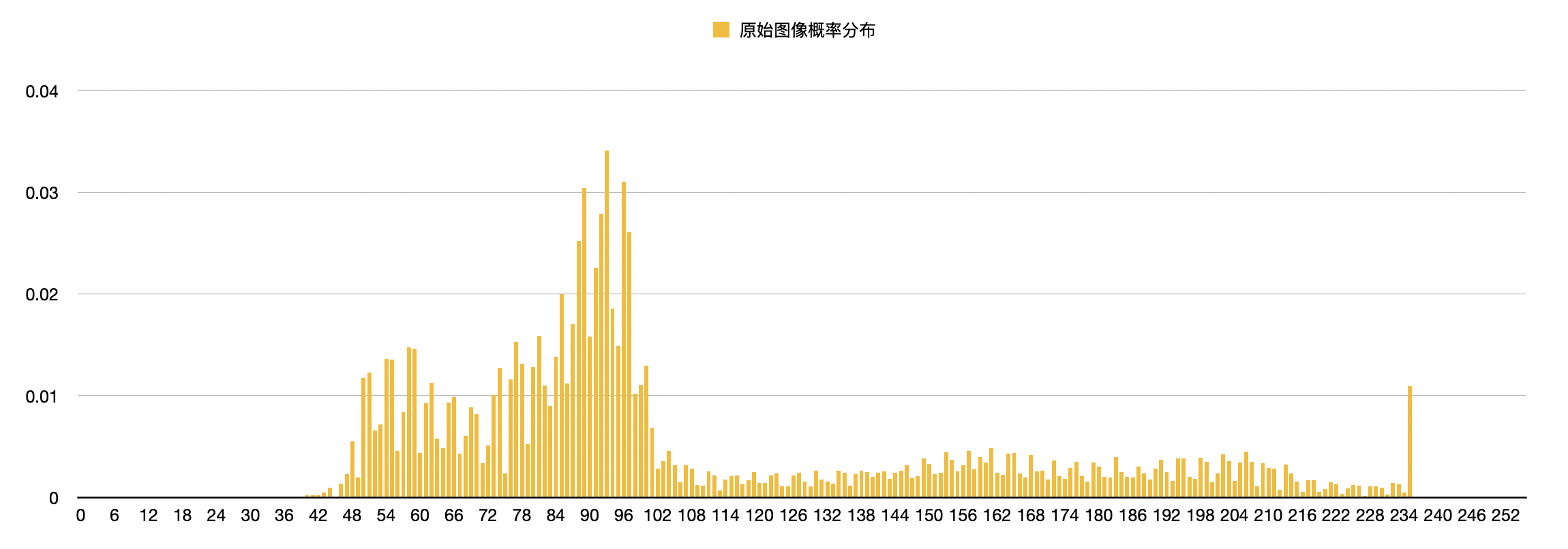
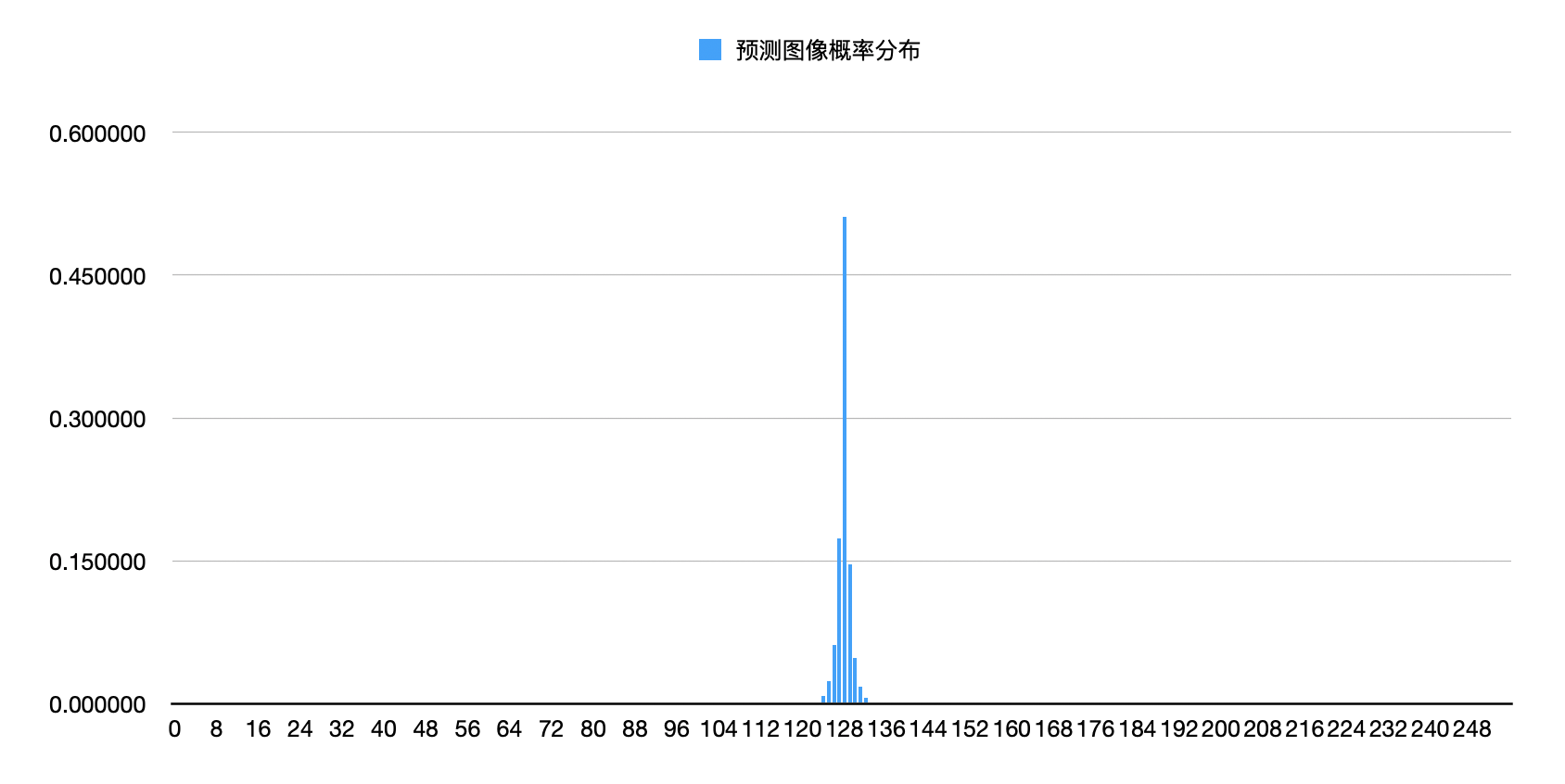
• Result analysis: it can be seen from the picture that the distribution of the original map is relatively uniform, while the probability distribution of the prediction error map is very concentrated, similar to Laplace distribution. In Huffman coding, there are few source symbols to be written, and most of them will be written in short code. This source compression method greatly reduces the amount of data, but the amount of information does not change. In other words, this coding method realizes energy concentration. The only error source may be the quantization and inverse quantization process of DPCM. From the calculated entropy and probability distribution map, it can be seen that the entropy of the original image is larger, and the image after distribution comparison is more uniform. When the distribution frequency tends to equal probability, the efficiency of Huffman coding is lower.