Catalogue of series articles
I Array type problem solving method 1: dichotomy
II Array type problem solving method 2: Double finger needle method
III Array type problem solving method 3: sliding window
IV Array type problem solving method 4: simulation
V The basic operation and classic topics of the linked list
Vi Classic title of hash table
VII Classic title of string
VIII KMP of string
IX Solution: double pointer
X Classic title of stack and queue
Xi top-K problem in stack and queue
XII The first, middle and last order traversal of binary tree
XIII Sequence traversal of binary tree and related topics
XIV Binary tree part of binary tree attributes related topics
XV Modification and construction of binary tree in binary tree chapter
XVI Properties of binary search tree
XVII The problem of common ancestor in binary tree discourse
Updating
preface
The question brushing route comes from: Code Capriccio
Inscription
701. Insert operation in binary search tree
Leetcode link
Given the root node root of the binary search tree (BST) and the value to be inserted into the tree, insert the value into the binary search tree. Returns the root node of the inserted binary search tree. Any value in the original binary tree is guaranteed to be different from that in the new binary tree. Note that there may be many effective insertion methods, as long as the tree remains a binary search tree after insertion. You can return any valid result.
Example 1:
Input: root = [4,2,7,1,3], val = 5
Output: [4,2,7,1,3,5]
Explanation: another tree that can meet the requirements of the topic is:
Example 2:
Input: root = [40,20,60,10,30,50,70], val = 25
Output: [40,20,60,10,30,50,70,null,null,25]
Example 3:
Input: root = [4,2,7,1,3, null, null, null, null, null], Val = 5
Output: [4,2,7,1,3,5]
Solution:
Traverse according to the rules of binary search tree, and insert the node when encountering an empty node
Method 1: recursion
Use the return value to complete the assignment operation between the newly added node and its parent node,
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) return new TreeNode(val);
// This layer uses root - > left or root - > right to connect it to the node returned by the next layer
// Possible of lower level return nodes:
// 1. When an empty node is encountered during downward recursion, the constructed val node can be returned
// 2. Return when backtracking up
if (val < root.val) root.left = insertIntoBST(root.left, val);
if (val > root.val) root.right = insertIntoBST(root.right, val);
return root;
}
}
Mode 2: iterative method
When traversing to null, add a new node and need to know the parent node, so use a node to save the parent node
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) return new TreeNode(val);
TreeNode cur = root;
TreeNode pre = root;
while (cur != null) {
// Save parent node
pre = cur;
// Find insertion location
if (val > cur.val) {
cur = cur.right;
} else if (val < cur.val) {
cur = cur.left;
}
}
// At this time, we don't know whether the insertion position is the left or right of the parent node. We need to judge
if (val < pre.val) {
pre.left = new TreeNode(val);
} else {
pre.right = new TreeNode(val);
}
return root;
}
}
450. Delete nodes in binary search tree
Leetcode link
Given the root node root and a value key of a binary search tree, delete the node corresponding to the key in the binary search tree and ensure that the nature of the binary search tree remains unchanged. Returns a reference to the root node of a binary search tree that may be updated.
Generally speaking, deleting a node can be divided into two steps:
First, find the node to be deleted;
If found, delete it.
Example 1:
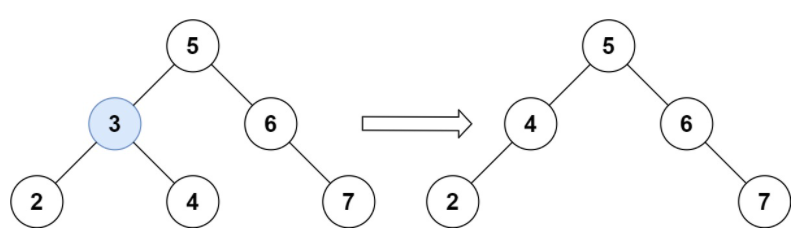
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: given that the value of the node to be deleted is 3, we first find the node 3 and then delete it.
A correct answer is [5,4,6,2,null,null,7], as shown in the figure below.
Another correct answer is [5,2,6,null,4,null,7].
Example 2:
Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: a binary tree does not contain nodes with a value of 0
Example 3:
Input: root = [], key = 0
Output: []
Solution:
- Delete node has no child nodes
- Delete node has no right node
- Delete node has no left node
- There are left and right nodes for deleting nodes. The first three are easy to handle. In example 1, if you delete root node 5, you need to move the left subtree to the left node of node 6 of the right subtree.
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return root;
if (key < root.val) {
root.left = deleteNode(root.left, key);
} else if (key > root.val) {
root.right = deleteNode(root.right, key);
} else {
// The deleted node has been found
TreeNode left = root.left;
// If the right node is empty, return the left node, the left node, and the right node
if (root.right == null) {
return root.left;
} else if (root.left == null) {
return root.right;
} else {
// The left and right are not empty. Put the left subtree in the appropriate position of the right subtree
TreeNode cur = root.right;
// Find the leftmost part of the right subtree
while (cur.left != null) {
cur = cur.left;
}
cur.left = left;
return root.right;
}
}
return root;
}
}
669. Pruning binary search tree
Leetcode link
Give you the root node of the binary search tree, and give the minimum boundary low and the maximum boundary high at the same time. By pruning the binary search tree, the values of all nodes are in [low, high]. Pruning a tree should not change the relative structure of the elements retained in the tree (that is, if they are not removed, the original parent-child relationship should be retained). It can be proved that there is a unique answer. Therefore, the result should return the new root node of the trimmed binary search tree. Note that the root node may change according to a given boundary.
Example 1:
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]
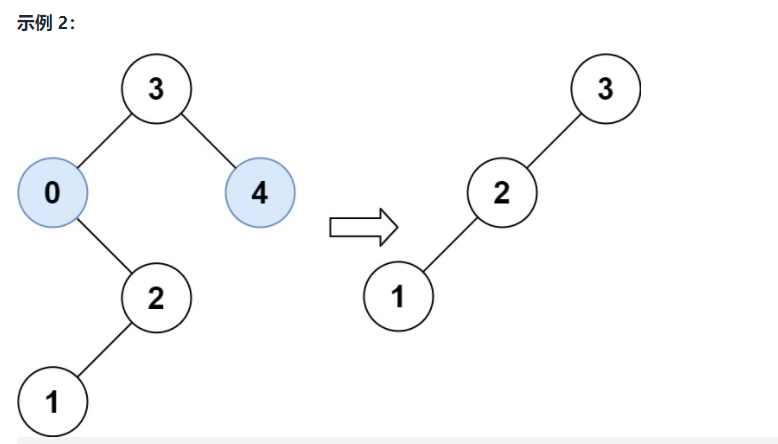
Example 2:
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]
Solution:
Error solution: direct root = = null | root val < low || root. Val > high returns null. Although 0 is less than 1, you cannot directly remove all the left subtrees
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null || root.val < low || root.val > high) return null;
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
}
Method 1: recursive method
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) return root;
if (root.val < low) {
// If 0 is less than 1, skip the left subtree and directly recurse the right subtree greater than 0. The returned fit is equivalent to skipping this layer of nodes
return trimBST(root.right, low, high);
}
if (root.val > high) {
return trimBST(root.left, low, high);
}
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
}
Mode 2: iterative method
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) return root;
// Handle the header node and move the root to the range of [L, R]. Note that it is closed left and closed right
while (root != null && (root.val < low || root.val > high)) {
if (root.val < low) {
root = root.right;
} else {
root = root.left;
}
}
// At this time, root is already in the range of [L, R] and handles the case that the left child element is less than L
TreeNode cur = root;
while (cur != null) {
// Same as example 2
while (cur.left != null && cur.left.val < low) {
cur.left = cur.left.right;
}
cur = cur.left;
}
// At this time, root is already in the range of [L, R] and handles the case that the right child is greater than R
cur = root;
while (cur != null) {
while (cur.right != null && cur.right.val > high) {
cur.right = cur.right.left;
}
cur = cur.right;
}
return root;
}
}
108. Convert an ordered array into a binary search tree
Leetcode link
Give you an integer array nums, in which the elements have been arranged in ascending order. Please convert it into a highly balanced binary search tree. A height balanced binary tree is a binary tree that satisfies the requirement that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1.
Example 1:
Input: 0,9,5 [- nums]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] will also be regarded as the correct answer:
Example 2:
Input: num = [1,3]
Output: [3,1]
Explanation: [1,3] and [3,1] are highly balanced binary search trees.
Solution:
review Modification and construction of binary tree in binary tree chapter
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return build(nums, 0, nums.length);
}
public TreeNode build(int[] nums, int left, int right) {
// There are no nodes in the interval
if (right - left <= 0) {
return null;
}
// There is only one node left in the interval
if (right - left == 1) {
return new TreeNode(nums[left]);
}
// Take the intermediate node as the root node every time
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = build(nums, left, mid);
root.right = build(nums, mid + 1, right);
return root;
}
}
538. Convert binary search tree into cumulative tree
Leetcode link
Give the root node of the binary search tree. The node values of the tree are different. Please convert it into a Greater Sum Tree so that the new value of each node is equal to or greater than the node in the original tree Sum of Val values.
Remind me that the binary search tree meets the following constraints:
The left subtree of a node contains only nodes whose key is less than the node key.
The right subtree of a node contains only nodes whose key is greater than the node key.
The left and right subtrees must also be binary search trees.
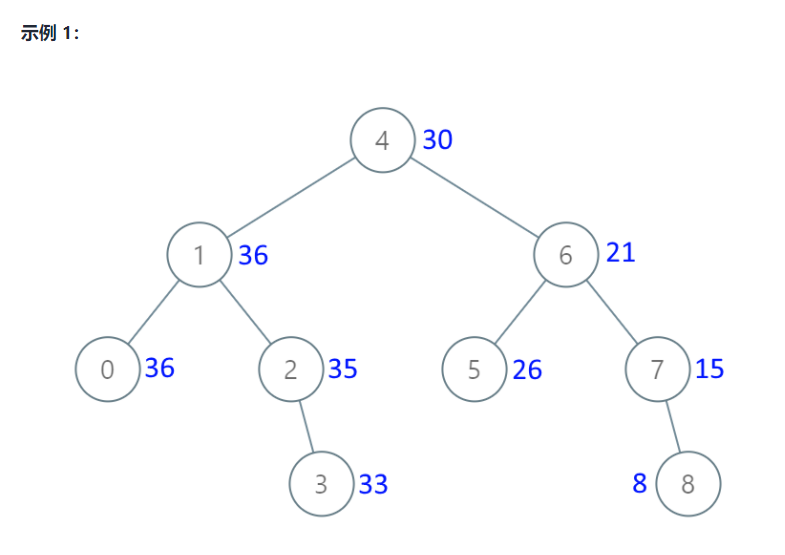
Input: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
Solution:
Middle order traversal
class Solution {
public TreeNode convertBST(TreeNode root) {
dfs(root);
return root;
}
int sum = 0;
public void dfs(TreeNode root) {
if (root == null) return;
// Left
dfs(root.right);
// in
sum += root.val;
root.val = sum;
// right
dfs(root.left);
}
}