Before reading this article, it is recommended to read the blogger's article on red black tree, which describes the evolution from binary sort tree → AVL tree → red black tree. Transmission address: Quick understanding of red and black trees
HashMap source code analysis + interview questions
1, Hash introduction
- Core theory
- Hash is also known as hash and hash. The basic principle is to change the input of any length into the output of fixed length through hash algorithm; The mapping rule is the corresponding hash algorithm, and the binary string mapped by the original data is the hash value
- Characteristics of hash
- The original data cannot be deduced backwards from the hash value
- A small change in the input data will get a completely different hash value, and the same data will get the same value
- The hash algorithm is efficient, and the hash value can be calculated quickly for long text
- The same hash value calculated by the hash algorithm will lead to hash conflict
- Because the principle of hash is to map the value of the input space into the hash space, and the space of hash value is much smaller than the input space, according to the drawer principle, there must be situations where different inputs are mapped into the same output
- Drawer principle: there are ten apples on the table. Put these ten apples in nine drawers. No matter how you put them, we will find that there will be at least two apples in at least one drawer (hash conflict)
2, Introduction to HashMap collection
-
HashMap is based on the Map interface implementation of hash table, which is used to store K-V key value pairs
-
The implementation of HashMap is not synchronous, which means that it is not thread safe
-
The key and value of HashMap can be null
-
The mappings in HashMap are not ordered
-
The speed of query, modification and addition is very fast, and can reach the average time complexity of O(1)
-
Before JDK8, HashMap consists of array + linked list. Array is the main body of HashMap. Linked list is mainly used to solve hash conflict
- Hash conflict means that the hash values calculated by two key s calling the hashCode method are the same, resulting in the same calculated array index values
-
After JDK8, HashMap is composed of array + linked list + red black tree
- When the length of the linked list is greater than or equal to the threshold (8 by default) and the capacity of the array is greater than 64, all data of the linked list is stored in red black tree instead
- Note that it is the capacity of the array, not the actual number of array elements
- The capacity of the array can be understood as the length of the array, excluding the number of nodes of the linked list and red black tree
- When the number of nodes in the black list is less than or equal to 6, the red tree will be restored
- When the length of the linked list is greater than or equal to the threshold (8 by default) and the capacity of the array is greater than 64, all data of the linked list is stored in red black tree instead
-
Before converting the linked list into a red black tree, it will be judged that if the threshold is greater than or equal to 8, but the array length is less than 64, the linked list will not be changed into a red black tree, but the array expansion will be selected
- The default expansion method is to double the capacity of the newly created array, recalculate the index value of the original data and copy it
-
The HashMap structure is shown below
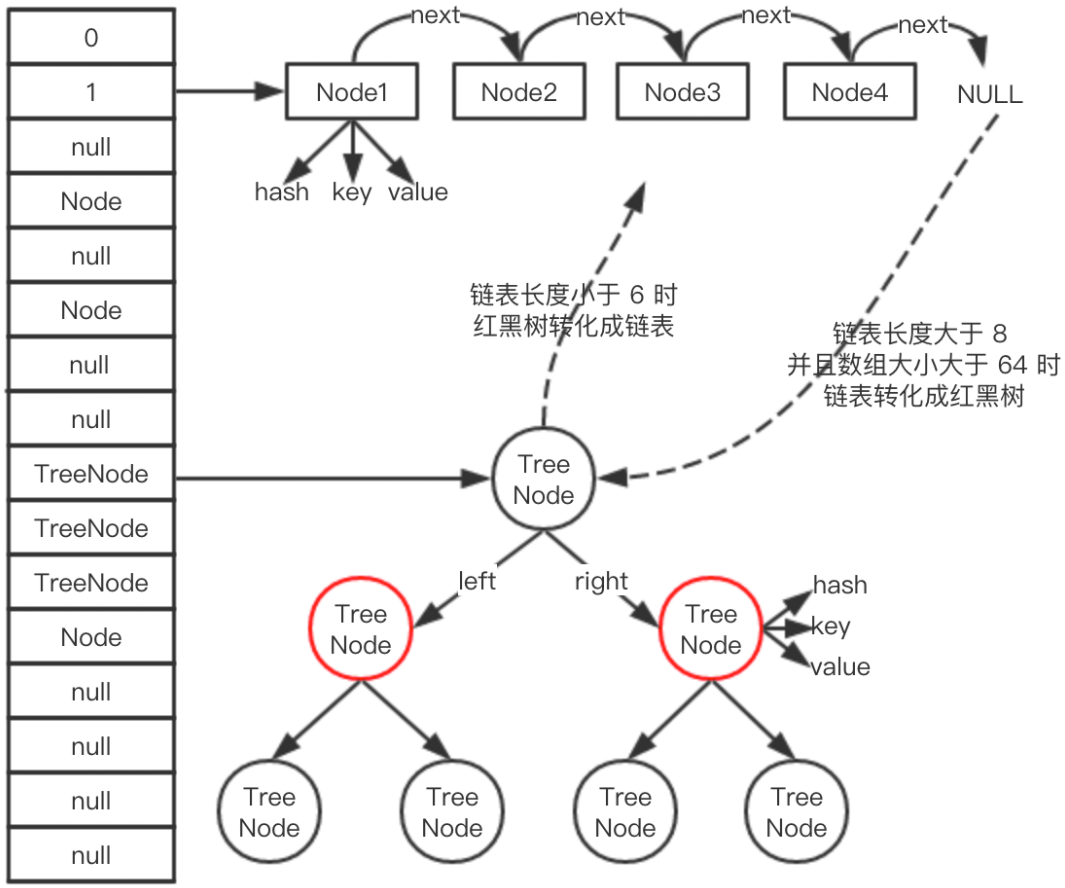
- Standing on the left of the figure is the array structure of HashMap. The elements of the array may be a single Node, a linked list, or a red black tree. For example, the position where the array subscript index is 2 is a linked list, and the position where the subscript index is 9 corresponds to the red black tree
3, HashMap the process of storing data
3.1 process analysis
- Call the null parameter constructor HashMap < string, integer > map = new HashMap < > (); Create a HashMap collection object
- If it is JDK8, when calling the constructor, create a Entry[] table with a length of 16 for storing key value pairs.
- If it is JDK8, the array will not be created when the constructor is invoked, but when the put() method is first invoked, the Node[] table of length 16 is used to store the key value pairs.
- Both entry < K, V > and node < K, V > implement map The entry < K, V > interface is responsible for storing key value pairs
- When adding a K-V key value pair to the HashMap, calculate the hash value according to the hashCode() method rewritten by the String class where the K call is located. After modifying the hash value, use the hash value & (array length - 1) in combination with the array length to calculate the index value of the data stored in the Node array
- If the index position is empty, the key value pair is inserted and added successfully
- If the index position is not empty, first judge the hash value of the inserted element, the hash value of the element at this index position and the key Whether the equals method returns true. If they are all true, you need to replace the old value of the element at the index position with the new value of the inserted element and return the old value. If they are not all true, continue to execute downward
- If the index position is not empty, it indicates that there may be a linked list or red black tree on the array position at this time. If it is a red black tree, this element will be added to the red black tree according to the rules of the red black tree
- If it is a linked list, traverse the linked list in order and compare the hash values of K and all nodes in the linked list (different hash values may produce the same index value)
- If the hash value of K is the same as that of a node, a hash collision occurs
- Call the equals() method of K's class to compare the key values (different data may produce the same hash value)
- If the equals() method returns true, replace the old value with the new value and return the old value
- If the equals() method returns fasle, continue to compare the hash value with the next node
- Call the equals() method of K's class to compare the key values (different data may produce the same hash value)
- If the hash values are different, draw a new node at the end of the linked list to store the K-V key value pair, and then judge whether it needs to be trealized
3.2 common interview questions
-
What algorithm does the underlying hash table use to calculate the index value? What other methods can calculate the index value?
- The hash table uses the hash value calculated by calling the hashCode() method of K Combined with the array length - 1 to calculate the index value by bit and (&)
- You can also use the remainder method to calculate the index value
- For example, if the hash value is 10, the array length is 8, the calculated value of 10% 8 is 2, then the index value is 2
- The efficiency of the remainder method is relatively low and the bit operation efficiency is relatively high
-
What happens when the hashcodes of two objects are equal?
- Hash collision will occur. If the content of the key value is the same, replace the old value. Otherwise, link to the back of the linked list. When the length of the linked list exceeds the threshold 8 and the length of the array is greater than 64, it will be converted into a red black tree
-
When does hash collision occur? What is hash collision? How to solve hash collision?
- As long as the hash value calculated by the key of two elements is the same, hash collision will occur
- jdk8 used linked list to solve hash collision
- After jdk8, use linked list + red black tree to solve hash collision
-
If the hashcode s of two keys are the same, how to store key value pairs?
- hashcode is the same. Compare whether the contents are the same through equals()
- Same: the new value overwrites the previous value
- Different: new key value pairs are added to the hash table
- hashcode is the same. Compare whether the contents are the same through equals()
-
Why is red black tree introduced into JDK8?
-
When hash collisions occur frequently, that is, there are many elements in a linked list, the linked list will be too long. The efficiency of searching by key value in turn is low, and the time complexity is O(n)
-
The search speed of red black tree is very fast, and the time complexity is O(logn), so the reason why red black tree is introduced is to improve the search efficiency
-
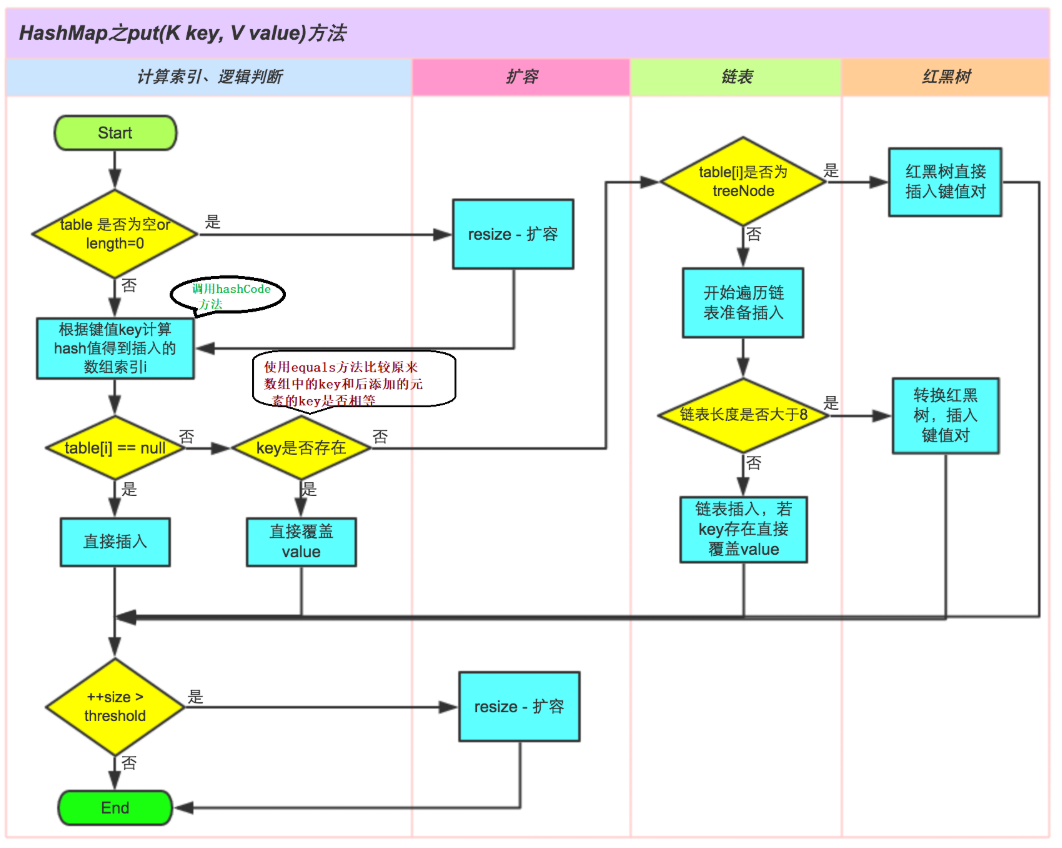
The flow chart of adding data is as follows:
-
Points needing attention
- If you are adding elements for the first time, the array is empty at this time. You need to expand the capacity of the array to 16 first
-
When adding an element to the tail of the linked list, first judge whether it needs to be treelized. If so, convert it into a red black tree and insert the element
- After adding elements in the three methods (direct insertion into array position, red black tree insertion and linked list insertion), you need to judge whether + + size is greater than the capacity expansion threshold. If it is greater than, you need to expand the capacity of the array
-
size indicates the actual number of K-V in the HashMap. Note that this is not equal to the capacity (length) of the array
-
Size not only indicates the number of nodes on the array, but also the nodes of linked list and red black tree are counted as part of size
-
threshold = capacity * loadFactor. When the size exceeds this critical value, the capacity will be resize d. The HashMap capacity after capacity expansion is twice the previous capacity
4, HashMap inheritance relationship
The inheritance relationship of HashMap is shown in the following figure:
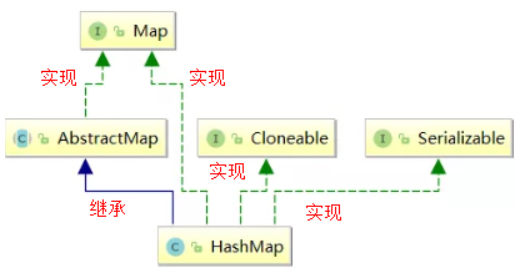
explain:
- Cloneable interface, which means that you can clone. Cloning refers to creating and returning a copy of a HashMap object
- Serializable serialization interface. HashMap objects can be serialized, written on persistent devices and deserialized
- AbstractMap parent class to minimize the work required to implement the Map interface
Supplement:
Through the above inheritance relationship, we find a strange phenomenon that HashMap has inherited AbstractMap and AbstractMap class implements Map interface. Why does HashMap implement Map interface? (this structure is also found in ArrayList and LinkedList)
according to java Founder of collection framework Josh Bloch Description, such writing is a mistake. stay java In the collection framework, there are many ways to write like this, which is written at the beginning java When he set the framework, he thought it might be valuable in some places until he realized he was wrong. obviously JDK Later, the defenders did not think that this small mistake was worth revising, so it existed
5, HashMap collection members
5.1 member variables
- Serialization version number
private static final long serialVersionUID = 362498820763181265L;
- Initialization capacity of the array (the capacity of the array must be the nth power of 2)
//The default initial capacity is 16 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; //1 < < 4 is equivalent to the fourth power of 1 * 2
Question 1: why must the capacity of an array be the nth power of 2?
answer:
The construction method of HashMap overload can also specify the initialization capacity of the array
HashMap(int initialCapacity) //Construct an empty HashMap with a specified initial capacity and a default load factor (0.75)
According to the above explanation, when adding an element to the HashMap, you need to determine its specific position in the array according to the hash value of the key
In order to access HashMap efficiently, it is necessary to minimize collisions, that is, to distribute the data evenly as much as possible, and the length of each linked list is roughly the same
In order to meet the uniform distribution of data, HashMap adopts an algorithm, that is, index position = hash% length (hash is temporarily understood as hash value, and length represents the length of array). The efficiency of direct remainder in the computer is not as good as that of displacement operation, so it is optimized in the source code, using index position = hash & (length-1)
The premise that hash%length is equal to hash & (length-1) is that length is the nth power of 2
Question 2: why is the n-th power of array length 2 able to distribute evenly and reduce collisions?
The binary corresponding to the nth power of 2 is 1, followed by N zeros, and the binary corresponding to the nth power of 2 - 1 is n ones
Example 1:
Assumed array length length When it is 8, it is 2 n Power, the corresponding binary is 1000
calculation length-1 As follows:
1000
- 1
---------
111
1.When the hash value is 3, the hash&(length-1) As follows:
00000011 3 hash
& 00000111 7 length-1
-------------------------
00000011 3 Array subscript
2.When the hash value is 2, the hash&(length-1) As follows:
00000010 2 hash
& 00000111 7 length-1
-------------------------
00000010 2 Array subscript
//Conclusion: when the array length is the n-th power of 2, the collision can be reduced (the index positions of the above two calculations are different)
Therefore, the reason why the hashmap capacity is power-2 is to evenly distribute the data and reduce hash conflicts. After all, the greater the hash conflict, the greater the length of a chain in the representative array, which will reduce the performance of hashmap
Example 2:
When the array length is 9(Not 2 n pow ),9-1 The value is 8, the corresponding binary is 1000, and the last three bits are 0. Since it is an and operation, no matter hash How do the last three digits of the value change? The last three digits of the calculated value must be 0, for example hash When it is 2 or 3 respectively, the calculated index value is 0, and hash collision occurs
//Conclusion: the length of the array is required to be the nth power of 2. The purpose is to change the last few bits of the binary into 1 after subtracting one. Because it is an and operation, the result of the and operation of the last few bits depends on the size of the hash value, reducing hash collision
Note: if the efficiency is not considered, the remainder can be obtained directly (there is no need to require that the array length must be the nth power of 2)
Question 3: what if the specified array initialization capacity is not the nth power of 2? Like 10?
answer:
HashMap will modify the specified capacity to be greater than or equal to the nearest power 2 of the specified capacity through displacement operation and or operation
The source code analysis is as follows:
//Create the object of HashMap collection, and specify that the length of the array is 10, not power 2
HashMap hashMap = new HashMap(10);
//Called constructor
//The parameter value is 10
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR); //The value of parameter 1 is 10 and the value of parameter 2 is 0.75
}
//Called constructor
//Parameter 1 is 10 and parameter 2 is 0.75
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY) //MAXIMUM_ Capability is 2 ^ 30
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
//None of the three if statements were executed
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
//Call the tableSizeFor method, the parameter value is 10, and modify 10 to the nearest number greater than or equal to the second power of 10, that is, 16
}
//Called tableSizeFor method
//The parameter value is 10
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
Analysis of tableSizeFor() method:
-
Why do you want to reduce cap first? int n = cap - 1;
- If the cap is already a power of 2, but the minus 1 operation is not performed, the capacity will be twice that of the cap after performing the following unsigned right shift operations
- However, it is enough to directly use the number given to the power of 2, which does not need to be doubled, resulting in a waste of space
-
If after cap-1, n becomes 0, then after several unsigned right shifts, it is still 0, and the last returned value is 1 (there is an n+1 operation at last), but here we only discuss the case that n is not equal to 0
-
Analysis of shift right operation
First shift right:
int n = cap - 1; //cap=10 n=9 n |= n >>> 1; 00000000 00000000 00000000 00001001 //9 (integer 4 bytes, 8 bits per byte, so 32 bits) | 00000000 00000000 00000000 00000100 //9 changes to 4 after moving to the right -------------------------------------------------------- 00000000 00000000 00000000 00001101 //Bitwise XOR is followed by 13
Since n is not equal to 0, there will always be a bit of 1 in the binary of N. at this time, the highest bit 1 is considered. By shifting 1 bit to the right without symbol, the highest bit 1 is shifted to the right by 1 bit, and then do or operation, so that the right bit immediately adjacent to the highest bit 1 in the binary of n is also 1, such as:
00000000 00000000 00000000 00001001 Become 00000000 00000000 00000000 00001101 //Is to change the penultimate place to 1
Second shift right:
n |= n >>> 2; //N becomes: n=13 through the first right shift 00000000 00000000 00000000 00001101 //13 | 00000000 00000000 00000000 00000011 //13 changes to 3 after moving to the right -------------------------------------------------------- 00000000 00000000 00000000 00001111 //Bitwise XOR followed by 15When n is shifted to the right by two unsigned bits, the two consecutive ones in the highest order will be shifted to the right by two bits, and then it will do or operate with the original n. in this way, there will be four consecutive ones in the binary high order of N, such as:
00000000 00000000 00000000 00001101 Become 00000000 00000000 00000000 00001111
Third shift right:
n |= n >>> 4; //N becomes: n=15 through the first and second right shifts 00000000 00000000 00000000 00001111 //15 | 00000000 00000000 00000000 00000000 //15 changes to 0 after moving right -------------------------------------------------------- 00000000 00000000 00000000 00001111 //Bitwise XOR followed by 15This time, shift the four consecutive ones in the existing high order to the right by 4 bits, and then do or operation. In this way, there will normally be eight consecutive ones in the high order represented by the binary of n, but at this time, all of them have been shifted successfully, so there are only four consecutive ones
The value of 15 + 1 is 16, so the return value is 16, that is, the specified capacity 10 is modified to 16
be careful:
-
The maximum capacity is a positive number of 32bit, so in the end, n | = n > > > 16, the capacity is up to 32 1s (but this is already a negative number)
-
In order to have 32 1s, the highest bit of 32bit must be 1, that is, the initialCapacity is 2 ^ 31
-
However, before executing tableSizeFor, the initialCapacity will be judged. If it is greater than MAXIMUM_CAPACITY(2 ^ 30), then MAXIMUM_CAPACITY, because it is the n-th power of 2, the capacity is still 2 ^ 30 after tablesize for
-
The value returned by the tableSizeFor() method is assigned to threshold (capacity expansion threshold)
this.threshold = tableSizeFor(initialCapacity); //The return value is 16
You may wonder why the result of tableSizeFor should be assigned to the capacity expansion threshold? I'll explain later
-
-
The default load factor is 0.75
static final float DEFAULT_LOAD_FACTOR = 0.75f;
- Maximum capacity of array
//The upper limit of the maximum capacity of the array is: the 30th power of 2 static final int MAXIMUM_CAPACITY = 1 << 30;
- Threshold for converting linked list into red black tree (added in 1.8)
//When the number of nodes in the linked list exceeds 8 and the length of the array exceeds 64, the linked list will be converted into a red black tree static final int TREEIFY_THRESHOLD = 8;
Question 1: why does the number of nodes in the HashMap bucket exceed 8 before it is converted into a red black tree?
- Bucket refers to a certain position of the array. The bucket can be a linked list or a red black tree
answer:
-
The node space of the red black tree is twice that of the linked list node
-
When the length of the linked list reaches 8, it will be converted into a red black tree. When the red black tree node is reduced to 6, it will be restored into a linked list
-
The time complexity of linked list query is O (n), and the query complexity of red black tree is O (logn)
-
When there is not much data in the linked list, it is also faster to use the linked list for traversal. Only when there is more data in the linked list, it will be transformed into a red black tree
-
The reason why red black trees are not used at the beginning is to save space
-
According to the Poisson distribution formula, due to the uniform distribution of nodes, the possibility of the number of linked list nodes reaching 8 is very low. Therefore, using 8 as the threshold, the number of linked list nodes less than 8 can not only ensure the query speed, but also not prematurely convert to red black tree and occupy more storage space
-
When writing code and using HashMap normally, you will hardly encounter the case that the linked list is transformed into a red black tree. After all, the probability is only one in ten million
- Threshold value of red black tree restoring to linked list
//When the number of nodes in the red black tree is less than 6, it will be restored to a linked list static final int UNTREEIFY_THRESHOLD = 6;
- Threshold of array capacity converted to red black tree
//When the length of the linked list is greater than 8 and the length of the array is greater than 64, all the data of the linked list is stored in red black tree instead static final int MIN_TREEIFY_CAPACITY = 64; //In order to avoid the conflict of capacity expansion and tree selection, this value cannot be less than 4 * tree_ THRESHOLD (8)
- An array of storage elements (the capacity must be the nth power of 2)
transient Node<K,V>[] table;
- Set set for storing key value pairs
transient Set<Map.Entry<K,V>> entrySet;
- The number of elements actually stored in the array (including linked list and red black tree) (not equal to the capacity of the array)
transient int size; //Maybe not (because the thread is unsafe, it may change when you get this value)
- Record the modification times of HashMap
//The HashMap structure will be incremented by 1 every time it is added, expanded, or modified transient int modCount;
- Expansion critical value
//When the number of actual elements in the array exceeds the critical value of capacity expansion, capacity expansion will be carried out int threshold; //(capacity * load factor) the default is 16 * 0.75 = 12
- Loading factor
//The default value is 0.75 final float loadFactor;
-
The loading factor indicates the density of the HashMap
-
The method to calculate the real-time loading factor of HashMap is: size / capacity
-
The loading factor value of 0.75f is a good critical value given by the official
-
When the elements contained in the array have reached 75% of the length of the array, it means that the HashMap is too crowded and needs to be expanded. The process of capacity expansion involves rehash, copying data and other operations, which is very performance consuming. Therefore, the number of capacity expansion can be minimized in development. You can avoid capacity expansion by specifying the initial capacity when creating HashMap collection objects
//Specify initialization capacity and load factor HashMap(int initialCapacity, float loadFactor);
Question 2: why is the value of the load factor set to 0.75f?
answer:
The closer the loadFactor approaches to 1, the more data (entries) stored in the array will be, and the more dense it will be, which will increase the length of the linked list. The smaller the loadFactor is, that is, it will approach 0, and the less data (entries) stored in the array will be, and the more sparse it will be
give an example:
The load factor is 0.4, So 16*0.4--->6 If the array is expanded when it is full of 6 spaces, the utilization rate of the array will be too low The load factor is 0.9, So 16*0.9--->14 Then this will lead to a little more linked lists, This leads to low efficiency in finding elements
- Therefore, both the array utilization and the number of linked list nodes should not be too many. After a lot of tests, the loading factor of 0.75 is the best scheme
- Node of linked list
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
//....
}
- Red black tree node
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent;
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev;
boolean red;
//....
}
5.2 construction method
- Construct an empty HashMap with default initial capacity (16) and default load factor (0.75)
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR;
//After JDK8, the array will be created when the put method is used
//Create array in constructor before JDK8
//Here is JDK8
}
- Construct a HashMap with a specified initial capacity and a default load factor (0.75)
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
//Call the constructor of two parameters
}
- It is suggested in Alibaba Java development manual that initialization capacity = number of key value pairs to be stored / 0.75F + 1.0F
- Construct a HashMap with a specified initial capacity and load factor
public HashMap(int initialCapacity, float loadFactor) {
//Judge whether the initialization capacity is less than 0
if (initialCapacity < 0)
//If it is less than 0, an illegal parameter exception, IllegalArgumentException, is thrown
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
//If the initial array capacity exceeds maximum_ Capability, the maximum_ Capability is assigned to initialCapacity
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
//Judge whether the load factor loadFactor is less than or equal to 0 or whether it is a non numeric value
if (loadFactor <= 0 || Float.isNaN(loadFactor))
//If one of the above conditions is met, an illegal parameter exception IllegalArgumentException will be thrown
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
//Assign the specified load factor to the HashMap member variable
this.loadFactor = loadFactor;
//Call the tableSizeFor method to modify the array capacity to the power of 2, as mentioned earlier
//The return value of the tableSizeFor method is assigned to the array expansion threshold
this.threshold = tableSizeFor(initialCapacity);
}
be careful:
For this threshold = tableSizeFor(initialCapacity); Assign the modified array capacity to the array expansion threshold. You may think that if you want to meet the definition of expansion threshold, the writing method should be this threshold = tableSizeFor(initialCapacity) * this. loadFactor; ; However, it should be noted that all constructors do not initialize the table array. When the put() method creates a table, the value of threshold will be recalculated
- Constructor containing another Map
//Construct a new HashMap with the same mapping relationship as the specified Map
public HashMap(Map<? extends K, ? extends V> m) {
this.loadFactor = DEFAULT_LOAD_FACTOR; //Use the default load factor of 0.75
putMapEntries(m, false); //Call the putMapEntries method
}
Explanation of putMapEntries() method:
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
//m represents the specified parameter Map set, and the evict value is false
//Get the actual capacity of parameter Map
int s = m.size();
//If the actual capacity of the parameter Map is less than or equal to 0, nothing will be done
if (s > 0) {
//If the current HashMap array has not been created, you need to create a new array
if (table == null) {
//Get the capacity of the newly created array. Actual number of elements / loading factor = = array capacity
//Why add 1? I'll explain later
float ft = ((float)s / loadFactor) + 1.0F;
//Determine the size of the array capacity and the maximum array capacity
int t = ((ft < (float)MAXIMUM_CAPACITY) ?
(int)ft : MAXIMUM_CAPACITY);
//If the array capacity is greater than the expansion threshold of the current HashMap, call tableSizeFor to modify the array capacity to the power of 2
//The capacity expansion threshold is int type, and the default value is 0
if (t > threshold)
//Assigned to capacity expansion threshold
threshold = tableSizeFor(t);
}
//If the actual capacity of the parameter Map is greater than the capacity expansion threshold of the current HashMap, the HashMap needs to be expanded
else if (s > threshold)
resize();
//This shows that HashMap has an array and the array capacity is sufficient
//Add all key value pairs in the parameter Map to the array of HashMap
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
K key = e.getKey();
V value = e.getValue();
//The putVal method will be explained later
putVal(hash(key), key, value, false, evict);
}
}
}
Question: why float ft = ((float)s / loadFactor) + 1.0F; Do you want to perform the + 1 operation?
answer:
- The purpose is to obtain larger array capacity, so as to reduce the number of capacity expansion
give an example:
- Assuming that the actual number of elements in the parameter Map is 6, then 6 / 0.75 is 8, which is the n-th power of 2, then the new array size is 8. However, this will lead to insufficient capacity when storing elements. If you continue to expand the capacity, the performance will be reduced
- After + 1, the length of the array is changed to 16 directly through the tableSizeFor() method, which can reduce the number of array expansion
5.3 membership method
5.3.1 adding method
- The put() method is as follows:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
//First, call the hash method to modify the hash value of the key
//Then call the putVal method.
}
- The hash() method is as follows:
static final int hash(Object key)
{
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
//1. The key value can be null and the hash value is 0, that is, the element with null value is always located at the position where the array index is 0
//2. If the key is not equal to null, first calculate the hashCode of the key and assign it to h, and then move the binary of H and h to the right without sign by 16 bits to perform bitwise XOR to obtain the final hash value
//3. In other words, when calculating the index value of the array analyzed previously, the index position = hash% length. Hash is not the hash value of key, but the hash value after XOR operation
}
Analysis of (H = key. Hashcode()) ^ (H > > > 16) and hash% length process:
-
key.hashCode() calculates the hash value of the key, assuming that the hash value at this time is 1111 1111 1111 1111 0000 1110 1010
-
Assuming that the length value of the array at this time is 16, length-1 is 1111
-
The operation process is as follows:

-
The calculated index value of the array is 5
-
In general, the high 16 bit does not change, and the low 16 bit and high 16 bit do an XOR. Why do you do this?
If you use hash value and array length directly-1 Doing and Computing: hashCode()Value: 1111 1111 1111 1111 1111 0000 1110 1010 & length-1,I.e. 15: 0000 0000 0000 0000 0000 0000 0000 1111 ------------------------------------------------------------------- 0000 0000 0000 0000 0000 0000 0000 1010 ---->10 As an index //It can be found that if the length of the array is small, the sum operation is only performed in the low order, and the high order is all 0. If the low order of the hash value of the next key does not change, but only the high order changes, the calculated index value will be consistent with the above, as follows: For example, for the newly inserted hash value, the 6th and 7th bits of the high order are changed: 1111 1001 1111 1111 1111 0000 1110 1010 & 0000 0000 0000 0000 0000 0000 0000 1111 ---------------------------------------------------------- 0000 0000 0000 0000 0000 0000 0000 1010 ---->10 A hash conflict occurred as an index //Therefore, the high and low bits are used to avoid hash conflict, so as to prevent the same index value obtained when only the high bits change
- The putVal() method is as follows:
//The user calls the put method, and the put method calls the putVal method
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
/**
* Parameter Description:
* hash: hash Hash value after shift right + XOR operation in method
* key: K of key value pair
* value: V of key value pair
* onlyIfAbsent: The value is false, which means that the old value of this node will be replaced with the new value
* evict: The value is true, indicating
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//Determine whether the array is empty
if ((tab = table) == null || (n = tab.length) == 0)
//If it is empty, call the resize method to create an array. The default length is 16
n = (tab = resize()).length;
//Judge whether the index position of the array corresponding to the Key is empty. If it is empty, create a new node and assign it to the corresponding array position
//According to the previous description, I = (n - 1) & hash is used to calculate the index value of the array corresponding to the key
if ((p = tab[i = (n - 1) & hash]) == null)
//The fourth parameter of the newNode method represents the next pointer, pointing to the next node in the linked list
tab[i] = newNode(hash, key, value, null);
//If the array position corresponding to the Key is not empty, it indicates that there may be a linked list or red black tree on the position
else {
Node<K,V> e; K k;
//p indicates the existing node in the array position at this time
//Compare the hash value of the two, the address value of the key and the actual value of the key
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
//This indicates that the old value will be replaced with the new value. p indicates the existing node in the array position at this time
e = p;
//Follow this instruction to compare in the linked list or red black tree
//Judge whether the linked list has been trealized at this time. If it is trealized, the node will be inserted in the way of red black tree
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
//Follow this instruction to insert a node into the linked list
else {
//Loop through all nodes of the linked list
for (int binCount = 0; ; ++binCount) {
//If you have traversed the last node at this time, create a new node and insert it at the end of the linked list
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
//If the number of linked list nodes is greater than or equal to 8, it may be treelized
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash); //The tree method will be explained later
break;
}
//Whether the code block of the first if is executed or not, the condition of the first if will be executed
//At this time, e represents the next node of the linked list
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
//To replace the old value with the new value
break;
p = e; //Move to next node
}
}
//If e= Null, the old value will be replaced with the new value and the old value will be returned
if (e != null) {
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
//Each call to put increments the counter by one
++modCount;
//If you do not replace the old value, you need to set size+1
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
5.3.2 process of adding new nodes in red black tree
The process of putTreeVal() method is as follows:
-
Starting from the root node, first judge whether the new node already exists in the red black tree. The judgment methods are as follows:
1.1 if the node does not implement the Comparable interface, use equals to judge
1.2 if the node implements the Comparable interface, use compareTo to judge
-
If the new node is already in the red black tree (the hash value and key value are the same), it will be returned directly, and the new value will be used to replace the old value in the putVal() method; If not, judge whether the new node is on the left or right of the current node:
2.1 if the hash value of the new node is less than the hash value of the current node, it is on the left
2.2 if the hash value of the new node is greater than the hash value of the current node, it is on the right
2.3 if a direct return is found, replace the old value with the new value in the putVal() method
-
Spin recursion steps 1 and 2. Stop spinning until the node on the left or right of the current node is empty. The current node is the parent node of the new node
-
Place the new node where the left or right of the current node is empty, and establish a parent-child node relationship with the current node
-
Shade and rotate, end
5.3.3 tree method
Process: first convert all the nodes of the linked list into the nodes of the red black tree and connect them together, then replace the position of the linked list on the array with the red black tree, and finally balance the red black tree
/**
* Parameter Description:
* tab: array
* hash: hash Hash value after shift right + XOR operation in method
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
//If the array has not been created, call resize() to create the array
//If the number of linked list nodes is greater than or equal to 8 but the array capacity is less than 64, call resize() to expand the capacity
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
//Follow this description to meet the two conditions for converting the linked list into a red black tree
//Execute else if code block when there is a linked list in the bucket
else if ((e = tab[index = (n - 1) & hash]) != null) {
//hd represents the head node of the red black tree and tl represents the tail node of the red black tree
TreeNode<K,V> hd = null, tl = null;
//Convert each node of the linked list into a node of the red black tree, and the stored content is consistent
do {
//The replacementTreeNode method converts nodes, which will be explained later
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p; //The first node after conversion becomes the head node and tail node of the red black tree
else {
//Connect the transformed red black tree nodes in two-way connection. p represents the newly added node and tl represents the existing tail node
p.prev = tl;
tl.next = p;
}
tl = p; //The newly added node becomes the tail node
} while ((e = e.next) != null); //Traverse down the nodes of the linked list
//Follow this instruction to convert all nodes in the linked list into red black tree nodes and connect the nodes together
//However, at this time, the node is only converted successfully, and the red black tree has not been connected to the position of the array and is not balanced
//if conditions connect the red black tree created above to the corresponding position of the array, balance the red black tree and replace the linked list
if ((tab[index] = hd) != null)
//Rotate the created red black tree to make it balanced
hd.treeify(tab);
}
}
The replacementTreeNode() method is as follows:
TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) {
return new TreeNode<>(p.hash, p.key, p.value, next);
}
5.3.4 capacity expansion method
If you want to understand the source code of the expansion method, you must first clarify two knowledge points:
-
When will the expansion be needed?
- If the size exceeds the capacity expansion threshold, the capacity will be expanded
- If the number of linked list nodes is greater than or equal to 8, but the array length is less than 64, the capacity will be expanded
-
What is the process of capacity expansion?
-
The default capacity expansion method is to double, corresponding to the binary. Move the original highest 1 forward by 1 bit. After the length is reduced by 1, the corresponding binary is 1 bit more forward than the original
-
You also need to recalculate the new index values of all nodes (including those on the linked list) by calling hash & (n-1), as shown in the following figure:

-
As can be seen from the above figure, when calculating the new index value, you only need to pay attention to the value of the hash value of the key corresponding to the bit (1) that moves the array capacity forward, because it is the same operation. If the hash value of the key is 0, the index value obtained is still the same as that without capacity expansion; If this bit of the hash value of the key is 1, the index value obtained after the operation will be one more bit forward, that is, "original location + old capacity", as shown in the following figure:
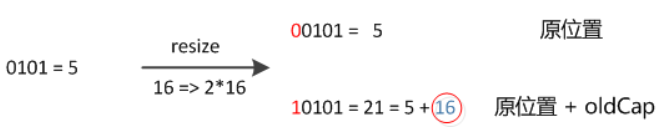
-
The benefits of doing so
- The time for recalculating the hash value is saved
- Whether the hash value of the key corresponding to the new 1 bit is 0 or 1 can be considered as random, and the previous conflicting nodes can be evenly dispersed into the new bucket
-
Use a chart to illustrate the calculation of the new index value
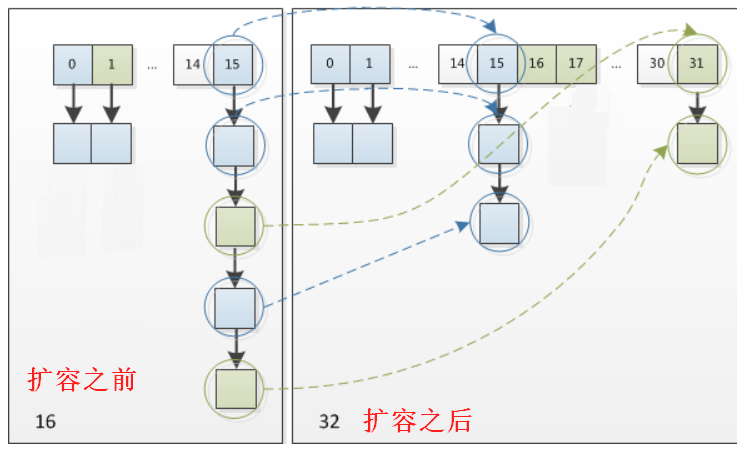
- It can be seen that if the bucket position is a linked list, the original linked list will be divided into two linked lists, named high-level linked list and low-level linked list respectively. If the node belongs to low-level linked list, the new index value is the same as the original; If the node belongs to the high-order linked list, the new index value is the original position + old capacity. Which linked list a node belongs to depends on whether the bit value of the high-order is 1 or 0
- After one bucket is processed, the next bucket can be processed
- There are two loops. The first loop traverses the position of the array, and the second loop traverses the linked list or red black tree of the position of the array
-
The source code of resize() method is as follows:
final Node<K,V>[] resize() {
//Save the information of the old array
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
//When the old array is not empty
if (oldCap > 0) {
//If the capacity of the old array is greater than or equal to the maximum capacity, it will never be expanded
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
//Multiply the capacity of the old array by 2 to become the capacity of the new array
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
//If the capacity of the old array is less than 16, it will not be executed, that is, newThr will not be assigned a value of 0
//When the conditions are met, double the capacity expansion threshold to a new capacity expansion threshold
newThr = oldThr << 1;
}
//If the old array is empty but the capacity expansion threshold is greater than 0, the capacity expansion threshold is assigned to the capacity of the new array
//Note that the new expansion threshold is not assigned
else if (oldThr > 0)
newCap = oldThr;
//If the old array and expansion threshold are empty, the new array uses the default value
else {
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
//If the above first else if is not executed, then newThr == 0
//When the old array is empty, the second else if is executed, and the newThr is not assigned, and the value is 0
//The capacity expansion threshold needs to be calculated
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr; //Determine the new expansion threshold as the threshold of the new array
//Create a new expanded array
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
//Calculate the new index value of the data in the original array and add it to the newly created expanded array
if (oldTab != null) {
//Traverse the nodes in the old array
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
//Take out the node of the old array and assign it to e
if ((e = oldTab[j]) != null) {
oldTab[j] = null; //Set the corresponding position of the old array to null to facilitate garbage collection
//If the location of the old array bucket has only one node
if (e.next == null)
//Insert this node into the index position corresponding to the new array
newTab[e.hash & (newCap - 1)] = e;
//If the location of the old array bucket has become a red black tree, call split to split the red black tree
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
//The position of the bucket is a linked list
else {
//Low linked list
Node<K,V> loHead = null, loTail = null;
//High order linked list
Node<K,V> hiHead = null, hiTail = null;
//Record the next node of the linked list
Node<K,V> next;
do {
next = e.next; //Record the next node of the linked list
//The if condition does not use the length minus one to execute and operate. At this time, the highest bit of the old capacity must be 1
//Doing so will extract whether the high-order hash value of the node is 1 or 0
//If it is 0, this node belongs to the low linked list
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
//If the high order is 1, this node belongs to the high order linked list
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null); //Traverse down the nodes of the original linked list
//If there is a low order linked list, move its head node to the same index position of the new array as the original array
if (loTail != null) {
loTail.next = null; //Prevent the last node of the low-level linked list from pointing to a node of the original linked list
newTab[j] = loHead;
}
//If there is a high-order linked list, move its head node to the original position of the new array + the index position of the old capacity
if (hiTail != null) {
hiTail.next = null; //Prevent the last node of the high-order linked list from pointing to a node of the original linked list
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab; //Returns the newly created expanded array that successfully moves the original node
}
5.3.5 split process of red black tree
The process of split() method is as follows:
The processing method is similar to the linked list, which is to divide the node into high-level linked list and low-level linked list. If the node belongs to low-level linked list, the new index value is the same as the original; If the node belongs to the high-order linked list, the new index value is the original position + old capacity, and then moves to the position of the new array. The difference is:
- The split high-low linked list needs to judge the length of the linked list
- If the length is less than or equal to 6, directly convert the TreeNode into an ordinary Node linked list, and then put it into the new array after capacity expansion
- If the length is greater than 6, you need to upgrade the linked list to a red black tree (rebuild the red black tree)
5.3.6 deletion method
When deleting, first find the array position of the element. If the corresponding index position is the node to be deleted, delete and return; If it is a linked list, traverse the linked list, delete and return after finding the elements. If it is a red black tree, traverse the red black tree, delete and return after finding the elements. When the number of red black tree nodes is less than 6, it should be turned into a linked list
The source code of the remove() method is as follows:
public V remove(Object key) {
Node<K,V> e;
//First, call the hash method to get the modified hash value corresponding to the key, which is consistent with the put method
//Then call the removeNode method to delete and return the corresponding node
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
The source code of removeNode() method is as follows:
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
//If the array exists and the corresponding position of the array is not empty
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
//Node indicates the node to be deleted
Node<K,V> node = null, e; K k; V v;
//If the corresponding position of the array is the node to be deleted
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p; //Assign the deleted node to node
//If the corresponding position of the array is not the node to be deleted, judge whether there is a linked list or red black tree. If so, traverse the linked list or red black tree to find the node to be deleted and assign it to node
//e represents the linked list corresponding to the array position node or the last node of the red black tree
else if ((e = p.next) != null) {
//If there are red and black trees
if (p instanceof TreeNode)
//Call the getTreeNode method to traverse the red black tree, find the corresponding node and assign it to node
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
//If there is a linked list, traverse the linked list to find the node and return it to node
else {
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null); //Traverse down the linked list
}
}
//If there are nodes to be deleted
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
//If the node of the red black tree is deleted, call the removeTreeNode method to delete the node according to the rules of the red black tree
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
//If the node on the array is deleted
else if (node == p)
tab[index] = node.next;
//If the node on the linked list is deleted
else
p.next = node.next;
++modCount; //Counter plus 1
--size; //size-1
afterNodeRemoval(node);
return node; //Returns the deleted node
}
}
//If the array is empty or the corresponding array position is empty, null is returned
return null;
}
5.3.7 query method
When querying, first find the array position of the element. If the corresponding index position is the node to be found, return; If it is a linked list, traverse the linked list and return after finding the elements. If it is a red black tree, traverse the red black tree and return after finding the elements
The source code of get() method is as follows:
public V get(Object key) {
Node<K,V> e;
//First, call the hash method to get the modified hash value corresponding to the key, which is consistent with the put method
//Then call the getNode method to get the corresponding value
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
The source code of getNode() method is as follows:
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
//If the array exists and the corresponding position of the array is not empty
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
//If the corresponding array position is the node to be found, return the node
if (first.hash == hash &&
((k = first.key) == key || (key != null && key.equals(k))))
return first;
//If the corresponding position of the array is not the node to be searched, judge whether there is a linked list or red black tree. If so, traverse the linked list or red black tree to find the node to be searched and return
//e represents the linked list corresponding to the array position node or the last node of the red black tree
if ((e = first.next) != null) {
//If it's a red black tree
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
//If it's a linked list
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null); //Traverse down the linked list
}
}
//If there is no node to find, null is returned
return null;
}
5.3.8 node searching process of red black tree
- Recursive lookup from root node
- Compare the hash values of the lookup node and the current node. If the hash values are the same and the key s are the same, find and return the current node; If the hash values are different, it is determined whether to search in the left subtree or the right subtree according to the comparison results
- Judge whether there are locating nodes in step 2. If there are, return. If not, repeat steps 2 and 3
- Spin until the node location is found. If it is not found, null is returned
6, HashMap time complexity analysis
The time complexity of query and insertion is O(1)
reason:
- First, find the position of the array. Using the characteristics of the array, the time complexity is O(1)
- The location of the bucket may be a linked list or a red black tree
- If it is a linked list with no more than 8, it is considered that the time complexity is also O(1)
- According to Poisson distribution, the probability of becoming a red black tree is only one in ten million, so it is considered that the time complexity is still O(1)
- The time complexity of insertion is the same