java backend to achieve addition, subtraction, multiplication, division and proportion calculation

In Java The math package provides the API class BigDecimal, which is used to accurately calculate the number of more than 16 significant bits.
BigDecimal creates objects, so you cannot directly perform mathematical operations on its objects using arithmetic operators such as +, -, *, /, etc.

First of all, you need to understand that BigDecimal has four construction methods:

	//Creates an object with an integer value specified by the parameter
	BigDecimal(int)
	//Creates an object with the double value specified by the parameter
	BigDecimal(double)
	//Creates an object with an integer value specified by the parameter
	BigDecimal(long)
	//Creates an object with the value specified by the parameter as a string
	BigDecimal(String)

	//Here, two forms are compared. The first one directly writes the value of a number, and the second one is represented by a string
	BigDecimal num1 = new BigDecimal(0.005);
    BigDecimal num2 = new BigDecimal(1000000);
    BigDecimal num3 = new BigDecimal(-1000000);    
    //Try to initialize in the form of string
    BigDecimal num12 = new BigDecimal("0.005");
    BigDecimal num22 = new BigDecimal("1000000");
    BigDecimal num32 = new BigDecimal("-1000000");

1. Addition, subtraction, multiplication and division

	//add()
    BigDecimal result1 = num1.add(num2);
    BigDecimal result12 = num12.add(num22);
 
    //Subtraction subtract()
    BigDecimal result2 = num1.subtract(num2);
    BigDecimal result22 = num12.subtract(num22);
 
    //multiply()
    BigDecimal result3 = num1.multiply(num2);
    BigDecimal result32 = num12.multiply(num22);
 
    //Absolute value (ABS)
    BigDecimal result4 = num3.abs();
    BigDecimal result42 = num32.abs();
 
    //divide()
    //Num1, num12 divisor, 20 exact decimal places, BigDecimal ROUND_ HALF_ Up rounding mode
    BigDecimal result5 = num2.divide(num1,20,BigDecimal.ROUND_HALF_UP);
    BigDecimal result52 = num22.divide(num12,20,BigDecimal.ROUND_HALF_UP);

Here, you can see the result by outputting all the results
There are differences here, which is why string is recommended for initialization

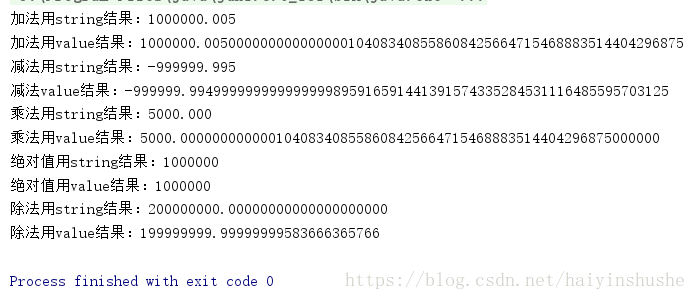
※ note:

1)System. out. The number in println () is double by default, and the decimal calculation of double is inaccurate.

2) When the BigDecimal class construction method is used to pass in the double type, the calculation result is also inaccurate!

Because not all floating-point numbers can be accurately represented as a double value, some floating-point numbers cannot be accurately represented as a double value, so it will be represented as the value of the double type closest to it. You must use the constructor of the incoming String instead. This is explained in the constructor annotation of BigDecimal class.

Use the divide() parameter

When using the division function to divide, set various parameters, accurate decimal places and rounding mode, or an error will appear
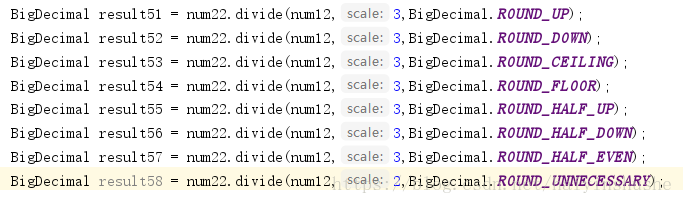
We can see that the parameters configured for the divide function are as follows

	//That is (BigDecimal divisor, int scale exact decimal places, int roundingMode rounding mode)
	Public BigDecimal divide(BigDecimal divisor, int scale, int roundingMode)

But there are many rounding modes BigDecimal ROUND_ XXXX_ 30. What exactly does that mean

The eight rounding modes are explained below

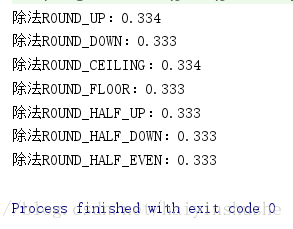
1)ROUND_UP

Rounding away from zero.

Always increase the number before discarding the non-zero part (always add 1 to the number before the non-zero discarding part).

Note that this rounding mode never reduces the size of the calculated value.

2)ROUND_DOWN

Rounding mode close to zero.

Never increase the number before discarding a part (never increase the number before discarding a part by 1, i.e. truncate).

Note that this rounding mode never increases the size of the calculated value.

3)ROUND_CEILING

Rounding pattern close to positive infinity.

If BigDecimal is positive, the rounding behavior is the same as ROUND_UP is the same;

If negative, the rounding behavior is the same as round_ Same as down.

Note that this rounding mode never reduces the calculated value.

4)ROUND_FLOOR

Rounding mode close to negative infinity.

If BigDecimal is positive, the rounding behavior is the same as round_ Same as down;

If the bold style is negative, the rounding behavior is the same as round_ Same as up.

Note that this rounding mode never increases the calculated value.

5)ROUND_HALF_UP

Round to the "closest" number. If the distance from two adjacent numbers is equal, it is the rounding mode of rounding up.

If the discard part > = 0.5, the rounding behavior is the same as ROUND_UP is the same; Otherwise, the rounding behavior is the same as round_ Same as down.

Note that this is the rounding pattern (rounding) that most of us learned in primary school.

6)ROUND_HALF_DOWN

Round to the "closest" number. If the distance from two adjacent numbers is equal, it is the rounding mode of rounding up.

If the discard part > 0.5, the rounding behavior is the same as ROUND_UP is the same; Otherwise, the rounding behavior is the same as round_ Same as down (rounded).

7)ROUND_HALF_EVEN

Round to the "closest" number, or even if the distance from two adjacent numbers is equal.

If the number to the left of the discarded part is odd, the rounding behavior is the same as ROUND_HALF_UP is the same;

If it is an even number, the rounding behavior is the same as round_ HALF_ Same as down.

Note that this rounding mode minimizes cumulative errors when repeating a series of calculations.

This rounding model, also known as "banker rounding method", is mainly used in the United States. Round to the nearest five.

If the previous digit is odd, round it, otherwise round it.

The following example is the result of this rounding method if 1 decimal place is reserved.

1.15>1.2 1.25>1.2

8)ROUND_UNNECESSARY

Assert that the requested operation has a precise result and therefore does not need to be rounded.

If this rounding mode is specified for an operation that obtains a precise result, an ArithmeticException is thrown.

For example: calculate the result of 1 ÷ 3 (the last ROUND_UNNECESSARY will report an error when the result is an infinite decimal)

2. Compare size

	//The premise is that neither a nor b can be null
	BigDecimal a = new BigDecimal("xx");
    BigDecimal b = new BigDecimal("xx");
	
	if(a.compareTo(b) == -1){
	    System.out.println("a less than b");
	}
	 
	if(a.compareTo(b) == 0){
	    System.out.println("a be equal to b");
	}
	 
	if(a.compareTo(b) == 1){
	    System.out.println("a greater than b");
	}
	 
	if(a.compareTo(b) > -1){
	    System.out.println("a Greater than or equal to b");
	}
	 
	if(a.compareTo(b) < 1){
	    System.out.println("a Less than or equal to b");
	}

Good law: everything will be good in the end. If it's not good, it's not the end.