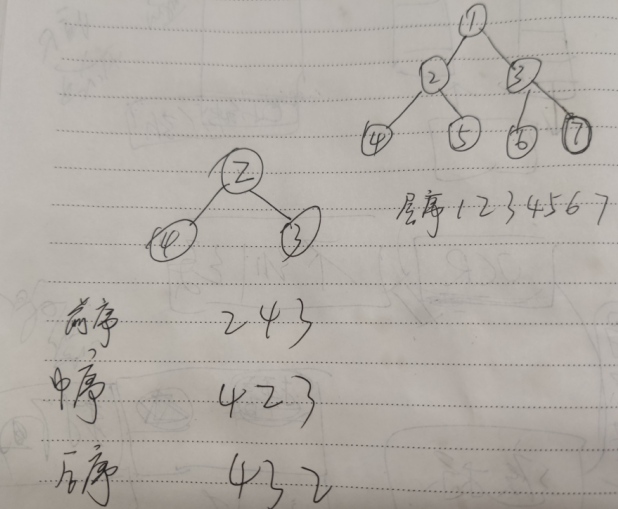
Let's start with sequence traversal. This is a common problem. Print it according to each layer, as follows:

For Recommendation in Deep learning QQ Group 277356808

For deep learning QQ Second Group 629530787

I'm here waiting for you

1 - sequence traversal and deformation

Sequence traversal is the most intuitive and simplest sequence, that is, from top to bottom and from left to right, as shown in the figure below

class Solution(object):
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root: return [] #Note the special case: if the tree is empty, return []
        queue = [root]
        list1 = []
        while queue:
            list2 = []
            for i in range(len(queue)):
                a = queue.pop(0)#Element out of queue
                if a.left:
                    queue.append(a.left)
                if a.right:
                    queue.append(a.right)
                list2.append(a.val)
            list1.append(list2)
        return list1

Deformation: the first line is from left to right, the second line is from right to left, and so on, that is, odd lines are from left to right, and even lines are from right to left. How to change the code: add reverse and it's OK?? If you say you can't play like that, I won't

    def levelOrder2(self, root):#Print by odd or even lines
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root: return [] #Note the special case: if the tree is empty, return []
        queue = [root]
        list1 = []
        flag=1
        while queue:
            list2 = []
            for i in range(len(queue)):
                a = queue.pop(0)#Element out of queue
                if a.left:
                    queue.append(a.left)
                if a.right:
                    queue.append(a.right)
                list2.append(a.val)
            if flag%2:#Odd rows from left to right
                list1.append(list2)
            else:#Even rows from right to left
                list1.append(list2[::-1])
            flag+=1
        return list1

The tests are as follows:

tree=TreeNode()
tree.left=TreeNode(2)
tree.right=TreeNode(4)
tree.left.left=TreeNode(1)
tree.left.right=TreeNode(3)
tree.right.left=TreeNode(7)
tree.right.right=TreeNode(6)

>>> Solution().levelOrder(tree)
[[0], [2, 4], [1, 3, 7, 6]]
>>> Solution().levelOrder2(tree)
[[0], [4, 2], [1, 3, 7, 6]]

The judgment of odd and even lines and the flipping increase new complexity. Although there is no difference in the whole, it is still not very good. It may not meet the requirements of some people. Please see Source of the original question , the following answer is OK

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        res, deque = [], collections.deque([root])
        while deque:
            tmp = collections.deque()
            for _ in range(len(deque)):
                node = deque.popleft()
                if len(res) % 2: tmp.appendleft(node.val) # Even layer - > queue header
                else: tmp.append(node.val) # Odd layer - > end of queue
                if node.left: deque.append(node.left)
                if node.right: deque.append(node.right)
            res.append(list(tmp))
        return res

2-search the maximum subtree sum of binary tree. This is not found

The sum of the largest binary tree is found without the word "search". emm, I give this binary tree as a search binary tree, and try to see if the result is correct,

class Solution:
    def __init__(self):
        self.maxSum = -2**31
    def findMaxSubTree(self, root, maxRoot):
        if root == None:
            return 0
        # Find the sum of all nodes of the left subtree of root
        lmax = self.findMaxSubTree(root.left, maxRoot)
        # Find the sum of all nodes of the right subtree of root
        rmax = self.findMaxSubTree(root.right, maxRoot)
        sums = lmax + rmax + root.val
        # The sum of subtrees with root as the root is greater than the maximum value calculated above
        if sums > self.maxSum:
            self.maxSum = sums
            maxRoot.val = root.val
        # Returns the sum of all nodes of the subtree with root as the root node
        return sums
sol=Solution()
m=TreeNode(0)
>>> sol.findMaxSubTree(tree,m)
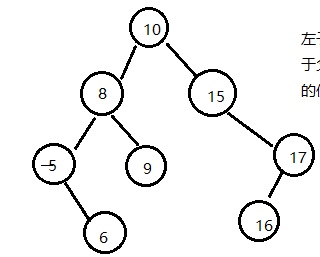
23

Tested, right?? Search the binary tree as follows, [search the binary tree, where the order traversal result is the sorting result]

def inOrder(root):
    if not root:return
    inOrder(root.left)
    print(root.val,";")
    inOrder(root.right)
Tree=TreeNode(10)
Tree.left=TreeNode(8)
Tree.right=TreeNode(15)
Tree.left.left=TreeNode(-5)
Tree.left.right=TreeNode(9)
Tree.left.left.right=TreeNode(6)

Tree.right.right=TreeNode(17)
Tree.right.right.left=TreeNode(16)
>>> inOrder(Tree)#An illustrative example is the search binary tree
-5 ;
6 ;
8 ;
9 ;
10 ;
15 ;
16 ;
17 ;

>>> sol.findMaxSubTree(Tree,m)
76

The largest search for the sum of subtrees of binary tree should be the result of removing - 5 and 6?? No, it's worth plus 1.. It should be included. What about changing - 5 to - 8? Try it. It won't work. - 8 will also be included, because there are three numbers: 9 and 6. Try - 100

The result is: an obvious mistake

>>> sol.findMaxSubTree(Tree,m)
-19

3-The minimum lexicographically ordered subsequence of length k in the string (meaning that it can be discontinuous but keep the order before and after, while the substring is continuous)

First give two awesome operations, as follows: thank the big guys in the group who helped me

>>> import string
>>> string.ascii_lowercase
'abcdefghijklmnopqrstuvwxyz'

>>> list(string.ascii_lowercase)
['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']

>>> ''.join(list(string.ascii_lowercase))
'abcdefghijklmnopqrstuvwxyz'

The corresponding java language is toCharArray, String()

In addition, the size of dictionary order can be directly determined in py or java. Build another dictionary out of order (the dictionary representing order), as shown below

>>> low=string.ascii_lowercase
>>> for i in range(len(low)-1):
	if low[i]<low[i+1]:
		print(True)

		
True
. . . 

I translated the java version from the Internet into py. The translation results have been compared with java and there are no errors. As follows PY

def findMinMapOrderSubStr(inStr,k):
    size=len(inStr)
    s=inStr[size-k:]#
    print(s)
    chs=list(s)
    for i in range(size-k-1,-1,-1):
        s=""
        pre=inStr[i]
        for j in range(k):
            ch=chs[j]
            if ch<pre:
                break
            else:
                chs[j]=pre
                pre=ch
    return ''.join(chs)

But I suspect there are errors, and the original version of java is wrong, as shown in the following example

>>> findMinMapOrderSubStr('abcdafg',3)
'aaf'

Please comment. Questions or amendments are welcome.

May we finally meet again, and you still remember the topic we discussed.