Learn from https://labuladong.gitee.io/algo/2/19/36/
1, DFS implements topology sorting
Immediately above: why do you need to reverse the result of post order traversal to get the result of topological sorting?
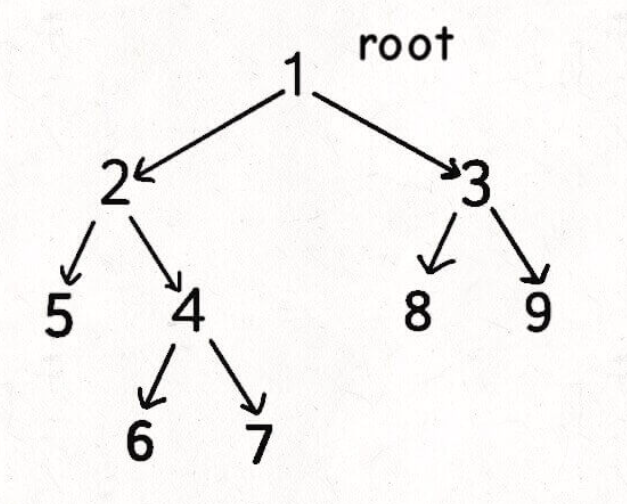
Take the above binary tree as a directed graph and point from the root node to the left and right child nodes. Then, the root node will only be traversed in the last subsequent traversal. For example, for the left child of node 1, the sequence of subsequent traversal should be: 5 6 7 4 2, and 2 is the root node. Therefore, according to the definition of topological sorting, 2 should be output in the first position, That's why we need to reverse the order.
Note that there are codes on the Internet that do not need to be reversed. This is because the definition of "edge" is different. Here, we define edge 1 - > 2, which means that 1 is dependent on 2 and can be repaired only after 1 is repaired. If it is changed to 2 - > 1, it means that 2 depends on 1 and depends on 1. Only after 1 is repaired can 2 be repaired.
In order to make the question easy to understand, the first definition method selected only needs to reverse at the end, which doesn't take much time.
Next, you can start writing code, first build a diagram, judge whether there is a ring, and reverse the subsequent traversal results.
class Solution {
// Avoid repeated visits
boolean[] vis;
// Record the current access path
boolean[] onPath;
// Is there a ring
boolean hasCycle = false;
// Record the subsequent traversal results
List<Integer> order = new ArrayList<>();
public int[] findOrder(int numCourses, int[][] prerequisites) {
// Build map first
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
// ergodic
vis = new boolean[numCourses];
onPath = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
// Because the nodes of the graph in the title may not be connected (each into a lump)
// So you need to traverse each node
traverse(graph, i);
}
// If there is a ring, there can be no result
if (hasCycle) {
return new int[]{};
}
// The result of traversal in reverse order is the answer
Collections.reverse(order);
int[] res = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
res[i] = order.get(i);
}
return res;
}
// DFS traversal
void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
// The node currently traversed is the node on the current traversal path
hasCycle = true;
}
if (vis[s] || hasCycle) {
return;
}
// Preorder traversal position
vis[s] = true;
onPath[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// Record post order traversal position
order.add(s);
onPath[s] = false;
}
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// numCourses nodes
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] t : prerequisites) {
// [1,0], 0 - > 1. Only after 0 is repaired can 1 be repaired
int from = t[1];
int to = t[0];
// Generate edge
graph[from].add(to);
}
return graph;
}
}
Although the code looks many, the logic should be very clear. As long as there is no ring in the graph, we will call the traverse function to perform DFS traversal on the graph, record the post order traversal results, and finally reverse the post order traversal results as the final answer. If you encounter other DAG s, you can also use the same method, and finally reverse the post order traversal results.
2, BFS implements topology sorting
BFS realizes topological sorting, which is more like a method of simulating manual topological sorting. It realizes the detection of rings and the generation of topological sorting through penetration. Each time, all nodes with penetration of 0 are queued first, which can be used as the starting point of topological sorting. These nodes are ejected from the queue in turn (the order of ejecting nodes is the result of topological sorting), The entry degree of the node connected to the current node - can be added to the queue if the entry degree is reduced to 0 in the process of entry degree.
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
// Build map first
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
// Calculated penetration
int[] indegree = new int[numCourses];
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
//[1,0], from 0 to 1, you need to repair 0 first and then 1, so the penetration of 1++
indegree[to]++;
}
// Initialize the nodes in the queue according to the penetration
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) {
// Join = 0, join the team
q.offer(i);
}
}
// Record the results of topology sorting
int[] res = new int[numCourses];
// Indexes
int count = 0;
// Execute BFS algorithm
while (!q.isEmpty()) {
int cur = q.poll();
// The order of pop-up nodes is the result of topological sorting
res[count++] = cur;
for (int next : graph[cur]) {
// The penetration of the node connected to the current node --;
indegree[next]--;
if (indegree[next] == 0) {
q.offer(next);
}
}
}
if (count != numCourses) {
// There are rings and no topological sorting
return new int[] {};
}
return res;
}
// Mapping
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// numCourses nodes
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] t : prerequisites) {
// [1,0], 0 - > 1. Only after 0 is repaired can 1 be repaired
int from = t[1];
int to = t[0];
// Generate edge
graph[from].add(to);
}
return graph;
}
}
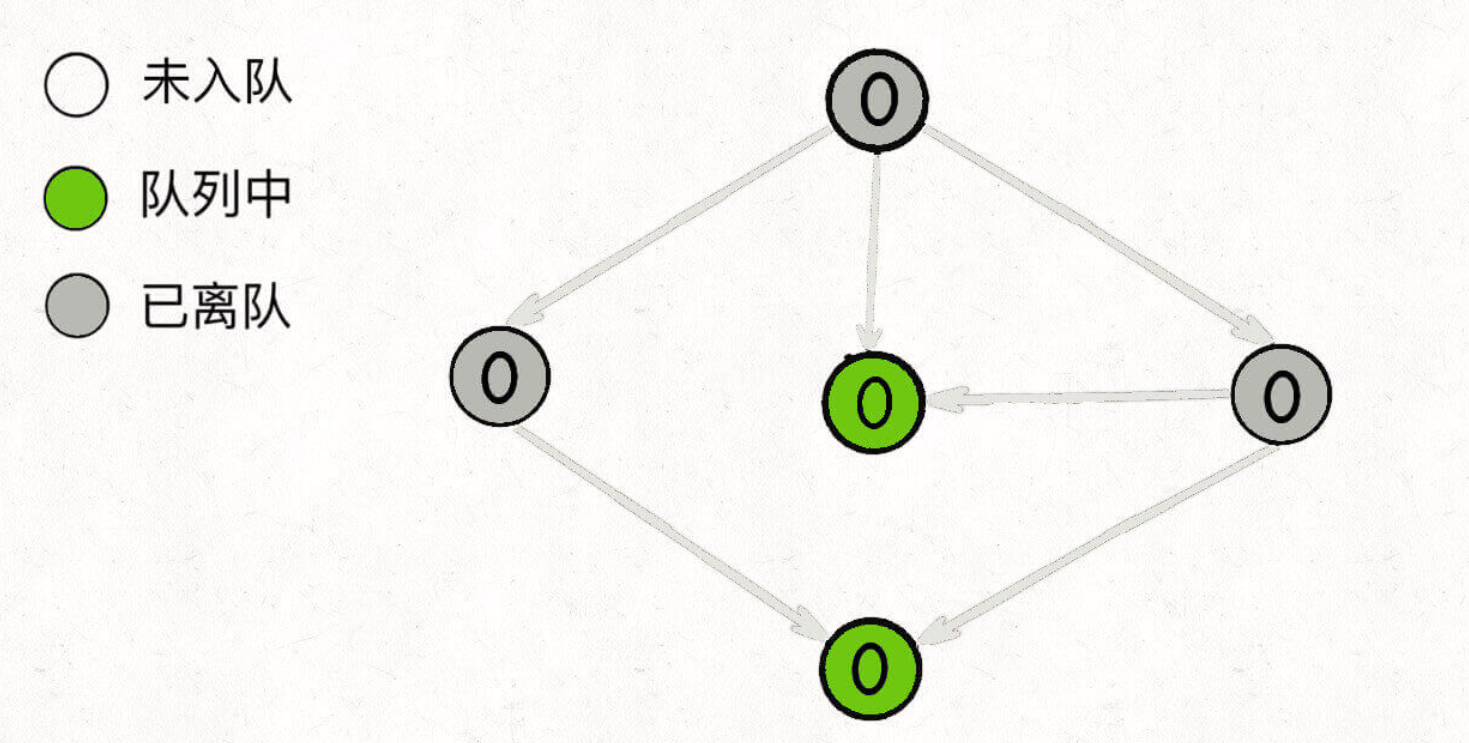
Logically, the traversal of the graph requires the visited array to prevent turning back. The BFS algorithm here is actually realized through the indegree array. The function of the visited array is that only the nodes with a degree of 0 can join the queue, so as to ensure that there will be no dead cycle.
Personally, I suggest to focus on mastering the dfs method, which is more practical and applicable.
3, Bipartite graph decision
Decision idea of bipartite graph
The algorithm for determining bipartite graph is very simple. It is to solve the "two-color problem" with code.
To put it bluntly, it is to traverse the graph and dye it while traversing to see if you can dye all nodes with two colors, and the colors of adjacent nodes are different.
Since the traversal graph does not involve the shortest path, of course, both DFS algorithm and BFS can be used. DFS algorithm is more commonly used, so let's take a look at how to use DFS algorithm to determine bichromatic graph.
Let's review the traversal code in the following figure:
void traverse(int[][] graph, int s) {
// Mark the visited nodes with visited to prevent repeated access
if (visited[s]) {
return;
}
visited[s] = true;
// Traversal preamble
for (int t : graph[s]) {
traverse(graph, t);
}
// Post order traversal code
}
Reviewing how to judge a bipartite graph is actually to let the traverse function traverse the nodes while coloring the nodes, trying to make the colors of each pair of adjacent nodes different.
Therefore, the code logic for determining the bipartite graph can be written as follows:
/* Graph traversal framework */
void traverse(Graph graph, boolean[] visited, int v) {
visited[v] = true;
// Traverse all adjacent nodes of node v
for (int neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// Neighboring nodes have not been accessed
// Then the node neighbor should be painted with a different color from node v
traverse(graph, visited, neighbor);
} else {
// Neighboring nodes have been accessed
// Then you should compare the colors of node neighbor and node v
// If they are the same, then this graph is not a bipartite graph. return directly to save time
}
}
}
Dyeing, use a color to record the color of each node.
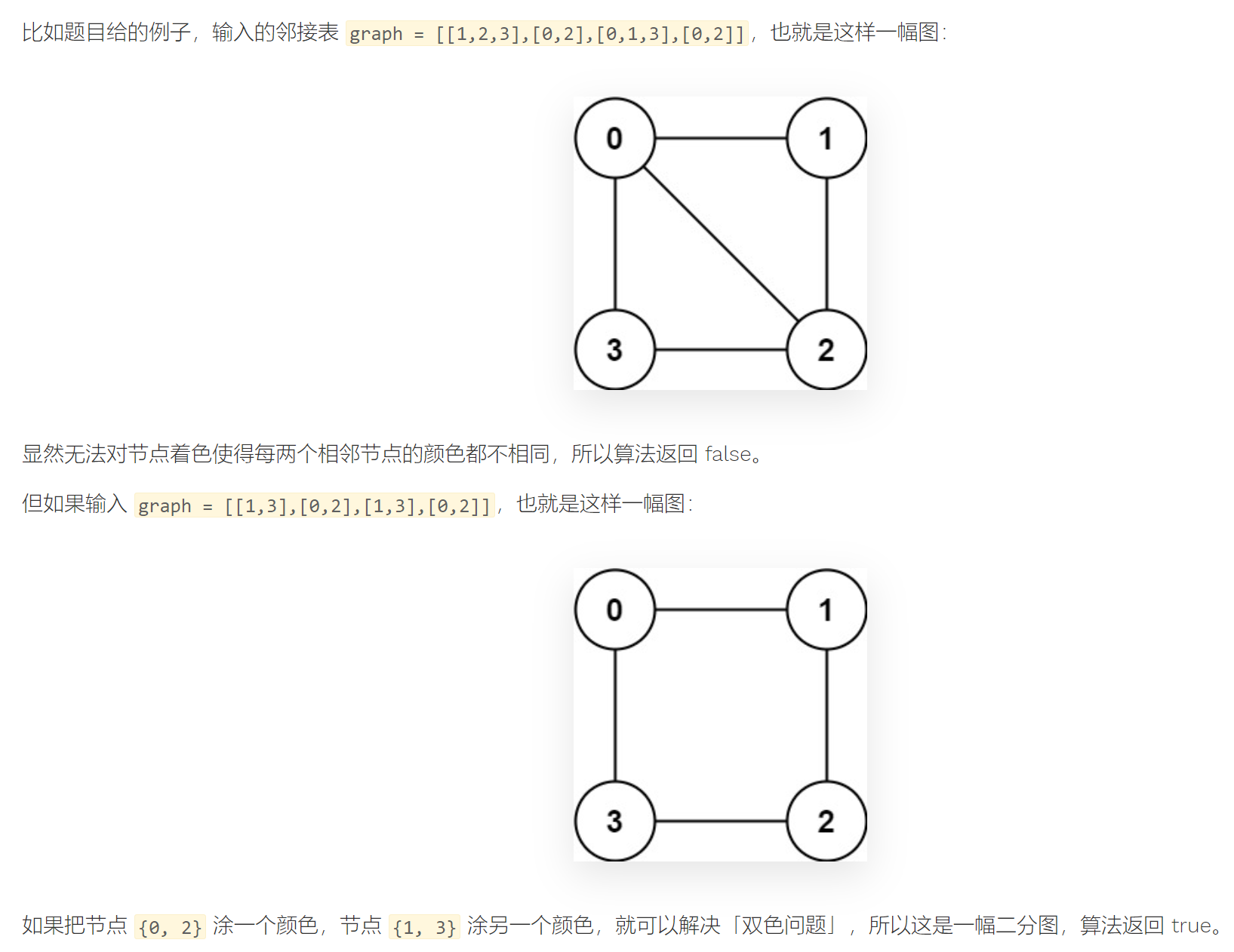
Judgement bipartite graph (medium)

class Solution {
boolean[] vis;
boolean[] colored;
boolean flag = true;
public boolean isBipartite(int[][] graph) {
vis = new boolean[graph.length];
colored = new boolean[graph.length];
// First write the code of traversal graph
// The graph is not necessarily connected, and there may be multiple subgraphs, so each node should be traversed
// If any subgraph is not bipartite, the whole graph is not bipartite
for (int i = 0; i < graph.length; i++) {
if (!vis[i]) {
traverse(graph, i);
}
}
return flag;
}
void traverse(int[][] graph, int s) {
// It's not a bipartite graph, so you don't have to look for it anymore
if (flag == false) return;
vis[s] = true;
for (int t : graph[s]) {
if (vis[t]) {
// If you have visited, it depends on whether the color is the same as that of the current node s
if (colored[t] == colored[s]) {
// It's not a bipartite graph, so you don't have to look for it anymore
flag = false;
return;
}
} else {
// If you haven't visited, paint the opposite color to the current s node
colored[t] = !colored[s];
traverse(graph, t);
}
}
}
}
It can also be solved by BFS, which is the process of BFS traversing the graph
// Whether the recording graph conforms to the nature of bipartite graph
boolean ok = true;
// Record the colors of nodes in the graph. false and true represent two different colors
boolean[] color;
// Record whether the nodes in the graph have been accessed
boolean[] visited;
public boolean isBipartite(int[][] graph) {
int n = graph.length;
color = new boolean[n];
visited = new boolean[n];
for (int v = 0; v < n; v++) {
if (!visited[v]) {
// Use BFS function instead
bfs(graph, v);
}
}
return ok;
}
// Start BFS traversal from the start node
private void bfs(int[][] graph, int start) {
Queue<Integer> q = new LinkedList<>();
visited[start] = true;
q.offer(start);
while (!q.isEmpty() && ok) {
int v = q.poll();
// Spread from node v to all adjacent nodes
for (int w : graph[v]) {
if (!visited[w]) {
// Adjacent nodes w have not been accessed
// Then node w should be painted in a different color from node v
color[w] = !color[v];
// Mark w nodes and put them in the queue
visited[w] = true;
q.offer(w);
} else {
// Adjacent nodes w have been accessed
// Judge whether it is a bipartite graph according to the colors of v and w
if (color[w] == color[v]) {
// If they are the same, this graph is not a bipartite graph
ok = false;
}
}
}
}
}
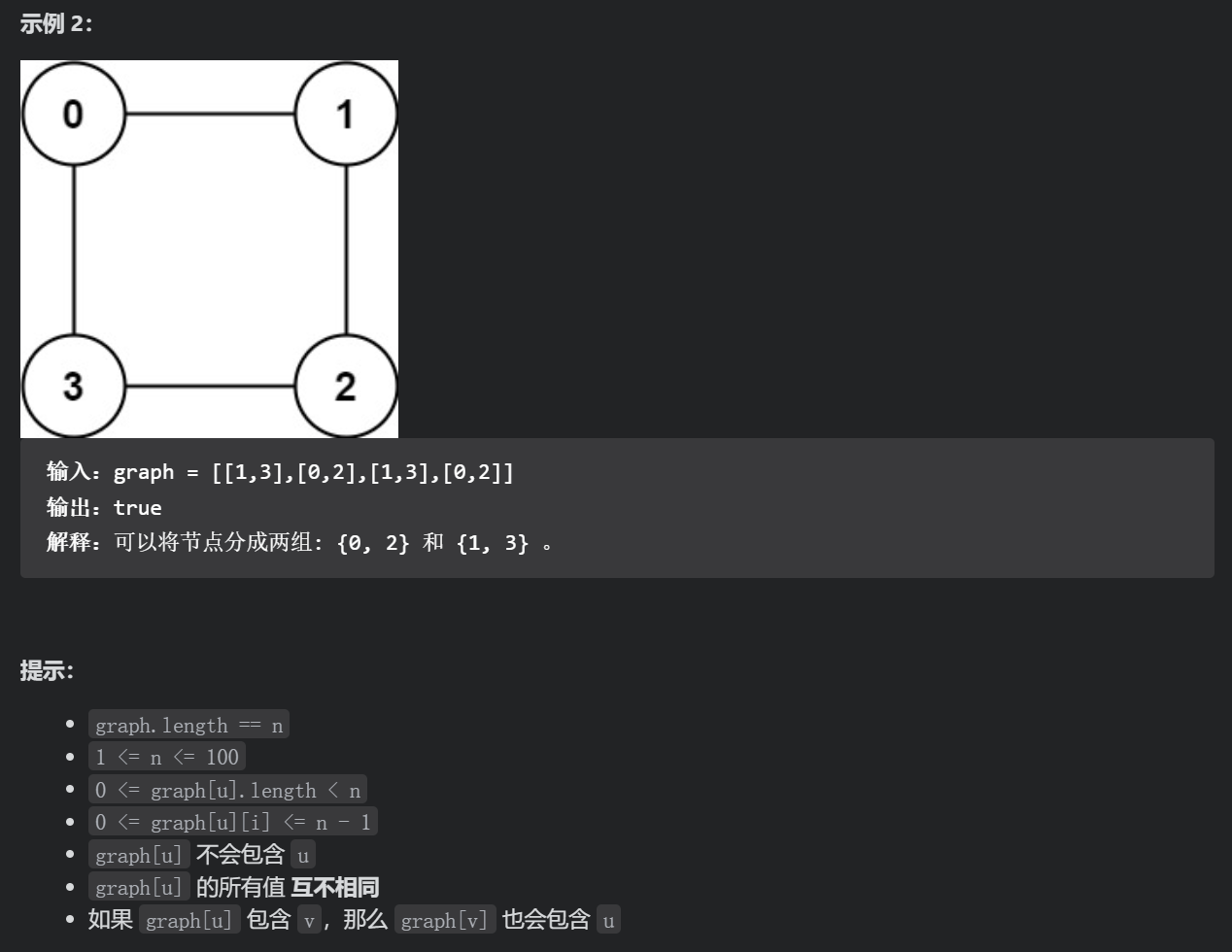
Possible dichotomy (medium)
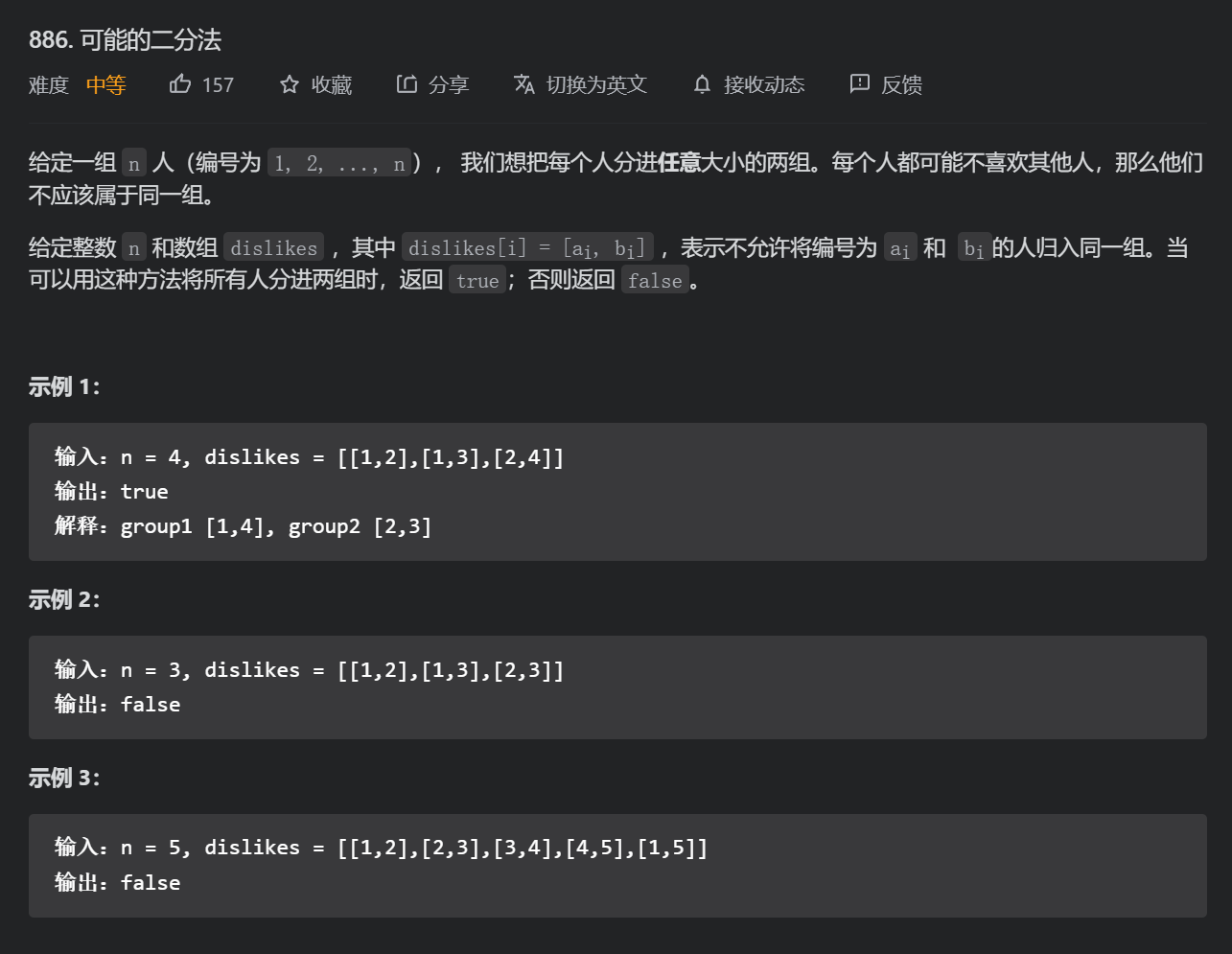

ai and bi cannot be grouped together because they are dislike. If you can divide everyone into two groups, it means they can be divided into two groups. We can represent each dislike group with an undirected graph. If there are only two groups, it is equivalent to two colors. It is not equivalent to judging whether the current graph structure is a bipartite graph. If so, it means that it can be divided into two groups.
Note that when building an undirected graph, two edges should be recorded!
class Solution {
// Final answer
boolean flag = true;
// Record the nodes visited in the past
boolean[] vis;
// Record the color of every second node
boolean[] colored;
public boolean possibleBipartition(int n, int[][] dislikes) {
List<Integer>[] graph = buildGraph(n, dislikes);
vis = new boolean[n + 1];
colored = new boolean[n + 1];
// There may be subgraphs, which are not all connected, so we need to traverse each node
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
traverse(graph, i);
}
}
return flag;
}
void traverse(List<Integer>[] graph, int s) {
// It is impossible to be a bipartite graph. Return directly
if (flag == false) {
return;
}
// Don't forget to mark the visited nodes
vis[s] = true;
for (int t : graph[s]) {
if (vis[t]) {
// After visiting, you can see whether the color of this node is the same as that of the current node s
if (colored[t] == colored[s]) {
flag = false;
// It can't be a bipartite graph anymore. return directly
return;
}
} else {
// Mark the color as the opposite color without visiting
colored[t] = !colored[s];
// Continue to traverse down
traverse(graph, t);
}
}
}
List<Integer>[] buildGraph(int n, int[][] dislikes) {
List<Integer>[] graph = new LinkedList[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new LinkedList<>();
}
for (int[] t : dislikes) {
int from = t[0];
int to = t[1];
// Very error prone!
// Note that the undirected graph should record two edges!!!!
graph[from].add(to);
graph[to].add(from);
}
return graph;
}
}
4, Kruskal minimum spanning tree algorithm
If a picture has no rings, it can be stretched into the shape of a tree. Technically speaking, a tree is an acyclic connected graph.
So what is the "spanning tree" of a graph? In fact, it can be understood literally, that is, to find a tree in the graph that contains all the nodes in the graph. Professionally speaking, a spanning tree is an "acyclic connected subgraph" containing all vertices in a graph.
It's easy to think that a picture can have many different spanning trees. For example, in the following picture, the red edge forms two different spanning trees
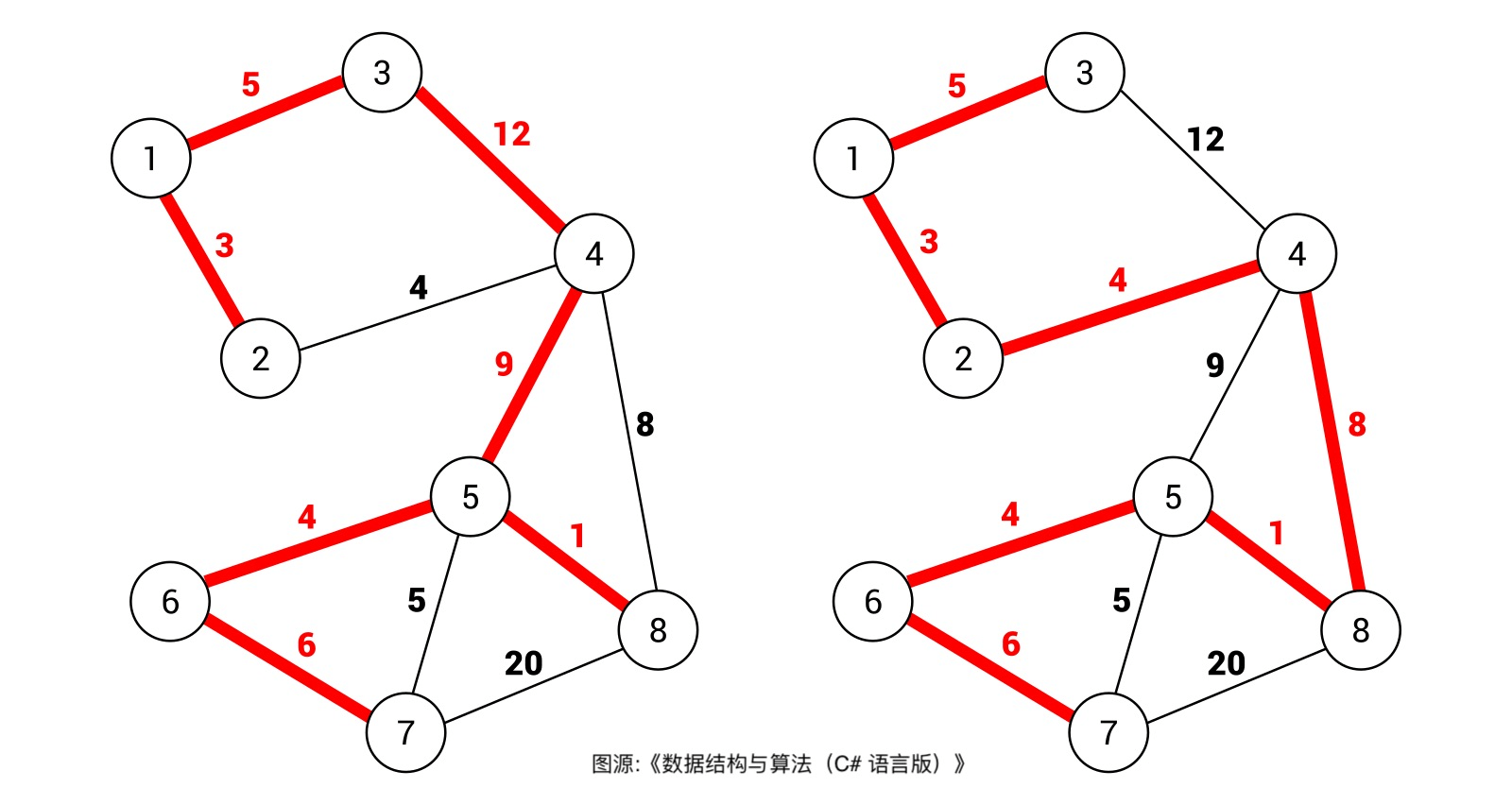
For weighted graphs, each edge has a weight, so each spanning tree has a weight sum. For example, in the figure above, the weight sum of the spanning tree on the right is obviously smaller than that of the spanning tree on the left.
Then the minimum spanning tree is well understood. Among all possible spanning trees, the spanning tree with the smallest weight is called the "minimum spanning tree".
PS: Generally speaking, we calculate the minimum spanning tree in undirected weighted graph, so in the real scene using the minimum spanning tree algorithm, the edge weight of graph generally represents scalars such as cost and distance.
Here, we need to use the union find and search set algorithm to ensure that the tree is generated in the graph (no ring).
How does the parallel search algorithm do it? Let's look at this question first:
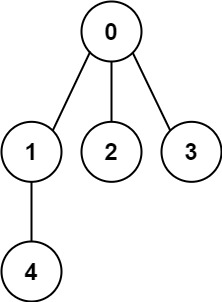
Enter n nodes numbered from 0 to n - 1 and an undirected edge list edges (each edge is represented by a node binary). Please judge whether the structure composed of these edges is a tree.

These edges form a tree and should return true:
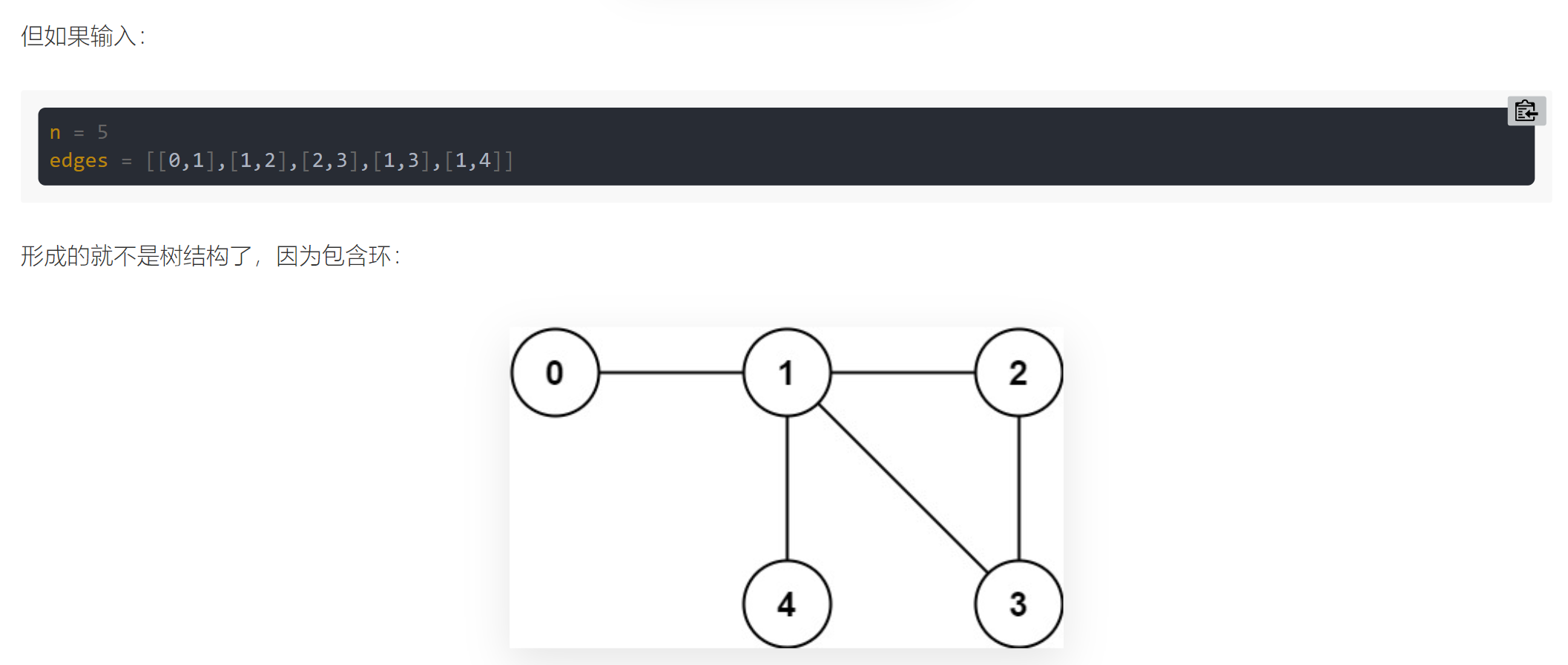
For this problem, we can think about, under what circumstances will adding an edge make the tree become a graph (ring)?
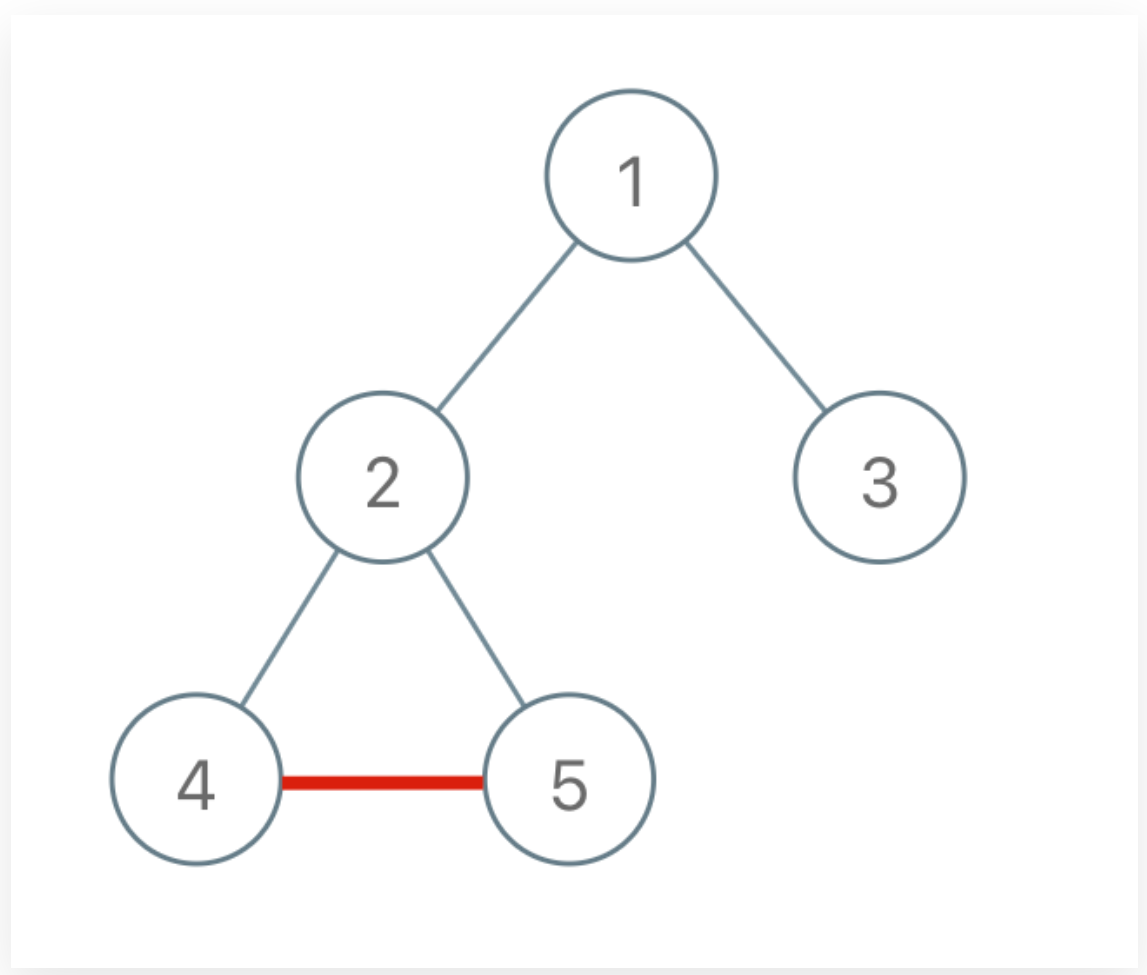
Obviously, adding an edge like this will result in a ring:
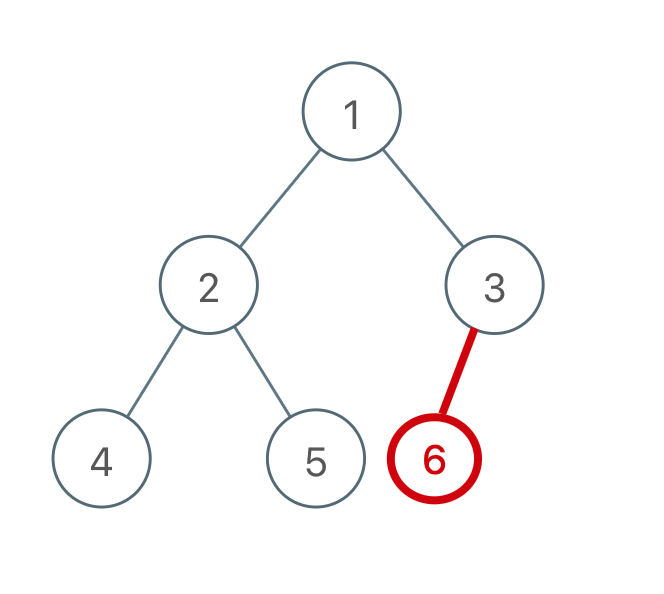
The ring will not appear if you add it as follows:
To sum up, the rule is:
For the added edge, if the two nodes of the edge are already in the same connected component, adding the edge will produce a ring; On the contrary, if the two nodes of the edge are not in the same connected component, adding this edge will not produce a ring.
Judging whether two nodes are connected (whether they are in the same connected component) is the unique skill of union find algorithm.
Parallel search set algorithm
Next, we will focus on the use and implementation of search set algorithm.
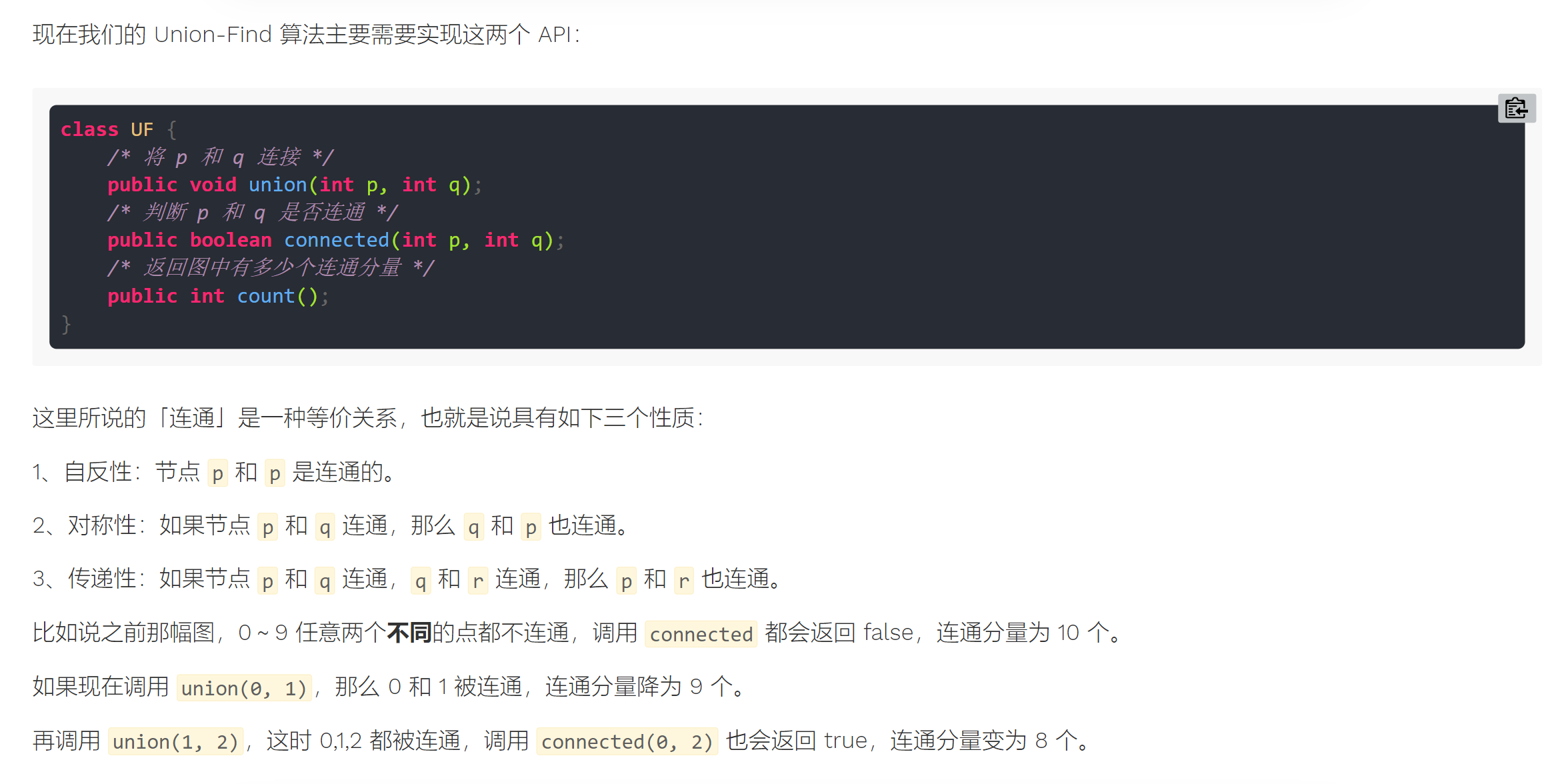
Parallel search set is mainly used to solve the problem of dynamic connectivity in graph theory.
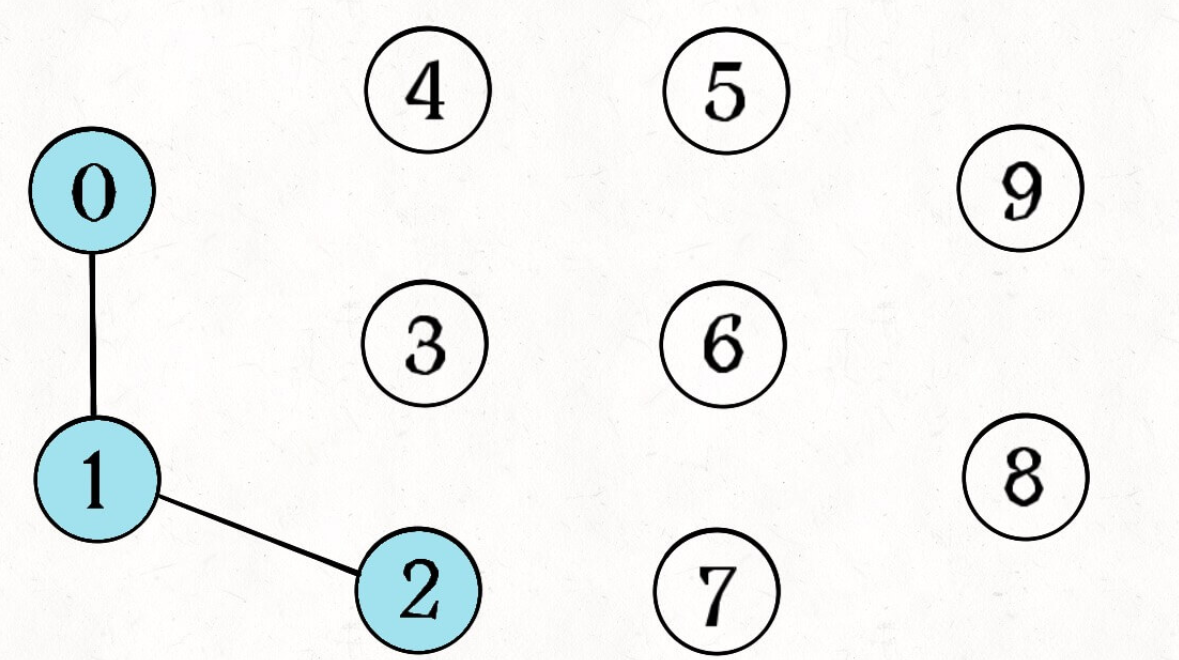
In short, dynamic connectivity can be abstracted as connecting lines to a graph. For example, in the following figure, there are 10 nodes in total. They are not connected to each other and are marked with 0 ~ 9 respectively:

class UF {
// Record connected components
private int count;
// The node of node x is parent[x]
private int[] parent;
/* Constructor, n is the total number of nodes in the graph */
public UF(int n) {
// At first, they were disconnected from each other
this.count = n;
// The parent node pointer initially points to itself (with ring)
parent = new int[n];
for (int i = 0; i < n; i++)
parent[i] = i;
}
/* Other functions */
}
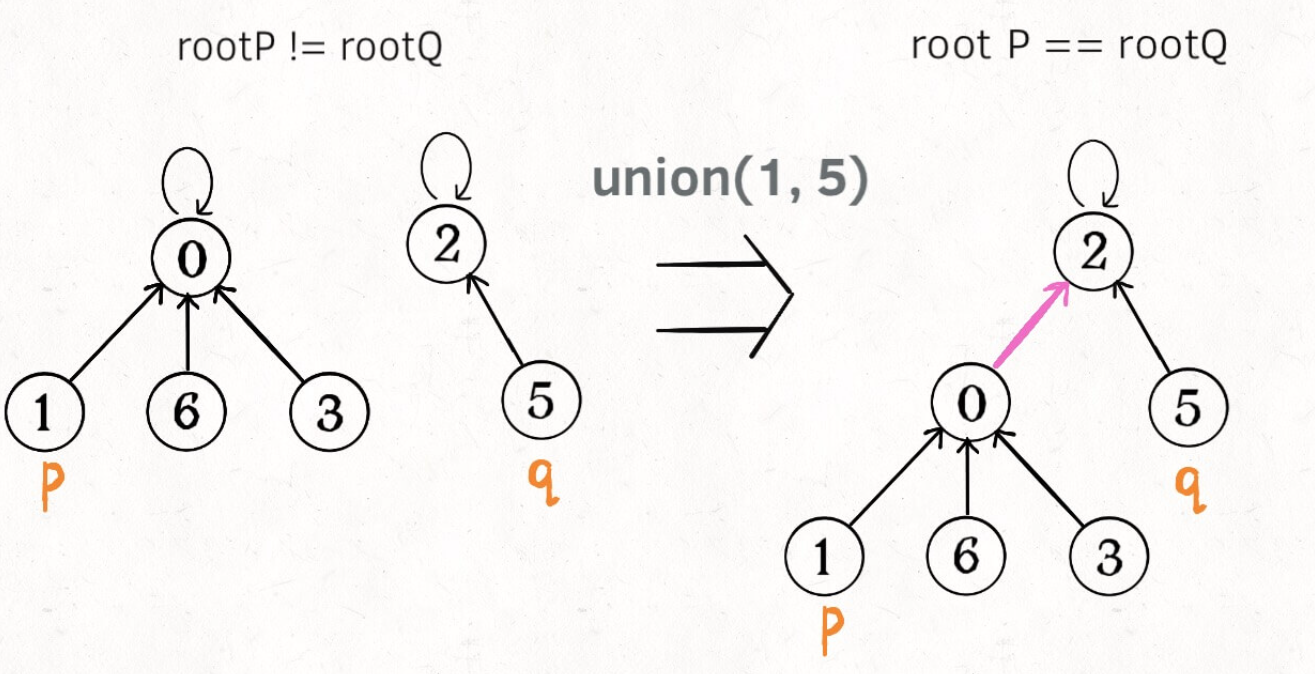
If two nodes are connected, connect the root node of one (any) node to the root node of the other node:
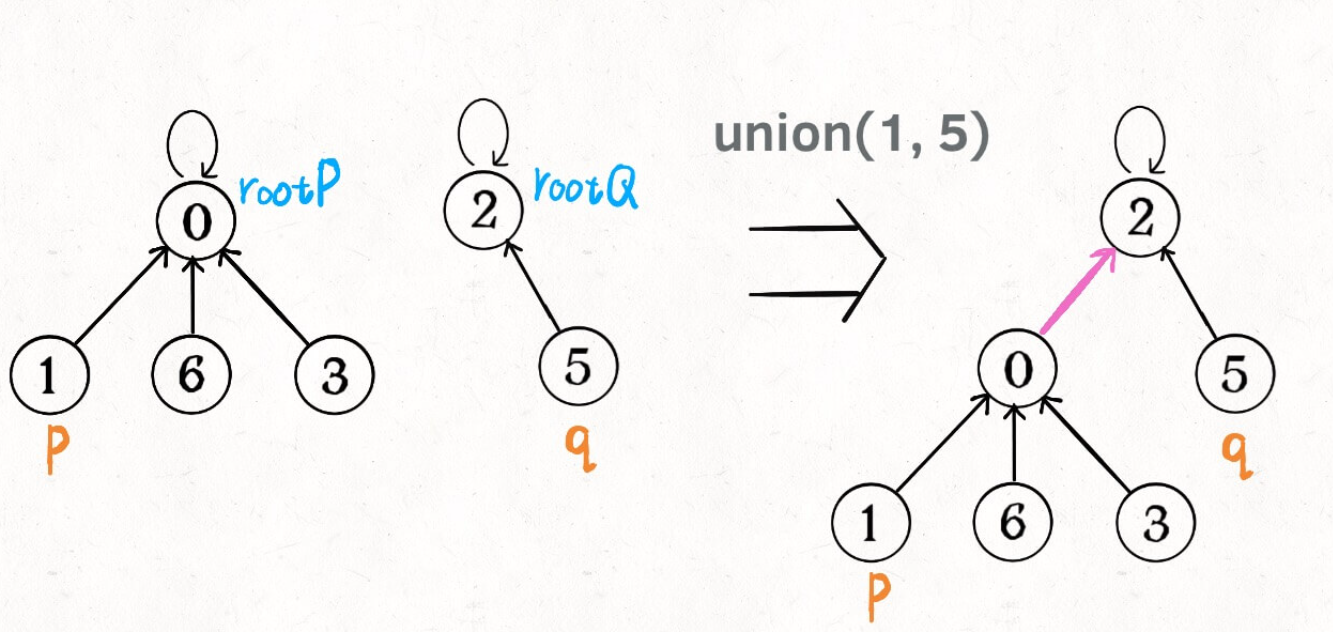
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// Merge two trees into one
parent[rootP] = rootQ;
// Parent [rootq] = so is rootp
count--; // The two components are combined into one
}
/* Returns the root node of a node x */
private int find(int x) {
// Parent of root node [x] = = x
while (parent[x] != x)
x = parent[x];
return x;
}
/* Returns the current number of connected components */
public int count() {
return count;
}
In this way, if nodes p and q are connected, they must have the same root node:
The above sentence is particularly critical. They must have the same root node!
// Judge whether the P and Q nodes are connected
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
So far, the union find algorithm has been basically completed. Isn't it amazing? We can use the array to simulate a forest, so skillfully solve this complex problem!
So what is the complexity of this algorithm? We found that the complexity of the main APIs connected and union is caused by the find function, so their complexity is the same as that of find.
The main function of find is to traverse upward from a node to the tree root, and its time complexity is the height of the tree. We may habitually think that the height of a tree is logN, but this is not necessarily true. The height of logN only exists in balanced binary trees. For general trees, there may be extreme imbalance, which makes the "tree" almost degenerate into a "linked list", and the height of the tree may become N in the worst case.
Therefore, the time complexity of the above solutions, find, union and connected, is O(N). This complexity is not ideal. What you want graph theory to solve is the problem of huge data scale such as social networks. The calls to union and connected are very frequent, and the linear time required for each call is completely unbearable.
Balance optimization
We need to know under which circumstances imbalance may occur. The key lies in the union process:
public void union(int p, int q) {
// If the header nodes are the same, there is no need to merge
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// Merge two trees into one
parent[rootP] = rootQ;
// parent[rootQ] = rootP is also OK
// Which option should we choose?
// Connected component--
count--;
At the beginning, we simply and rudely connect the tree where p is located to the root node of the tree where q is located. Then there may be a "top heavy" imbalance, such as the following situation:
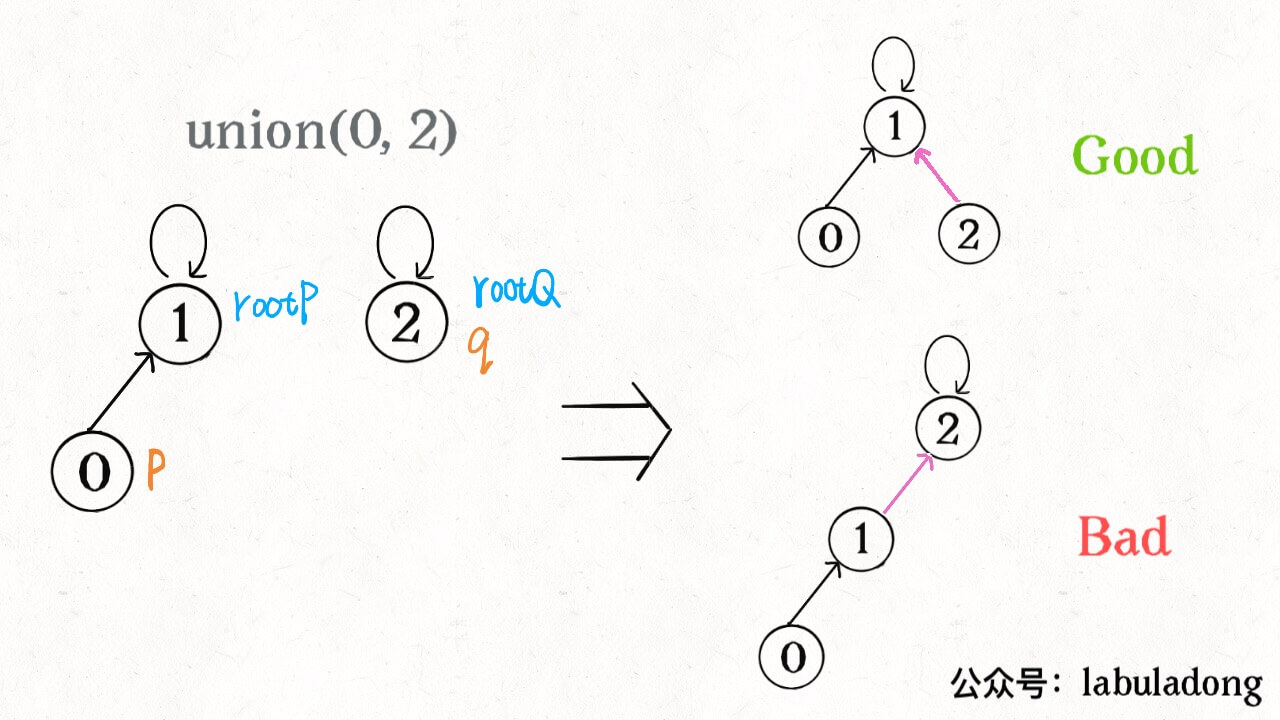
In the long run, trees may grow very unevenly. In fact, we hope that the smaller trees will be connected to the larger trees, so that we can avoid top heavy and more balanced. The solution is to use an additional size array to record the number of nodes contained in each tree. We might as well call it "weight":
class UF {
private int count;
private int[] parent;
// Add a "weight" of the array record tree
private int[] size;
public UF(int n) {
this.count = n;
parent = new int[n];
// Initially, each tree had only one node
// Weight should initialize 1
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
/* Other functions */
}
For example, size[3] = 5 means that the tree with node 3 as the root has a total of 5 nodes. In this way, we can modify the union method: the key is to have the node judgment of the tree to make the generation of the tree more balanced.
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// The small tree is connected under the big tree, which is more balanced
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
In this way, by comparing the weight of the tree, we can ensure that the growth of the tree is relatively balanced, and the height of the tree is roughly in the order of logN, which greatly improves the execution efficiency.
At this time, the time complexity of find, union and connected is reduced to O(logN). Even if the data scale is hundreds of millions, the time required is very small.
Path compression
This step of optimization is particularly simple, so it is very clever. Can we further compress the height of each tree so that the tree height remains constant?
In this way, find can find the root node of a node in O(1) time. Accordingly, the complexity of connected and union is reduced to O(1).
To do this, it's very simple. Just add one line of code to find:
private int find(int x) {
while (parent[x] != x) {
// Path compression
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
Note that the stop condition of the while loop is parent [x]= x. This is because the root node is looped. Once parent[x] == x appears, it indicates that it has reached the root node.
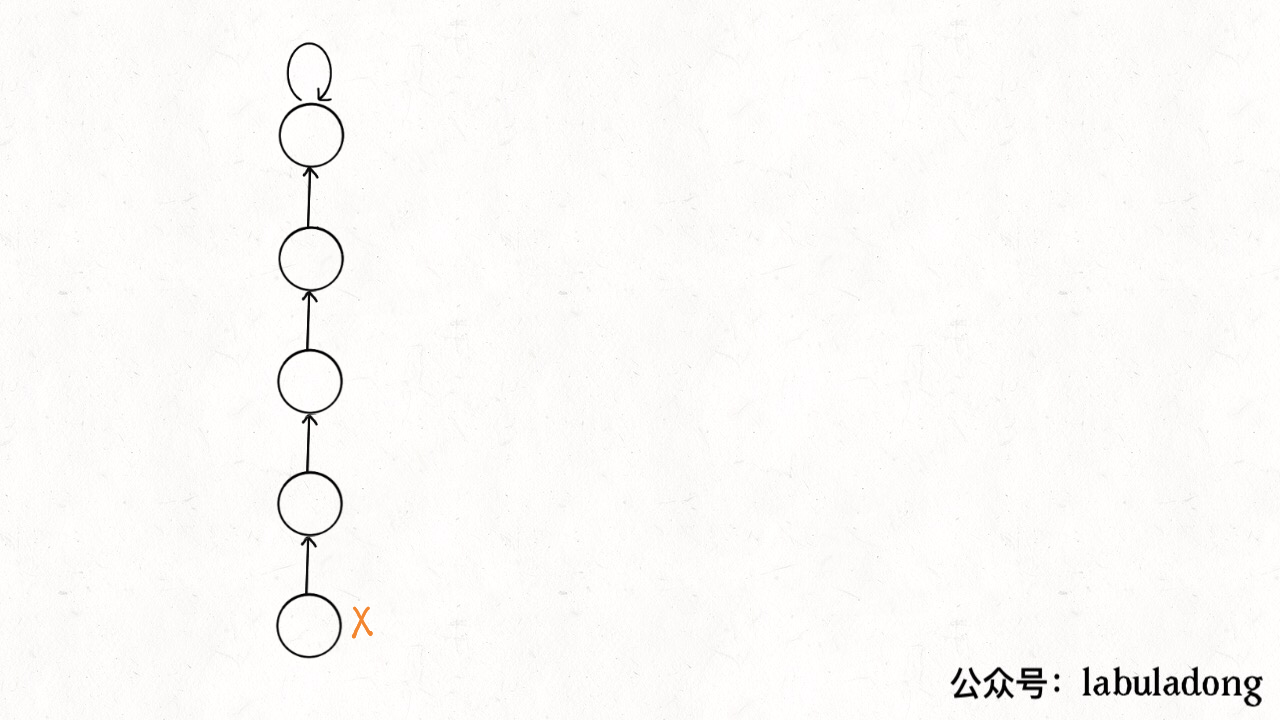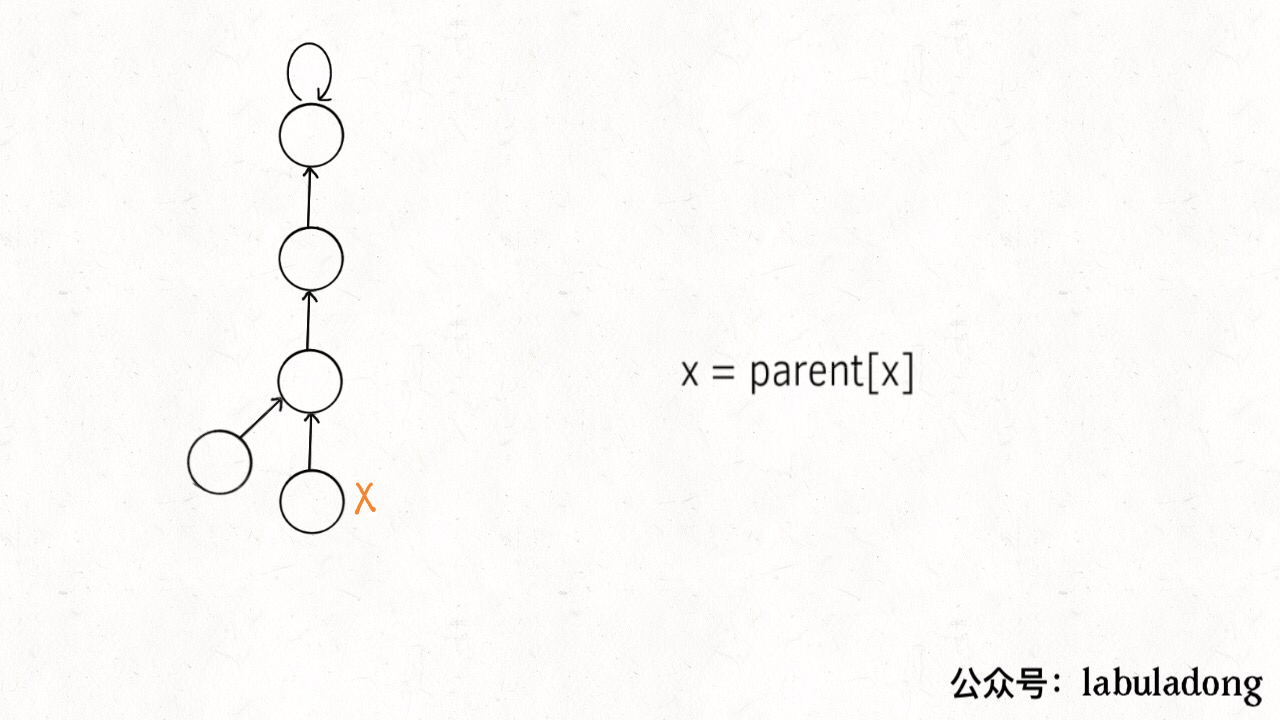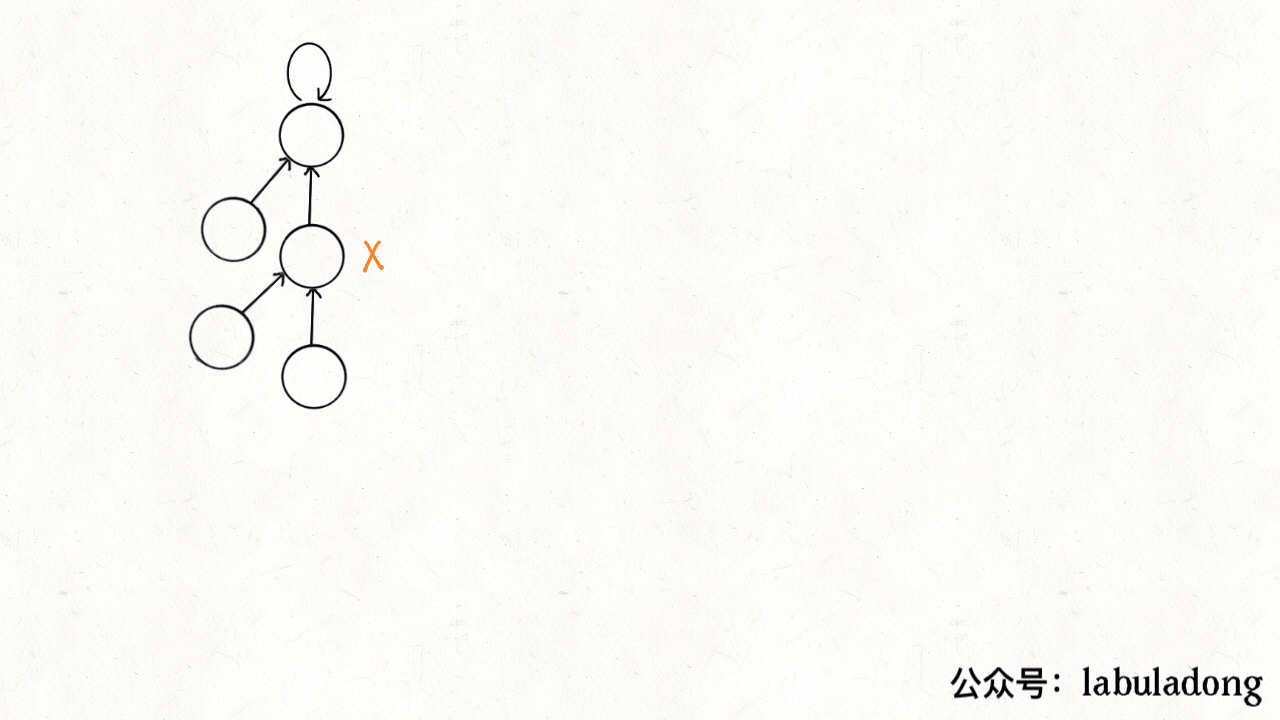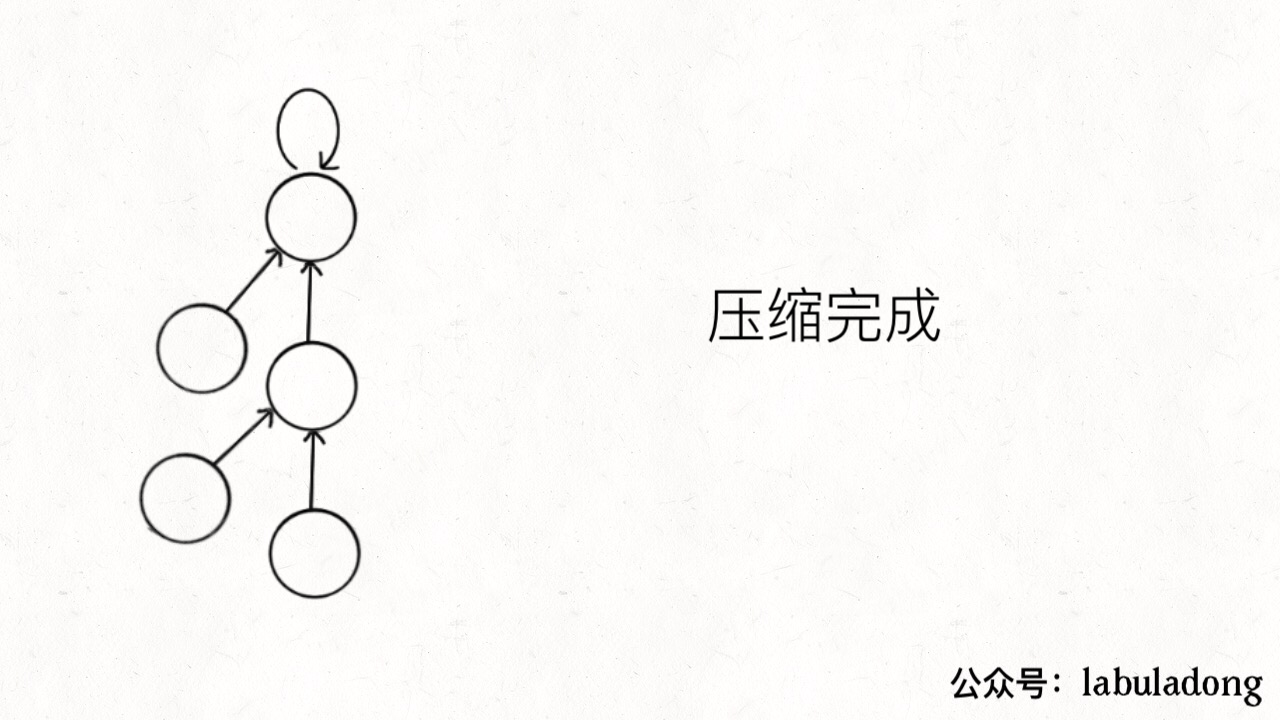
It can be seen that each time the find function is called to traverse the tree root, the tree height is conveniently shortened, and finally all tree heights will not exceed 3 (the tree height may reach 3 in union).
The purpose of path compression: find the root node faster. Anyway, the ultimate goal is to find the root node. Then I directly point the parent node of the current node to the root node, which will directly save time.
With path compression, the union function does not need to judge small trees and big trees, which has little impact on the efficiency of time. Of course, it is better to judge.
Code of overall query set:
class UF {
// Number of connected components
int count;
// Stores the root node of a tree
int[] parent;
// Record the "weight" (number of nodes) of the tree
int[] size;
// n is the number of nodes in the graph
public UF(int n) {
// Not connected at first, connected component = n
this.count = n;
parent = new int[n];
size = new int[n];
for (int i = 0; i < n; i++) {
// The node points to itself
parent[i] = i;
// Currently, this tree has only one node (root node)
size[i] = 1;
}
}
// Returns the root node of the connected component of node x
public int find(int x) {
while (parent[x] != x) {
// Path compression
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
// Connect nodes p and q
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
// Already connected: the root node is the same
if (rootP == rootQ) {
return;
}
// The small tree is more balanced when connected to the big tree
// The root node of the big tree is the root node of the whole
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
// Two connected components are combined into one connected component
count--;
}
// Judge whether nodes p and q are connected
// The essence is to find whether the root node is the same
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
// Returns the number of connected components in a graph
public int count() {
return count;
}
}