For Tribal Members Only
Introduction to Tarjan algorithm
The Tarjan algorithm is based on a depth-first search algorithm that defines the order number (timestamp) of the nodes where DFN(u) is the node and the order number of the earliest node that a subtree with Low(u) is the u or u can trace back to
C++ code, using a chain forward star map
#include<bits/stdc++.h>
using namespace std;
struct node{
int to, nxt;
}e[M];
int n, m, hd[N], dfn[N], low[N], cnt, tot;
void add(int u, int v){
e[++cnt].to = v;
e[cnt].nxt = hd[u];
hd[u] = cnt;
}
void tarjan(int u){
dfn[u] = low[u] = ++tot;
for(int j = hd[u]; j; j = e[j].nxt){
int v = e[j].to; // v is a child node of u
if(!dfn[v]){
tarjan(v);
if(low[u] > low[v]) low[u] = low[v];
}else{
//It's important to note here that some of the code is written as downline comments
//This method of writing will make mistakes when calculating cut points. Is there any analysis below the article???
// if(low[u] > low[v]) low[u] = low[v];
if(low[u] > dfn[v]) low[u] = dfn[v];
}
}
}
int main()
{
cin >> n >> m;
int u, v;
for(int i = 1; i <= m; i++){
scanf("%d%d", &u, &v);
add(u, v);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
return 0;
}
Tarjan cut point
In an undirected connected graph, if one of the points and all the edges connecting the points are removed, the graph is no longer connected, and this point is called a secant point.
How to Use Tarjan to Find Cutting Points
case1: son of dfn[x] <= low[x] not root node
For edges (u, v), if dfn[u]<=low[v], that is, V is the earliest point that its subtree can go back to, and it can only be u at the earliest time. To get to u, the back edge of u or the parent-child edge of u are needed. That is to say, if u is removed, the back edge of u and the parent-child edge of u will disappear, then the earliest point that V can trace back to is behind u and cannot reach the vertex before u, where u is the cut point.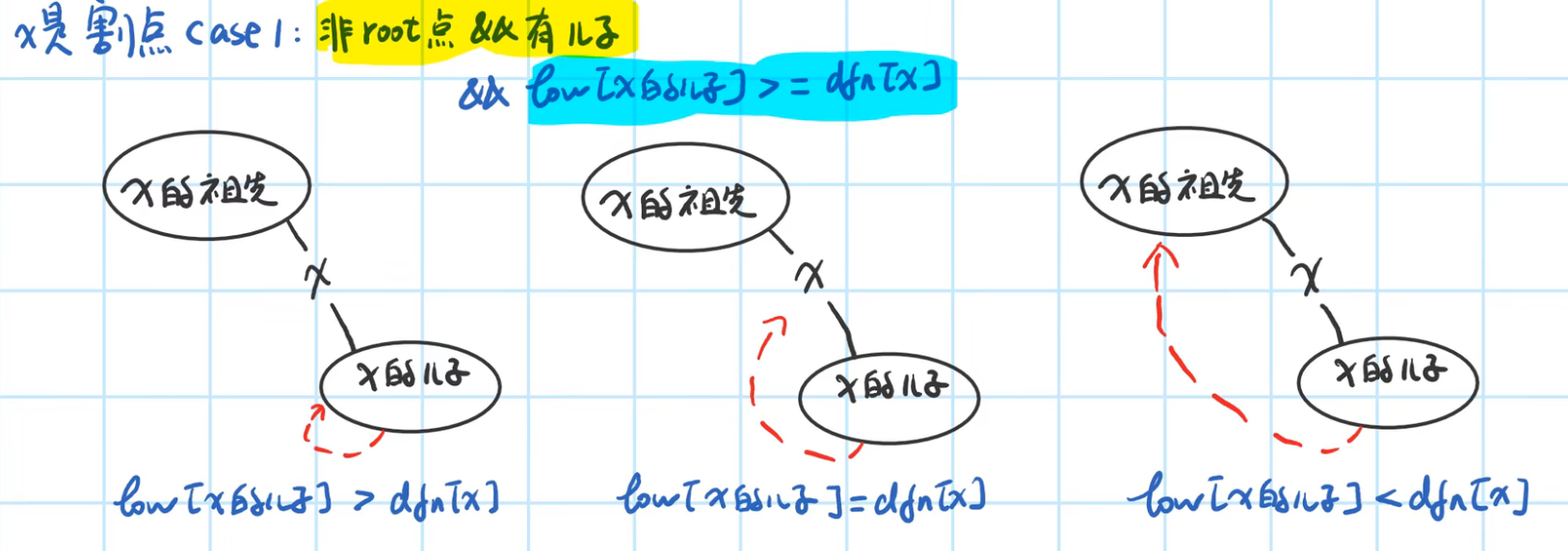
case2:root node number of sons >=2
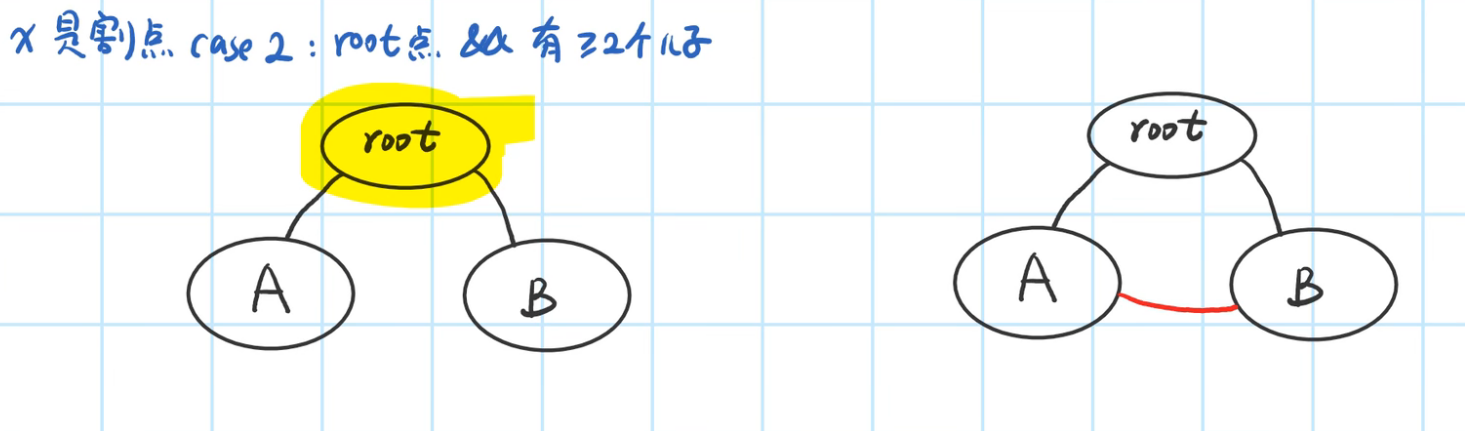
Explain the graph on the right here, because there is a path connection between A and B, so the order of dfs is root->A->B, so root has only one son, root is not a cut point
Why should root be considered separately? In the following figure, Tarjan runs and all points have a low of 1
low[root] == dfn[root], satisfies case1, but root is obviously not a cut point, so it needs to be considered separately

Detailed Code
#include<bits/stdc++.h>
using namespace std;
const int N = 20001, M = 100001;
int n, m, hd[N], cnt;
int dfn[N], low[N], tot, num;
bool iscut[N];
struct node{
int to, nxt;
}e[M * 2]; // Note that because it is an undirected graph, the number of edges is M*2
void add(int u, int v){
e[++cnt].to = v;
e[cnt].nxt = hd[u];
hd[u] = cnt;
}
void tarjan(int root, int u){
dfn[u] = low[u] = ++tot;
int child = 0;
for(int j = hd[u]; j; j = e[j].nxt){
int v = e[j].to;
if(!dfn[v]){
tarjan(root, v);
low[u] = min(low[u], low[v]);
if(root == u) child++;
//You can't count the number of cut points here, it will repeat, dfn[u] <= low[v1], dfn[u] <= low[v2].....
//The u-point is repeated many times
if((root == u && child > 1) || (root != u && dfn[u] <= low[v]))
iscut[u] = true;
}
//This must be dfn[v], not low[v] as illustrated below
else low[u] = min(low[u], dfn[v]);
}
}
int main()
{
cin >> n >> m;
int x, y;
for(int i = 1; i <= m; i++)
scanf("%d %d", &x, &y), add(x, y), add(y, x);
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i, i);
for(int i = 1; i <= n; i++)
if(iscut[i]) num++;
cout << num << endl;
for(int i = 1; i <= n; i++)
if(iscut[i]) cout << i << " ";
return 0;
}
Note explaining why can't low[u] = min(low[u], low[v])

Cutting Point Template Title
Video detailing of the messy Big Brother 233 in station b
Tarjan's Cutting Edge (Bridge)
In an undirected connected graph, if one of the edges is deleted, the graph is no longer connected, and this edge is called a secant edge.
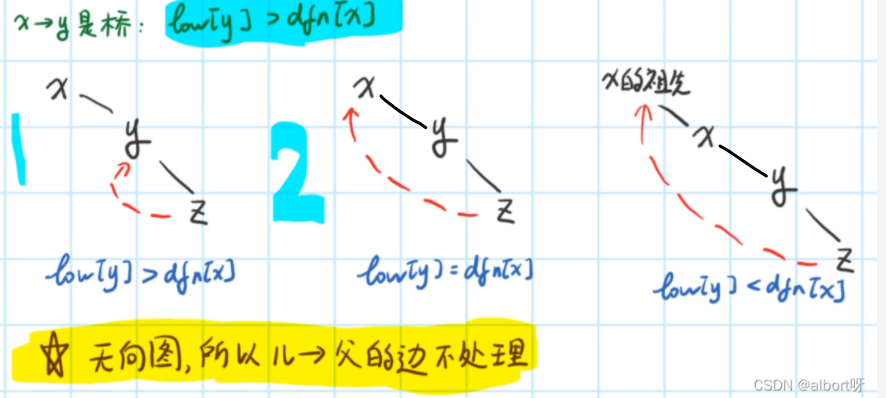
Cut Edge Note that undirected graph edges can only be parent->child, not child->father, otherwise
Under the action of low[u] = min(low[u], dfn[v]), any DFN [parent] >= low[child]
When we use the chain forward star storage edge, the edge number starts from 2, so the two-way edge numbers of the undirected graph are x and x^1. The function of ^1 is to add 1 to even numbers and subtract 1 from odd numbers.
#include<bits/stdc++.h>
using namespace std;
const int N = 20001, M = 100001;
int n, m, hd[N], cnt;
int dfn[N], low[N], tot, num;
bool iscut[N];
struct node{
int to, nxt;
}e[M * 2]; // Note that because it is an undirected graph, the number of edges is M*2
void add(int u, int v){
e[++cnt].to = v;
e[cnt].nxt = hd[u];
hd[u] = cnt;
}
void tarjan(int u, int eid){
dfn[u] = low[u] = ++tot;
for(int j = hd[u]; j; j = e[j].nxt){
int v = e[j].to;
if(!dfn[v]){
tarjan(root, v);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u])
bridge[i] = bridge[i ^ 1] = true;
}
//Guarantee not to point to parent node
else if(i != (eid ^ 1))low[u] = min(low[u], dfn[v]);
}
}
int main()
{
cin >> n >> m;
int x, y;
cnt = 1;
for(int i = 1; i <= m; i++)
scanf("%d %d", &x, &y), add(x, y), add(y, x);
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i, 0);
for (int i = 2; i < cnt; i += 2)
if (bridge[i])
printf("%d %d\n", e[i ^ 1].to, e[i].to);
return 0;
}
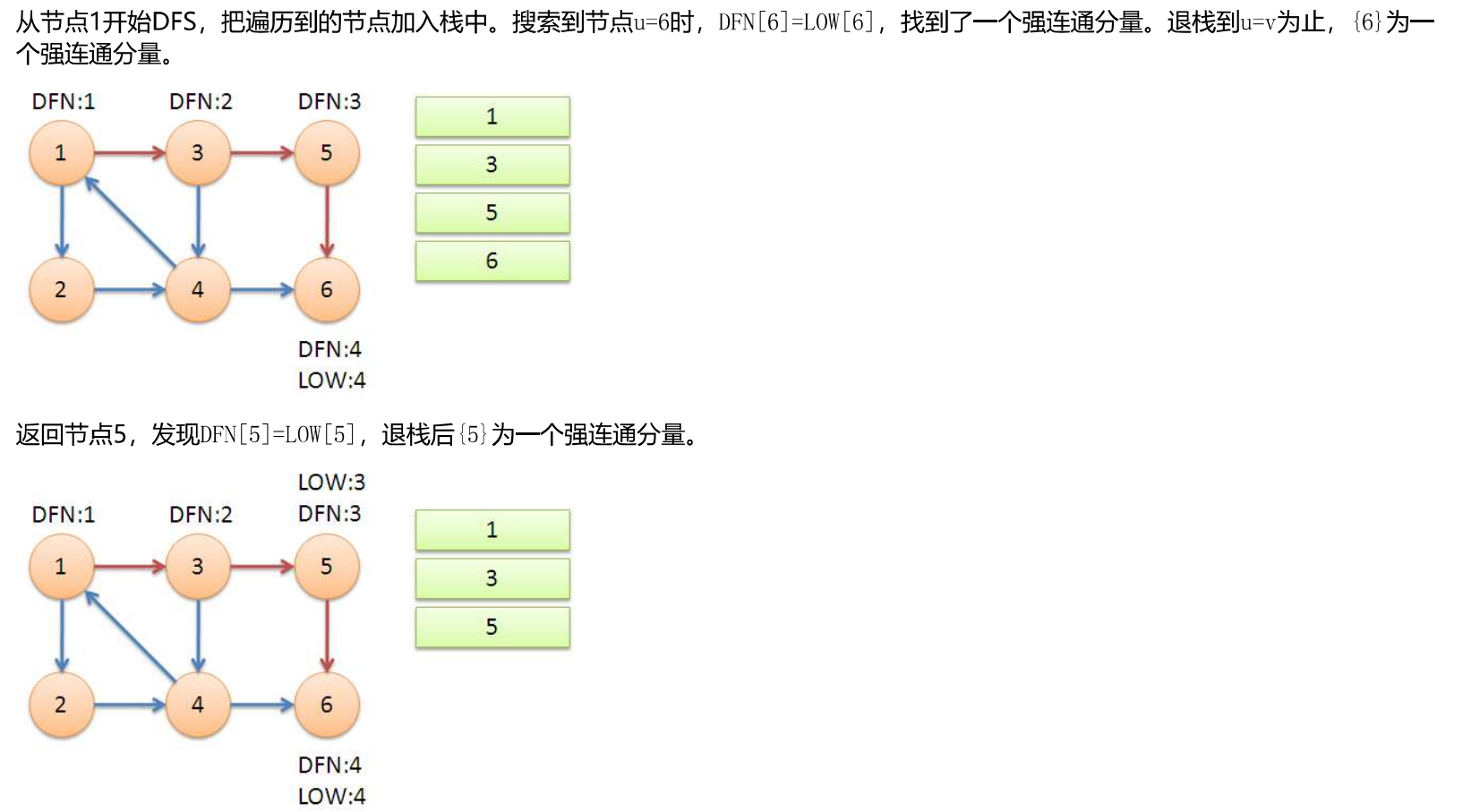
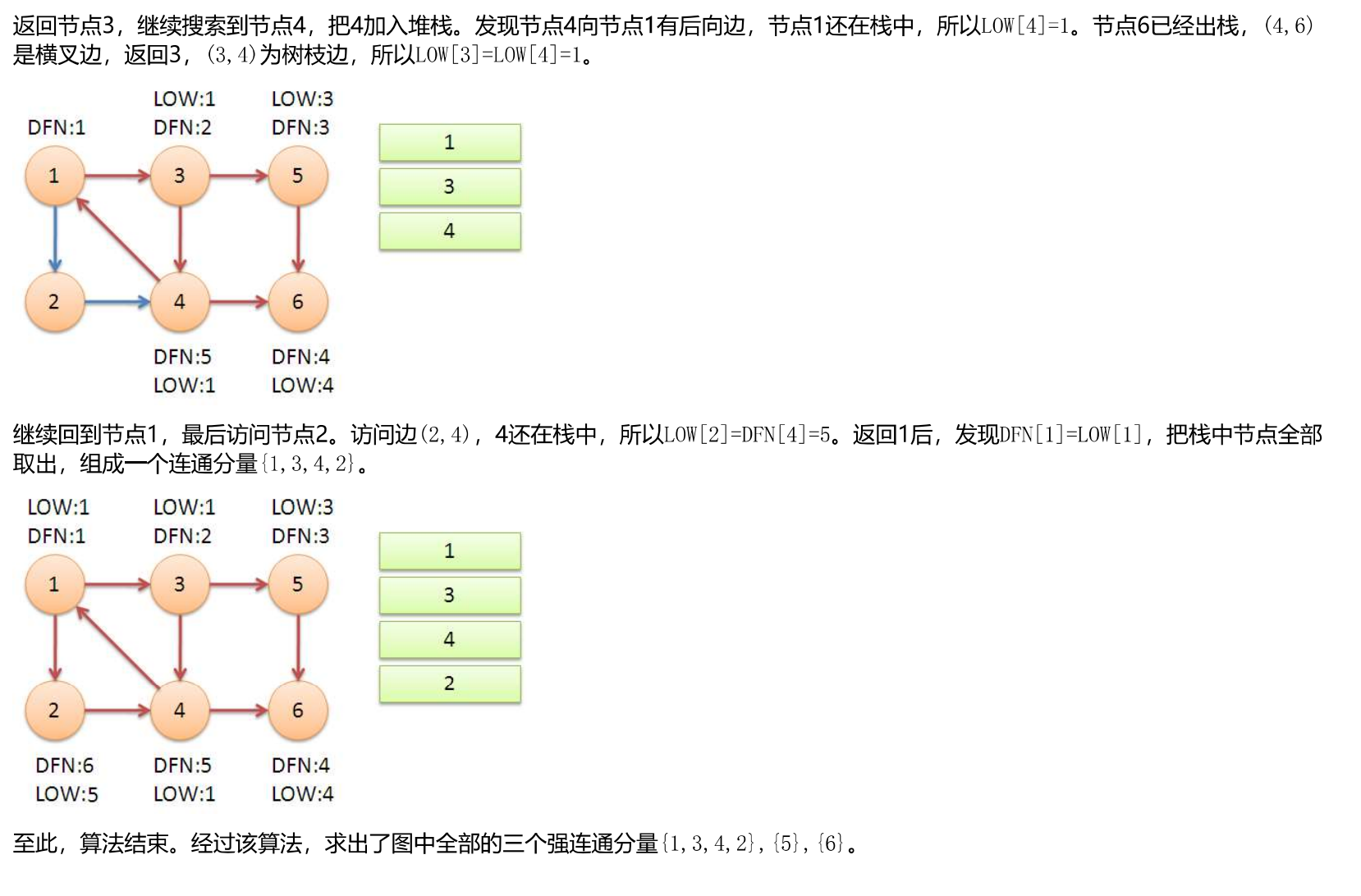
Tarjan Strongly Connected Component
Strong connectivity: Directed graph, any two-way communication
Strong Connected Component: A strongly connected subgraph of a directed graph, the concept of which is a directed graph divided into many parts, each part can reach each other inside, but different parts cannot reach each other or can only be reached in one direction.
Specific code
#include<bits/stdc++.h>
using namespace std;
const int N = 20001, M = 100001;
int n, m, hd[N], cnt;
int dfn[N], low[N], S[N], beLong[N], top, tot, scNum;
bool inStack[N];
struct node{
int to, nxt;
}e[M * 2]; // Note that because it is an undirected graph, the number of edges is M*2
void add(int u, int v){
e[++cnt].to = v;
e[cnt].nxt = hd[u];
hd[u] = cnt;
}
//Add a new stack, inStack[], a stack top subscript top
//A new tag array beLong[] is added to record which strong connected component each vertex belongs to, and the label of the strong connected component scNum
void tarjan(int u){
dfn[u] = low[u] = ++tot;
inStack[u] = true; //Mark u point is already on the stack
S[++top] = u;
for(int j = hd[u]; j; j = e[j].nxt){
int v = e[j].to;
if(!dfn[v]){
tarjan(v);
low[u] = min(low[u], low[v]);
}
//Points in a well-established strongly connected component cannot update the current point
//Avoid one-way edges between two strongly connected components, as shown in the following figure
else if(inStack[v])low[u] = min(low[u], dfn[v]);
}
//When all descendant nodes of u have finished searching
if(dfn[u] == low[u]){
//The label of the strong connectivity strongly connected component
scNum++;
int v;
do{
v = S[top--];
inStack[v] = false;
beLong[v] = scNum;
}while(v != u);
}
}
int main()
{
cin >> n >> m;
int x, y;
cnt = 1;
for(int i = 1; i <= m; i++)
// One-way Edge
scanf("%d %d", &x, &y), add(x, y);
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
for(int i = 1; i <= n; i++)
cout << beLong[i] << " ";
return 0;
}
else if(inStack[v])low[u] = min(low[u], dfn[v]), if no limitation of inStack[v], the following will occur,
The dfn and low of all points after dfs are 1, resulting in the strong connectivity component composed of 3,4 points not found
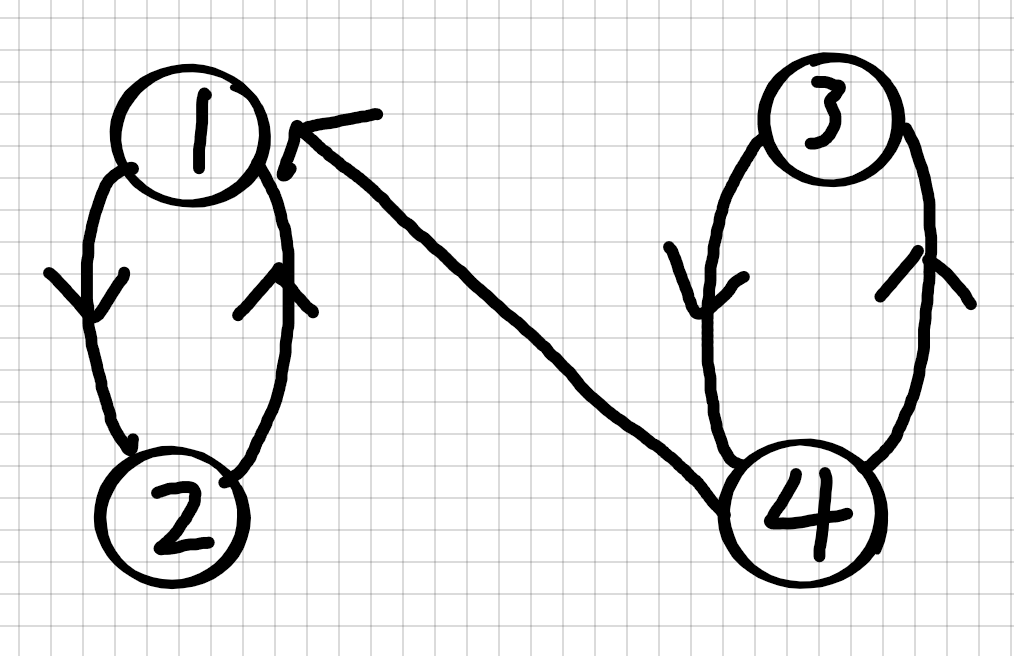
Reference to Lough Valley

Biconnected component
Tarjan Edge-finding Double (E-BCC)
An undirected connected graph without a cut edge (bridge) is called an edge double connected graph
In undirected graph, if u and v cannot be disconnected by deleting that edge, then u and v edges are double connected
That is, the path from u to v does not have to go by an edge
Solution: Tarjan finds the cutting edge, marks the cutting edge, and dyes it once with dfs (no cutting edge is used)
Trajan Cutting Edge
void dfs(int u)
{
beLong[u] = eNum;//dyeing
for(int j = hd[u]; j; j = e[j].nxt){
{
int v = e[j].to;
if (bridge[j]) // Skip Cutting Edge
continue;
if(!beLong[v]) dfs(v);
}
}
for(int i = 1; i <= n; i++){
if(!beLong[i]) dfs(i);
}
P4214 [CERC2015]Juice Junctions
P2860 [USACO06JAN]Redundant Paths G
Tarjan Point Double (V-BCC)
In undirected graphs, if the deletion of that point (non-u-point and v-point) does not disconnect u and v, then u and V points are dual connected
That is, the path from u to V does not have to go through a point (except u,v)
Note: A graph with two points and one edge is also a BCC
Secant points in undirected connected graphs must belong to at least two BCCs, and non-secant points must belong to only one BCC
The cut points will belong to at least two BCCs even if they are adjacent. The intersections between BCCs are cut points, so non-cut points belong to only one BCC
Solution:
The node is stacked up to a node. If the low value of the target node is not less than the dfn value of the current node, the node is stacked up to the target node (the target node is stacked out), the stack node and the current node are stored in the BCC. For each BCC, the first point it finds in the DFS tree must be the cutting point or the tree root of the DFS tree.
It is proved that the cut point is the intersection point between BCCs, so the cut point is at the edge of the BCC, and the BCC is connected by the cut point, so the first point that BCC is found in the DFS tree is the cut point. The special case is that for the BCC to which the starting point of DFS belongs, the first point discovered is the tree root of the DFS tree
The above result is equivalent to each BCC being in a subtree of its first discovered point (a cut point or tree root)
This way, whenever a BCC is found (low[v]>=dfn[u]), the subtree is stacked and the subtree and the current node (cut point or root) are added to the BCC.
#include<bits/stdc++.h>
using namespace std;
const int N = 20001, M = 100001;
int n, m, hd[N], cnt;
int dfn[N], low[N], S[N], top, tot, bNum;
vector <int> bcc [N];
struct node{
int to, nxt;
}e[M * 2]; // Note that because it is an undirected graph, the number of edges is M*2
void add(int u, int v){
e[++cnt].to = v;
e[cnt].nxt = hd[u];
hd[u] = cnt;
}
//Added BCC variable array vector <int>bcc[N];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
S[++top] = u;
for(int j = hd[u]; j; j = e[j].nxt){
int v = e[j].to;
if(!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]){ //u is a cut point or root
bNum++;
int v;
do{
v = S[top--];
bcc[bNum].push_back(v);
}while(u != v);
//The cut point belongs to the dual component of multiple points, so the cut point should be put back
S[++top] = v;
//When can a cut point come out of the stack, only when traversing to another cut point
}
} else {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
cin >> n >> m;
int x, y;
cnt = 1;
for(int i = 1; i <= m; i++)
// One-way Edge
scanf("%d %d", &x, &y), add(x, y), add(y, x);
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
for(int i = 1; i <= bNum; i++){
for(int j = 0; j < bcc[i].size(); j++)
cout << bcc[i][j] << " ";
cout << endl;
}
return 0;
}
A point double-connected graph can be solved without crossing a secant point in dfs
SP2878 KNIGHTS - Knights of the Round Table
P3225 [HNOI2012] Mine Setup
P5058 [ZJOI2004] sniffer
Tarjan Indentation
That is, all strongly connected components derived by tarjan become points (collections or sharing some information), so directed rings become directed acyclic graphs (DAGs)
#include<bits/stdc++.h>
using namespace std;
const int N = 20001, M = 100001;
int n, m, hd[N], cnt;
int a[N], dfn[N], low[N], S[N], beLong[N], top, tot;
bool inStack[N], exist[N];
struct node{
int u, to, nxt;
}e[M * 2]; // Note that because it is an undirected graph, the number of edges is M*2
void add(int u, int v){
e[++cnt].to = v;
e[cnt].u = u;
e[cnt].nxt = hd[u];
hd[u] = cnt;
}
//Add a new stack, inStack[], a stack top subscript top
//A new tag array beLong[] is added to record which strong connected component each vertex belongs to, and the label of the strong connected component scNum
void tarjan(int u){
dfn[u] = low[u] = ++tot;
inStack[u] = true; //Mark u point is already on the stack
S[++top] = u;
for(int j = hd[u]; j; j = e[j].nxt){
int v = e[j].to;
if(!dfn[v]){
tarjan(v);
low[u] = min(low[u], low[v]);
}
//Points in a well-established strongly connected component cannot update the current point
//Avoid one-way edges between two strongly connected components, as shown in the following figure
else if(inStack[v])low[u] = min(low[u], dfn[v]);
}
//When all descendant nodes of u have finished searching
if(dfn[u] == low[u]){
//The label of the strong connectivity strongly connected component
int v;
exist[u] = true;
do{
v = S[top--];
inStack[v] = false;
beLong[v] = u;
//Merging Weights of Strongly Connected Components
a[u] += a[v];
}while(v != u);
//Finally a[u] + a[u]
a[u] /= 2;
}
}
int main()
{
cin >> n >> m;
int x, y;
cnt = 1;
for(int i = 1; i <= m; i++)
// One-way Edge
scanf("%d %d", &x, &y), add(x, y);
// Enter a weight for each point
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
//Rebuild Map
cnt = 0;
for(int j = 1; j <= m; j++){
//There will be a double edge after the indentation point, which generally has no effect
//Create a new edge if it belongs to two different indentations
if(beLong[e[j].u] != beLong[e[j].to]){
add(beLong[e[j].u], beLong[e[j].to]);
}
}
return 0;
}
Indentation Point
P2341 [USACO03FALL / HAOI2006] Popular Bovine G