At present, it is still a pure vegetable Wang 🐶. The typical kind of food is noisy 👀, I can't do a lot of things well, I can't say a lot of things well, and I can't write questions 😅, Still working, still moving forward 👣.
Because you are unique to me 💓. At the moment of opening this article, I believe that we need each other 🌹🌹
Always remember: write the algorithm carefully and share it with your heart. No negative algorithm, no mistake. Thank you for meeting (^㉨^). The ten breathing methods of the Blue Bridge Cup are the ten knowledge points selected by the author combined with his own study. In order to understand the principle of the algorithm like reading comics. When you do encounter relevant exercises in the future, you can go back and combine my problem solving report to deepen your understanding.
Do you have any impression of sister Ren's unique sun wheel knife? I feel that it's so light to dance and looks so natural and unrestrained

But it's easy to burst into tears 😭😭 That's the sacrifice in infinite city 😭😭😭
No, I have to get back to the point~
Go to the butterfly house and begin to practice the breathing method we are going to learn today - two points
💓 It is said that only 10% of programmers can write correctly
The basic usage of bisection is to find in monotone sequence or monotone function. Therefore, when the problem is monotonous, the solution can be transformed into decision through dichotomy. To be more popular, it can be understood as judging the position of the answer in this monotonous interval
(according to the complexity theory, it is less difficult to judge than to solve).
| Further, we can also expand to solve the extreme value of unimodal function and related problems by trisection method. |
| Second, the difficulty lies in the handling of details: |
For bisection in integer field, it is necessary to pay attention to the opening and closing of the termination boundary and the selection of left and right intervals, so as to avoid missing the answer or causing dead circulation;
For the dichotomy of real number field, we need to pay attention to the problem of accuracy.
🌟 Bisection on an integer set
The premise of using dichotomy is to ensure that the final answer is in a closed interval [ l , r ] [l,r] Within [l,r], cycle to l = r l = r L = end of R, the middle value of each two points m i d mid mid will belong to one of the left half and the right half.
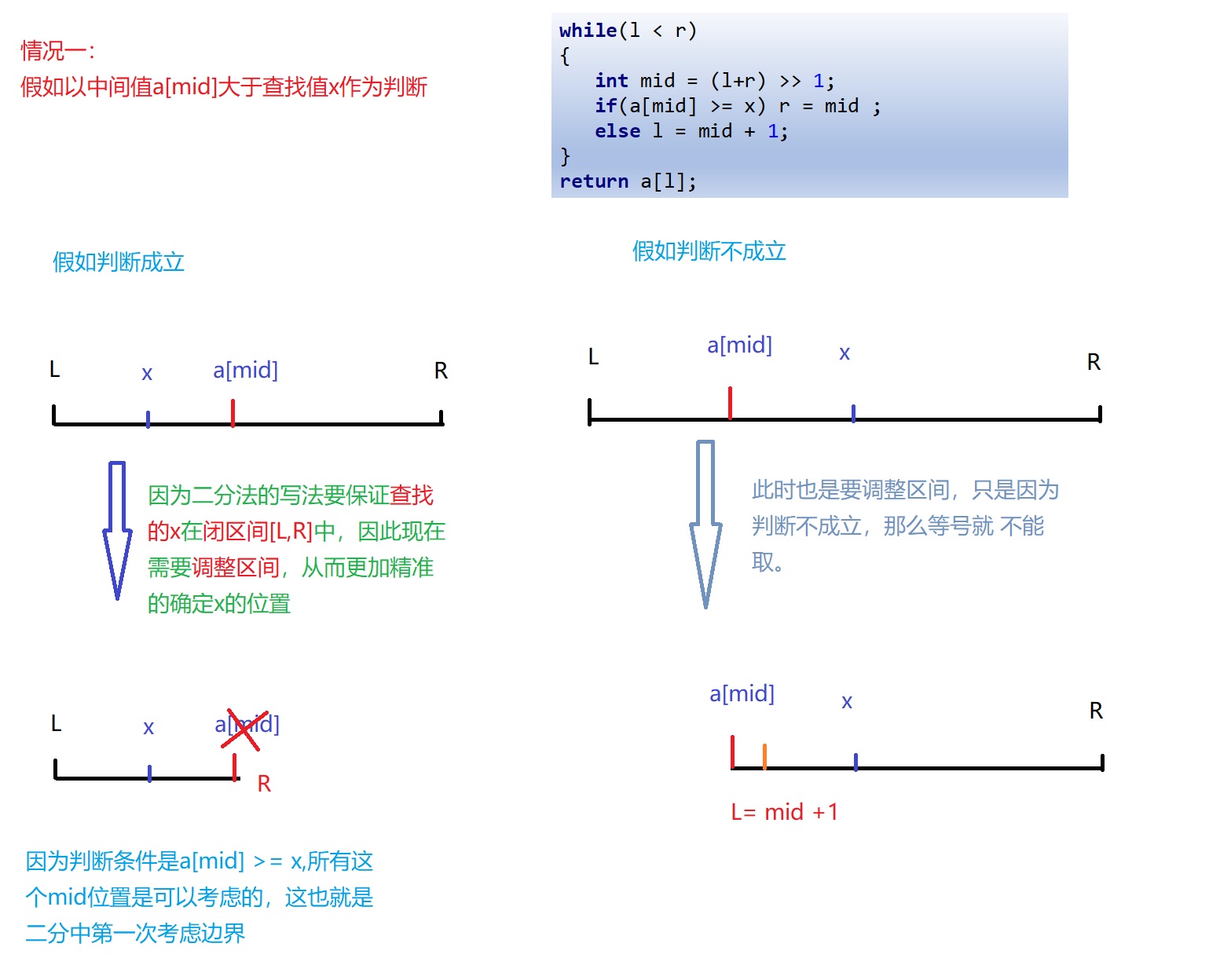
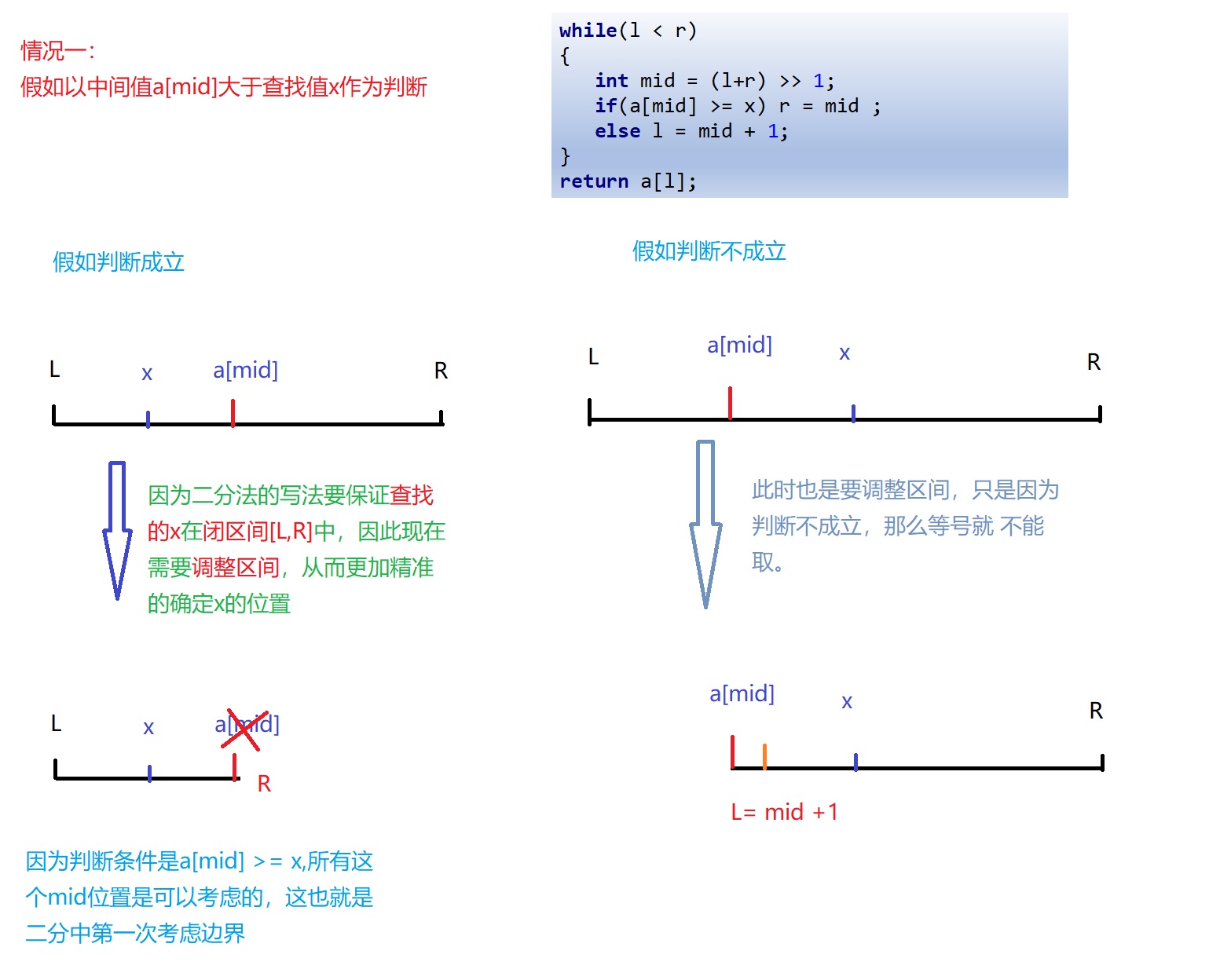
Case 1: in monotonically increasing sequence a a Find the position with the smallest number greater than or equal to x in a.
while(l < r)
{
int mid = (l+r) >> 1;
if(a[mid] >= x) r = mid ;
else l = mid + 1;
}
return a[l];
The effect of picture demonstration in case 1 is as follows:
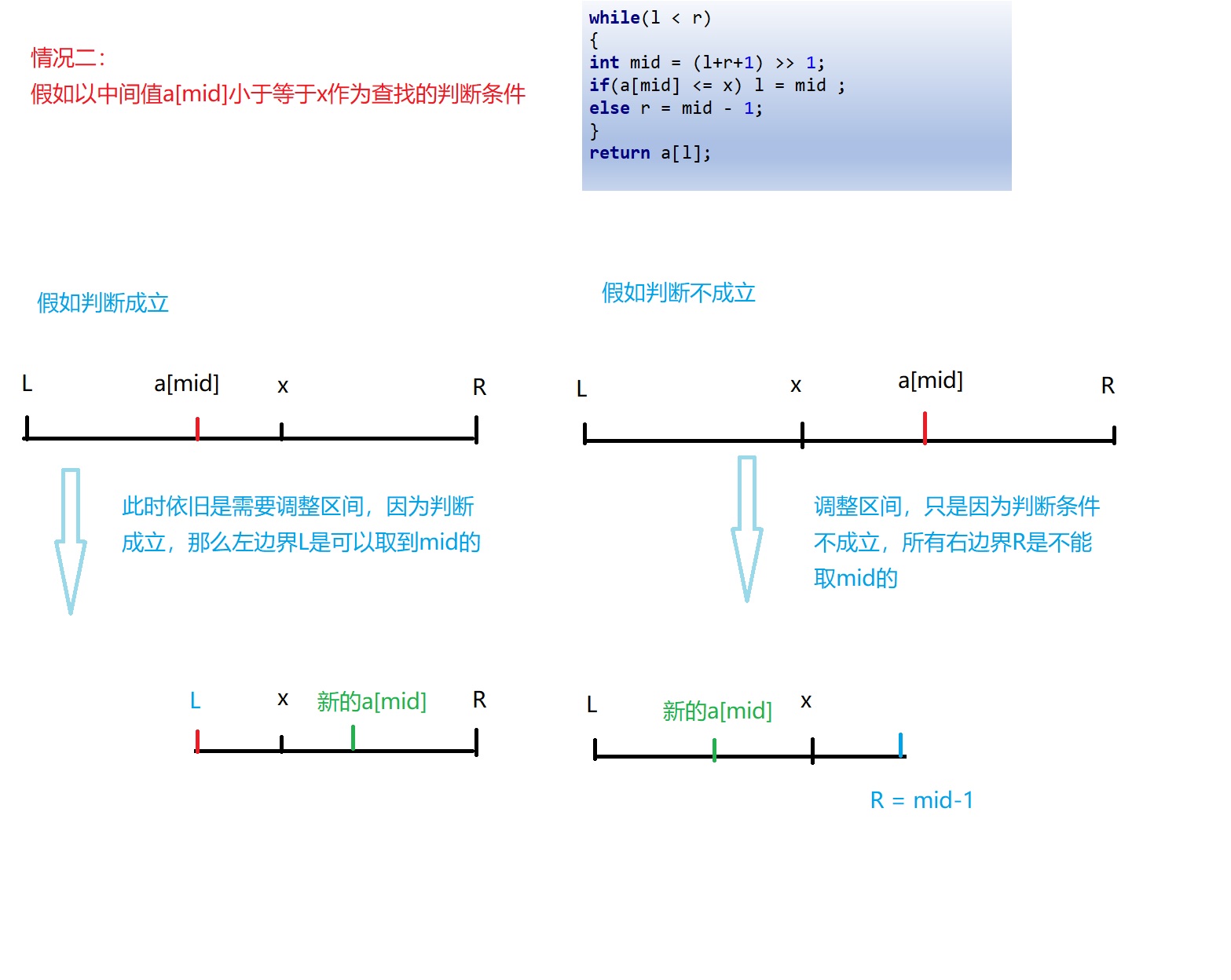
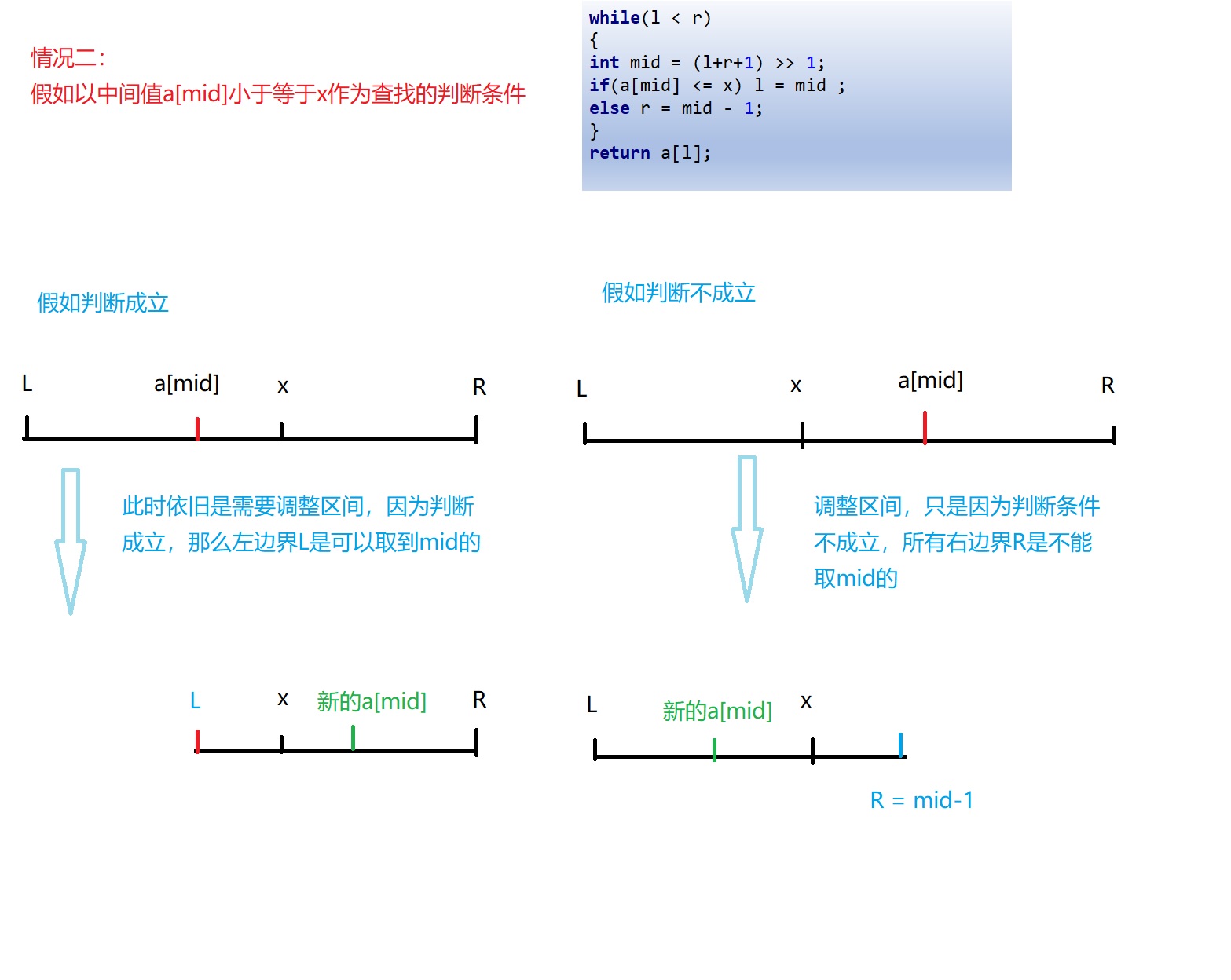
Case 2: find the largest position in the number less than or equal to x in the monotonically increasing sequence a
while(l < r)
{
int mid = (l+r+1) >> 1;
if(a[mid] <= x) l = mid ;
else r = mid - 1;
}
return a[l];
For case 2, the effect of picture demonstration is as follows:
| As shown in the above two codes, this dichotomy may take two forms: |
1. When the range is reduced,
r
=
m
i
d
r=mid
r=mid,
l
=
m
i
d
+
1
l=mid+1
l=mid+1, when the intermediate value is taken,
m
i
d
=
(
l
+
r
)
>
>
1
mid = (l+r)>>1
mid=(l+r)>>1
2. When the range is reduced,
l
=
m
i
d
l=mid
l=mid,
r
=
m
i
d
−
1
r=mid-1
r=mid − 1, when the intermediate value is taken,
m
i
d
=
(
l
+
r
+
1
)
>
>
1
mid = (l+r+1)>>1
mid=(l+r+1)>>1
Pay attention to the wording of the second paragraph, if the second paragraph is also used m i d = ( l + r ) > > 1 mid = (l+r)>>1 Mid = (L + R) > > 1, then when r − l = 1 r-l=1 When r − l=1, i.e r = l + 1 r = l+1 r=l+1, then:
m i d = ( r + l ) > > 1 mid = (r+l)>>1 mid=(r+l)>>1 = ( l + 1 + l ) > > 1 (l+1+l)>>1 (l+1+l)>>1 = l l l.
If you enter next l = m i d l=mid For the branch with l=mid, the feasible interval is not reduced, which will cause an endless loop.
If enter r = m i d − 1 r = mid-1 The branch of r=mid − 1 will cause l > r l>r l> R, end of cycle.
Therefore, the matching of the two forms is necessary
m
i
d
mid
The mid method is necessary and must be observed.

Note that we use in dichotomy
Shift right operation:
>
>
1
>>1
>>1, not integer division
/
2
/2
/2. The two are roughly the same, but there are slight differences.
| The right shift operation is rounded down, while the integer division is rounded to zero. When the binary value field contains negative numbers, the integer division cannot work normally. |
🌟 Dichotomy on real number field
The dichotomy in the real number field is relatively simple, and the required accuracy is determined e p s eps eps
with l + e p s < r l+eps<r L + EPS < R is the cycle condition, each time according to m i d mid Whether the judgment on mid is established or not, select r = m i d r=mid r=mid or l = m i d l=mid l=mid. Generally, it needs to be retained k k In case of k decimal places, take e p s = 1 0 − ( k + 2 ) eps = 10^{-(k+2)} eps=10−(k+2)
//If the title requires three decimal places
while(l + 1e-5 < r)
{
double mid = (l+r) / 2;//In the algorithm problem, it is recommended to use double, and float sometimes leads to slight deviation in the result due to accuracy problems
if(Judgment conditions) r = mid;
else l = mid;
}
Sometimes the accuracy is not easy to determine or express, so we can simply use the bisection method of fixed number of cycles, which is also a quite good strategy. The accuracy of the results obtained in this way is often better than the setting
e
p
s
eps
eps is higher.

for(int i = 0; i < 100;i++)
{
double mid = (l+r) /2;
if(Judgment conditions) r = mid;
else l = mid;
}
My friends should have a vague feeling now,
g
e
t
get
get the essence of dichotomy. Let's start to look at some exercises and really experience how to beat the dichotomy skill

💓 Strike while the iron is hot and start practicing
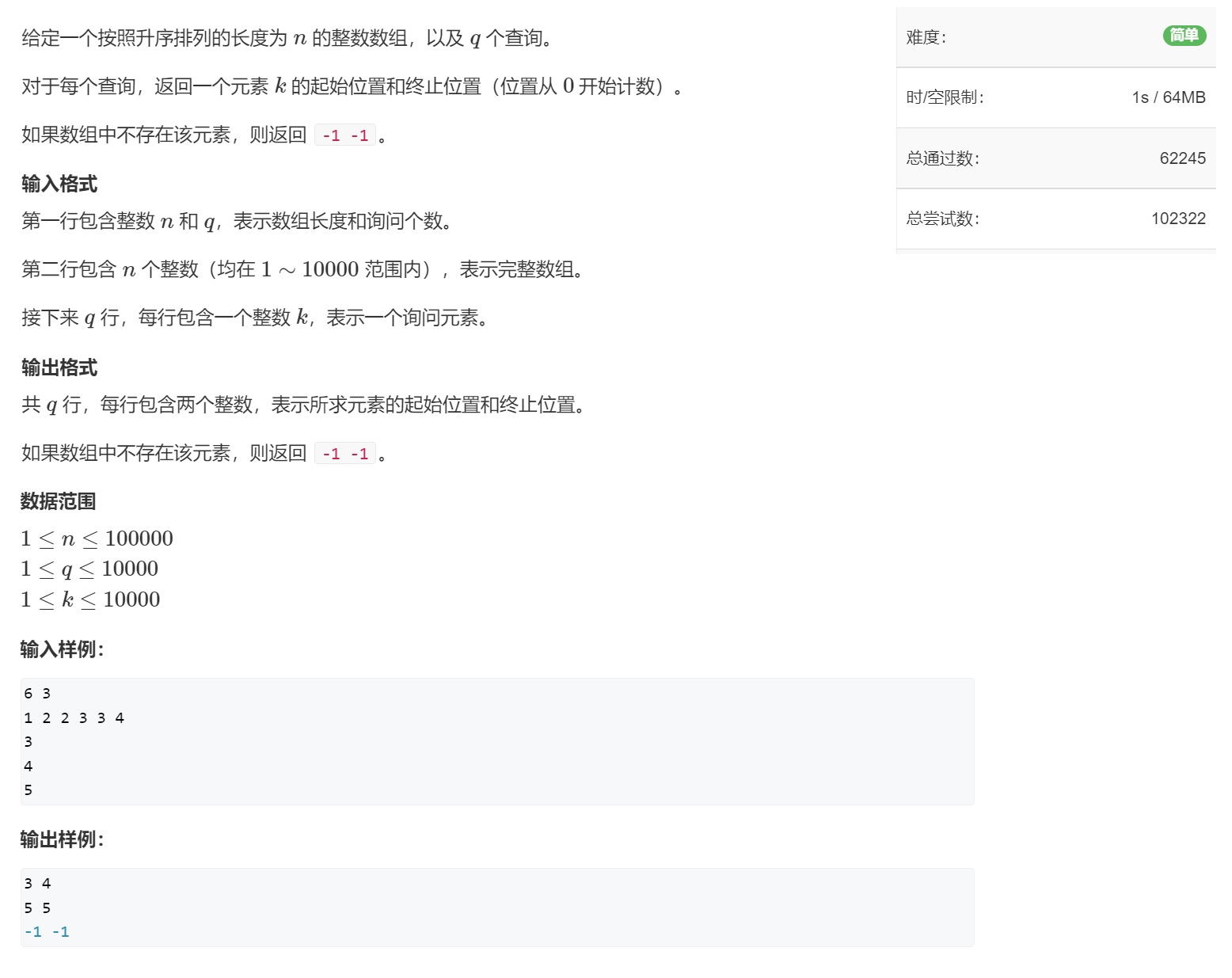
🌟 Example 1. Range of numbers
🌱 Title Description
🌴 shopping spree
| The title wants us to determine the starting position of the number we are looking for. To achieve this, we need to re understand the two situations of dichotomy. |

For case 1, in i f ( a [ m i d ] > = x ) if(a[mid] >= x) If (a [mid] > = x), then this lookup value x x x is to the left of the midpoint, which can be understood as determining the left boundary of the current interval
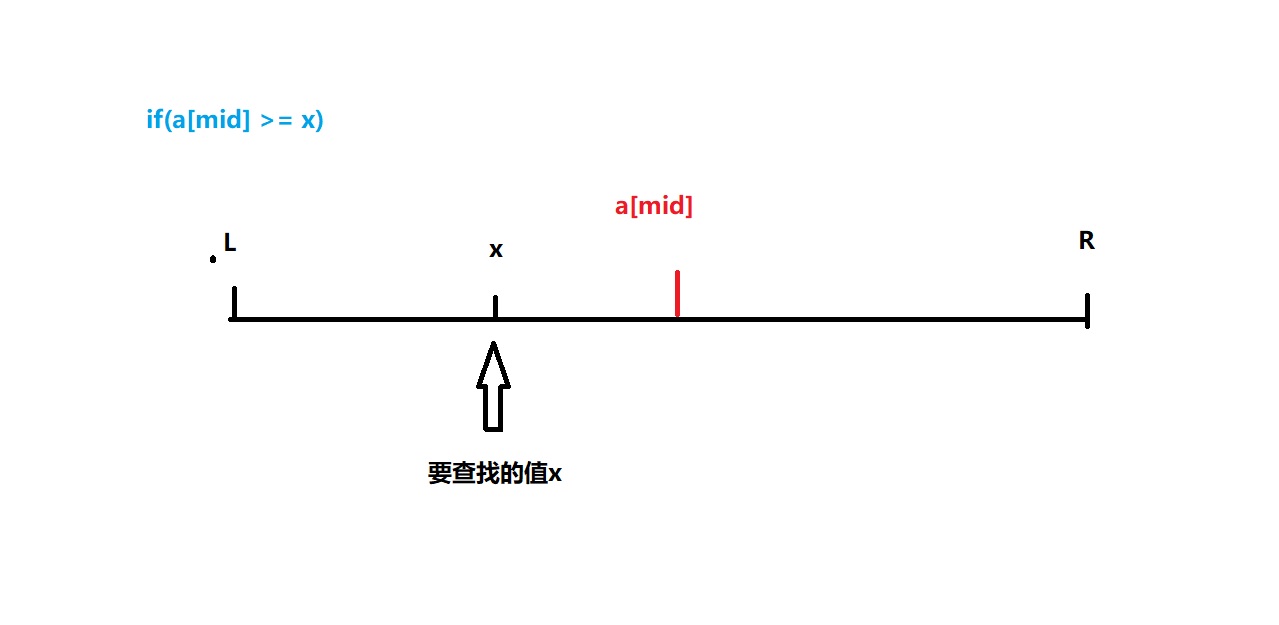
Similarly, with the same understanding of case 2, case 2 can be understood as determining the right boundary.
So it's easy to solve this problem. Just use the two cases in turn. Be careful not to reverse the order~
🌵 Reference code (C + + version)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010 ;
int q[N];
int n,m;
int main()
{
scanf("%d %d",&n,&m);
//Enter n pieces of information
for(int i= 0; i < n;i++) scanf("%d",&q[i]);
//m queries
for(int i = 0; i < m;i++)
{
int x;
scanf("%d",&x);
//Through drawing + theoretical analysis, in fact, I'm not angry
//Determine the left endpoint first
int l = 0, r = n-1;
while(l < r)
{
int mid = l + r >> 1;
//Compare this dichotomous mid with x
if(q[mid] >= x) r = mid;
else l = mid +1;
}
if(q[l] == x)
{
cout << l <<' ';
r = n-1;
//Determine right endpoint
while(l < r)
{
int mid = l+r+1 >> 1;//If we analyze it according to the previous understanding, we can directly write L + R > > 1 naked. Through the following code analysis, do you want to add 1
if(q[mid] <= x) l = mid;
else r = mid -1;
}
cout << r <<endl;
}else cout << "-1 -1" << endl;
}
return 0;
}
Kill the first monster ~, attack the next one

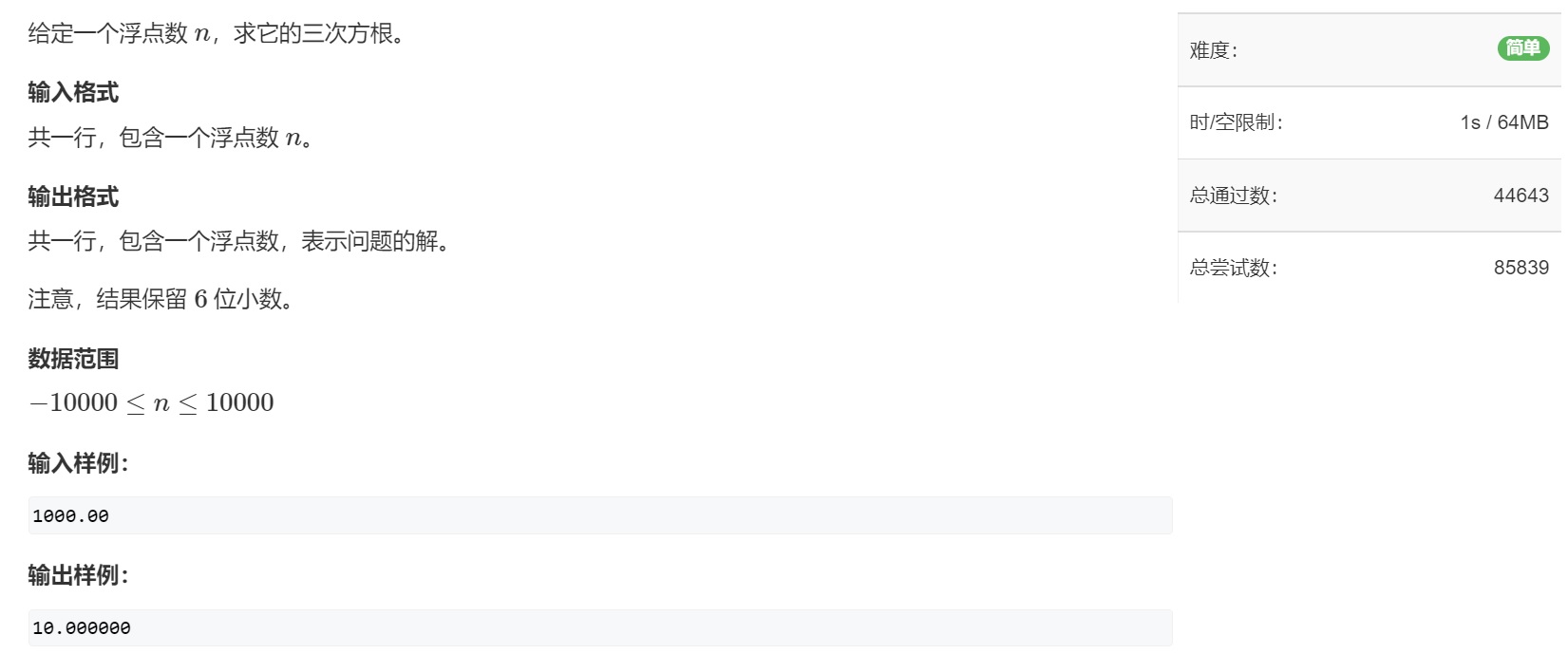
🌟 Example 2. The cubic root of a number
🌱 Title Description
🌴 shopping spree
What the topic gives us is a floating point number, that is, a binary belonging to the real number field. Then we only need to specify a judgment condition, and then continue to dichotomy to accuracy s p s sps Stop again to the extent of sps = 10-8.
Because let's find the cubic root of a number, then the judgment condition can be set as:
i
f
(
m
i
d
∗
m
i
d
∗
m
i
d
>
=
x
)
if(mid * mid * mid >= x)
if(mid∗mid∗mid>=x)
🌵 Reference code (C + + version)
#include <cstdio>
int main()
{
double x;
scanf("%lf",&x);
double l = -10000,r =10000;
while(r-l >= 1e-8)
{
double mid = (l+r) / 2;
if(mid*mid*mid >= x) r =mid;
else l = mid;
}
printf("%.6lf",l);
return 0;
}
Perfect solution

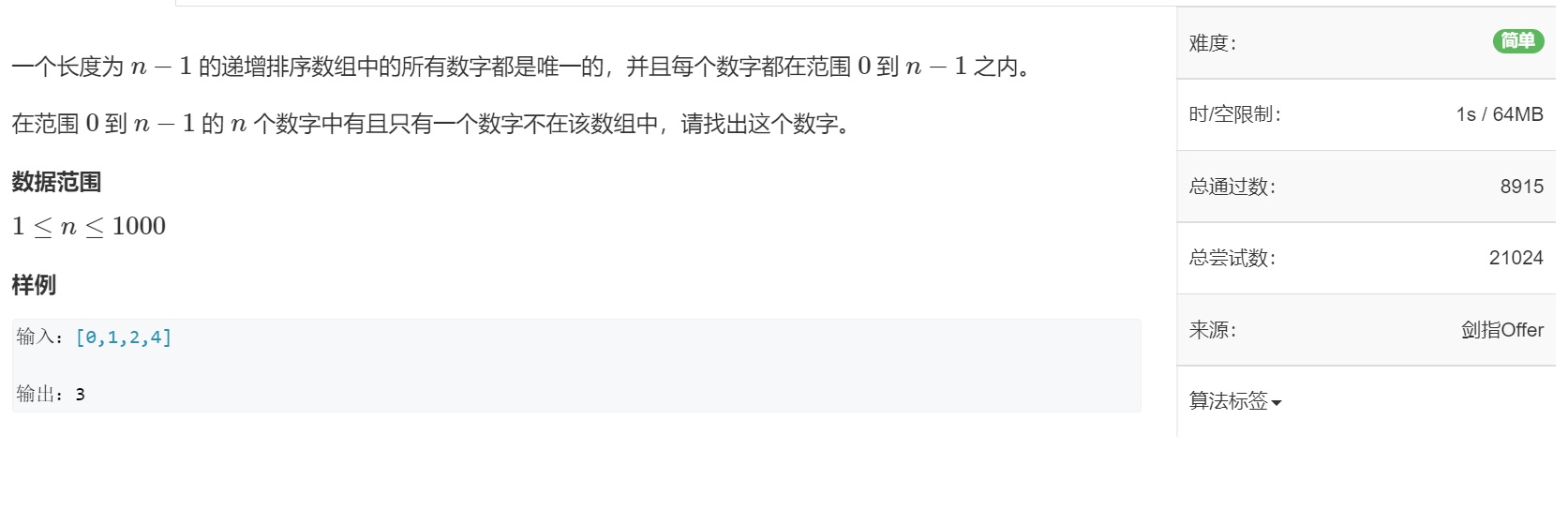
🌟 Example 3: missing numbers from 0 to n-1
🌱 Title Description
🌴 shopping spree
This topic is given an incremental array, assuming that the first missing number in the array is
x
x
x.
Then the actual situation of the subscript in the array and the number stored by the subscript is as follows:
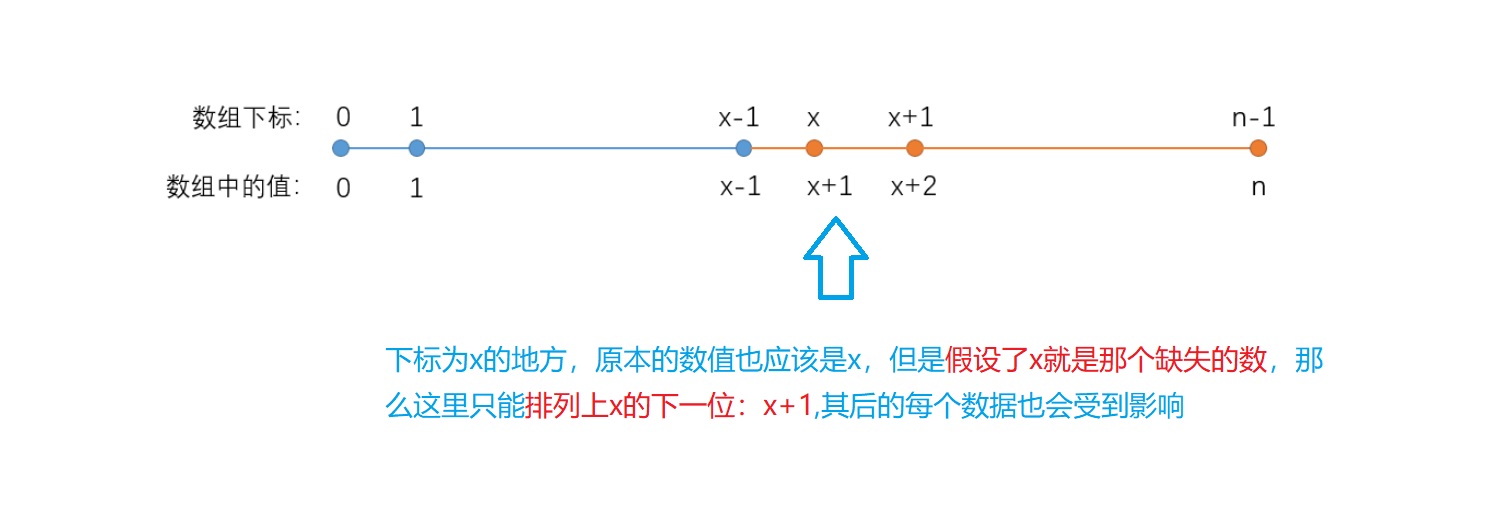
It can be observed that:
It can be seen that the blue part on the left of the array satisfies nums[i] == i;
The orange part on the right of the array does not satisfy nums[i] == i.
Therefore, we can take whether nums[i] == i as the dividing point to determine the dichotomy x x Judgment conditions of x

In addition, we should pay attention to the special case: when all numbers meet nums[i] == i, it means that what is missing is n n n
As for time complexity:
The binary iteration will only be executed
O
(
l
o
g
n
)
O(logn)
O(logn) times, then the time complexity
O
(
l
o
g
n
)
O(logn)
O(logn). In terms of time, there is no problem at all.
🌵 Reference code (C + + version)
class Solution {
public:
int getMissingNumber(vector<int>& nums) {
if(nums.empty()) return 0;
//Binary search
int l = 0 , r = nums.size()-1;
while(l < r)
{
int mid = (l+r) >> 1;
//If all the mid point values mid obtained from bisection are not equal to the corresponding data values, continue bisection search
if(nums[mid] != mid) r = mid;
else l = mid+1;
}
//Return results
if(nums[r] == r ) r++;
return r;
}
};
Happy Ac

🌟 Example 4. Number finding of test question algorithm training 2
🌱 Title Description
🌴 shopping spree
After reading the question, we can understand that this question is to let us find the position of a number:
If this number is found in a string of data, the output position (note that the position starts from 1); If this number is not found, determine where the input data should be inserted.
For the requirements found, dichotomy can be used to complete them efficiently.
Use case 1 and case 2 are OK. Pay attention to the boundary.
| For determining the insertion position, my idea is to enumerate directly one by one and compare the number with the smallest difference from the input data. When it is found, the number with the smallest difference and the difference greater than zero is the appropriate position. |

Combined with the examples, implement what I just said. I only listen to the very empty description. I don't like the very empty things myself.
sample input 10 23 34 56 78 99 123 143 155 167 178 128 sample output 7
For example, in this example, the difference between input data 128 and 123 is 5, which is a positive integer with the smallest difference. The position of 123 is 6, and the next one behind it is 7.
🌵 Reference code (C + + version)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1010;
int q[N];
int n,mid;
int main()
{
int x;
int ans = 0x3f3f3f3f;
int pos = 0;
scanf("%d",&n);
//Input data
for(int i =0; i < n;i++) scanf("%d",&q[i]);
scanf("%d",&x);
//Start dichotomy
int l = 0, r = n-1;
while(l < r)
{
mid = (l + r) >> 1;
if(x <= q[mid]) r = mid;
else l = mid +1;
}
//Two points, output position
if(x == q[l]) printf("%d",l+1);
else //If you don't get the number you want to find, insert it
{
for(int i = 0; i < n;i++)
{
//A small optimization is also a case of processing larger data than the last one
if(x > q[n-1])
{
pos = n;
break;
}else
if(ans > 0 && x- q[i] < ans)
{
ans = x-q[i];
pos = i;//Record location
}
}
//output location
printf("%d",pos+1);
}
return 0;
}
From the above small examples, we should gradually realize that dichotomy occupies a place in the search field. Because its time complexity is O ( l o g n ) O(logn) O(logn).
For example, the telephone line from Shanghai to Hangzhou is broken, with 300000 electric poles. If you enumerate them one by one, it is 300000 times.
If you use dichotomy to find it, it only takes about 20 times. The efficiency is considerable.

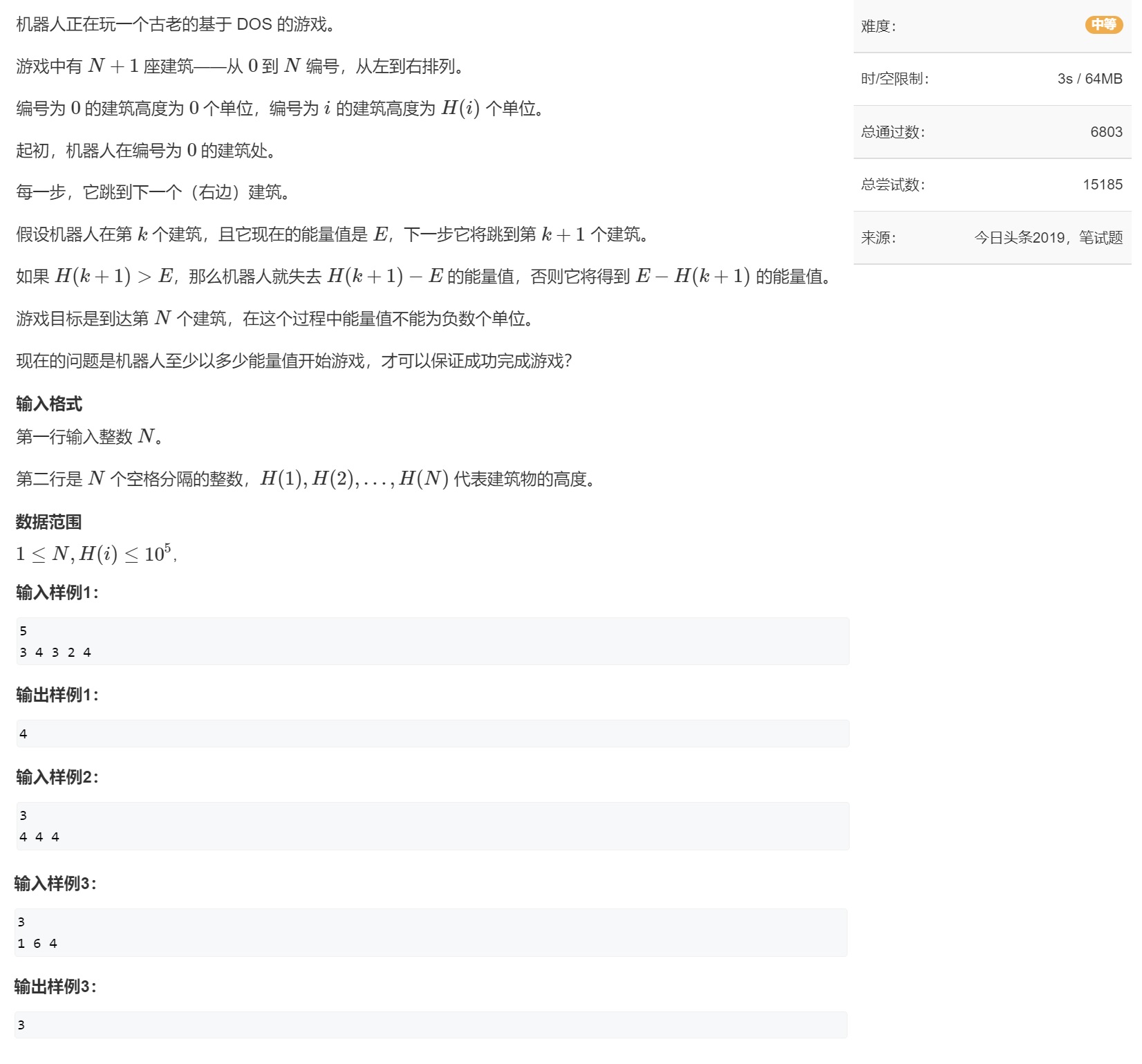
🌟 Example 5. Today's headlines 2019 robot jumping problem
🌱 Title Description
🌴 shopping spree
1, Ranging algorithm from data
The data range of the topic is 1 to 100000, according to my The breath of water One type recursion The forms listed in can be divided into two parts. Compared with other algorithms, binary implementation is relatively easier. Let's solve it according to the idea of binary.

The question in the output format indicates that the integer should be output, so this question belongs to integer dichotomy

2, Topic analysis
The energy consumption of robot in the title can be roughly understood as:
Jumping up can consume energy, so you need to subtract; As for the energy that can be obtained by jumping down, you need to add.
So,
If
H
(
k
+
1
)
>
E
H(k+1) > E
H (K + 1) > e, then:
E
=
E
−
(
H
(
k
+
1
)
−
E
)
E = E-(H(k+1)-E)
E=E−(H(k+1)−E) =
2
∗
E
−
H
(
k
+
1
)
2*E-H(k+1)
2∗E−H(k+1)
If
H
(
k
+
1
)
<
E
H(k+1) < E
H (K + 1) < e, then:
E
=
E
+
E
−
H
(
k
+
1
)
E = E+E-H(k+1)
E=E+E−H(k+1) =
2
∗
E
−
H
(
k
+
1
)
2*E-H(k+1)
2∗E−H(k+1)
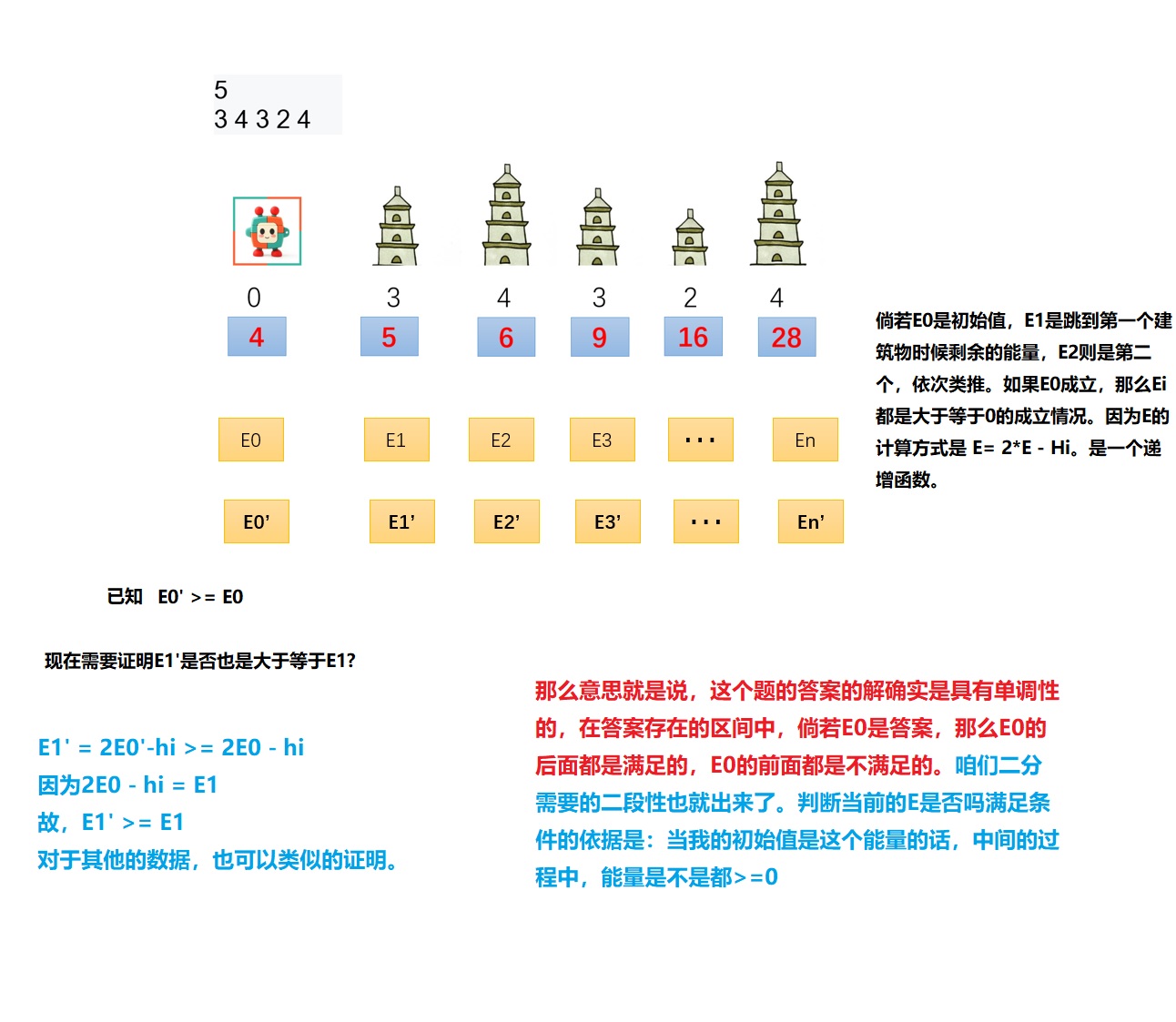
Through the analysis of the energy change in the topic, it is concluded that the calculation method of energy change is the same whether jumping to a higher building or to a lower tower.
Let's use this formula to simulate the example of the problem.
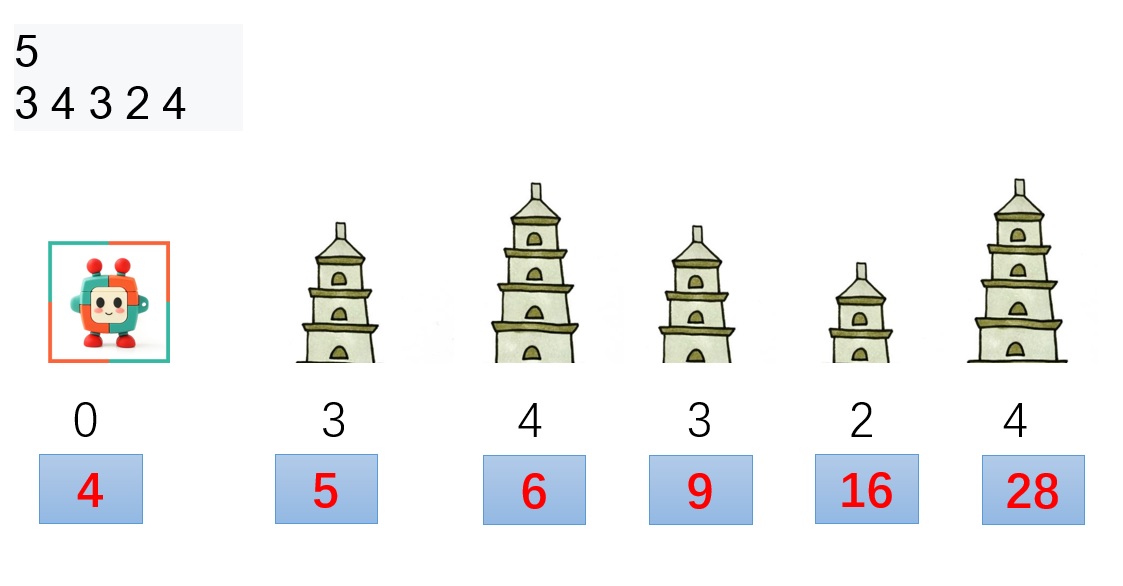
It can be seen that the energy specified in the title in the whole link will not be negative, so the initial energy can be 4.
If the initial energy is 3, then the energy will be negative
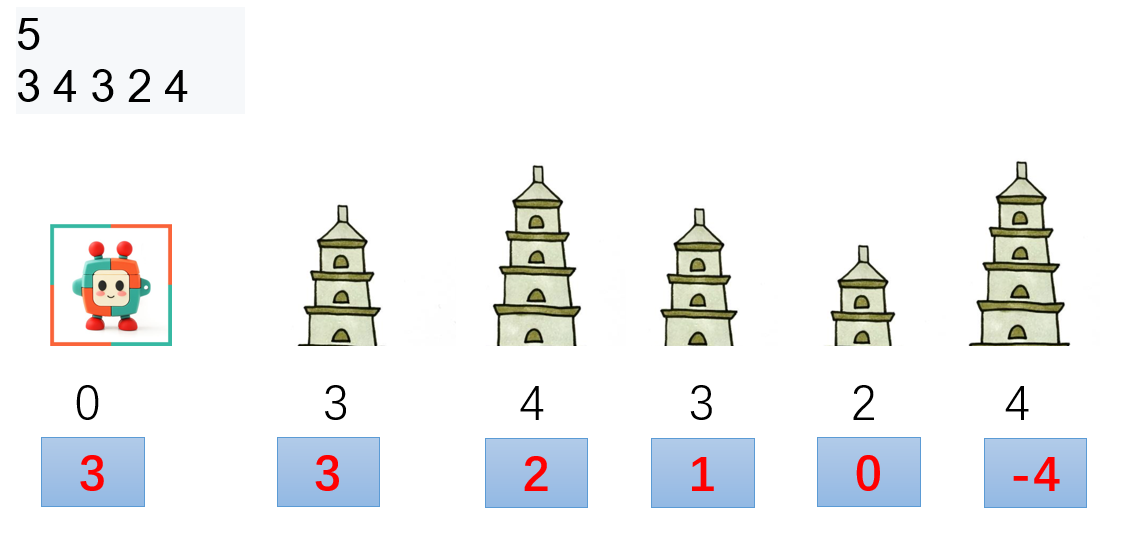
3, Determine the nature
nature. Find monotonicity. If there is monotonicity, you can use dichotomy. The nature of the data segment can be found, or it does not satisfy the nature of the data segment.
If initial value
E
0
E_0
E0 # meets the requirements and now exists
E
0
′
E'_0
E0′ >=
E
0
E_0
E0, if
E
0
′
E'_0
E0 'can also meet the requirements, so it is monotonic. therefore
E
0
E_0
E0 , should be the minimum value, so we can divide it in two.
Extension: proof of monotonicity of this question (interested partners can)
4, Determine the form of dichotomy
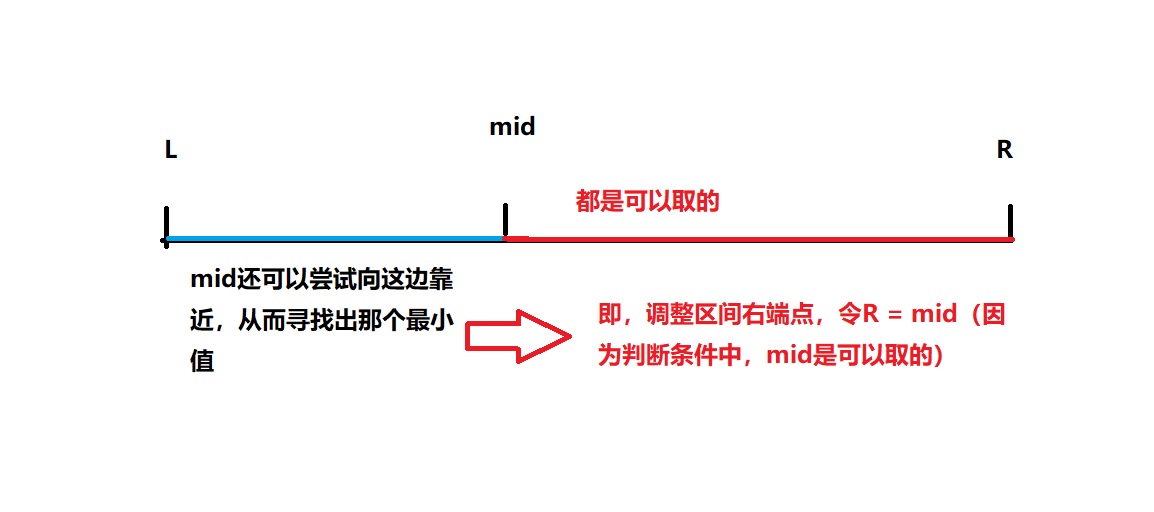
Is it case one or case two? That is, what is it r = m i d r = mid r=mid or l = m i d l = mid l=mid

If the function used for judgment is called
c
h
e
c
k
(
)
check()
check().
If
c
h
e
c
k
(
m
i
d
)
check(mid)
check(mid) holds, meaning
m
i
d
mid
mid is available. that
m
i
d
mid
The right side of mid can be accessed. In order to more accurately determine the data to be searched, the right section should be adjusted, i.e
r
=
m
i
d
r=mid
r=mid.
V
c
h
e
c
k
check
Implementation of check function
Pass on the incoming data to judge whether there is 0 during the period. If 0 appears, the current scheme is inappropriate.
🌵 Reference code (C + + version)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int h[N];
bool check(int e)
{
//Recursive enumeration
for(int i = 1; i <= n;i++)
{
e = e*2 -h[i];
//(E > = 1E5) the response is that when the calculated e at a certain time is greater than the maximum height maxh, the data behind this E
//It must also meet the requirements. You can directly return true; So as to realize optimization and prevent int ermediate process explosion
if(e >= 1e5) return true;
if(e < 0) return false;//0 appears and false is returned
}
return true;
}
int main()
{
scanf("%d",&n);
for(int i = 1;i <= n;i++) scanf("%d",&h[i]);
//Determine boundary
int l = 0, r = 1e5;
while(l <r)
{
int mid = l+r >>1;
if(check(mid)) r = mid;
else l = mid+1;
}
//Output answer
printf("%d",l);
return 0;
}
🌟 Example 6. Sum of squares of group C++A/B in the 7th Lanqiao cup provincial competition
🌱 Title Description
🌴 Problem solving report (two tips)
1, The number of enumerations depends on the data range
The title says: every positive integer can be expressed as at most
4
4
Sum of squares of four positive integers.
The data range given to us is 0<
N
N
N <
5
∗
1
0
6
5∗10^6
5∗106.
So for each number
a
,
b
,
c
,
d
a,b,c,d
a. For b, c and d, the range that can be taken should all be 0~
N
\sqrt N
N
, it's between 2000 and 3000. Take out a calculator that can calculate about 2236 more specifically.

Here you can use a technique to determine the maximum number of enumerable numbers through the data range.
If you want to enumerate directly, you should enumerate three numbers: a , b , c a,b,c a,b,c
So the time complexity is
233
6
3
2336^3
23363, even if you take a change, it's OK
200
0
3
2000^3
20003, will also be carried out
8
∗
1
0
9
8*10^9
8 * 109 operations, directly exceeding the 100 million operations that C + + can perform in one second. So we can only enumerate two numbers at most.

2, Space for time
Space for time is an idea often used in algorithm problems. It is recommended to take it. Time is more important in algorithm problems.
The specific method is to enumerate two numbers first, such as enumeration
c
and
d
c and d
c and d. Their calculation results
c
2
+
d
2
c^2+d^2
c2+d2 stored. Then enumerate
a
and
b
a and b
a and b, at this time, only use the stored data to find the appropriate data.

3, Search method
| When it comes to search methods, the easiest to think of should be hash and bisection. I'll focus on implementing the binary code here. I put the hash code in gitee, and friends can pick it by themselves. |
4, Overload less than symbol
Because save
c
2
+
d
2
c^2+d^2
After the sum of c2+d2, it will be used to find
a
2
+
b
2
a^2+b^2
a2+b2 link from small to large. Therefore, to sort the stored data, it is necessary to re specify the comparison method of less than symbol.

🌵 Reference code (C + + version)
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5e6+10;
//Open a structure to store the information of c^2+d^2
struct Sum{
int s,c,d;
//Because it is necessary to sort the information of c^2+d^2 later, the less than symbol needs to be redefined
bool operator <(const Sum &tmp) const
{
if(s != tmp.s) return s < tmp.s;//Sort the sum from small to large first
if(c != tmp.c) return c < tmp.c;//If the sum is the same, it is sorted according to c from small to large
return d < tmp.d;//If the sum c is the same, it is sorted from small to large according to d
}
}s[N];
int n,cnt;
int main()
{
cin >> n;
//Start enumerating and storing information about c and d
for(int c = 0; c * c<= n;c++)
for(int d = c; c*c + d*d <= n;d++)
{
s[cnt++] = {c*c+d*d,c,d};
}
sort(s,s+cnt);
//Enumerate a and b and use binary lookup in them
for(int a = 0; a * a <= n;a++)
for(int b = a; a*a + b*b <= n;b++)
{
//Calculate the travel value, and then find it in the s array
int t = n-a*a-b*b;
int l = 0,r = cnt -1;
while(l <r)
{
int mid = (l+r) >>1;
//Similar to the above examples, the value t to be found is to the left of the midpoint mid, so adjust the right endpoint.
if(s[mid].s >= t) r = mid;
else l = mid+1;
}
//If you find a set of solutions, you can output the results, because you need the one with the smallest dictionary order
if(s[l].s == t)
{
printf("%d %d %d %d\n",a,b,s[l].c,s[l].d);
return 0;
}
}
}
Here is the code for searching by hash:
Hash solution of array simulation

I've brushed so many strange things in a row. I'll blow up after a rest~
🌟 Example 7. The eighth Blue Bridge Cup provincial competition C++A/B component chocolate
🌱 Title Description
🌴 shopping spree
This problem, also let us find a suitable side length for chocolate. The data range is 100000. It is easy to find the appropriate data with two points.

Details needing attention:
When screening the appropriate side length of chocolate, it is necessary to
H
[
i
]
H[i]
H[i] and
W
[
i
]
W[i]
W[i] statistics,
Namely
(
H
[
i
]
/
pass
enter
of
edge
long
)
∗
(H[i] / incoming side length)*
(H[i] / incoming side length) *
(
W
[
i
]
/
pass
enter
of
edge
long
)
(W[i] / incoming side length)
(W[i] / incoming side length)
Cannot be written as:
(
H
[
i
]
∗
W
[
i
]
)
/
(H[i] * W[i])/
(H[i]∗W[i])/
(
pass
enter
of
edge
long
∗
pass
enter
of
edge
long
)
(incoming side length * incoming side length)
(incoming side length * incoming side length). This is because the precision of integer division is inaccurate due to rounding down.
🌵 Reference code (C + + version)
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100010;
int h[N],w[N];
int n,k;
bool check(int a)
{
//According to the statistics of the current side length a, can you distinguish k pieces of chocolate greater than or equal to the requirements of the topic
int sum = 0;
//Enumerate the information of n chocolates
for(int i = 0;i < n;i++)
{
//Count how many a can be carried in h and w respectively
sum += (h[i]/a)*(w[i]/a);
if(sum >= k) return true;
}
return false;
}
int main()
{
cin >> n >>k;
//Enter information for n chocolates
for(int i = 0; i < n;i++) cin >> h[i] >> w[i];
//Enter the two-part link and find out the appropriate size
//Input to ensure that each child can get at least one dollar × 1 chocolate. All left endpoints have a minimum of 1
int l = 1, r = 100000;
while(l < r)
{
int mid = (l+r+1) >> 1;
//If this check function holds, it is proved that the current midpoint mid should be to the left of the maximum side length x to be searched,
//To determine x further, you should adjust the left boundary. So when you take mid from the top, you need to add 1
if(check(mid)) l= mid;
else r = mid -1;
}
cout << l <<endl;
}
In the twinkling of an eye, it has reached the eighth level. It's so fast

🌟 Example 8. Remove the important stones in the algorithm training of test questions
🌱 Title Description
🌴 shopping spree
The topic asks us to find the most labor-saving solution to help this rather lazy fairy throw stones into the world

| Let's find the most labor-saving scheme, which means taking this scheme as the dividing line, the front part of it does not meet the requirements, and the back part of it meets the requirements, but it may not be cost-effective. |
Then, at this time, the problem has two paragraphs, and we can hold our breath and play our two-point skill to find out the most labor-saving scheme with two points.

Now the only thing to solve is right i f if Judgment function in if c h e c k check check implementation.
c h e c k check The core of the operation of the check function is to judge the current binary m i d mid Can the mid value help the lazy fairy in the specified k k Remove all stones in k times.
🌵 Reference code (C + + version)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N=1022;
int n,m;
int a[N];
bool check(int d)
{
int sum = 0,cnt =0,i =1;
//This check function checks whether each time you move a stone with the power of d, you can move all the stones in m
while(a[i])//Continue when there are stones
{
if(sum+a[i] <= d) //It means to judge how many pieces can be moved in succession
{
sum += a[i];
i++;
}
//When you can't move it continuously, check whether the stone is directly greater than the spiritual power
else if(a[i] > d) return false;//If it is directly greater than the spiritual power, then this scheme can't work. It directly returns false
else//Otherwise, proceed to the next round
{
cnt ++; //The counter is used to judge whether the task is completed in the specified k times
sum = 0;//Reset sum
}
}
return cnt < m;//Judge whether the maximum m times of spiritual power is met
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
int l=0,r=1000000;
while(l<r){
int mid= (l+r)/2;
if(check(mid))r=mid;
else l = mid + 1;
}
cout<<l;
return 0;
}
💓 summary
Well, so far, the practice of the second form of insect breathing in the middle of the butterfly has come to an end. Do you all live up to your beautiful sister

Here's a summary:
| 1. For dichotomy, whether dichotomy can be used can be seen from the data range, or you can know the answer after reading the question, or if the scheme is segmented and monotonous, dichotomy can also be used. |
| 2. The most widely used field of dichotomy should be search. Therefore, when we see the problem and want us to find a maximum and minimum number, we can make a small abacus of dichotomy. But it doesn't have to be limited to two points. Hash also dominates the world in search. It would be better if the violence enumeration could be solved |

3. Remember the two situations of dichotomy
Combining the two situations of graph memory dichotomy;
Combining the two situations of graph memory dichotomy; Combined with the two cases of graph memory dichotomy. Say something important three times.The picture of situation 1 is like this:
The diagram of case 2 is like this:
If we deal with the boundary problem of these two cases, we can handle the dichotomy well.

It's time to say goodbye to sister Ren, get out of the butterfly house and prepare for the infinite train where Mr. purgatory is~