preface
If you think the article is helpful, please leave some praise and collection. Pay attention to xiaoleng and read more dry goods learning articles
★ this is Xiao Leng's blog ‡ see the column for good articles on high-quality technology The official account of the individual, sharing some technical articles, and the pit encountered. Current series: data structure series Source code git warehouse Data structure code address Code Git warehouse address
catalogue
Introduction to binary tree
Why do you need a tree data structure?
Concept of binary tree
- There are many kinds of trees, and each node can only have two child nodes at most. One form is called binary tree.
- The child nodes of binary tree are divided into left node and right node
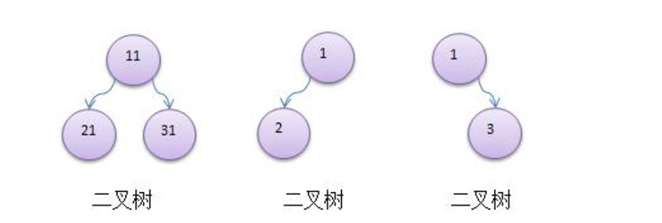
3. If all leaf nodes of the binary tree are in the last layer, and the total number of nodes = 2 ^ n - 1, n is the number of layers, then we call it a full binary tree.
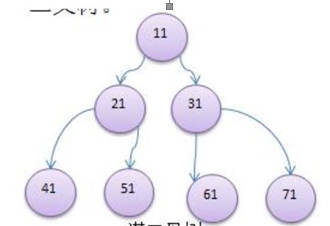
4. If all leaf nodes of the binary tree are in the last layer or the penultimate layer, and the leaf nodes of the last layer are continuous on the left, it is penultimate The leaf nodes of the layer are continuous on the right, which is called complete binary tree
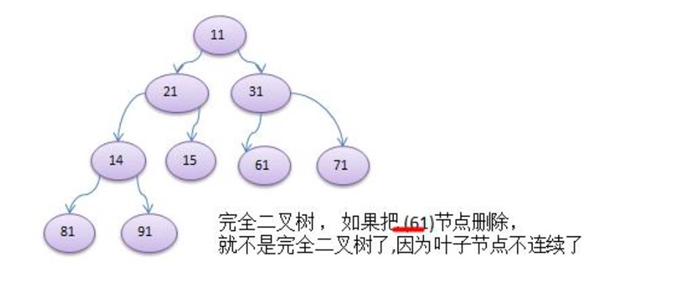
array
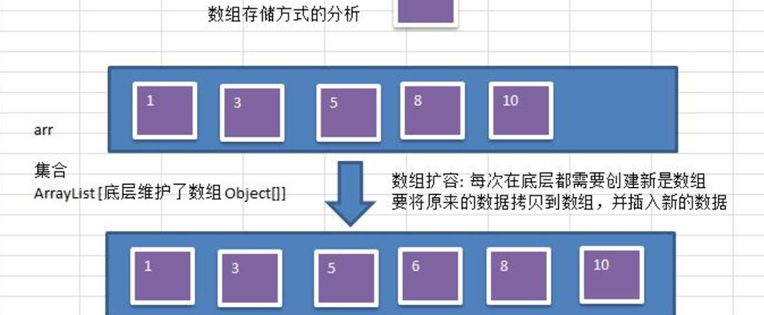
Analysis of array storage mode
Advantages: it is fast to access elements by subscript. For ordered arrays, binary search can also be used to improve the retrieval speed. Disadvantages: if a specific value is to be retrieved, or the inserted value (in a certain order) will move as a whole, which is inefficient
Draw the operation diagram:
Linked list
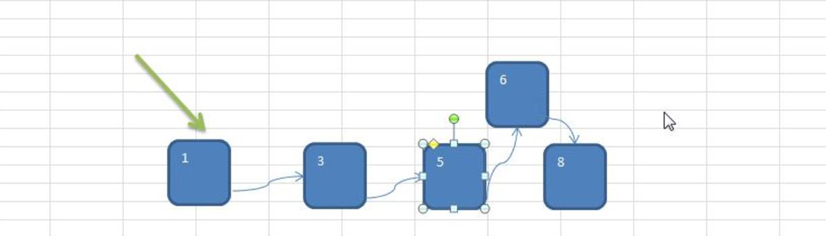
Analysis of chain storage mode
Advantages: to a certain extent, the storage mode of the array is optimized (for example, if you insert a numeric node, you only need to link the inserted node to the linked list,
Deletion efficiency is also very good).
Disadvantages: when searching, the efficiency is still low, for example (to retrieve a value, you need to traverse from the beginning of the node)
Operation diagram:
Binary tree
Analysis of tree storage mode
It can improve the efficiency of data storage and reading. For example, using binary sort tree can not only ensure the retrieval speed of data, but also
It can ensure the speed of data insertion, deletion and modification
Case: [7, 3, 10, 1, 5, 9, 12]
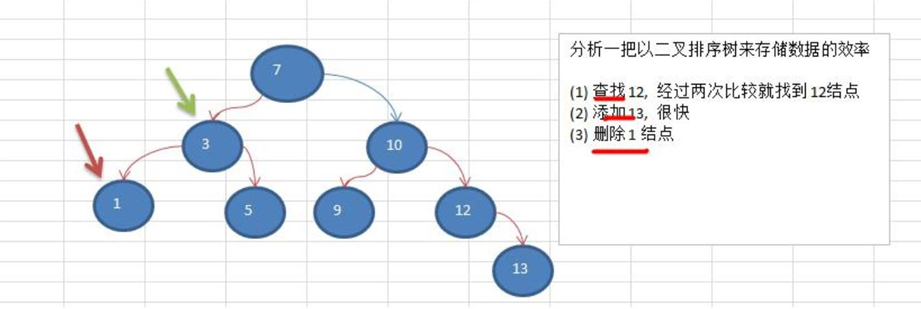
Cognitive tree structure
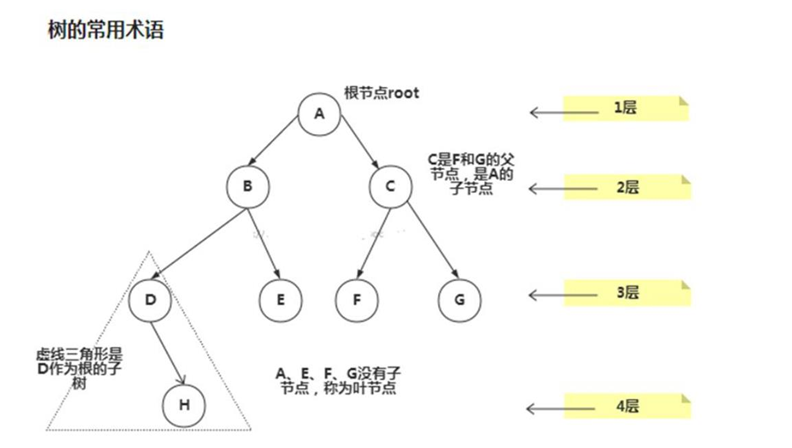
Common terms of tree (understood in combination with schematic diagram):
1) node 2) Root node 3) Parent node 4) Child node 5) Leaf node (Nodes without child nodes) 6) Weight of node(Node value) 7) route(from root Node finds the route of the node) 8) layer 6) subtree 7) Height of tree(Max layers )
- Forest: a forest composed of several sub trees
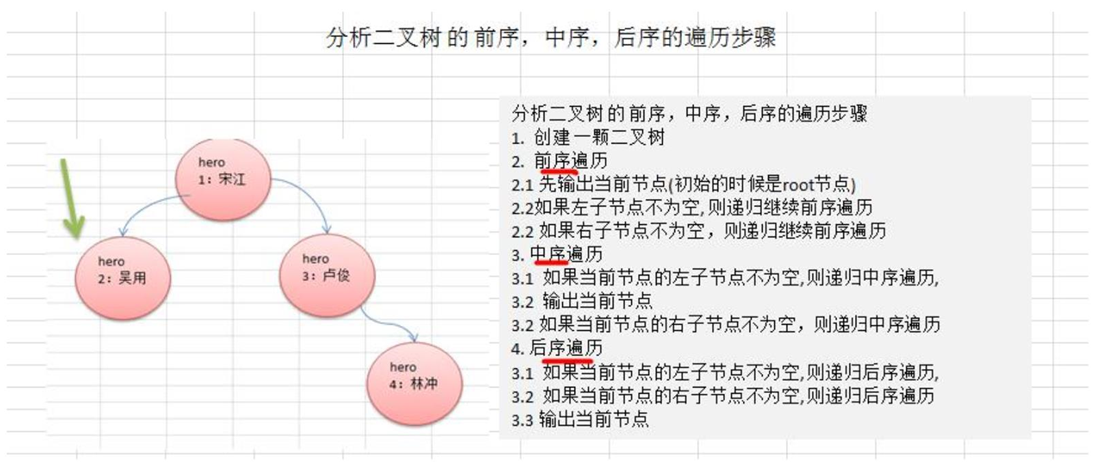
Description of binary tree traversal
- Preorder traversal: first output the parent node, and then traverse the left and right subtrees
- Middle order traversal: first traverse the left subtree, then output the parent node, and then traverse the right subtree
- Post order traversal: first traverse the left subtree, then traverse the right subtree, and finally output the parent node
- Summary: see the order of output parent nodes to determine whether it is pre order, middle order or post order
Binary tree traversal application examples (pre order, middle order, post order)
Binary tree traversal code example
public static void main(String[] args){
// Test, first create a binary tree
BinaryTree binaryTree = new BinaryTree();
heroNode root = new heroNode(1, "Song Jiang");
heroNode node1 = new heroNode(2, "Wu Yong");
heroNode node2 = new heroNode(3, "Lu Junyi");
heroNode node3 = new heroNode(4, "Lin Chong");
heroNode node4 = new heroNode(5, "Guan Sheng");
//Set header node
binaryTree.setHead(root);
// Here we fill the binary tree manually, and then we will fill the binary tree recursively
root.setLeftNode(node1);
root.setRightNode(node2);
node2.setRightNode(node3);
node2.setLeftNode(node4);
//test
Preorder traversal
//binaryTree.PreOrder();
Middle order traversal
//System.out.println();
//binaryTree.InfixOrder();
Postorder traversal
//System.out.println();
//binaryTree.PostOrder();
}
class BinaryTree {
//Determine root node
private heroNode head;
public void setHead(heroNode head) {
this.head = head;
}
// Preorder traversal
public void PreOrder() {
if (this.head != null) {
this.head.PreOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Middle order traversal
public void InfixOrder() {
if (this.head != null) {
this.head.infixOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Subsequent traversal
public void PostOrder() {
if (this.head != null) {
this.head.postOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
}
class heroNode {
private int id;
private String name;
private heroNode leftNode;
private heroNode rightNode;
public heroNode getLeftNode() {
return leftNode;
}
public void setLeftNode(heroNode leftNode) {
this.leftNode = leftNode;
}
public heroNode getRightNode() {
return rightNode;
}
public void setRightNode(heroNode rightNode) {
this.rightNode = rightNode;
}
public heroNode(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
@Override
public String toString() {
return "heroNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
public void setName(String name) {
this.name = name;
}
// Preorder traversal
public void PreOrder() {
System.out.println(this);
if (this.getLeftNode() != null) {
this.leftNode.PreOrder();
}
if (this.getRightNode() != null) {
this.rightNode.PreOrder();
}
}
// Middle order traversal
public void infixOrder() {
if (this.leftNode != null) {
this.leftNode.infixOrder();
}
System.out.println(this);
if (this.rightNode != null) {
this.rightNode.infixOrder();
}
}
// Postorder traversal
public void postOrder() {
if (this.leftNode != null) {
this.leftNode.postOrder();
}
if (this.rightNode != null) {
this.rightNode.postOrder();
}
System.out.println(this);
}
}Binary tree search idea
- Please write the methods of pre order search, middle order search and post order search.
- Three search methods are used to find the node with heroNO = 5
- And analyze various search methods, and compare how many times
Train of thought diagram
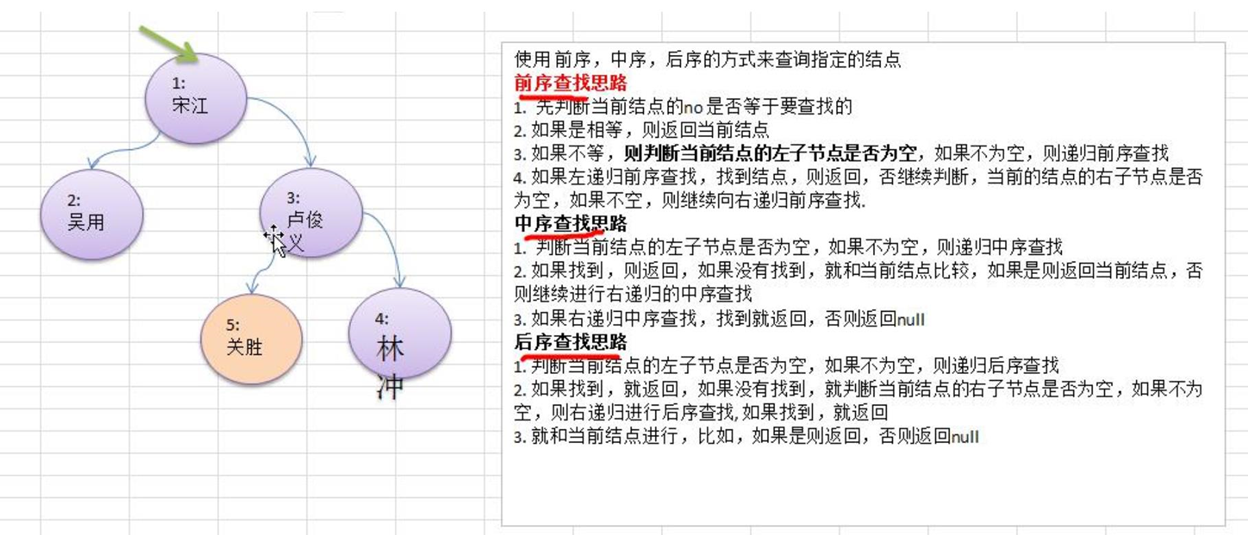
Binary tree lookup code example
In order to facilitate better reading the code, the search code of nodes and tree classes will be specially written, followed by the whole code
class BinatyTree{
//Preorder search
public heroNode preOrderSearch(int no) {
if (this.head != null) {
return this.head.PreOrderSearch(no);
} else {
return null;
}
}
//Medium order search
public heroNode infixOrderSearch(int no) {
if (this.head != null) {
return this.head.infixOrderSearch(no);
} else {
return null;
}
}
//Sequential search
public heroNode postOrderSearch(int no) {
if (this.head != null) {
return this.head.postOrderSearch(no);
} else {
return null;
}
}
}
class heroNode{
//Preorder search
public heroNode preOrderSearch(int no) {
if (this.head != null) {
return this.head.PreOrderSearch(no);
} else {
return null;
}
}
//Medium order search
public heroNode infixOrderSearch(int no) {
if (this.head != null) {
return this.head.infixOrderSearch(no);
} else {
return null;
}
}
//Sequential search
public heroNode postOrderSearch(int no) {
if (this.head != null) {
return this.head.postOrderSearch(no);
} else {
return null;
}
}
}Binary tree - delete node
- If the deleted node is a leaf node, delete the node
- If the deleted node is a non leaf node, the subtree is deleted
- Test, delete No. 5 leaf node and No. 3 subtree
Train of thought analysis
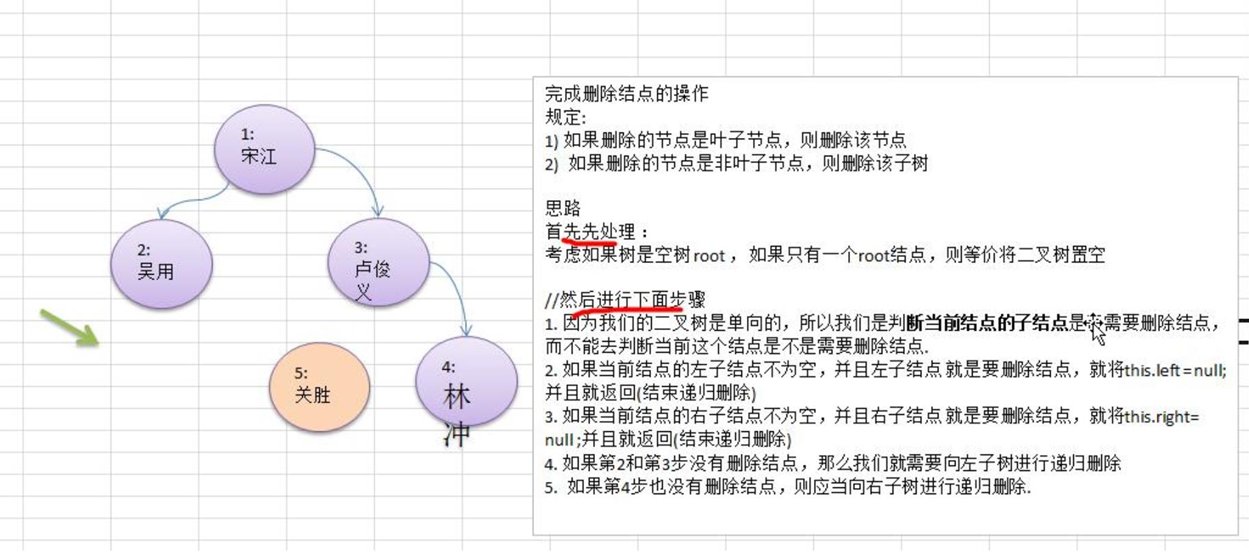
Binary tree, traversal, search, delete the whole code
package com.hyc.DataStructure.tree;
/**
* @projectName: DataStructure
* @package: com.hyc.DataStructure.tree
* @className: BinaryTreeDemo
* @author: Cold Huanyuan doorwatcher
* @description: TODO
* @date: 2022/2/3 16:47
* @version: 1.0
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
// Test, first create a binary tree
BinaryTree binaryTree = new BinaryTree();
heroNode root = new heroNode(1, "Song Jiang");
heroNode node1 = new heroNode(2, "Wu Yong");
heroNode node2 = new heroNode(3, "Lu Junyi");
heroNode node3 = new heroNode(4, "Lin Chong");
heroNode node4 = new heroNode(5, "Guan Sheng");
//Set header node
binaryTree.setHead(root);
// Here we fill the binary tree manually, and then we will fill the binary tree recursively
root.setLeftNode(node1);
root.setRightNode(node2);
node2.setRightNode(node3);
node2.setLeftNode(node4);
//test
Preorder traversal
//binaryTree.PreOrder();
Middle order traversal
//System.out.println();
//binaryTree.InfixOrder();
Postorder traversal
//System.out.println();
//binaryTree.PostOrder();
//System.out.println("front, middle and back search");
//System.out.println("start pre order search");
//heroNode resNode = binaryTree.preOrderSearch(5);
//if (resNode != null) {
// System.out.printf("found node is no = >% D, name = >% s", resnode. Getid(), resnode getName());
//} else {
// System.out.println("search failed");
//}
//System.out.println("start middle order search");
//heroNode resNode = binaryTree.infixOrderSearch(5);
//if (resNode != null) {
// System.out.printf("found node is no = >% D, name = >% s", resnode. Getid(), resnode getName());
//} else {
// System.out.println("search failed");
//}
//System.out.println("start post order search");
//heroNode resNode = binaryTree.postOrderSearch(5);
//if (resNode != null) {
// System.out.printf("found node is no = >% D, name = >% s", resnode. Getid(), resnode getName());
//} else {
// System.out.println("search failed");
//}
// Delete test
System.out.println("Before deletion");
binaryTree.PreOrder();
System.out.println("After deletion");
binaryTree.deleteNode(5);
binaryTree.PreOrder();
}
}
class BinaryTree {
//Determine root node
private heroNode head;
public void setHead(heroNode head) {
this.head = head;
}
// Preorder traversal
public void PreOrder() {
if (this.head != null) {
this.head.PreOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Middle order traversal
public void InfixOrder() {
if (this.head != null) {
this.head.infixOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Subsequent traversal
public void PostOrder() {
if (this.head != null) {
this.head.postOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Preorder search
public heroNode preOrderSearch(int no) {
if (this.head != null) {
return this.head.PreOrderSearch(no);
} else {
return null;
}
}
//Medium order search
public heroNode infixOrderSearch(int no) {
if (this.head != null) {
return this.head.infixOrderSearch(no);
} else {
return null;
}
}
//Sequential search
public heroNode postOrderSearch(int no) {
if (this.head != null) {
return this.head.postOrderSearch(no);
} else {
return null;
}
}
// Delete node
public void deleteNode(int no) {
if (head != null) {
if (head.getId() == no) {
head = null;
return;
} else {
head.deleteNode(no);
}
} else {
System.out.println("Empty tree,Cannot delete");
}
}
}
class heroNode {
private int id;
private String name;
private heroNode leftNode;
private heroNode rightNode;
public heroNode getLeftNode() {
return leftNode;
}
public void setLeftNode(heroNode leftNode) {
this.leftNode = leftNode;
}
public heroNode getRightNode() {
return rightNode;
}
public void setRightNode(heroNode rightNode) {
this.rightNode = rightNode;
}
public heroNode(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
@Override
public String toString() {
return "heroNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
public void setName(String name) {
this.name = name;
}
// Preorder traversal
public void PreOrder() {
System.out.println(this);
if (this.getLeftNode() != null) {
this.leftNode.PreOrder();
}
if (this.getRightNode() != null) {
this.rightNode.PreOrder();
}
}
// Middle order traversal
public void infixOrder() {
if (this.leftNode != null) {
this.leftNode.infixOrder();
}
System.out.println(this);
if (this.rightNode != null) {
this.rightNode.infixOrder();
}
}
// Postorder traversal
public void postOrder() {
if (this.leftNode != null) {
this.leftNode.postOrder();
}
if (this.rightNode != null) {
this.rightNode.postOrder();
}
System.out.println(this);
}
// Preorder search
public heroNode PreOrderSearch(int no) {
System.out.println("Preorder search");
//Compare whether the no of the current node is what we want to search
if (this.id == no) {
return this;
}
//Node to return
heroNode resNode = null;
// Judge whether the node on the left is empty. If it is not empty, recursive preamble search is performed
// If found, return the found node
if (this.leftNode != null) {
resNode = this.leftNode.PreOrderSearch(no);
}
//If it is not null, it means that if it is found on the left, it can be returned directly
if (resNode != null) {
return resNode;
}
// Judge whether the node on the right is empty. If it is not empty, recursive preamble search is performed
// If found, return the found node
if (this.rightNode != null) {
resNode = this.rightNode.PreOrderSearch(no);
}
return resNode;
}
// Medium order search
public heroNode infixOrderSearch(int no) {
//Node to return
heroNode resNode = null;
// Judge whether the left node is empty. If it is not empty, search in recursive order
// If found, return the found node
if (this.leftNode != null) {
resNode = this.leftNode.infixOrderSearch(no);
}
//If it is not null, it means that if it is found on the left, it can be returned directly
if (resNode != null) {
return resNode;
}
//Compare whether the no of the current node is what we want to search
System.out.println("Medium order search");
if (this.id == no) {
return this;
}
// Judge whether the node on the right is empty. If it is not empty, search in recursive order
// If the node is found, it will return
if (this.rightNode != null) {
resNode = this.rightNode.infixOrderSearch(no);
}
return resNode;
}
// Sequential search
public heroNode postOrderSearch(int no) {
//Node to return
heroNode resNode = null;
// Judge whether the node on the left is empty. If it is not empty, it will be searched recursively
// If found, return the found node
if (this.leftNode != null) {
resNode = this.leftNode.postOrderSearch(no);
}
//If it is not null, it means that if it is found on the left, it can be returned directly
if (resNode != null) {
return resNode;
}
// Judge whether the node on the right is empty. If it is not empty, it will be searched recursively
// If found, return the found node
if (this.rightNode != null) {
resNode = this.rightNode.postOrderSearch(no);
}
//If it is not null, it means that if it is found on the right, it can be returned directly
if (resNode != null) {
return resNode;
}
System.out.println("Sequential search");
//If the left and right subtrees are not found, then compare whether the no of the current node is what we want to search
if (this.id == no) {
return this;
}
return resNode;
}
// delete
public void deleteNode(int no) {
// Traverse to the left. If the left subtree is a little, set the left subtree empty. If not, traverse the right
if (this.leftNode != null && this.leftNode.id == no) {
this.leftNode = null;
return;
}
// Traverse to the right. If the right subtree is a little, set the left subtree empty. If there is no ready left or right, it should be deleted recursively
if (this.rightNode != null && this.rightNode.id == no) {
this.rightNode = null;
return;
}
// If the above two steps are unsuccessful, let's delete recursively to the left first
if (this.leftNode != null) {
this.leftNode.deleteNode(no);
}
// If the recursive deletion of the left subtree is not successful, the right subtree will be deleted recursively
if (this.rightNode != null) {
this.rightNode.deleteNode(no);
}
}
}