preface:
- This paper introduces the recursive and non recursive algorithms of traversal, among which the non recursive algorithm of post order traversal is the most difficult.
- Questions included by bloggers: New Young
- Please indicate the source of Reprint: New Young
Mind map
[the external chain picture transfer fails, and the source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-voghesek-1645797380622) (% E9% 81% 8D% E5% 8e% 86. Assets / 202252155405. PNG)]
proposal
- Binary tree is a recursive structure!!!!!!!!!, This must always be borne in mind.
- Recursion uses the idea of division and autonomy, which is very convenient to solve the binary tree problem
- Recursion we generally recommend to judge the false situation first, which will be very easy to solve the problem.
- When using recursion, if you can't complete all the code at once, you can complete the general part first, and then slowly fill in the details.
Recursive 3 elements
- Use of return value of recursive function
- Parameter setting of recursive function
- The judgment of the end condition of recursion.
Traversal of binary tree
Traversal means: print the value of each node in a binary tree, but because there are left and right subtrees, there are four kinds of traversal of binary tree: pre order traversal, middle order traversal, post order traversal and sequence traversal
PS:
- For empty nodes, NULL is printed by default for easy viewing.
- Traversal can only traverse the current tree to traverse other upper level trees or brother level trees.
Preorder traversal
It is required to print the value of the root node before traversing the left and right subtrees of the binary tree, and then traverse the right subtree after traversing the left subtree.
Abbreviation: root left right
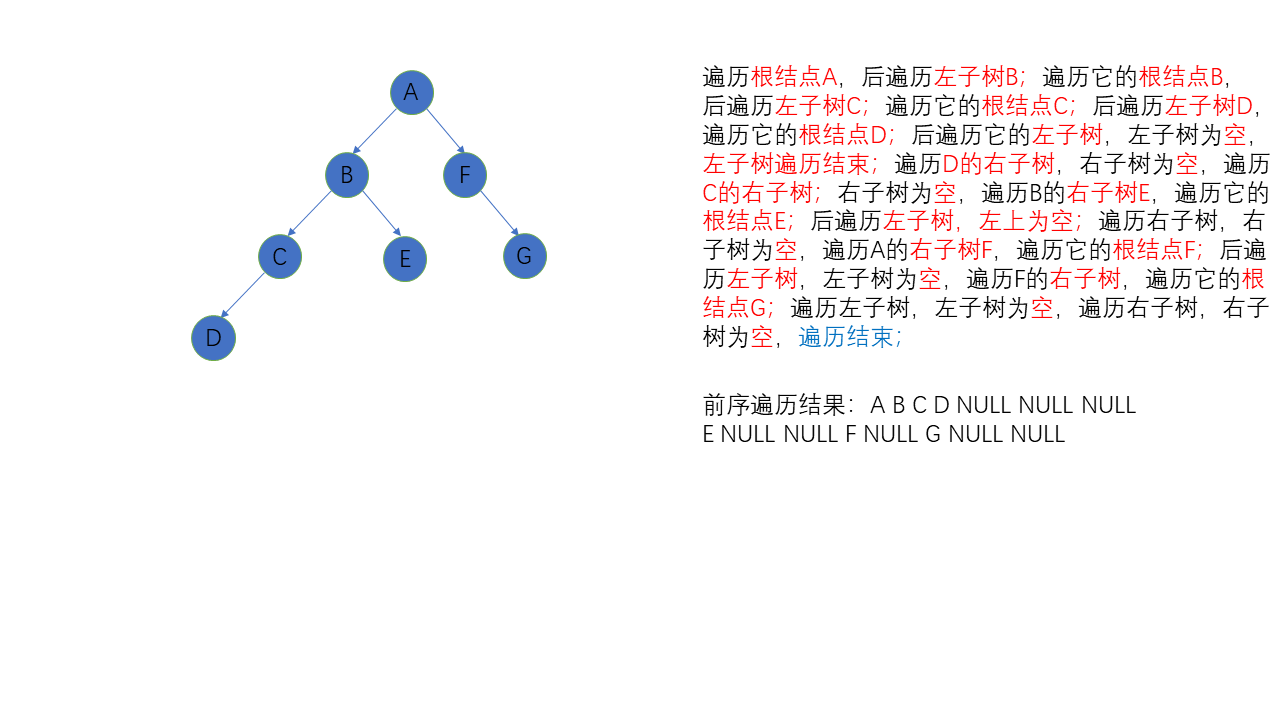
recursion
thinking
[the external chain picture transfer fails. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-eebw1k5y-1645797380638) (% E9% 81% 8D% E5% 8e% 86. Assets / image-20220225162701635-1645776228533. PNG)]
Based on three elements:
-
The preorder traversal function does not need to return a value, so void
-
Parameter, only one pointer is needed, so
void PreOrder(BTNode* root);// Preorder traversal of binary tree -- recursive method
3. Ending conditions:
if(root==NULL)
{
printf("NULL ");
return ;
}
- traversal order
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right)
Complete code
//Preorder traversal is to visit the root node of the binary tree before the left and right children.
void PreOrder(BTNode* root)
{
if(root==NULL)
{
printf("NULL ");
return ;
}
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
non-recursive
thinking
We know that the function stack frame occurs in the stack area, and the characteristics of this stack area (first in, then out, first with low address and then with high address) are the same as the stack in the data structure. Therefore, here we can simulate the stack area of the function stack frame through the stack of the data structure.
- First of all, because of the characteristics of the stack - first in first out, the left subtree must be accessed first. Therefore, we first store the address of the right subtree in the array stack, and then store the left subtree in the array stack.
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-dpqcyn7d-1645797380639) (% E9% 81% 8D% E5% 8e% 86. Assets / 202252053310. PNG)]
code
void PreOrderNoR(BTNode* root)// Preorder traversal of binary tree -- non recursive method
{
assert(root);
stack st;
StackInit(&st);
//We need a root node to enter the right subtree, so we need a stub node
//At the same time, once the left subtree is accessed, the root node is required when entering the right subtree, but not later. So pop
SDateType p = root;
while (1)
{
if (p != NULL)
{
printf("%c->", p->data);
StackPush(&st, p);
p = p->left;
}
else
{
printf("NULL->");
break;
}
}
while (!StackEmpty(&st)||p)//An empty tree or stack ends empty
{
/
//p is empty, indicating that the root and left subtree are traversed.
if (!StackEmpty(&st))
{
p = StackTop(&st);
StackPop(&st);
p = p->right;
while (1)
{
if (p != NULL)
{
printf("%c->", p->data);
StackPush(&st, p);
p = p->left;
}
else
{
printf("NULL->");
break;
}
}
}
}
printf("\n");
StackDestroy(&st);
}
Middle order traversal
Before accessing the root node, first access the left subtree. When the left subtree is empty, then access the root node, and then access the right subtree.
Introduction: left – root – right
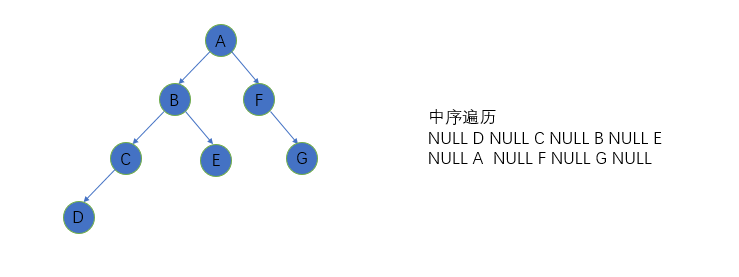
recursion
thinking
Similar to the previous traversal, the left subtree needs to be recursive before accessing the root node.
code
void InOrder(BTNode* root)// Order traversal in binary tree
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
non-recursive
thinking
Also use the stack to simulate the stack area.
However, the address of the left subtree should be stored in the array stack first. When the empty tree is stored, you can access the root node, and then traverse the right subtree and repeat the process.
code
void InOrderNoR(BTNode* root)// Order traversal in binary tree -- recursive method
{
assert(root);
stack st;
StackInit(&st);
//We need a root node to enter the right subtree, so we need a stub
SDateType p = root;
//Traverse to the lowest end of the left subtree
while (1)
{
if (p != NULL)
{
StackPush(&st, p);
p = p->left;
}
else
{
printf("NULL->");
break;
}
}
while (!StackEmpty(&st) || p)//An empty tree or stack ends empty
{
if (!StackEmpty(&st))
{
SDateType tmp= StackTop(&st);
printf("%c->", tmp->data);
StackPop(&st);
p = tmp->right;
//The root node has traversed the game ratio, and it is not needed for subsequent traversal.
//No matter whether the right subtree is empty or not, the root node is not required even if it comes back.
//Traverse to the lowest end of the left subtree
while (1)
{
if (p != NULL)
{
StackPush(&st, p);
p = p->left;
}
else
{
printf("NULL->");
break;
}
}
}
}
printf("\n");
StackDestroy(&st);
}
Postorder traversal
Before accessing the root node, the left and right subtrees must be accessed before accessing the root node.
Abbreviation: left right root
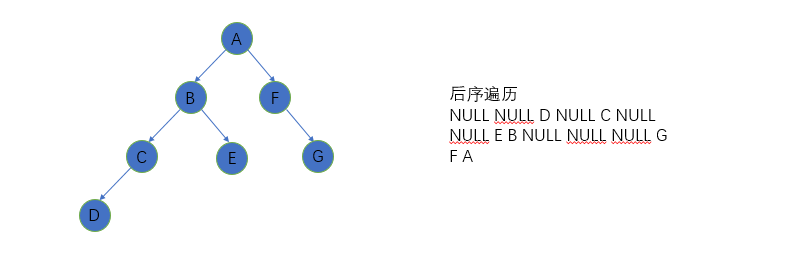
recursion
thinking
Similar to the previous sequence, it only needs to end the left and right access first, and then access the root node
code
void PostOrder(BTNode* root)// Postorder traversal of binary tree
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}
non-recursive
thinking
1. The root node can be accessed only after the left and right subtrees are accessed.
Therefore, there should be a pVisist pointer to record the accessed left or right subtree. When pvisit = P - > right|p - > right = = null, access the root node.
2. When we visit the existing right subtree, we still regard it as a binary tree, so we still need to press and out of the stack,
3. Here I print NULL to help better understand,
code
void PostOrderNoR(BTNode* root)// Post order traversal of binary tree -- non recursive method
{
//Idea: 1 The root node can be accessed only after the left and right subtrees are accessed.
// Therefore, there should be a pVisist pointer to record the accessed left or right subtree. When pvisit = P - > right|p - > right = = null, access the root node.
// 2. When we visit the existing right subtree, we still regard it as a binary tree, so we still need to press and out of the stack,
// 3. Here I print NULL to help better understand,
assert(root);
assert(root);
stack st;
StackInit(&st);
SDateType p = root;
SDateType pVisit = NULL;//Mark left and right subtrees
//Simplified version - only assign Top to p, but note that when the right subtree is not empty, you must directly stack the left subtree. Because the value of p is not empty.
while (1)//First stack the left subtree. When the left subtree is empty, start accessing the right subtree.
{
if (p == NULL)
{
printf("NULL->");
break;
}
else
{
StackPush(&st, p);
p = p->left;
}
}
while (!StackEmpty(&st) || p)//An empty tree or stack ends empty
{
if (!StackEmpty(&st))
{
p = StackTop(&st);
//Only when the right subtree is empty or the right subtree has been accessed can the root node be accessed and the root node be deleted
if (p->right == NULL || p->right == pVisit)
{
if (p->right == NULL)
{
printf("NULL->");
}
StackPop(&st);
printf("%c->", p->data);
pVisit = p;
//This part indicates that the subtree has been accessed, but it is not really a left subtree or a right subtree. Therefore, P - > right = = pvisit is required
}
else
{
p = p->right;//The next loop will be the traversal of the right subtree.
while (1)
{
if (p == NULL)
{
printf("NULL->");
break;
}
else
{
StackPush(&st, p);
p = p->left;
}
}
}
}
}
printf("\n");
StackDestroy(&st);
}
level traversal
- Sequence traversal is different from the former, middle and later. It requires that the nodes of the first layer of the tree must be traversed before traversing the next layer.
- Sequence traversal uses queues to achieve sequence traversal.
- Note that due to the characteristics of the queue (first in, first out), the left subtree needs to enter the queue first.
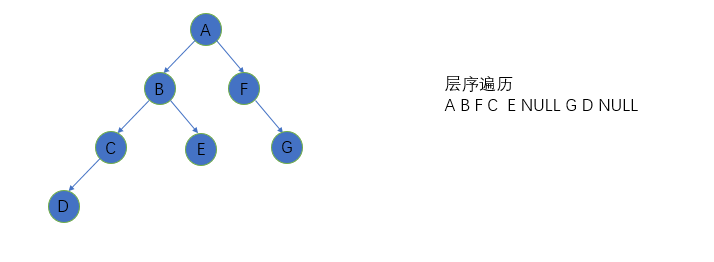
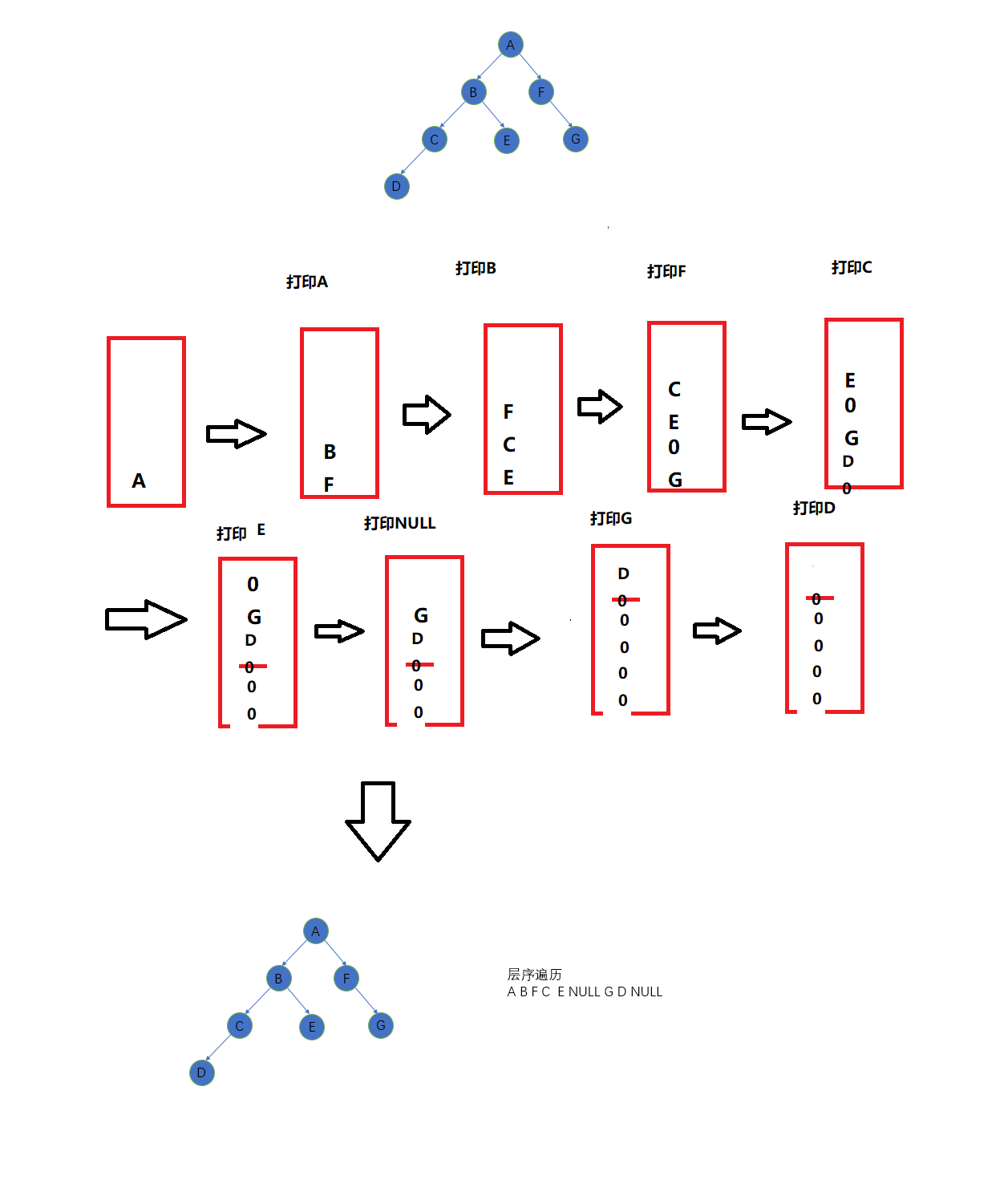
code
void LevelOrder(BTNode* root)// level traversal
{
if (root == NULL)
{
return;
}
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* tmp = QueueTop(&q);
printf("%c ", tmp->data);
QueuePop(&q);
if (tmp->left != NULL)
{
QueuePush(&q, tmp->left);
}
if (tmp->right != NULL)
{
QueuePush(&q, tmp->right);
}
}
QueueDestroy(&q);
}