introduce
My LeetCode homepage, one problem one solution
Tags: queue, dynamic programming, binary search
363. The rectangular area does not exceed the maximum value of K and
Difficulty difficulty
subject
Give you a matrix of m x n and an integer k, find out and return the maximum sum of values not exceeding K in the rectangular area inside the matrix.
The title data ensures that there will always be a rectangular area with a value and no more than k.
Example 1:
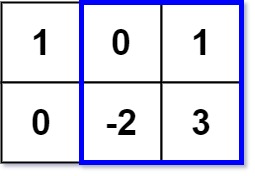
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: the sum of the values of the rectangular area [[0,1], [- 2,3]] circled by the blue border is 2, and 2 is the maximum number not exceeding K (k = 2).
Example 2:
Input: matrix = [[2,2,-1]], k = 3
Output: 3
Tips:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -100 <= matrix[i][j] <= 100
- -105 <= k <= 105
Advanced: how to design a solution if the number of rows is much larger than the number of columns?
Understand the topic
The title gives a matrix and an integer k
Among them, we need a sub matrix, which meets the following requirements:
- Where the sum of elements is less than K
- Not only should it be less than k, but also all the matrices that satisfy the element and maximum of condition one
Analysis topic
Through the analysis of the problem, we can see that the prefix and can be used to solve this problem
Why do you think so? Because I've done it before 304. Two dimensional area and retrieval - matrix immutable (my problem solution)
It is also a rectangle to calculate the area. In this way, the operation time can be reduced by prefix and
If the traversal problem 304 can be used directly
Here I define two coordinate points of the submatrix for later explanation
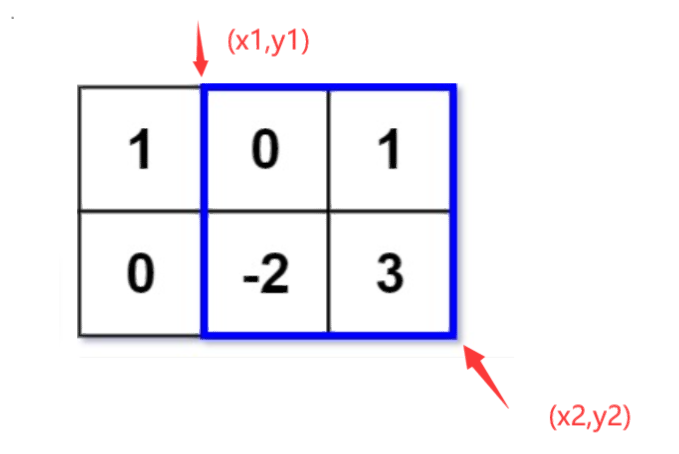
Since you want to use prefix and, you always need to initialize first
That is, calculate the sum of the elements of each submatrix when (x1,y1) is (0,0)
int[][] sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1]
- sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
Naive prefix and
Directly use 4-fold loop to traverse each sub matrix. The time complexity is O (m ^ 2 * n ^ 2), but it will probably time out, so it only means
// Pointing submatrix x1
for (int i = 1; i <= m; i++) {
// y1 pointing to submatrix
for (int j = 1; j <= n; j++) {
// x2 pointing to submatrix
for (int p = i; p <= m; p++) {
// y2 pointing to submatrix
for (int q = j; q <= n; q++) {
// Quadruple cyclic ergodic submatrix
}
}
}
}
Prefix and + dichotomy
Using TreeSet ceiling()
The submatrix corresponds to four edges. When we fix three of them, can we get the last one in a simpler way?
The main problem is that there are elements with negative weight, which destroys the order of the array, and the use of dichotomy is not very reasonable
So is there a solution?
The results are given directly here. To see the derivation process, please see Teacher Miyazawa Sanya's explanation
- Use TreeSet to maintain all right boundaries traversed
- Use the ceiling() method to return the smallest element greater than or equal to the given element
- If it exists, give two points
- If it doesn't exist, go back
- In conclusion, this method first traverses to obtain the right boundary, and then looks for the value that can become the left boundary in the traversed boundary
- Optimization is to use TreeSet, an ordered set based on red and black trees, so that the acquisition time of the last edge is O(log n)
Here is a picture of Mr. Miyoshi Sanye:
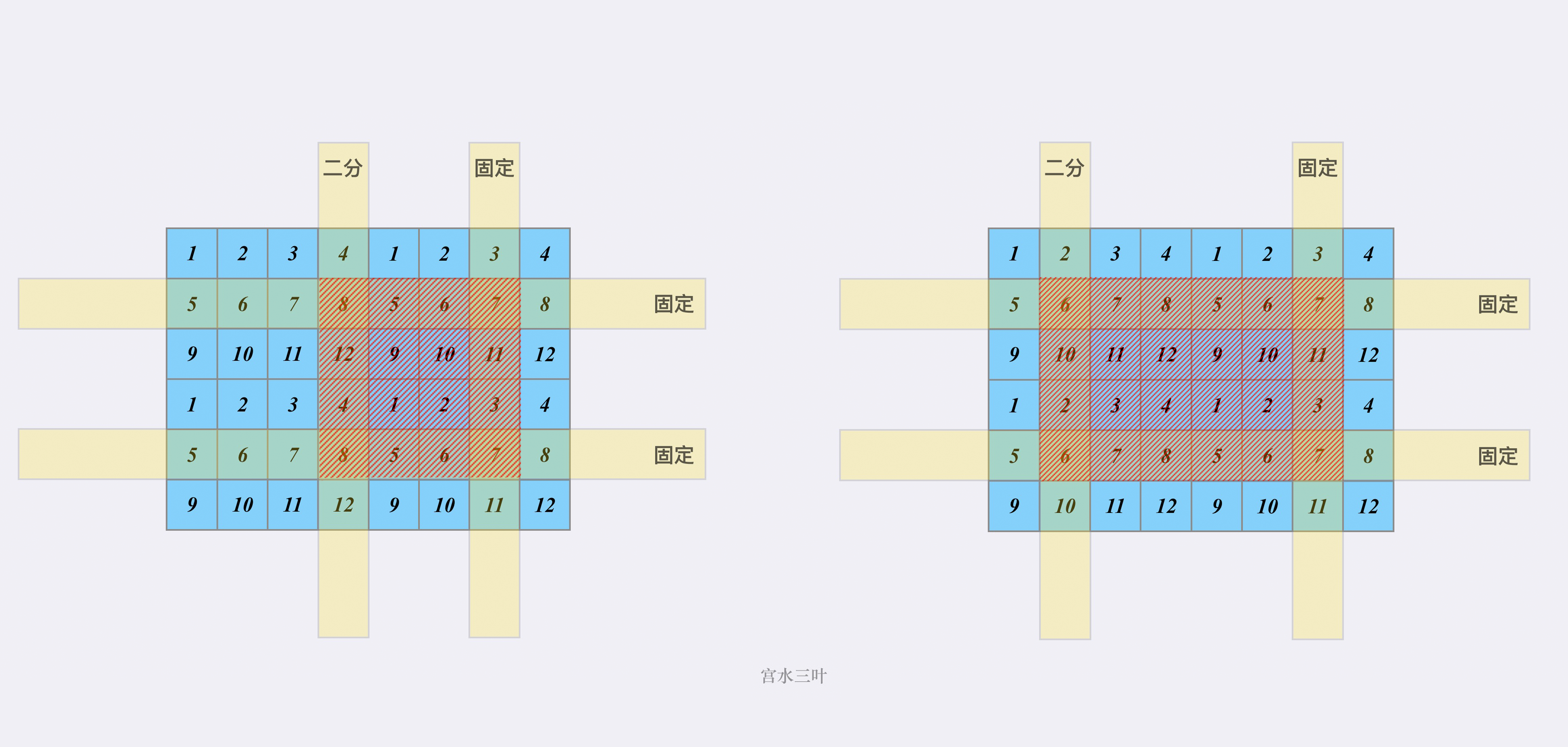
In the figure, it means to fix the upper, lower and right boundaries, and binary search the left boundary
Corresponding code
This code is the first version of Ms. Miyoshi Sanye's code. For the optimized version, please also see Ms. Miyoshi Sanye's problem solution
class Solution {
public int maxSumSubmatrix(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
// Preprocessing prefix and
int[][] sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
int ans = Integer.MIN_VALUE;
// Upper boundary of ergodic submatrix
for (int top = 1; top <= m; top++) {
// Ergodic lower boundary of submatrix
for (int bot = top; bot <= m; bot++) {
// Use "ordered set" to maintain all right boundaries traversed
TreeSet<Integer> ts = new TreeSet<>();
// Add an initial value to the ordered set
ts.add(0);
// Ergodic right boundary of submatrix
for (int r = 1; r <= n; r++) {
// Calculate right by prefix and
int right = sum[bot][r] - sum[top - 1][r];
// Find left by two points
Integer left = ts.ceiling(right - k);
if (left != null) {
// If left exists, it means that the dichotomy has a left boundary that meets the conditions. At this time, the result is updated
int cur = right - left;
ans = Math.max(ans, cur);
}
// Add the traversed right to the ordered set
ts.add(right);
}
}
}
return ans;
}
}

Using auxiliary arrays
- Fix the left and right boundaries (of course, fixing the upper and lower boundaries is the same)
- Set up the auxiliary array rowSum [], which stores the matrix elements and of each row between the two boundaries
Here I borrow lzhlyle's picture

It should be clear at this time:
The sum of rowSum continuous subarrays is the sum of rectangular elements corresponding to the upper and lower boundaries
At this time, the problem is to find the maximum subarray of elements and less than k in rowSum []
-
Double loop Traversal Solution
-
reference 53. Maximum subsequence sum Solution in:
public int maxSubArray(int[] nums) { int len = nums.length, max, dp; if (len == 0) return 0; // To be as big as possible, try not to be negative dp = max = nums[0]; for (int i = 1; i < len; i++) { // The previous and are smaller than the current ones. What else should we do dp = Math.max(dp, dp + nums[i]); // Update max max = Math.max(max, dp); } return max; }
At this time, analyze the relationship between the returned max and k:
-
If Max is still less than k, it will be directly updated to the final result: res = math max(max, res);
-
If max is larger than k, then traverse rowSum [], and update all traversed results less than k to res
for (int a = 0; a < row; a++) { int currSum = 0; for (int b = a; b < row; b++) { currSum += sum[b]; if (currSum <= k) res = Math.max(currSum, res); } }
Corresponding code
class Solution {
public int maxSumSubmatrix(int[][] matrix, int k) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return 0;
int row = matrix.length;
int col = matrix[0].length;
int res = Integer.MIN_VALUE;
// Fixed left and right boundaries
for (int i = 0; i < col; i++) {// Enumeration left boundary
int[] sum = new int[row];
for (int j = i; j < col; j++) {// Enumeration right boundary
// Sum only for rows
for (int r = 0; r < row; r++) {
sum[r] += matrix[r][j];
}
int dp = 0;
int max = sum[0];
for (int n : sum) {
// The previous and are smaller than the current ones. What else should we do
dp = Math.max(n, dp + n);
// Update max
max = Math.max(dp, max);
// If the maximum is found to be k, return k directly
if (max == k)
return max;
}
if (max < k) {
res = Math.max(max, res);
}
else {
for (int a = 0; a < row; a++) {
int currSum = 0;
for (int b = a; b < row; b++) {
currSum += sum[b];
if (currSum <= k)
res = Math.max(currSum, res);
}
}
// If the maximum is found to be k, return k directly
if (res == k) return res;
}
}
}
return res;
}
}

Thank you for your reference:
Teacher lzhlyle's Java, optimize from violence, with drawings and notes
Miss Miyazawa Sanya's The basic idea of optimizing enumeration & abstracting two dimensions into one dimension & maximizing "dichotomy" benefits & spatial optimization