Accurate values of arithmetic, factorial, twin prime numbers, 6174 problems for pupils

Preface 🍀

Today, I'll share with you some of the algorithmic problems I brushed up about numerical processing. Although the topic is relatively simple, the way in which the problem is handled is worth learning. Pupil arithmetic involves addition carry, factorial exact values used to calculate a number that results in a very long time, twin prime numbers are two adjacent prime numbers (simpler), 6174 problems can be simulated according to the title.

Primary Arithmetic 🗽

🗽 Problem Description

Recently, many pupils have come to the first quiz of Quick School. Pupils can be embarrassed when they enter the additive level.
Because if you don't pay attention to the rounding, you will make a mistake. Please design a program to calculate the addition of two digits
How many rounds are needed for pupils to check whether they are in the correct rounds. (ends with 0)
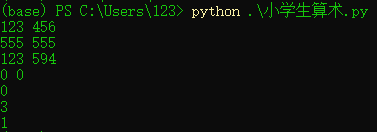
Sample input:
123 456
555 555
123 594
0 0
Sample output: 0
3
1

🗽 problem analysis

You can set a flag point to determine whether two numbers need to be rounded when calculating.
Set the advanced flag digit value to 1 if it is rounded, or 0 if it is not rounded
This is because the carry-up is 1 in addition. 9+9=18, leaving 8 to take 1 higher

🗽 code implementation

Old Rules First Run Result:

Add code:

import sys
flag=0
lis=[]
num=0
while True:
    m,n=sys.stdin.readline().strip().split()
    m,n=int(m),int(n)
    if n==m==0:
        break
    # The loop terminates as long as m,n is transformed to have a value of 0
    while m and n:
        if (m%10+n%10+flag)>=10:
            num+=1
            flag=1
        else:
            flag=0
        m//=10
        n//=10
    lis.append(num)
    num=0
for i in lis:
    print(i)

Factorial exact value 🐳

🐳 Problem Description

It is well known that the number of digits in a Python numeric type is related to the memory of the computer. It's easy to implement the factorial of n
However, for C, C++, integers have a certain length of digits. Overflow over a certain length
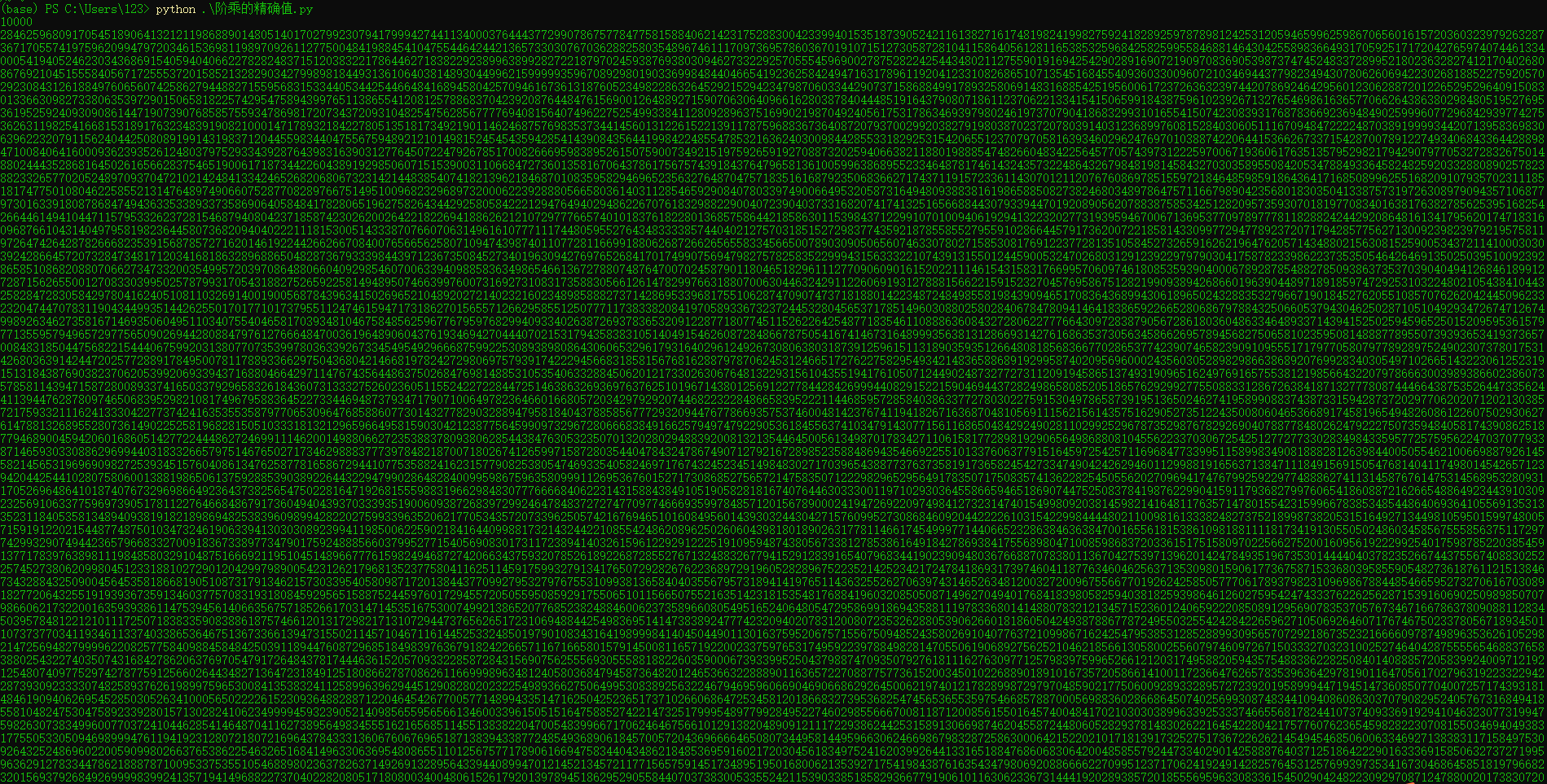
Enter no more than 1000 positive integers n, output n!= The exact result of 1234...*n.
Sample input: 30
Sample output: 2652859812191058636308480000000

🐳 problem analysis

Very long calculations don't have much impact on the Python language, because Pyhton determines the size of the integer based on the size of the computer's memory. For languages like C\C++, numeric types have a certain length. Overflow beyond a certain length will affect the final result. For this topic, we need to use arrays to store the results of calculation and then simulate multiplication by ourselves. The result of calculation is obtained.

🐳 code implementation

Old Rules First Run Result:

Top Code:
There are two methods used here, one is direct calculation, the other is analogue multiplication using the C language style.
Python's built-in modules are powerful, direct computing is super convenient, and can calculate very long numbers in very little time
(Fig. below) But if we're looking for something to do for ourselves today, we'll use Pyhton to simulate the C language.

Even though calculating the factorial of 10,000 takes less than seconds

import time
def timmer(func):
    def weapper(*s):
        start=time.time()
        func(*s)
        end=time.time()
        print("Time-consuming:",end-start)
    return weapper

@timmer
def f1(n):
    # Direct calculation
    ans=1
    # Number of digits to mark where it is now
    if n==0 or n==1:
        print(1)
        exit()
    else:
        for i in range(2,n+1):
            ans=ans*i
                
    print(ans)
@timmer
def f2(n):
    # C Language Method Precise Calculation
    ans=[0]*1000
    ans[0]=1
    for i in range(2,n+1):
        j=0
        c=0
        while j<1000:
            temp=ans[j]*i+c
            ans[j]=temp%10
            c=temp//10
            j+=1

    i=len(ans)-1
    flag=True
    while i>=0:
        if flag and ans[i]==0:
            pass
        else:
            print(ans[i],end="")
            flag=False
        i-=1
    print()

if __name__=="__main__":
    n=int(input())
    # f1(n)
    f2(n)

Twin prime numbers 🛸

🛸 Problem Description

A prime number, also known as a prime number, is an integer that can only be divided by one and itself, and greater than one gives a number, a twin prime number smaller than him
A twin prime number means two consecutive prime numbers next to each other, with a difference of 2 (that is, N and n-2)
Now give a positive integer, calculate the two nearest twin prime numbers smaller than him.
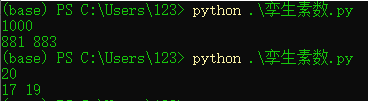
Sample input: 1000
Sample output: 881 883

🛸 problem analysis

To determine if it is a twin prime number, the first step is to determine if it is a prime number. Yes, then judge if the number differs by 2 from it is a prime number.
If both are output directly, otherwise continue judging.

🛸 code implementation

Old Rules First Run Result:

Top Code:

def is_ok(num):
    if num==1:
        return False
    for i in range(2,int(math.sqrt(num))+1):
        if num%i==0:
            return False
    return True


n=int(input())
while n:
    if is_ok(n) and is_ok(n-2):
        print(n-2,n)
        break
    n-=1

6174 Question 🎱

🎱 Problem Description

Suppose you have four digits with different numbers. Sort the numbers in this number from large to small to get a
Sort from smallest to largest to get b, then use a-b to get the result instead of the original number. And continue with the same operation.
Task: Enter a number n to output a sequence of operations. Until a loop occurs, such as 6174 before sorting, the result is also 6174
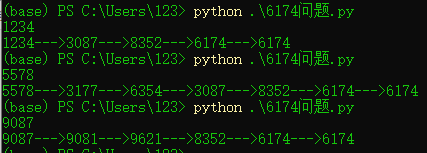
Sample input: 1234
Sample output: 1234->3087->8352->6174->6174

🎱 problem analysis

Involves sorting numbers in numbers
After sorting, use large minus small, and then compare the results with the original number.

🎱 code implementation