💟 Author's introduction: Hello, my name is Ceylan_, Can call me CC ❣️ *
📝 Personal home page: Ceylan_ Blog
🏆 Blogger information: ordinary freshmen have extraordinary dreams
Columns
⚡ I hope you can support me a lot 😘 Progress Together~ ❤️
🌈 If it helps, please pay attention ➕ Give the thumbs-up ➕ Collection], if not, I will work hard again 💪
Catalog
🌸 High Precision Multiplication
🌸 Preface
Let's look at a topic like this
Calculates the sum of 356441531584213921368 and 5984526842352952356, minus, multiply, divide
When such numbers need to be added, subtracted, multiplied, and divided, the traditional method will exceed the range of data sizes that can be represented by standard data types. So what should I do?

High precision algorithms are needed here.
🌸 What is high precision?
High-precision algorithms are mathematical computational methods for processing large numbers. In the calculation, the number may be hundreds of billions of large numbers. In general, such numbers are collectively referred to as high-precision numbers. When calculating high-precision numbers, it is obvious that the general method cannot be used.
 What shall I do?
What shall I do?
We can use arrays to store large numbers one by one, and elementary school vertical thinking to achieve high-precision arithmetic operations, for example
234+567
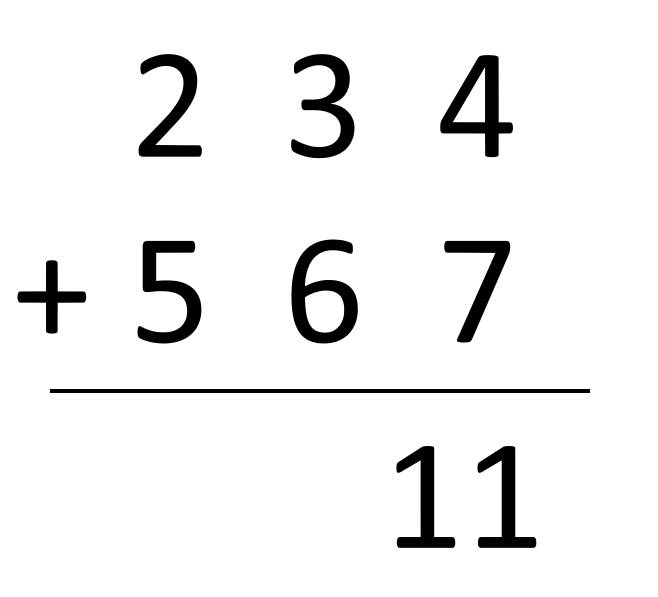
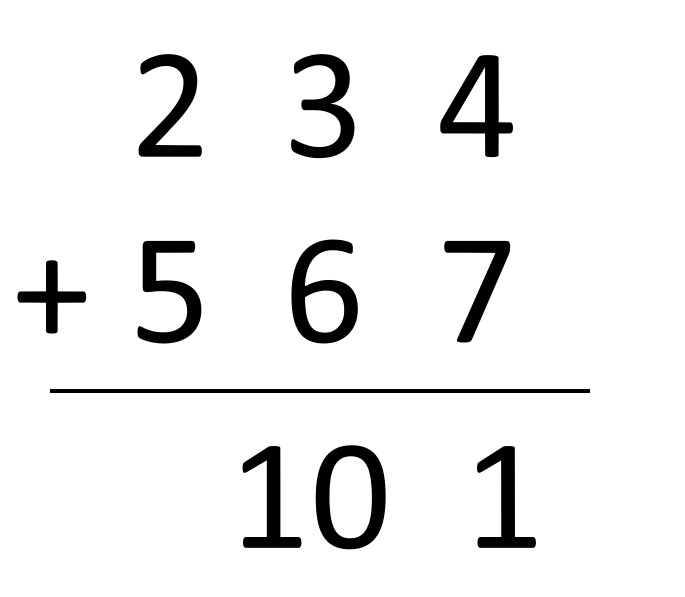
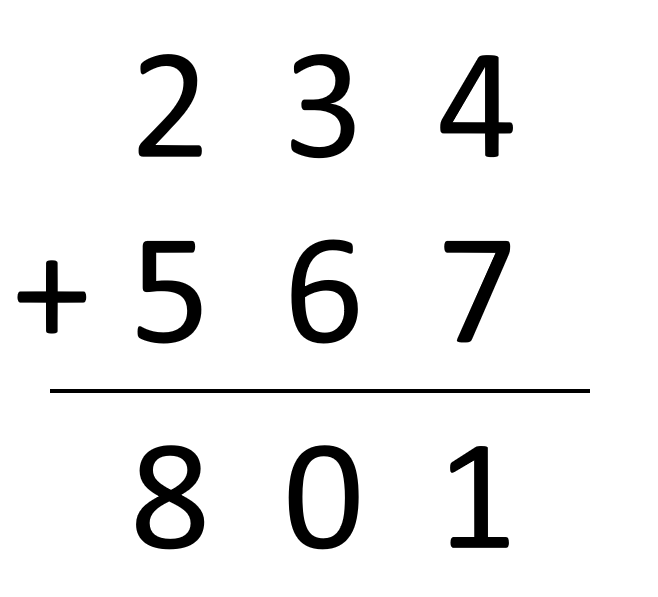
We calculate the sum of each bitwise two terms separately. If the result is greater than 10, the first bitwise one goes on until the result is obtained.
To summarize, there are several steps to implement high precision algorithms:
1 ️⃣ Store each bit of a high precision number in an array separately
2 ️⃣ Calculate the same bit result
3 ️⃣ Or if the result is greater than 10, move forward one item, and if the result is less than 10, leave it unchanged
4 ️⃣ Continue calculating the next bit until the end of the operation
🌸 High Precision Addition
💬 Code demonstration
#include<iostream>
#include<cstring>
using namespace std;
int main()
{
string str1,str2;
int a[250],b[250],len1,len2,len;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
cin>>str1>>str2;
len1=str1.size();
len2=str2.size();
for(int i=0;i<=len1;i++)
{
a[i]=str1[len1-i]-'0';
}
for(int i=0;i<=len2;i++)
{
b[i]=str2[len2-i]-'0';
}
len=max(len1,len2);
for(int i=1;i<=len;i++)
{
a[i]+=b[i];
a[i+1]+=a[i]/10;
a[i]%=10;
}
len++;
while((a[len]==0)&&(len>1)) len--;
for(int i=len;i>=1;i--)
cout<<a[i];
return 0;
}🌸 High Precision Subtraction
💬 Code demonstration
#include<iostream>
#include<cstring>
using namespace std;
int compare(string s1,string s2);
int main()
{
string str1,str2;
int a[250],b[250],len1,len2;
int i;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
cin>>str1>>str2;
len1=str1.length();
for(i=1;i<=len1;i++)
a[i]=str1[len1-i]-'0';
len2=str2.length();
for(i=1;i<=len2;i++)
b[i]=str2[len2-i]-'0';
if((compare(str1,str2))==0)
{
for(i=1;i<=len1;i++)
{
a[i]-=b[i];
if (a[i]<0)
{
a[i+1]--;
a[i]+=10;
}
}
len1++;
while((a[len1]==0)&&(len1>1))
len1--;
for(i=len1;i>=1;i--)
cout<<a[i];
cout<<endl;
}
else
{
cout<<'-';
for(i=1;i<=len2;i++)
{
b[i]-=a[i];
if (b[i]<0)
{
b[i+1]--;
b[i]+=10;
}
}
b[0]++;
while((b[len2]==0)&&(len2>1))
len2--;
for(i=len2;i>=1;i--)
cout<<b[i];
cout<<endl;
}
return 0;
}
int compare(string s1,string s2)
{
if(s1.length()>s2.length()) return 0;
if(s1.length()<s2.length()) return 1;
for(int i=0;i<=s1.length();i++)
{
if(s1[i]>s2[i]) return 0;
if(s1[i]<s2[i]) return 1;
}
return 0;
} 🌸 High Precision Multiplication
💬 Code demonstration
#include<iostream>
#include<cstring>
using namespace std;
int main()
{
string str1,str2;
int a[250],b[250],c[250],len1,len2,len;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
cin>>str1>>str2;
len1=str1.size();
len2=str2.size();
for(int i=0;i<=len1;i++)
{
a[i]=str1[len1-i]-'0';
}
for(int i=0;i<=len2;i++)
{
b[i]=str2[len2-i]-'0';
}
for(int i=1;i<=len1;i++)
{
for(int j=1;j<=len2;j++)
{
c[i+j-1]+=a[i]*b[j];
c[i+j]+=c[i+j-1]/10;
c[i+j-1]%=10;
}
}
len=len1+len2+1;
while((c[len]==0)&&(len>1)) len--;
for(int i=len;i>=1;i--)
cout<<c[i];
return 0;
}🌸 High Precision Division
💬 Code demonstration
Even an immature attempt is better than a strategy in a stillborn baby.
🌺 Daily Golden Sentences
Even an immature attempt is better than a strategy in a stillborn baby.

I am not a talented person. If there are any mistakes, you guys are welcome to correct them in the comments area. If it's helpful, please pay attention ➕ Give the thumbs-up ➕ Collection], if not, I will work hard again 💪💪💪
