GitHub sync update (Classified): Data_Structure_And_Algorithm-Review (it's best to give a star!!!)
The following is the main body of this article, and the following cases can be used for reference.
What is Huffman tree?
Given N weights as N leaf nodes, a binary tree is constructed. If the weighted path length of the tree reaches the minimum, such a binary tree is called the optimal binary tree, also known as Huffman tree.
Huffman tree is the tree with the shortest weighted path length, and the node with large weight (which can be understood as the probability of occurrence) is closer to the root.
(Baidu Encyclopedia)
Overview of Huffman tree
1). Huffman tree
For example, see what problems Huffman trees can solve.
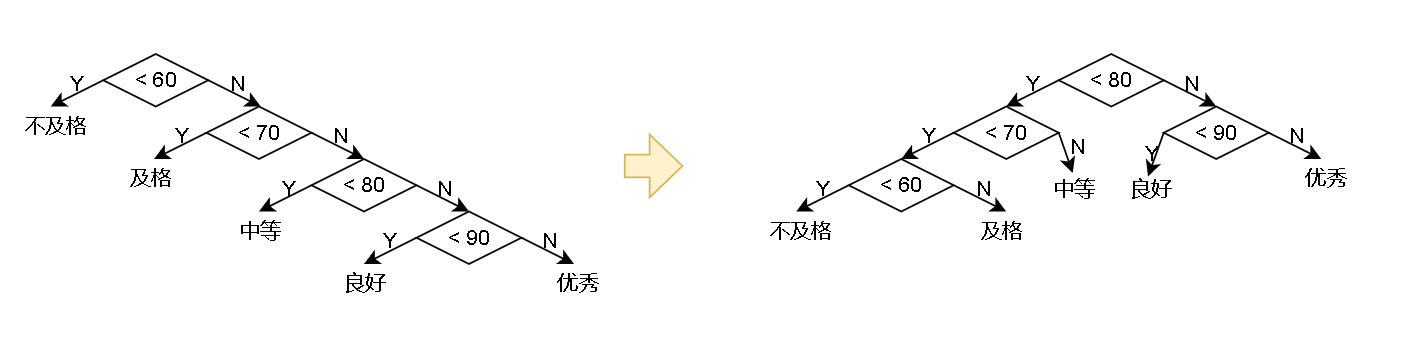
For example, change the grade of a class from the hundred mark system to the grade system (100 people).
Someone might write code like this:
if(score < 60){
cout<<"fail,"<<endl;
}else if(score < 70){
cout<<"pass"<<endl;
}else if(score < 80){
cout<<"secondary"<<endl;
}else if(score < 90){
cout<<"good"<<endl;
}else{
cout<<"excellent"<<endl;
}
It's really no problem to write this, but it's not necessarily the number of judgments.
For example, the results of this class obey the normal distribution, and the probabilities of the five grades are
10
%
,
20
%
,
40
%
,
20
%
,
10
%
10\%,20\%,40\%,20\%,10\%
10%,20%,40%,20%,10%
Let's calculate. We need to judge:
100
×
10
%
×
1
+
100
×
20
%
×
2
+
100
×
40
%
×
3
+
100
×
20
%
×
4
+
100
×
10
%
×
5
=
300
second
one hundred × 10\% × 1 + 100 × 20\% × 2 + 100 × 40\% × 3 + 100 × 20\% × 4 +100 × 10\% × 5 = 300 times
one hundred × 10% × 1+100 × 20% × 2+100 × 40% × 3+100 × 20% × 4+100 × 10% × 5 = 300 times
When we first judge the group with the greatest probability:
if(score < 80){
if(score < 70){
if(score < 60){
cout<<"fail,"<<endl;
}else{
cout<<"pass"<<endl;
}
}else{
cout<<"secondary"<<endl;
}
}else if(score < 90){
cout<<"good"<<endl;
}else{
cout<<"excellent"<<endl;
}
Let's calculate. We need to judge:
100
×
40
%
×
2
+
100
×
20
%
×
2
+
100
×
10
%
×
2
+
100
×
20
%
×
3
+
100
×
10
%
×
3
=
230
second
one hundred × 40\% × 2 + 100 × 20\% × 2 + 100 × 10\% × 2 + 100 × 20\% × 3 + 100 × 10\% × 3 = 230 times
one hundred × 40% × 2+100 × 20% × 2+100 × 10% × 2+100 × 20% × 3+100 × 10% × 3 = 230 times
2). Huffman coding
In 1952, mathematician D.A.Huffman proposed the best coding method of using the frequency of characters in the file (0, 1 string) to represent each character, which is called Huffman coding.
Huffman coding solves the above problems well and is widely used in data compression, especially in long-distance communication and high-capacity data storage. The commonly used JPEG pictures are compressed by Huffman coding.
The basic idea of Huffman coding is to construct a Huffman tree with the use frequency of characters as the weight, and then use the Huffman tree to encode characters.
The core idea of Huffman coding is to make the leaf with large weight closest to the root.
Huffman tree algorithm steps
(you can look at the diagram directly)
Huffman tree is constructed by taking the character to be encoded as the leaf node, taking the frequency of the character in the file as the weight of the leaf node, and doing n-1 "merging" operations from bottom to top.
The greedy strategy adopted by Huffman algorithm is to take two trees without parents and with the smallest weight from the set of trees as the left and right subtrees each time, build a new tree, the weight of the root node of the new tree is the sum of the weight of its left and right child nodes, and insert the new tree into the combination of trees.
- Determine the appropriate data structure: the following situations should be considered before writing the program.
There is no node with degree 1 in Huffman tree, that is, a Huffman tree with N0 leaf nodes has 2n0 - 1 nodes.
After constructing Huffman tree, in order to find Huffman coding, we need to start from leaf node and have a path from leaf to root.
Decoding needs to start from the root and take a path from the root to the leaf. Then for each reception, you need to know the weight of each node, parents, left children, right children and node information.
-
Initialization: build a single node tree set with n nodes of n characters, T = {t1, t2,..., tn}. Each tree has only one weighted root node, and the weight is the frequency of use of the character.
-
If there is only one tree left in T, the Huffman tree is successfully constructed and skip to step 6. Otherwise, take out the two trees ti and tj with no parents and the smallest weight from the set t, and merge them into a new tree zk. The left child of the new tree is ti, the right child is tj, and the weight of zk is the sum of the weights of ti and tj.
-
Delete ti and tj from set T and add zk.
-
Repeat steps 3 and 4.
-
It is agreed that the code on the left branch is "0" and the code on the right branch is "1".
The Huffman code of each character is inversely obtained from the leaf node to the root node, then the string composed of characters on the path from the root node to the leaf node is the Huffman code of the leaf node, and the algorithm ends.
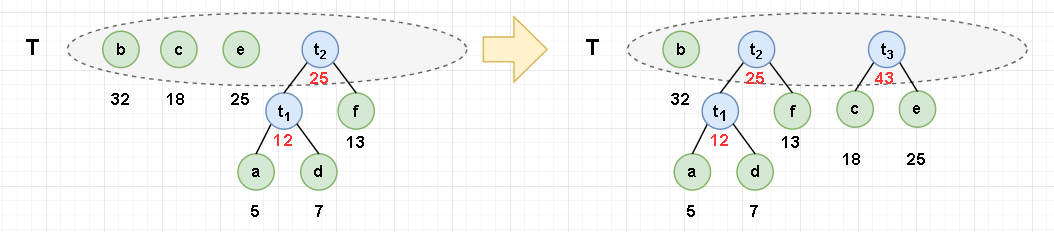
Huffman tree diagram
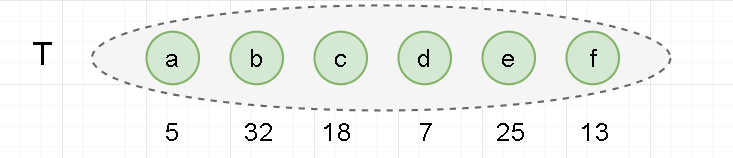
Construct a Huffman tree with the following characters and their frequencies to get their Huffman codes.

For the convenience of storage, we have expanded their frequency by 100 times.
a
:
5
,
b
:
32
,
c
:
18
,
d
:
7
,
e
:
25
,
f
:
13
a:5 ,b:32,c:18,d:7,e:25,f:13
a:5,b:32,c:18,d:7,e:25,f:13
- Initialization: build a single node tree set with n nodes and n characters. T = {a, b, c, d, e, f}.
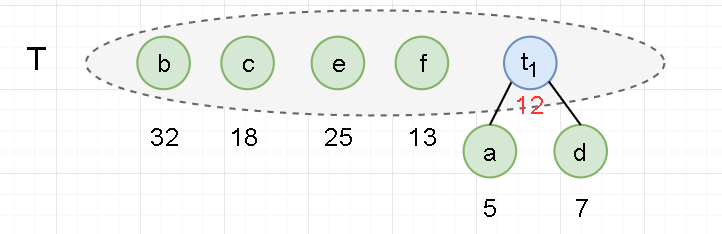
- Take out the two trees a and d without parents and with the smallest weight from the set t, and merge them into a new tree t1. The left child of the new tree is a, the right child is D, and the weight of the new tree is a+b = 12. The root t1 of the new tree is added to set t, and a and D are deleted from set t.
...
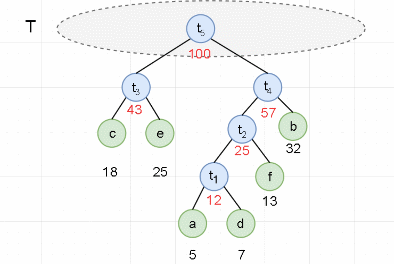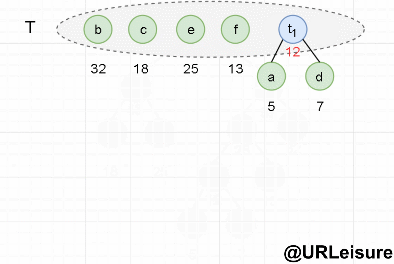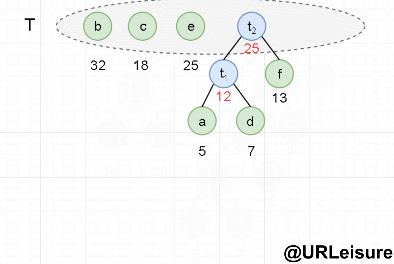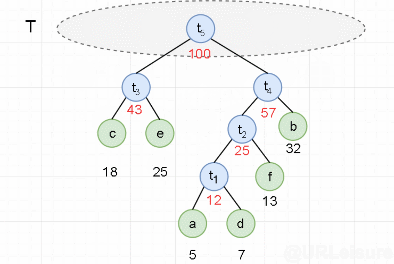
- It is agreed that the code on the left branch is "0" and the code on the right branch is "1".
The Huffman code of each character is inversely obtained from the leaf node to the root node. Then the string composed of characters on the path from the root node to the leaf node is the Huffman code of the leaf node.
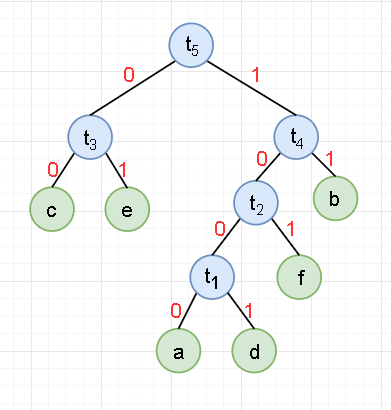
a
:
1000
,
b
:
11
,
c
:
00
,
d
:
1001
,
e
:
01
,
f
:
101
a:1000,b:11,c:00,d:1001,e:01,f:101
a:1000,b:11,c:00,d:1001,e:01,f:101
be careful:
In the figure below, there are two nodes with 25 weights. In order to reduce the number of layers of the tree, we give priority to the nodes with less layers.
Code implementation of Huffman tree
Our code is written in the most simple way, and the optimization code is at the end.
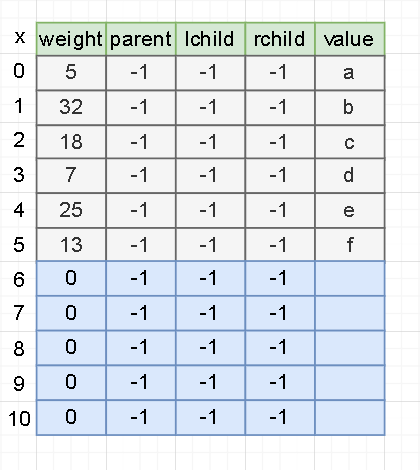
First declare the following: HuffNode [] stores all node information, and HuffCode [] stores Huffman codes of all nodes.
First create two structs (inner classes).
- Node structure: contains five fields: weight, parents, left child, right child and node character information.
- Huffman coding structure: contains coding array and record coding start subscript
The c + + code is as follows (example):
typedef struct HNode{
double weight;//Weight
int parent;//parents
int lchild;//Left child
int rchild;//Right child
char value;//Character information of current node
}*HNodeType;
typedef struct HCode{
int bit[MAXBIT];//Store positive coded array
int start;//Encoding start subscript
}HCodeType;
The java code is as follows (example):
public static class NodeType{
double weight;
int parent;
int lchild;
int rchild;
String value;
}
public static class CodeType{
int bit[] = new int[MAXBIT];
int start;
}
1). initialization
For example, our node information is as follows:
/* a 5 b 32 c 18 d 7 e 25 f 13 */
The c + + code is as follows (example):
void InitHuffmanTree(HNodeType HuffNode[],int n){
for(int i = 0;i<2*n-1;i++){//A total of 2n-1 nodes are deduced from the formula
HuffNode[i].weight = 0;
HuffNode[i].parent = -1;
HuffNode[i].lchild = -1;
HuffNode[i].rchild = -1;
}
for(int i = 0;i<n;i++){
cin>>HuffNode[i].value>>HuffNode[i].weight;
}
}
The java code is as follows (example):
public static NodeType[] initHuffmanTree(NodeType HuffNode[],int n){
for(int i = 0;i<2*n-1;i++){
HuffNode[i] = new NodeType();
HuffNode[i].weight = 0;
HuffNode[i].parent = -1;
HuffNode[i].lchild = -1;
HuffNode[i].rchild = -1;
}
for(int i = 0;i<n;i++){
HuffNode[i].value = sc.next();
HuffNode[i].weight = sc.nextDouble();
}
return HuffNode;
}
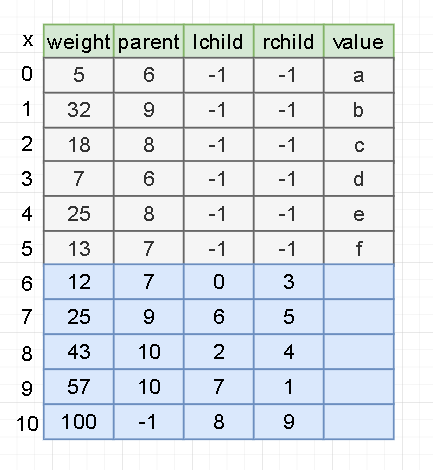
2). Circular tree building
Take out two trees ti and tj with parents of - 1 and the smallest weight from the set T, and merge them into a new tree zk. The left child is the node ti with the smallest weight, the right child is the next smallest node tj, and the weight of zk is the sum of the weights of ti and tj.
After completion, as shown in the figure:
Application of priority queue in algorithm optimization
The c + + code is as follows (example):
void HuffmanTree(HNodeType HuffNode[],int n){
int x1,x2;//x1. Minimum serial number x2 Sub minor serial number
double m1,m2;//m1. Minimum weight m2 Sub small weight
for(int i = 0;i<n-1;i++){//N nodes merged n-1 times
x1 = x2 = 0;
m1 = m2 = MAXVALUE;
for(int j = 0;j<n+i;j++){//Find out the two nodes without parents and with the minimum weight and merge them into a binary tree (the newly generated nodes also need to be arranged, so it is n+i)
double k = HuffNode[j].weight;
if(k<m1 && HuffNode[j].parent==-1){//Minor minimum replacement
x2 = x1;
m2 = m1;
x1 = j;
m1 = k;
}else if(k<m2 && HuffNode[j].parent==-1){//Minor replacement
x2 = j;
m2 = k;
}
}
HuffNode[n+i].weight = m1 + m2;//New node weight
HuffNode[n+i].lchild = x1;//New node left child minimum
HuffNode[n+i].rchild = x2;//New node right child Second small
HuffNode[x1].parent = n+i;//Additional parents
HuffNode[x2].parent = n+i;//Additional parents
}
}
The java code is as follows (example):
public static NodeType[] huffmanTree(NodeType HuffNode[],int n){
int x1,x2;
double m1,m2;
for(int i = 0;i<n-1;i++){
x1 = x2 = 0;
m1 = m2 = MAXVALUE;
for(int j = 0;j<n+i;j++){
double k = HuffNode[j].weight;
if(k < m1 && HuffNode[j].parent==-1){
m2 = m1;
x2 = x1;
x1 = j;
m1 = k;
}else if(k < m2 && HuffNode[j].parent == -1){
m2 = k;
x2 = j;
}
}
HuffNode[n+i].weight = m1+m2;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
}
return HuffNode;
}
3). Huffman coding
Our Huffman coding is to find the root from the leaf, while decoding needs to go from root to leaf, which is the opposite process.
So for convenience, we directly flashed the array.
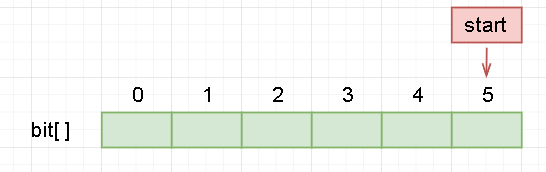
For example, we save a Huffman code of a:
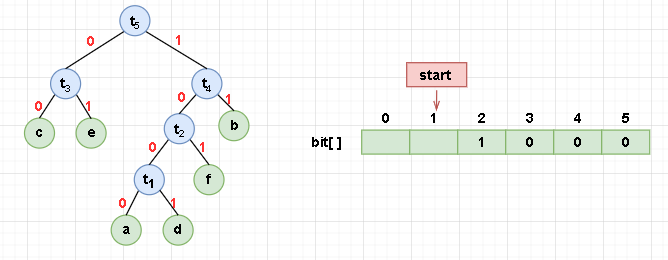
Our stored procedure is to first store 0 or 1 into the array, and then move start one bit to the left.
This causes start to be in front of the first available storage space, so finally we let start back one bit.
The c + + code is as follows (example):
void HuffmanCode(HCodeType HuffCode[],HNodeType HuffNode[],int n) {
HCodeType temp;
int p,cur;
for(int i = 0;i<n;i++){//N leaves, n stored
temp.start = n-1;// The array is stored from n-1
cur = i;//Current node serial number
p = HuffNode[cur].parent;//Currently connected to i but parents
while(p != -1){//Have parents
if(HuffNode[p].lchild == cur){//Determine whether cur is a left child
temp.bit[temp.start] = 0;
}else{//Determine whether it is a right child
temp.bit[temp.start] = 1;
}
temp.start --;//Shift left
cur = p;//Next node serial number
p = HuffNode[cur].parent;//Parents of the next node
}
HuffCode[i] = temp;//Copy the coded information
HuffCode[i].start += 1;//Shift right one bit
}
}
The java code is as follows (example):
public static CodeType[] huffmanCode(CodeType HuffCode[],NodeType HuffNode[],int n){
int cur,p;
for(int i = 0;i<n;i++){
HuffCode[i] = new CodeType();
HuffCode[i].start = n-1;
cur = i;
p = HuffNode[cur].parent;
while(p!=-1){
if(HuffNode[p].lchild == cur){
HuffCode[i].bit[HuffCode[i].start] = 0;
}else{
HuffCode[i].bit[HuffCode[i].start] = 1;
}
HuffCode[i].start --;
cur = p;
p = HuffNode[cur].parent;
}
HuffCode[i].start += 1;
}
return HuffCode;
}
4). Complete code
The c + + code is as follows (example):
#include<iostream>
#include<climits>
using namespace std;
#define MAXBIT 100 / / number of codes
#define MAXVALUE INT_MAX
#define MAXLEAF 30 / / number of leaves
#define MAXNODE (MAXLEAF*2-1) / / number of nodes
typedef struct HNode{
double weight;
int parent;
int lchild;
int rchild;
char value;
}HNodeType;
typedef struct HCode{
int bit[MAXBIT];
int start;
}HCodeType;
void InitHuffmanTree(HNodeType HuffNode[],int n){
for(int i = 0;i<2*n-1;i++){
HuffNode[i].weight = 0;
HuffNode[i].parent = -1;
HuffNode[i].lchild = -1;
HuffNode[i].rchild = -1;
}
for(int i = 0;i<n;i++){
cin>>HuffNode[i].value>>HuffNode[i].weight;
}
}
void HuffmanTree(HNodeType HuffNode[],int n){
int x1,x2;
double m1,m2;
for(int i = 0;i<n-1;i++){
x1 = x2 = 0;
m1 = m2 = MAXVALUE;
for(int j = 0;j<n+i;j++){
double k = HuffNode[j].weight;
if(k<m1 && HuffNode[j].parent==-1){
x2 = x1;
m2 = m1;
x1 = j;
m1 = k;
}else if(k<m2 && HuffNode[j].parent==-1){
x2 = j;
m2 = k;
}
}
HuffNode[n+i].weight = m1 + m2;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
}
}
void HuffmanCode(HCodeType HuffCode[],HNodeType HuffNode[],int n) {
HCodeType temp;
int p,cur;
for(int i = 0;i<n;i++){
temp.start = n-1;
cur = i;
p = HuffNode[cur].parent;
while(p != -1){
if(HuffNode[p].lchild == cur){
temp.bit[temp.start] = 0;
}else{
temp.bit[temp.start] = 1;
}
temp.start --;
cur = p;
p = HuffNode[cur].parent;
}
HuffCode[i] = temp;
HuffCode[i].start += 1;
}
}
int main(){
int n=6;
HNodeType HuffNode[MAXNODE];
InitHuffmanTree(HuffNode,n);
HuffmanTree(HuffNode,n);
HCodeType HuffCode[MAXLEAF];
HuffmanCode(HuffCode,HuffNode,n);
for(int i=0;i<n;i++){
cout<<HuffNode[i].value<<": Huffman code is:";
for(int j=HuffCode[i].start;j<n;j++){
cout<<HuffCode[i].bit[j];
}
cout<<endl;
}
return 0;
}
The java code is as follows (example):
import java.util.Scanner;
public class A {
private static int MAXBIT = 100;
private static int MAXVALUE = Integer.MAX_VALUE;
private static int MAXLEAF = 30;
private static int MAXNODE = MAXLEAF*2-1;
private static NodeType HuffNode[];
private static CodeType HuffCode[];
private static Scanner sc = new Scanner(System.in);
public static class NodeType{
double weight;
int parent;
int lchild;
int rchild;
String value;
}
public static class CodeType{
int bit[] = new int[MAXBIT];
int start;
}
public static NodeType[] initHuffmanTree(NodeType HuffNode[],int n){
for(int i = 0;i<2*n-1;i++){
HuffNode[i] = new NodeType();
HuffNode[i].weight = 0;
HuffNode[i].parent = -1;
HuffNode[i].lchild = -1;
HuffNode[i].rchild = -1;
}
for(int i = 0;i<n;i++){
HuffNode[i].value = sc.next();
HuffNode[i].weight = sc.nextDouble();
}
return HuffNode;
}
public static NodeType[] huffmanTree(NodeType HuffNode[],int n){
int x1,x2;
double m1,m2;
for(int i = 0;i<n-1;i++){
x1 = x2 = 0;
m1 = m2 = MAXVALUE;
for(int j = 0;j<n+i;j++){
double k = HuffNode[j].weight;
if(k < m1 && HuffNode[j].parent==-1){
m2 = m1;
x2 = x1;
x1 = j;
m1 = k;
}else if(k < m2 && HuffNode[j].parent == -1){
m2 = k;
x2 = j;
}
}
HuffNode[n+i].weight = m1+m2;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
}
return HuffNode;
}
public static CodeType[] huffmanCode(CodeType HuffCode[],NodeType HuffNode[],int n){
int cur,p;
for(int i = 0;i<n;i++){
HuffCode[i] = new CodeType();
HuffCode[i].start = n-1;
cur = i;
p = HuffNode[cur].parent;
while(p!=-1){
if(HuffNode[p].lchild == cur){
HuffCode[i].bit[HuffCode[i].start] = 0;
}else{
HuffCode[i].bit[HuffCode[i].start] = 1;
}
HuffCode[i].start --;
cur = p;
p = HuffNode[cur].parent;
}
HuffCode[i].start += 1;
}
return HuffCode;
}
public static void main(String[] args) {
int n=6;
NodeType huffNode[]=new NodeType[MAXNODE];
initHuffmanTree(huffNode,n);
huffmanTree(huffNode,n);
CodeType codeType[]=new CodeType[MAXLEAF];
huffmanCode(codeType,huffNode,n);
for(int i=0;i<n;i++){
System.out.print("Huffman code is"+huffNode[i].value+" ");
for(int j=codeType[i].start;j<n;j++){
System.out.print(codeType[i].bit[j]+" ");
}
System.out.println();
}
}
}
Algorithm complexity analysis of Huffman tree
- Time complexity
In HuffmanTree(), if (k < M1 & & huffnode [J]. Parent = = - 1) is the basic statement, and the outer layers i and j form a double-layer loop.
- When i = 0, the statement is executed n times;
- When i = 1, the statement is executed n+1 times;
- When i = 2, the statement is executed n+2 times;
- ...
- When i = n-2, the statement is executed n+n-2 times;
Therefore, the basic statements are executed:
n
+
(
n
+
1
)
+
(
n
+
2
)
+
.
.
.
+
(
n
+
n
−
2
)
=
(
n
−
1
)
(
3
n
−
2
)
2
n+(n+1)+(n+2)+ ... +(n+n-2) =\frac{(n-1)(3n-2)}{2}
n+(n+1)+(n+2)+...+(n+n−2)=2(n−1)(3n−2)
In the function HuffmanCode(), if the time complexity of encoding is close to n2, the time complexity of the algorithm is O ( n 2 ) O(n^2) O(n2).
- Spatial complexity
The required storage space is node structure array and coding structure array. There are 2n-1 nodes in Huffman tree array HuffmanNode [], of which n nodes contain bit [] and start fields, so the space complexity of the algorithm is O ( n × M A X B I T ) O(n × MAXBIT) O(n×MAXBIT).
Algorithm optimization of Huffman tree
- In the function HuffmanTree(), the priority queue is used when finding two nodes with the smallest weight, and the time complexity is O ( l o g n ) O(logn) O(logn), executed n-1 times, with a total time complexity of O ( n l o g n ) O(nlogn) O(nlogn).
When comparing, you should pay attention to two nodes with equal weight. At this time, you need to compare their serial number in HuffNode []. The higher the number, the fewer the layers. Therefore, when they are equal, the smaller the serial number will be ranked first.
The c + + code is as follows (example):
bool operator<(const HNodeType &a, const HNodeType &b) {
return a.weight > b.weight;//Ascending arrangement
}
void HuffmanTree1(HNodeType HuffNode[],int n){
HNodeType temp,x1,x2;//x1. Minimum term x2 Minor item
priority_queue<HNodeType> q;
for(int i = 0;i<n;i++){
q.push(HuffNode[i]);//Put in priority queue
}
int k = 0;
while(q.size()>1){//Equal to 1 means that all are merged, leaving the weight of 100
x1 = q.top();//minimum
q.pop();
x2 = q.top();//Second small
q.pop();
//Create a new node
temp.parent = -1;
temp.lchild = x1.index;
temp.rchild = x2.index;
temp.weight = x1.weight + x2.weight;
temp.index = n + k;//An index position variable is added to the node structure to determine the left and right child positions
HuffNode[x1.index].parent = n+k;//Add x1 parents
HuffNode[x2.index].parent = n+k;//Add x2 parents
HuffNode[n+k] = temp;//Add new node to node array
q.push(temp);//Add new node
k++;
}
}
The java code is as follows (example):
public static void huffmanTree1(NodeType HuffNode[],int n){
Queue<NodeType> queue = new PriorityQueue<>(new Comparator<NodeType>() {
@Override
public int compare(NodeType o1, NodeType o2) {
if(o1.weight > o2.weight ) {
return 1;
}else if(o1.weight == o2.weight && o1.index > o2.index){//In order to minimize the number of layers of the spanning tree, when the weight values are equal, we first select the one with the front serial number and the number of layers is less
return 1;
}
return -1;
}
});
for(int i = 0;i<n;i++){
queue.add(HuffNode[i]);
}
NodeType x1,x2,temp;
int k = 0;
while(queue.size() > 1){
x1 = queue.poll();
x2 = queue.poll();
temp = new NodeType();
temp.parent = -1;
temp.lchild = x1.index;
temp.rchild = x2.index;
temp.index = n + k;
temp.weight = x1.weight + x2.weight;
HuffNode[n+k] = temp;
HuffNode[x1.index].parent = n+k;
HuffNode[x2.index].parent = n+k;
queue.add(temp);
k++;
}
}
- In the function HuffmanCode(), Huffman coding array HuffNode [] can define a linear table with dynamically allocated space to store coding. The length of each linear table is the actual coding length, which can greatly save space.
This is too simple. Don't hit it. Just remember to reverse the position or output it in reverse order.
summary
The first time I got rid of Huffman tree, I was very stunned. I played more times and thought more, and I found it very simple.
Open the picture, open the picture! A lot of things!!!
Forecast for the next issue: basic theory of graph