strand

definition

A finite sequence of zero or more characters

The subsequence composed of any consecutive characters in the string is called the substring of the string

A string composed of one or more spaces is called a space string. A space string is not an empty string

There are also two storage structures for strings, sequential storage and chain storage, but considering the storage efficiency and the convenience of the algorithm, the string mostly adopts sequential storage structure

String storage is not difficult to implement, but string pattern matching is very important

Pattern matching algorithm

The location operation of substring is called string pattern matching or string matching. There are two strings, S and T. S is called the main string, also known as the text string, and T is called the substring, also known as the mode. Pattern matching is to find the substring matching the pattern T in the main string S. if successful, the position of the first character of the string in the main string is returned

1.BF algorithm

//Sequential storage of strings
//BF algorithm realizes string pattern matching
//Use the c + + library function string directly
#include<iostream>
#include<string>
using namespace std;

void Index_BF(string S,string T){//S main string, T sub string
    int i=0,j=0;
    while(i<=S.length()-1&&j<=T.length()-1){
        if(S[i]==T[j]){
            i++;
            j++;
        }else{
            i=i-j+1;//Once the search is wrong, i starts from the next bit, j starts from the first place, and the pointer traces back
            j=0;
        }
    }
    if(j>T.length()-1){//When exiting the loop, if j meets the condition, the match is reached, and if i meets the condition, the match fails
        cout<<"Match successful"<<endl;
        cout<<"The position of the substring in the main string is:"<<i-T.length()+1<<endl;
    }else{
        cout<<"Match failed"<<endl;
    }
}
int main(){
    string str="aaaabcd";
    string ttr="aabcd";
    Index_BF(str,ttr);
}

Worst case time complexity O(n*m): main string length N, substring length m, equivalent to two-layer for loop

2.KMP algorithm

Compared with the "BF" algorithm, the "KMP" algorithm has the following advantages:

• On the premise of ensuring that the pointer i does not backtrack, when the matching fails, move the pattern string to the right by the maximum distance;
• And the pattern matching operation of the string can be completed on the time order of O(n+m); Therefore, "KMP" algorithm is called "fast pattern matching algorithm".

On the premise of ensuring that the i pointer does not backtrack, if you want to realize the function, you can only let the j pointer backtrack

The backtracking distance of j pointer is equivalent to the distance that the mode string moves to the right. The longer the string j moves, the longer the pointer moves to the right.

For a given pattern string, each character may encounter matching failure. At this time, the corresponding j pointer needs to be backtracked. The specific backtracking position is actually determined by the pattern string itself, which has nothing to do with the main string

Calculate next array:

The calculation method is: for a character in the pattern string, extract the string in front of it, check the number of consecutive identical strings from both ends of the string, and then + 1 on the basis, and the result is the corresponding value of the character.

The value corresponding to the first character of each mode string is 0, and the value corresponding to the second character is 1.

For example: find the next of the pattern string "abcabac". The 0 and 1 corresponding to the first two characters are fixed.

For the character 'c', the extracted string 'ab', 'a' and 'b' are not equal. The number of the same string is 0, 0 + 1 = 1, so the next value corresponding to 'c' is 1;

The fourth character 'a', extract "abc", from the first 'a' and 'c' are not equal, the same number is 0, 0 + 1 = 1, so the next value corresponding to 'a' is 1;

The fifth character 'b', extract "abca", the first 'a' is the same as the last 'a', the same number is 1, 1 + 1 = 2, so the next value corresponding to 'b' is 2;

The sixth character 'a' extracts "abcab". The first two characters "ab" are the same as the last two "ab", and the same number is 2, 2 + 1 = 3, so the next value corresponding to 'a' is 3;

The last character 'c', extract "abcaba", the first character 'a' is the same as the last 'a', the same number is 1, 1 + 1 = 2, so the next value corresponding to 'c' is 2;

Therefore, the value in the next array corresponding to the string "abcabac" is (0,1,1,1,2,3,2).

The specific algorithm is as follows:

Mode string T is (subscript starts from 1): "abcabac" next array (subscript starts from 1): 01

The third character 'c': since the next value of the previous character 'b' is 1, take T[1] = 'a' and 'b' and compare them. They are not equal. Continue; End because next[1] = 0‘ c 'the corresponding next value is 1; (as long as next[1] = 0, the next value of this character is 1)

Mode string T is: "abcabac" next array (subscript starts from 1): 011

The fourth character 'a': since the next value of the previous character 'c' is 1, take T[1] = 'a' and 'c' and compare them. They are not equal. Continue; End because next[1] = 0‘ A 'the corresponding next value is 1;

Mode string T is: "abcabac" next array (subscript starts from 1): 0111

The fifth character 'b': since the next value of the previous character 'a' is 1, take T[1] = 'a' and 'a' to compare, equal and end‘ The next value corresponding to b 'is: 1 (the next value of the previous character' a ') + 1 = 2;

Mode string T is: "abcabac" next array (subscript starts from 1): 01112

The sixth character 'a': since the next value of the previous character 'b' is 2, T[2] = 'b' and 'b' are compared and equal, so it ends‘ The next value corresponding to a 'is: 2 (the next value of the previous character' b ') + 1 = 3;

Mode string T is: "abcabac" next array (subscript starts from 1): 011123

The seventh character 'c': since the next value of the previous character 'a' is 3, take T[3] = 'c' and 'a' and compare them. They are not equal. Continue; Since next[3] = 1, take T[1] = 'a' and 'a' to compare, equal and end‘ The next value corresponding to a 'is: 1 (the value of next [3]) + 1 = 2;

Mode string T is: "abcabac" next array (subscript starts from 1): 0111232

Implementation of KMP algorithm based on next

Let's take a look at the running process of KMP algorithm (assuming that the main string is ababcabbab and the mode string is abcac).

First match:

Second match:

Third match:

Principle understanding:

The i pointer keeps moving forward. When there is the same element in the substring, compare whether the element before it is the same as the element before the same element in the substring. If it is the same, continue to match the following elements. If it is different, check the next bit. Therefore, i does not need to backtrack and just move backward. j moves forward or backward to compare whether the elements are the same according to the situation

next stores the position of the same element sequence

realization

//Pattern matching of string
//KMP algorithm
#include<iostream>
#include<string>
using namespace std;

void getNext(string T,int next[]){//Find next array
    int i=1,j=0;
    next[1]=0;
    while(i<T.length()){
        if(j==0||T[i-1]==T[j-1]){//Subscript starts at 0
            i++;
            j++;
            next[i]=j;
        }else{
            j=next[j];
        }
    }
}
void Index_KMP(string S,string T,int next[]){
    int i=1,j=1;
    while(i<=S.length()&&j<=T.length()){
        if(j==0||S[i-1]==T[j-1]){
            i++;
            j++;
        }else{
            j=next[j];
        }
    }
    if(j>T.length()){
            cout<<"Match successful"<<endl;
            cout<<"T stay S The starting position in is:"<<i-T.length()<<endl;
        }else{
            cout<<"Match failed"<<endl;
        }
}

int main(){
    string str="aaaabcd";
    string ttr="aabc";
    int next[100];
    getNext(ttr,next);
    Index_KMP(str,ttr,next);
}

array

The array data structure can be directly realized by using the built-in array structure

Compressed storage of special matrix

Symmetric matrix:

It can be stored in a one-dimensional array

The realization process of symmetric matrix is that if the elements in the lower triangle are stored, only the row mark i and column Mark j of each element need to be substituted into the following formula: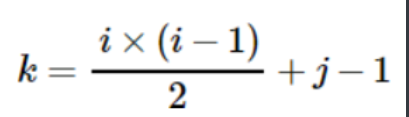

For the elements storing the upper triangle, the row mark i and column Mark j of each element shall be substituted into another formula:

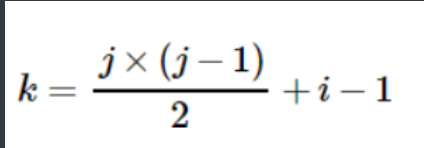
Upper and lower triangular matrix: it is also stored in one dimension

Sparse matrix:

A large number of zeros are distributed in the matrix

Save only non-zero elements

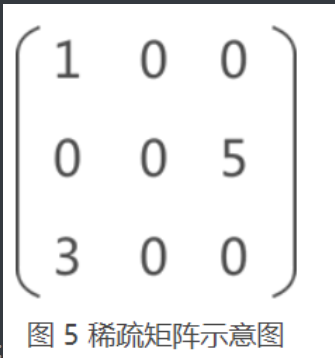
For example, to store the sparse matrix in Figure 5, the following information needs to be stored:

• (1,1,1): the data element is 1 and the position in the matrix is (1,1);
• (3,3,1): the data element is 3 and the position in the matrix is (3,1);
• (5,2,3): the data element is 5 and the position in the matrix is (2,3);
• In addition, the number of rows 3 and columns 3 of the matrix should be stored;

Ternary sequential table, triple representation of sparse matrix

Compress the sparse matrix into a triple array

//Triple storage sparse matrix
#include<iostream>
using namespace std;
#define number 20
class triple{
    public:
    int i,j;//Row mark i, column Mark j
    int data;//Element value
};

class TSMatrix{
    public:
    triple data[20];
    int n,m,num;//n: Number of rows; m: Number of columns; num: number of non-zero elements;
};

void initTsMatrix(TSMatrix &T){
    T.m=3;
    T.n=3;
    T.num=3;//Sparse matrix with three rows, three columns and three non-zero elements

    T.data[0].i=1;
    T.data[0].j=1;
    T.data[0].data=1;

    T.data[1].i=2;
    T.data[1].j=3;
    T.data[1].data=5;

    T.data[2].i=3;
    T.data[2].j=1;
    T.data[2].data=3;
}

void display(TSMatrix T){
    for(int i=1;i<=T.n;i++){//The position of non-zero elements starts with 1
        for(int j=1;j<=T.m;j++){
            int value=0;
            for(int k=0;k<T.num;k++){
                if(i==T.data[k].i && j==T.data[k].j){
                    cout<<T.data[k].data<<" ";
                    value=1;
                    break;
                }  
            }
            if(value==0){
                cout<<"0"<<" ";
            }


        }
        cout<<endl;
    }
}

int main(){
    TSMatrix T;
    initTsMatrix(T);
    display(T);
}

 

Generalized table

definition

Generalized tables, also known as lists, can store both non separable elements and generalized tables

Generally, a single element in a generalized table is called "atom", and the stored generalized table is called "sub table"

Similar to the set in Mathematics

Header and footer

When the generalized table is not empty, the first data is called the header, which can be a single element or sub table. The new generalized table composed of the remaining data is the footer

eg: in the generalized table, LS={1,{1,2,3},5}, the header is atom 1, and the tail is the generalized table composed of sub table {1,2,3} and atom 5, that is {1,2,3}, 5}.

For another example, in the generalized table LS = {1}, the header is atom 1, but since there is no footer element in the generalized table, the footer of the table is an empty table, represented by {}.

realization

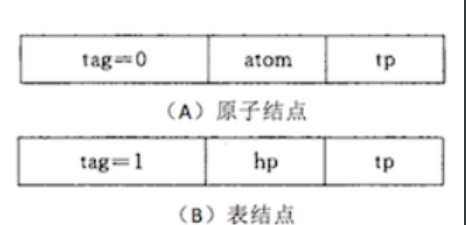
The node representing the atom is composed of tag bit, atomic value and tp pointer, and the node representing the sub table is also composed of tag bit, hp pointer and tp pointer.

 

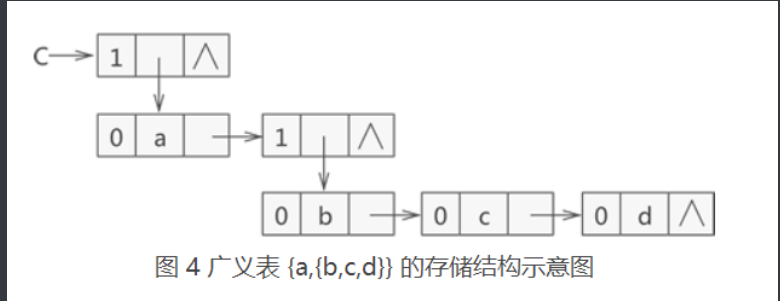
//Generalized table
//Storage tables {a,{b,c,d}};
#include <iostream>
using namespace std;

class glist{
public:
    int tag;   //Flag field
    char atom; //Atomic node range
    glist *hp; //Point to header
    glist *tp; //Point to the next element
};

typedef glist *Glist;

void createList(Glist &L){
    //Node 1
    L = (Glist)malloc(sizeof(glist));
    L->tag = 1;
    L->hp = (Glist)malloc(sizeof(glist));
    L->tp = NULL;
    //Node 2
    L->hp->tag = 0;
    L->hp->atom = 'a';
    L->hp->tp = (Glist)malloc(sizeof(glist));
    //Node 3
    L->hp->tp->tag = 1;
    L->hp->tp->hp = (Glist)malloc(sizeof(glist));
    L->hp->tp->tp = NULL;
    //Node 4
    L->hp->tp->hp->tag = 0;
    L->hp->tp->hp->atom = 'b';
    L->hp->tp->hp->tp = (Glist)malloc(sizeof(glist));
    //Node 5
    L->hp->tp->hp->tp->tag = 0;
    L->hp->tp->hp->tp->atom = 'c';
    L->hp->tp->hp->tp->tp = (Glist)malloc(sizeof(glist));
    //Node 6
    L->hp->tp->hp->tp->tp->tag = 0;
    L->hp->tp->hp->tp->tp->atom = 'd';
    L->hp->tp->hp->tp->tp->tp = (Glist)malloc(sizeof(glist));
    //End flag
    L->hp->tp->hp->tp->tp->tp->tag=-1;
}
// tap==1, then the lower level of L has a value, l = L - > HP
// Tap = = 0, the same level of L has a value, l = L - > TP
//The exit condition is tag = = 0 & & L - > TP = = null (non empty table)
void display(Glist L){
    while(1){
        if (L->tag==1){
            L = L->hp;
            cout<<"{";
        }else if(L->tag==0){
            cout << L->atom;
            L = L->tp;
        }else{
            break;
        }
    }
    cout<<"}";

}

int main(){
    Glist L;
    createList(L);
    display(L);

}