Question 1: ASCII code
[problem description]
It is known that the ASCII code of capital letter A is 65. What is the ASCII code of capital letter L?
[answer submission]
This is a question filled in with results. You just need to calculate the results and submit them. The result of this question is one
An integer. Only fill in this integer when submitting the answer. If you fill in the extra content, you will not be able to score.
Answer: simple, no explanation
76
Question 2: card – cycle of violence
Xiaolan has many digital cards, each with numbers 0 to 9.
Xiaolan is going to use these cards to spell some numbers. He wants to spell positive integers from 1. Each time he spell one, he will save it. The card can't be used to spell other numbers.
Xiaolan wants to know how much she can spell from 1.
For example, when Xiaolan has 30 cards, including 3 cards from 0 to 9, Xiaolan can spell 1 to 10, but when spell 11, there is only one card 1, which is not enough to spell 11.
Now Xiaolan has 2021 cards from 0 to 9, a total of 20210. How many can Xiaolan spell from 1?
Tip: it is recommended to use computer programming to solve the problem.
Idea:
Cycle of violence, pay attention to the conditions for the end of the cycle
answer:
3181
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
//Number of occurrences of 0-9
int index[] = new int[9];
flag:for (int i = 1; ; i++) {
int[] ints = new int[String.valueOf(i).length()];
//Convert int to int array
for (int j = 0; j < String.valueOf(i).length(); j++) {
//Get each number of the array
ints[j] = Integer.parseInt(String.valueOf(String.valueOf(i).charAt(j)));
//Traverse add number
for (int k = 0; k < 9; k++) {
if(ints[j]==k){
index[k]++;
//Note the end condition. When it is equal to 2021, it means that all cards are used up, and i is output at this time
if (index[k]==2021){
System.out.println(i);
System.out.println("Number of cards used at this time"+Arrays.toString(index));
break flag;
}
continue;
}
}
}
}
}
}
Question 3: straight line – Set / floating point operation
In the plane rectangular coordinate system, two points can determine a straight line. If there are multiple points on a straight line, the straight line determined by any two of these points is the same.
2 on a given plane × Three integer points {(x, y)|0 ≤ x < 2, 0 ≤ y < 3, X ∈ Z, y ∈ Z}, i.e. points where the abscissa is an integer between 0 and 1 (including 0 and 1) and the ordinate is an integer between 0 and 2 (including 0 and 2). These points determine a total of 11 different lines.
20 on a given plane × 21 integer points {(x, y)|0 ≤ x < 20, 0 ≤ y < 21, X ∈ Z, y ∈ Z}, that is, points where the abscissa is an integer between 0 and 19 (including 0 and 19) and the ordinate is an integer between 0 and 20 (including 0 and 20). How many different straight lines are determined by these points
Idea:
Straight line y = kx + b = = "k and b are the same, which is a straight line
Violence cycle, and use set set to remove duplication
How to find the second point of the quadruple cycle is the key, which needs to be considered
Note that the slope does not exist
answer:
40257
import java.util.HashSet;
public class Main {
public static void main(String[] args) {
HashSet<String> set=new HashSet<>();//There cannot be the same element in a set of dissimilarity with set
double k,b;
for(int x1=0;x1<20;x1++){
for(int y1=0;y1<21;y1++){
for(int x2=x1+1;x2<20;x2++){
for(int y2=0;y2<21;y2++){
k=(y2-y1)*1.0/(x2-x1);
b=(y1*x2-x1*y2)*1.0/(x2-x1);//Be careful to multiply by 1.0 with a decimal slope
set.add(k+","+b);//Each point is represented by a string
}
}
}
}
for (String s :
set) {
System.out.println(s);
}
System.out.println(set.size()+20);//Finally, remember to add that the slope does not exist
}
}
Question 4: cargo placement - factor of large number
Title details:
Xiaolan has a large warehouse, which can put a lot of goods.
Now, Xiaolan has n boxes of goods to be placed in the warehouse, and each box of goods is a regular cube. Xiaolan stipulates three mutually perpendicular directions of length, width and height. The side of each box of goods must be strictly parallel to the length, width and height.
Xiaolan hopes that all the goods will eventually be placed into a big cube. That is, pile L, W and H goods respectively in the direction of length, width and height, and meet the requirement of n = L × W × H.
Given n, how many schemes for stacking goods meet the requirements.
For example, when n = 4, there are six schemes: 1 × one × 4,1 × two × 2,1 × four × 1,2 × one × 2,2 × two × 1,4 × one × 1.
How many schemes are there when n = 2021041820210418 (note that there are 16 digits)?
Tip: it is recommended to use computer programming to solve the problem.
Idea:
If you solve it with java violence... You don't have to run in four hours
Main code of violence resolution attached
for (x = BigDecimal.ONE; x.compareTo(num) <= 0; x=x.add(BigDecimal.ONE)) {
for (y = BigDecimal.ONE; y.compareTo(num) <= 0; y=y.add(BigDecimal.ONE)) {
for (z = BigDecimal.ONE; z.compareTo(num) <= 0; z=z.add(BigDecimal.ONE)) {
if ((x.multiply(y).multiply(z)).compareTo(num) == 0) {
System.out.println(x+" y="+y);
ans++;
}}}}
System.out.println(ans);
Therefore, it needs to be improved. Considering that all the factors of the input number can be obtained first, and then these factors can be used to establish a three-layer cycle, and the results can be obtained quickly (because even in the three-layer cycle structure, the cycle times of each layer are greatly reduced and the speed is considerable). At this time, there is a problem about how to calculate the factor. I share an experience gained when brushing Leetcode, that is, traversing from 1 to the square order of magnitude of the digit. For each digit, use the ordinary method to judge whether it is a factor (whether to divide by whole). If divided by whole, the currently traversed value is a factor, and judge whether the value of the input digit divided by the current digit is equal to the current number, If not, the quotient is also a factor, which greatly reduces the order of magnitude of the common factor. The Java code implementation of the algorithm is as follows
answer:
2430
import java.util.*;
public class Main{
public static void main(String[] args) {
long n = 2021041820210418l;
int count = 0;
List<Long> list = new ArrayList<>();
for (long i = 1; i * i <= n; i++) {
//The method of finding all common factors greatly improves the efficiency
if (n % i == 0) {
list.add(i);
if (i != n / i) {
list.add(n / i);
}
}
}
for (long i : list) {
for (long j : list) {
for (long k : list) {
if (i * j * k == n) {
count++;
break;
}
}
}
}
System.out.println(count);
}
}
Question 5: path – dijkstra algorithm
Xiaolan is very happy after learning the shortest path. He defines a special graph and hopes to find the shortest path in the graph.
The diagram of Xiaolan consists of 2021 nodes, numbered from 1 to 2021.
For two different nodes a and b, if the absolute value of the difference between a and b is greater than 21, there is no edge connection between the two nodes; If the absolute value of the difference between a and b is less than or equal to 21, there is an undirected edge with a length of the least common multiple of a and b.
For example, there is no edge connection between node 1 and node 23; There is an undirected edge between node 3 and node 24, with a length of 24; There is an undirected edge between node 15 and node 25, with a length of 75.
Please calculate the shortest path len gt h between node 1 and node 2021. – > (obviously using Dijkstra algorithm)
Tip: it is recommended to use computer programming to solve the problem.
Idea:
First find the maximum common divisor, and then find the minimum common multiple (the idea is below). In this way, you can get an undirected graph 2021 * 2021, store the graph with the adjacency matrix, and then find the shortest path by dijkstra algorithm
dijkstra algorithm summary: breadth first traversal, find the shortest path to a point each time, and there are detailed comments in the code
Euclidean algorithm, also known as rolling division, is used to calculate the greatest common divisor GCD (greater common divisor) of two integers a and B. Its calculation principle depends on the following theorem:
Theorem: GCD (a, b) = GCD (B, a, mod, b)
int Gcd(int a, int b)
{
if(b == 0)
return a;
return Gcd(b, a % b);
}
Then use the greatest common divisor to find the least common multiple
The product of two numbers is equal to the product of the greatest common divisor and the least common multiple of the two numbers. Suppose two numbers are a and b, their greatest common divisor is p and their least common multiple is q. Then there is such a relationship: ab=pq
answer:
10266837
public class Main {
//Answer: 10266837
final static int C = 999999999;//Define that there is no direct at this point
public static void main(String[] args) {
//Initialize adjacency matrix
int[][] map = new int[2050][2050];
//First initialize to the maximum value
for (int[] temp : map) {
for (int i = 0; i < temp.length; i++) {
temp[i] = C;
}
}
//Assign value according to the meaning of the question
for (int i = 1; i <= 2021; i++) {
for (int j = i; j <= i + 21; j++) {
//Weight the edge with the difference between a and B within 21
map[i][j] = lcm(i, j);
}
}
//Dijkstra: generate the shortest path in the order of increasing path length
/*
V:Represents all vertices
bj:Represents whether the vertex has determined the shortest path
*/
boolean bj[] = new boolean[2050];//Used to mark whether the point has found the shortest path
int dis[] = new int[2050];//Stores the initial path from the source point to other vertices
for (int i = 1; i <= 2021; i++)
dis[i] = map[1][i];//Assign value to direct path first
int min, minIdx = 0;
//The while loop is not executed once to determine the shortest path to a point
while (!bj[2021]) {//If the shortest path at 2021 has not been found, it will continue to cycle
min = Integer.MAX_VALUE;
//Find the nearest distance from the source every time
for (int i = 2; i <= 2021; i++) {
if (!bj[i] && dis[i] < min) {
//exchange
min = dis[i];
minIdx = i;
}
}
bj[minIdx] = true;//After one cycle, the shortest point can be determined, and then the next cycle can be carried out until bj[2021]==true
//From the nearest point as the middle point, find v (0) -- V(minIdx) -- V (the point directly connected with V(minIdx)) and update the shortest path again
for (int i = minIdx + 1; i <= minIdx + 21; i++) {
//If there is no edge from this point to the source point
if (dis[i] == C)
dis[i] = dis[minIdx] + map[minIdx][i];
//The sum of both sides is less than the direct edge, and the distance is updated
else if (dis[minIdx] + map[minIdx][i] < dis[i])
dis[i] = dis[minIdx] + map[minIdx][i];
}
}
System.out.println(dis[2021]);
}
//greatest common factor
public static int gcd(int x, int y) {
if (y == 0)
return x;
return gcd(y, x % y);
}
public static int lcm(int x, int y) {//Least common multiple
return x * y / gcd(x, y);
}
}
Question 6: time display - Calendar
Xiaolan wants to cooperate with her friends to develop a time display website. On the server, the friend has obtained the current time, which is expressed as an integer. The value is the number of milliseconds from 00:00:00 on January 1, 1970 to the current time.
Now, Xiaolan will display this time on the client. Xiaolan doesn't need to display the year, month and day. It only needs to display the hours, minutes and seconds, and milliseconds. It can be directly rounded off.
Given a time expressed as an integer, please output the hour, minute and second corresponding to this time.
[input format]
The input line contains an integer representing the time.
[output format]
Output the current time represented by hour, minute and second. The format is HH:MM:SS, where HH represents hour, minute and second
From 0 to 23, MM represents minutes, values from 0 to 59, SS represents seconds, and values from 0 to 59. Hour, minute and second
If it is less than two digits, make up the leading 0.
[example input 1]
46800999
[sample output 1]
13:00:00
[example input 2]
1618708103123
[sample output 2]
01:08:23
[evaluation case scale and agreement]
For all evaluation cases, the given time is a positive integer no more than 10 ^ 18
Idea:
Just use the java date class to add a large number many times
However, there is a pit in the problem, which can be ignored in less than 1ms, so it needs to be dealt with
1. Calender class deals with time less than 1s
2. Api call of Calendar class for date format conversion
import java.math.BigDecimal;
import java.text.SimpleDateFormat;
import java.util.*;
public class Main {
public static void main(String[] args) {
Calendar date = Calendar.getInstance();
//Initialize date object
date.set(1970,1,1,0,0,0);
Scanner scanner = new Scanner(System.in);
BigDecimal num = scanner.nextBigDecimal();
BigDecimal temp = new BigDecimal("20000000");
BigDecimal[] arr = num.divideAndRemainder(temp);
for (int i = 0; i < arr[0].intValue(); i++) {
date.add(Calendar.MILLISECOND,20000000);
}
date.add(Calendar.MILLISECOND,arr[1].intValue()/1000*1000);
SimpleDateFormat format = new SimpleDateFormat("HH:mm:ss");
System.out.println(date.getTime());
String ans = format.format(date.getTime());
System.out.println(ans);
}
}
Question 7: minimum weight
You have a balance. Now you need to design a set of weights, so that you can use these weights to weigh any positive integer weight less than or equal to N.
How many weights should this set of weights contain at least?
Note that the weight can be placed on both sides of the balance.
[input format]
Enter an integer N.
[output format]
Output an integer representing the answer.
[sample input]
7
[sample output]
3
[example description]
The weights of the three weights are 1, 4 and 6, which can weigh all the weights from 1 to 7.
1 = 1;
2 = 6 - 4 (put 6 on one side and 4 on the other side of the balance);
3 = 4 - 1;
4 = 4;
5 = 6 - 1;
6 = 6;
7 = 1 + 6;
It is impossible to weigh all weights from 1 to 7 with less than 3 weights.
[evaluation case scale and agreement]
For all evaluation cases, 1 ≤ N ≤ 1000000000.
Idea: I don't quite understand this problem. It seems to involve balanced ternary system
Law: when there are x weights, you can weigh up to any positive integer weight less than or equal to 3 ^ 0 + 3 ^ 1 + 3 ^ 2 + ···· + 3 ^ (x-1)
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long n = sc.nextLong();
long ans = 0;
while(n>0) {
n -= Math.pow(3, ans);
ans++;
}
System.out.println(ans);
}
}
Question 8: Yang Hui triangle - don't understand
The following figure is the famous Yang Hui triangle:
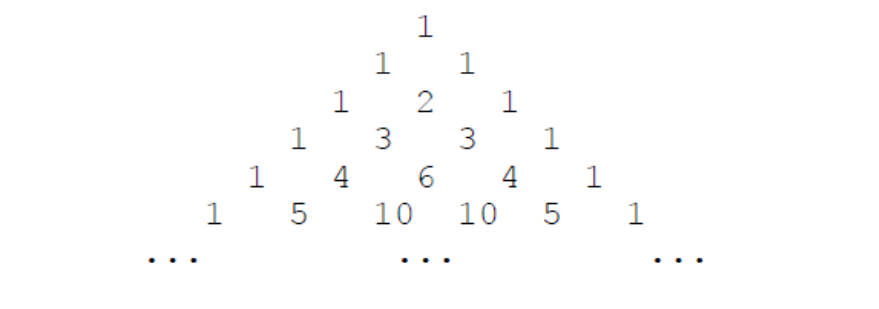
If we arrange all numbers in a row from top to bottom and from left to right, we can get the following sequence:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...
Given a positive integer n, what number is the first occurrence of N in the output sequence?
[input format]
Enter an integer N.
[output format]
Output an integer representing the answer.
[sample input]
6
[sample output]
13
[evaluation case scale and agreement]
For 20% of the evaluation cases, 1 ≤ N ≤ 10;
For all evaluation cases, 1 ≤ N ≤ 1000000000.
Idea:
Generate Yang Hui triangle directly and judge the first occurrence times. It is found that the data is too large, resulting in an exception Lang. outofmemoryerror: Java heap space, so this method is not advisable
Attached code: score 40
public static void main(String[] args) {
int ans = 1;
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
long[][] longs = new long[1001200][10000];
//Generate Yang Hui triangle and judge the number of occurrences for the first time
for (int i = 0; i < 50000; i++) {
for (int j = 0; j < i; j++) {//Traverse each number
if (i == j || j == 0) {
longs[i][j] = 1;
} else {
longs[i][j] = longs[i - 1][j - 1] + longs[i - 1][j];
}
if (longs[i][j] == num) {
System.out.println(ans);
return;
} else ans++;
}
}
}
Therefore, we need to change a way of thinking: the relationship between Yang Hui triangle and combinatorial number
With the idea of DP:
C (n, m) = how many ways to select m items from n items
The dynamic equation of Yang Hui is exactly the dynamic equation of the triangle
f[i ] [j ] = f [i−1] [j−1] + f[i−1] [ j ]
Correct code
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(sc.hasNext()) {
System.out.println(solve(sc.nextLong()));
}
}
public static long solve(long n) {
long res = 0l;
long san[] = new long[50010];
san[1]=1;
//san[x] indicates the x-th position of the current layer. This is to facilitate the implementation of san[j] = san[j-1]+san[j] at the first position of each layer, so that the array does not cross the boundary
if(n==1)return 1;
long cur=0l;
for(int i=2;i<50000;i++) {
//cur is now in the last position in the upper layer
//Then pass + i to the first position of this floor, and then add i-1 to the last position of this floor
//Together, cur+2*i-2
cur+=2*i-1;
for(int j=i;j>=1;j--) {
san[j] = san[j-1]+san[j];
if(san[j]==n)res=cur;
cur--;
}
//There is still --, after it is reduced to the first position of this layer, so the position of cur after the circulation of one layer will reach the last position of the upper layer
//The next cycle is i + +, so the position of cur before the start of the next cycle is the last position of the upper layer
if(res!=0)return res;
}
//The number n cannot be found in the first 50000 lines, that is, the number n cannot appear in the second position after 50000 lines
//Because the value of the second position after 50000 lines is greater than 1000000000, the first position of N must be the third position of line n+1, that is, the value of C superscript 1 and subscript n
return (n+1)*n/2+2;
//The first row is a number, the nth row is n numbers, and it is an arithmetic sequence. Use the arithmetic sequence summation formula to calculate the value of the first n rows plus 2 is the position of the second number in n+1 row
}
}
Question 9: two way ranking - violent Api
Given sequence (a1, a2, ····, an) = (1, 2, ···, n), i.e. ai = i.
Xiaolan will perform m operations on this sequence. Each time, it may arrange a1, a2, ···, aqi in descending order or aqi, aqi+1, ···, an in ascending order.
Request the sequence after the operation is completed.
[input format]
The first line of input contains two integers n and m, which respectively represent the length of the sequence and the number of operations. Next, line m describes the operation on the sequence, where line i contains two integers pi
, qi indicates the operation type and parameters. When pi = 0, it means that a1, a2, ····, aqi are arranged in descending order; When pi = 1, indicates
Arrange aqi, aqi+1, ···, an in ascending order.
[output format]
Output a line containing n integers, separated by a space between adjacent integers, indicating the operation
Sequence after completion.
[sample input]
3 3
0 3
1 2
0 2
[sample output]
3 1 2
[example description]
The original sequence is (1, 2, 3).
After step 1 is (3, 2, 1).
After step 2 is (3, 1, 2).
After step 3 is (3, 1, 2). The same as after step 2, because the first two numbers are in descending order.
[evaluation case scale and agreement]
For 30% of the evaluation cases, n, m ≤ 1000;
For 60% of the evaluation cases, n, m ≤ 5000;
For all evaluation cases, 1 ≤ n, m ≤ 100000, 0 ≤ ai ≤ 1, 1 ≤ bi ≤ n.
Idea:
First of all, this solution only has 60 points (it's good in the game). Other test examples will timeout, but this is the easiest way to understand
You need full marks to see the solution to this problem
https://www.acwing.com/video/2845/
Arrays.sort(), pay attention to arrays How to reverse sort
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int length = sc.nextInt();//Array length
int op = sc.nextInt();//Number of operations
//Initialize array
Integer[] arr = new Integer[length];
for (int i = 0; i < length; i++) arr[i] = i + 1;
for (int i = 0; i < op; i++) {
//Accept two numbers and process
int num = sc.nextInt();
int num2 = sc.nextInt();
if (num == 0) {// AI an descending order
//Descending order
//Element sorting from fromIndex to toIndex-1!!!
Arrays.sort(arr, 0, num2, new Comparator<Integer>() {
public int compare(Integer a, Integer b) {
return b - a;
}
});
continue;
}
if (num == 1) {
Arrays.sort(arr, num2-1, length);
continue;
}
}
for (int i : arr) System.out.print(i + " ");
}
}
Question 10: parenthesis sequence
Given a bracket sequence, it is required to add as few brackets as possible to make the bracket sequence legal. When the addition is completed, different addition results will be produced. How many essentially different addition results are there. The two results are essentially different, which means that there is a certain position. One result is a left parenthesis and the other is a right parenthesis
number.
For example, for the bracket sequence ((()), you only need to add two brackets to make it legal. There are several different adding results: () () (), () () () (), () (), and (()).
[input format]
The input line contains a string s, which represents the given sequence of parentheses. There are only left parentheses and left parentheses in the sequence
Right parenthesis.
[output format]
Output an integer to represent the answer. The answer may be large. Please output the answer divided by 1000000007 (i.e
The remainder of 10 ^ 9 + 7).
[sample input]
((()
[sample output]
5
[evaluation case scale and agreement]
For 40% of the evaluation cases, | s | ≤ 200.
For all evaluation cases, 1 ≤| s | ≤ 5000