1: Foreword
friends who have studied Java must have used the four Java collection tools: Comparable, Comparator, Collections and Arrays. I just want to ask you, do these four tools smell good? Very fragrant, ha ha ha. In my opinion, the better the interface tools are used, the less simple the underlying principle implementation will be. Therefore, in this article, let's go deep into these four tools and explore the context of their implementation.
this article is too long. Readers are advised to read it selectively according to their own situation and the catalogue.
2: The collection framework is connected with Collections, Arrays, Comparable and Comparator
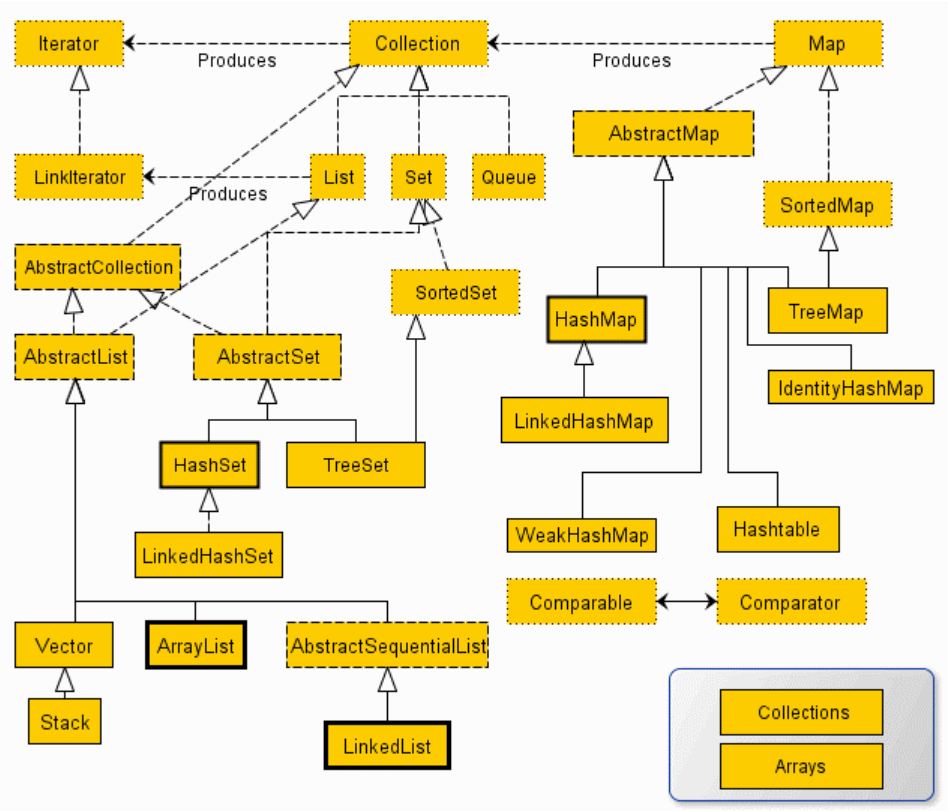
although the collective framework is not our theme today, it is closely related to our four protagonists today. Comparable, Comparator, Arrays and Collections are collection tools provided by Java. As long as we write according to the requirements of the rules, we can easily achieve the purpose we want to achieve. Next, let's talk about the two interfaces of comparable and Comparator.
3: Comparable interface and Comparator interface
Comparable is a sort interface (java.lang), and Comparator (java.util) is a Comparator interface. They both do the same thing: sorting. Let's first understand them through their UML diagrams.
2.1 UML diagram of comparable interface and Comparator interface
the structure of Comparable is relatively simple. There is an abstract method compareTo(T):

Compared with the Comparable interface, the Comparator interface provides two abstract methods: compare(T,T), equals(Obj), and multiple concrete methods.
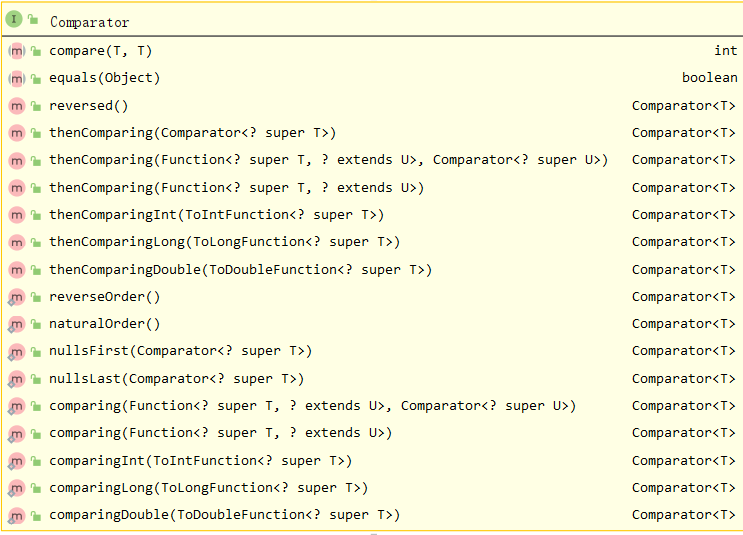
Now let's analyze the source code of the two through a program:
Let me tell you first that the return value of rewriting the comparison method is int, - 1 means that the former is less than the latter and in ascending order, 1 means that the former is greater than the latter and in descending order, and 0 means equal, then the next group of comparison is carried out
2.2.1 explore the underlying comparison principle of Comparable through a program
public class Test1 {
public static void main(String[] args) throws Exception {
SortByComparable test1 = new SortByComparable("acb",12);
SortByComparable test2 = new SortByComparable("ab",24);
SortByComparable test3 = new SortByComparable("acb",6);
SortByComparable[] arr = new SortByComparable[3];
arr[0]=test1;
arr[1]=test2;
arr[2]=test3;
Arrays.sort(arr);
for(SortByComparable t: arr){
System.out.println(t);
}
}
}
class SortByComparable implements Comparable<SortByComparable>{
String name;
int age;
public SortByComparable(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public int compareTo(SortByComparable another) {
if(!another.name.equals(this.name)){//String comparison: compare the ASCII values corresponding to each character from left to right. If they are the same, go to the next and return
return this.name.compareTo(another.name);//Single ASCII character in ascending order, corresponding to - 1 in ascending order, who in ascending order, who in ascending order
}else{//The same name is better than the second item
return this.age-another.age;//The younger ones rank first, which is equivalent to returning - 1 in ascending order
}
}
@Override
public String toString() {
return "i am " +
name + '\'' +
", my age is" + age ;
}
}
The operation results are as follows:
Arrays Relevant source code of tool class:
public class Arrays {
//LegacyMergeSort is a static inner class of Arrays
//Why do you have this static inner class?
//The jdk annotation says this:
/*
The old merge sort can be selected (compatible with the damaged comparator) to use the system properties,
Cannot be a static Boolean in a closed class due to a dependency loop.
The inner class will be deleted in future versions.
*/
//Summary: address compatibility
static final class LegacyMergeSort {
private static final boolean userRequested =
java.security.AccessController.doPrivileged(
new sun.security.action.GetBooleanAction(
"java.util.Arrays.useLegacyMergeSort")).booleanValue();
}
/
public static void sort(Object[] a) {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a);
else
ComparableTimSort.sort(a, 0, a.length, null, 0, 0);
}
//
static void sort(Object[] a, int lo, int hi, Object[] work, int workBase, int workLen) {
assert a != null && lo >= 0 && lo <= hi && hi <= a.length;
int nRemaining = hi - lo;
if (nRemaining < 2)
return; // Arrays of size 0 and 1 are always sorted
// If array is small, do a "mini-TimSort" with no merges
if (nRemaining < MIN_MERGE) {//Here, MIN_MERGE defaults to 32
int initRunLen = countRunAndMakeAscending(a, lo, hi);
binarySort(a, lo, hi, lo + initRunLen);//Perform binary search
return;
}
/**
* March over the array once, left to right, finding natural runs,
* extending short natural runs to minRun elements, and merging runs
* to maintain stack invariant.
*/
ComparableTimSort ts = new ComparableTimSort(a, work, workBase, workLen);
int minRun = minRunLength(nRemaining);
do {
// Identify next run
int runLen = countRunAndMakeAscending(a, lo, hi);
// If run is short, extend to min(minRun, nRemaining)
if (runLen < minRun) {
int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen);
runLen = force;
}
// Push run onto pending-run stack, and maybe merge
ts.pushRun(lo, runLen);
ts.mergeCollapse();
// Advance to find next run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
// Merge all remaining runs to complete sort
assert lo == hi;
ts.mergeForceCollapse();
assert ts.stackSize == 1;
}
/
//Returns the array operation length of the specified range. If there is descending order in the process, reverse the range to ensure that it is in ascending order
private static int countRunAndMakeAscending(Object[] a, int lo, int hi) {
assert lo < hi;
int runHi = lo + 1;
if (runHi == hi)
return 1;
// Find end of run, and reverse range if descending
//Find. If there are descending, invert the array of the range
if (((Comparable) a[runHi++]).compareTo(a[lo]) < 0) { // Descending, enter our specified rules for comparison
while (runHi < hi && ((Comparable) a[runHi]).compareTo(a[runHi - 1]) < 0)
runHi++;
reverseRange(a, lo, runHi);//Array inversion
} else { // Ascending
while (runHi < hi && ((Comparable) a[runHi]).compareTo(a[runHi - 1]) >= 0)
runHi++;
}
return runHi - lo;
}
/
//Invert the array within the specified range
private static void reverseRange(Object[] a, int lo, int hi) {
hi--;
while (lo < hi) {
Object t = a[lo];
a[lo++] = a[hi];
a[hi--] = t;
}
}
//Binary insertion sorting is performed on the array in the specified range. At this time, the best method to sort small data is O(nlogn) in time complexity and O(n^2) in space complexity in the worst case
private static void binarySort(Object[] a, int lo, int hi, int start) {
assert lo <= start && start <= hi;
if (start == lo)
start++;
for ( ; start < hi; start++) {
Comparable pivot = (Comparable) a[start];//Transformation from here to strong
// Set left (and right) to the index where a[start] (pivot) belongs
int left = lo;
int right = start;
assert left <= right;
/*
* Invariants:
* pivot >= all in [lo, left).
* pivot < all in [right, start).
*/
while (left < right) {
int mid = (left + right) >>> 1;
if (pivot.compareTo(a[mid]) < 0)//Enter our custom comparison
right = mid;
else
left = mid + 1;
}
assert left == right;
/*
* The invariants still hold: pivot >= all in [lo, left) and
* pivot < all in [left, start), so pivot belongs at left. Note
* that if there are elements equal to pivot, left points to the
* first slot after them -- that's why this sort is stable.
* Slide elements over to make room for pivot.
*/
int n = start - left; // The number of elements to move
// Switch is just an optimization for arraycopy in default case
//The position in the array that needs to be offset
switch (n) {
case 2: a[left + 2] = a[left + 1];
case 1: a[left + 1] = a[left];
break;
default: System.arraycopy(a, left, a, left + 1, n);
}
a[left] = pivot;
}
}
2.2.2 brief introduction to LegacyMergeSort, TimSort and comparable TimSort
hero, how about looking at the source code? Hahaha, this meal is as fierce as a tiger. It can be seen that the more fragrant the tool interface is, the more complex the underlying implementation is! After a brief analysis of the above source code, I think it is necessary to talk about the relevant sorting algorithms. They are encapsulated in LegacyMergeSort, TimSort and comparable TimSort. Let's briefly describe them:
The complexity of MergeSort is O(n^2) for the input that has been sorted in reverse. TimSort is optimized for this situation, including partition merging and optimized processing for reverse and large-scale data. It is a stable sort.
2.3.1 explore the underlying comparison principle of Comparator through a program
public class Test1 {
public static void main(String[] args) throws Exception {
List<Person> list = new ArrayList<>(3);
list.add(new Person("ab",10));
list.add(new Person("ac",3));
list.add(new Person("acd",10));
list.add(new Person("ab",9));
Collections.sort(list, new Comparator<Person>() {
@Override
public int compare(Person o1, Person o2) {
if(!o1.name.equals(o2.name)){
return o1.name.compareTo(o2.name);
}else{
return o1.age-o2.age;
}
}
});
// it's fine too:
//Collections.sort(list,new MyComparator());
System.out.println(list.toString());//[I am ab age: 9, I am ab age: 10, I am ac age: 3, I am acd age: 10]
}
static class MyComparator implements Comparator<Person>{
@Override
public int compare(Person o1, Person o2) {
if(!o1.name.equals(o2.name)){
return o1.name.compareTo(o2.name);
}else{
return o1.age-o2.age;
}
}
}
}
class Person{
String name;
int age;
public Person(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "I am" + name + "Age:"+age ;
}
}
Collections Relevant source code:
public static <T> void sort(List<T> list, Comparator<? super T> c) {
list.sort(c);
}
//
ArrayList Relevant source code:
public void sort(Comparator<? super E> c) {
final int expectedModCount = modCount;
Arrays.sort((E[]) elementData, 0, size, c);//It has been analyzed above and will not be analyzed again
if (modCount != expectedModCount)
throw new ConcurrentModificationException();//It can be seen here that ArrayList is non thread safe. In case of multithreading scenario, concurrent exceptions may be thrown
modCount++;
}
2.3.2 equals of comparator and brief description of other methods
for the unimplemented method equals(obj) in Comparator, let's simply understand: jdk1 8 indicates whether some other object is equal to this Comparator. This method must comply with object General contract for equals (object). In addition, only the specified object is also a Comparator. This method can only return true, and it is in the same order as this Comparator. Therefore, Comp1 Equals (Comp2) means sgn(comp1.compare(o1, o2))==sgn(comp2.compare(o1, o2)) refers to o1 and o2 for each object. Please note that it is always safe not to overwrite object equals(Object) . However, in some cases, overriding this method can improve performance by allowing the program to determine that two different comparators apply the same order. Therefore, it is not necessary to rewrite this method in general, unless in a specific scenario.
the Comparator interface also has several implementation methods, which can return the natural sorting Comparator, forced inversion Comparator, head and tail space friendly Comparator, return the number data type sequence Comparator with the function of extracting the sorting key of a number data type, etc. they all adapt to different demand scenarios, which will not be expanded here. If necessary, you can consult the API documentation or source code.
Supplement: hashCode and equals methods:
- hashCode () is used to obtain hash code, also known as hash value. It returns an integer with high efficiency. The function is to determine the index position in the object.
- equals () is a method in Object. If it is not rewritten, it means to compare the addresses of the two, but. In fact, what we really compare is often the value inside the Object
- Why do hashcodes need equals: hashcodes may have hash conflicts, so the equals of two objects with equal hashcodes may not be equal, but the hashcodes of two objects with equal equals must be equal.
- Common hash algorithms (message digest generated by one-way hash function, key encryption, anti-collision, easy to produce avalanche effect): SHA series, MD5, etc
Supplement: E, T, K, V, N,?, in Java generics Meanings of extends and super:
- E: Element element, used in the collection,
- T: Type is a Java class
- K: Key key
- 5: V alue Value
- N: Number value type
- ?: Uncertain type
- <? Extensions XX >: wildcard character. Unknown class object inherits XX
- <? Super XXX >: wildcard on the. The unknown class object is the super class of XXX
- Use generics at method declarations whose declaration conditions are placed before the return value
public static <T extends Comparable<T>> T fun(T t1,T t2...);
2.4 summary of comparable interface and Comparator interface (dry goods):
Similarly, we will focus on the following points:
- Comparison between the two:
- Both are comparators that can be used to support custom sorting
- The Comparable interface has only one unimplemented method compareTo(T) and only one, while the Comparator interface has two compare(T,T), equals(obj) and multiple methods that return a specific Comparator.
- Comparable is equivalent to an internal Comparator. If this class implements this interface, it indicates that this class has user-defined sorting behavior, while Comparator can be called an external Comparator, which can directly carry out user-defined sorting through anonymous class object classes. Therefore, Comparator embodies a policy mode.
- The Comparable interface is located in Java Lang, and Comparator is located in java,util
- Usage scenario of Comparator interface: sorting and grouping (compare whether two objects belong to the same group)
3: Jdk1 Lamdba expression, functional interface Function, method reference, Stream and Optional classes of 8 features (supplementary)
since some methods in the Comparator mentioned above involve functional interfaces, let's mention some important new features of JDK8 * * [only from the use level] * * (JDK8 allows the interface to have default methods [super base class, super (with parameters) representative object]).
3.1 Lamdba expression
since the expression of Lamdba is relatively simple, let's briefly talk about its syntax expression here:
(parameters) - > expressioin or (parameters) - > {statements;}
features:
- Optional type declaration: it is not necessary to declare parameter types, and the compiler can uniformly identify parameter values
- Optional parameter parentheses: single parameter parentheses can be removed, and multiple parameters must ()
- Optional braces: see if the topic is just a statement
- Return: if the compiler needs to return a brace value, it will automatically return an optional value;
()->"Shen Shuohua talks about programming";
(a,b)-> a+b;
(a,b)-> {return a+b;}
(a,b)-> {System.out.println("I have multiple statements");return a+b;}
public class Test1 {
public static void main(String[] args) throws Exception {
int num = 1;
F f=()->num+"a";//You can't modify num, but you can reference it
System.out.println(f.a());
}
}
interface F{
public Object a();
}
new Thread(()->{}).start();//The internal Lamdba expression overrides the run () method in Runnable
Arrays.sort(list,(a,b)->a-b);//Rewrite the compare(T,T) method of Comparator
be careful:
- Lambda expression is mainly used to define the method type interface executed in the line, for example, a simple method interface (containing only one unimplemented method).
- Lambda expressions avoid the trouble of using anonymous methods and give Java simple but powerful functional programming capabilities
- Local variables defined outside the domain cannot be modified inside the Lamdba expression (accessible), otherwise compilation errors will occur.
- The outer variable referenced by the Lamdba expression may not be modified by final, but it cannot be modified after Lamdba, otherwise a compiler error will be reported
- It is not allowed to declare a parameter or local variable with the same name as a local variable in a Lamdba expression.
3.2 method reference
- Method references point to a method by its name
- Method reference can make the construction of language more compact and concise and reduce redundant code
- Method references use a pair of colons:
usage method:
(1) Object reference:: instance method name
(2) Class name:: static method name
(3) Class name:: instance method name
(4) Class name:: new
(5) Type []: new
public class Test1 {
public static void main(String[] args) throws Exception {
final Person p = Person.create(Person::new,"Zhang San",1);
p.personSay(Person.create(Person::new,"Li Si",21));
Person.staticPersonSay(Person.create(Person::new,"Wang Wu",30));
p.say();
System.out.println(p.toString());
System.out.println("==================");
List<Person> list=new ArrayList<>(4);
list.add(p);
p.setName("Li Si");
list.add(p);//You will find that the first two printed out are Li Si, so here is reference passing, and p points to the same address space
list.add(Person.create(Person::new,"Li Si",21));
list.add(Person.create(Person::new,"Zhang San",1));
list.forEach(System.out::println);
}
}
@FunctionalInterface //This annotation must be marked, functional interface
interface F<T>{//Custom receive two parameters
T get(String name,int age);
}
class Person {
String name;
int age;
public void setName(String name) {
this.name = name;
}
public Person(String name, int age) {
this.name = name;
this.age = age;
}
public static Person create(final F<Person> supplier, String name, int age){
return supplier.get(name,age);
}
public void personSay(final Person person){
System.out.println(this.name+"and"+person.name+"All programmers");
}
public static void staticPersonSay(final Person person){
System.out.println(person.name+"stay heap Lower static");
}
public void say(){
System.out.println(toString());
}
@Override
public String toString() {
return "I am" + name + "Age:"+age ;
}
}
3.3 functional interface
a functional interface is an interface that has only one abstract method, but can have multiple non abstract methods. Functional interfaces can be implicitly converted to lambda expressions. Lambda expressions and method references (actually lambda expressions).
the following example uses the Predicate interface, which is briefly introduced first: the Predicate interface is a functional interface that accepts an input parameter T and returns a boolean result.
public class Test1 {
public static void main(String[] args) throws Exception {
List<Integer> listInt= Arrays.asList(1,2,3,4,5,6,7,8,9);
eval(listInt,i->i%2==0);//2 4 6 8
List<Person> listPerson=Arrays.asList(Person.create(Person::new,"Zhang San",12,"male"),
Person.create(Person::new,"Li Si",21,"female"),
Person.create(Person::new,"Wang Wu",23,"male"));
eval(listPerson,()->"male");
}
public static void eval(List<Integer> list, Predicate<Integer> predicate){
for(Integer i:list){
if(predicate.test(i)){
System.out.print(i+" ");
}
}
System.out.println();
}
public static void eval(List<Person> list,F<Person> personF){
for(Person p:list){
if(personF.get().equals("male")){
System.out.println(p);
}
}
}
}
@FunctionalInterface
interface F<T>{//Custom receive two parameters
String get();
}
@FunctionalInterface
interface Fun<T>{//Custom receive two parameters
T get(String name,int age,String sex);
}
class Person {
String name;
int age;
String sex;
public void setName(String name) {
this.name = name;
}
public Person(String name, int age,String sex) {
this.name = name;
this.age = age;
this.sex=sex;
}
public static Person create(final Fun<Person> supplier, String name, int age,String sex){
return supplier.get(name,age,sex);
}
public void personSay(final Person person){
System.out.println(this.name+"and"+person.name+"All programmers");
}
public static void staticPersonSay(final Person person){
System.out.println(person.name+"stay heap Lower static");
}
public void say(){
System.out.println(toString());
}
@Override
public String toString() {
return "I am" + name + "Age:"+age ;
}
}
Operation results:

common functional interfaces defined in Java include: Consumer represents an operation that accepts an input parameter and returns no return, and function < T, R > accepts an input parameter and returns a result. Predicate accepts an input parameter and returns a boolean result. Supplier has no parameters and returns a result.
3.4 Stream
JDK adds a new abstraction called stream, which allows you to process data in a declarative way. Stream uses an intuitive way similar to querying data from a database with SQL statements to provide a high-level abstraction for the operation and expression of Java collections. Stream API can greatly improve the productivity of Java programmers and make programmers efficient, clean and concise code. This style regards the set of elements to be processed as a stream, which is transmitted in the pipeline and can be processed on the nodes of the pipeline, such as filtering, sorting, aggregation, etc. The element flow is processed by intermediate operations in the pipeline, and finally the previous results are obtained by the final operation.

What is a Stream: a Stream stream is a queue of elements from a data source and supports aggregation operations
- Elements are specific types of objects that form a queue. Stream in Java does not store elements, but calculates on demand
- Data source: it can be set, array, I/O channel, generator, etc
- Aggregation operation: similar to SQL statements, such as filter, map, reduce, find, match, sorted, etc.
Unlike previous Collection operations, Stream operation has two basic features: - Pipelining: all intermediate operations will return the stream object itself. In this way, multiple operations can be connected in series into a pipe, just like the flow style. Doing so optimizes operations, such as delaying laziness and short circuiting
- Internal iteration: in the past, the collection was traversed through Iterator or for each. Explicitly iterating outside the collection is called external iteration. Stream provides a way of internal iteration, which is realized by Visitor mode.
here is a brief reference to the basic principle of visitor mode (some articles on the detailed introduction of common design modes will be written in the future): add an interface to provide visitors to the visited class.
Generate flow: - The collection interface has two methods to generate streams: stream() creates a serial stream for the collection and parallelStream() creates a parallel stream for the collection.
- forEach: stream provides a new method 'forEach' to iterate over each data in the stream.
- Map: the map method is used to map each element to the corresponding result. The following code snippet uses map to output the square corresponding to the element.
- Filter: the filter method is used to filter out elements through the set conditions.
public class Test1 {
public static void main(String[] args) throws Exception {
List<Integer> lists= Arrays.asList(1,2,3,4,5,6,7,8,9);
Random random=new Random();
lists.stream().map(i->i*i*random.nextInt(5)).distinct().filter(list->list%2==0).sorted((Integer o1,Integer o2)->o2-o1).collect(Collectors.toList()).forEach(System.out::println);
}
}
parallel program:
public static void main(String[] args) throws Exception {
List<String> strings = Arrays.asList("Hua", ",", "Bright", "-", "Shen", "+", "chat", "Compile", "Cheng");
strings.parallelStream().filter(string->string.equals("Shen")||string.equals("Bright")||string.equals("Hua")).forEach(System.out::print);
//Shen Shuohua
}
- Collectors, for example, can convert a collection of elements into a string or a collection.
- Statistics: some collectors that produce statistical results are also very useful. They are mainly used for basic types such as int, double and long.
public static void main(String[] args) throws Exception {
List<Integer> lists = Arrays.asList(3,2,2,3,7,3,5);
DoubleSummaryStatistics stats=lists.stream().mapToDouble(i->i*2.0).summaryStatistics();
System.out.println(stats.getAverage());
}
3.5 Optional class
optional class is a nullable container object. If the value exists, isPresent() method will return true, and calling get() method will return the object. Optional is a container: it can hold the value of type T, or just null. Optional provides many useful methods so that we don't need to explicitly control detection. The introduction of optional class solves the null pointer exception well.
public static void main(String[] args) throws Exception {
List<String> strings=Arrays.asList("a","b","ab","Shen Shuohua");
Optional<List<String>> optional=Optional.ofNullable(strings);
optional.stream().map(str->str.contains("Shen Shuohua")).forEach(System.out::println);//true
}
4: Arrays and Collections utility classes
4.1 UML diagram of arrays
Arrays is a tool class for manipulating arrays. Let's first look at its related member properties and four internal classes:
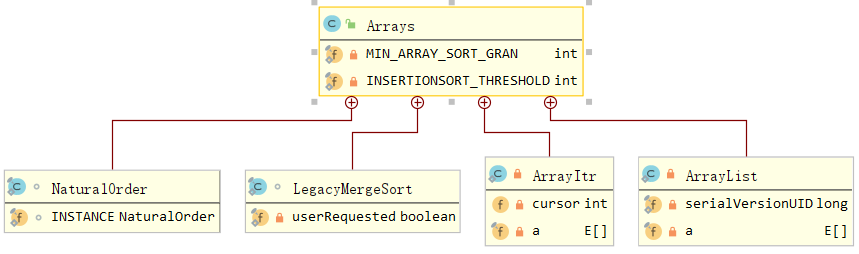
friends, you will find that there is an internal class called ArrayList in Arrays. Why? In fact, it is not surprising, because ArrayList is translated as an array list. An ArrayList itself can call the method toArray() provided by ArrayList to convert it into an array of the corresponding type. Now let's briefly understand the member properties and internal classes of Arrays through the source code:
4.1.1 two constants and internal classes of arrays (source code)
public class Arrays {
//The minimum array length of parallel sorting. Because Arrays involves the method of parallel sorting algorithm, this constant is used by
private static final int MIN_ARRAY_SORT_GRAN = 1 << 13;
//This is an adjustment parameter: the size (threshold) of the list for insertion sorting. It is used for merge sorting first and will be deleted in future versions. Blind guess here is also to be compatible with previous versions
private static final int INSERTIONSORT_THRESHOLD = 7;
private Arrays() {}
//Natural sort comparator (default sort)
static final class NaturalOrder implements Comparator<Object> {
@SuppressWarnings("unchecked")
public int compare(Object first, Object second) {
return ((Comparable<Object>)first).compareTo(second);
}
static final NaturalOrder INSTANCE = new NaturalOrder();
}
//Merge and sort to solve the compatibility with the old version, as mentioned earlier
static final class LegacyMergeSort {
private static final boolean userRequested =
java.security.AccessController.doPrivileged(
new sun.security.action.GetBooleanAction(
"java.util.Arrays.useLegacyMergeSort")).booleanValue();
}
//Array iterator
private static class ArrayItr<E> implements Iterator<E> {
private int cursor;//Cursor, subscript
private final E[] a;//Collection element
ArrayItr(E[] a) {
this.a = a;
}
@Override
public boolean hasNext() {
return cursor < a.length;
}
@Override
public E next() {
int i = cursor;
if (i >= a.length) {
throw new NoSuchElementException();
}
cursor = i + 1;
return a[i];
}
}
//
private static class ArrayList<E> extends AbstractList<E>
implements RandomAccess, java.io.Serializable
{
private static final long serialVersionUID = -2764017481108945198L;
private final E[] a;
ArrayList(E[] array) {
a = Objects.requireNonNull(array);
}
@Override
public int size() {
return a.length;
}
@Override
public Object[] toArray() {
return Arrays.copyOf(a, a.length, Object[].class);
}
@Override
@SuppressWarnings("unchecked") //Tells the compiler to ignore the specified warning and not to display the specified warning message after compilation
public <T> T[] toArray(T[] a) {
int size = size();
if (a.length < size)
return Arrays.copyOf(this.a, size,
(Class<? extends T[]>) a.getClass());
System.arraycopy(this.a, 0, a, 0, size);
if (a.length > size)
a[size] = null;
return a;
}
@Override
public E get(int index) {
return a[index];
}
@Override
public E set(int index, E element) {
E oldValue = a[index];
a[index] = element;
return oldValue;
}
@Override
public int indexOf(Object o) {
E[] a = this.a;
if (o == null) {
for (int i = 0; i < a.length; i++)
if (a[i] == null)
return i;
} else {
for (int i = 0; i < a.length; i++)
if (o.equals(a[i]))
return i;
}
return -1;
}
@Override
public boolean contains(Object o) {
return indexOf(o) >= 0;
}
@Override
public Spliterator<E> spliterator() {
return Spliterators.spliterator(a, Spliterator.ORDERED);
}
@Override
public void forEach(Consumer<? super E> action) {
Objects.requireNonNull(action);
for (E e : a) {
action.accept(e);
}
}
@Override
public void replaceAll(UnaryOperator<E> operator) {
Objects.requireNonNull(operator);
E[] a = this.a;
for (int i = 0; i < a.length; i++) {
a[i] = operator.apply(a[i]);
}
}
@Override
public void sort(Comparator<? super E> c) {
Arrays.sort(a, c);
}
@Override
public Iterator<E> iterator() {
return new ArrayItr<>(a);
}
}
4.1.2 description of relevant interfaces involved
the implementation of RandomAccess interface is generally used for loop traversal, so if this is marked, try to use loop traversal instead of Iterator, because loop traversal will be faster and just act as an identification. Just like ArrayList and LinkedList, starting from the structure of both, ArrayList will use loop traversal speed quickly, and LinkedList will use Iterator speed is not slow.
what is the splitter interface and what is its function: the API in JDK8 explains that it is used to traverse and divide the objects of the elements of the source. The source of the elements covered by the splitter can be, for example, an array, a Collection, an IO channel, or a generator function. The divider can be traversed one by one or in batch. A splitter can also split some of its elements (using trySplit()) into another splitter for use in possible parallel operations. Operations that use an indivisible splitter or operate in a very unbalanced or inefficient manner are unlikely to benefit from parallelism. Penetrating and diverting exhaust elements; Each splitter is only useful for a single batch calculation.
This function can be used as an interface reference or as an expression of the operator function. The only method to be implemented, identity(), always returns the unary operator of its input parameter.
4.1.2 source code analysis of common methods of arrays
Let's look at the following through a procedure:
public class Test1 {
public static void main(String[] args) throws Exception {
Random random=new Random();
int[] a=new int[10];
for(int i=0;i<10;i++) {
a[i] = random.nextInt(100);
}
System.out.println(Arrays.toString(a));
List<Object> intAndString = Arrays.asList(a,new String[]{"a","b"});
for(Object obj:intAndString){
if(obj instanceof int[]){
for(int i:(int[])obj){
System.out.print(i+" ");
}
}
if(obj instanceof String[]){
for(String i:(String[])obj){
System.out.print(i+" ");
}
}
}
Object[] objArr=intAndString.toArray();//Want to traverse, the same as above
Arrays.sort(a);
Arrays.stream(a).filter(i->i%2==0).forEach(System.out::print);
System.out.println();
//Equality is 0 and inequality is 1
Syst/em.out.println(Arrays.compare(a,new int[]{1,2,3}));
System.out.println(Arrays.hashCode(a));
System.out.println(12+"Location:"+Arrays.binarySearch(new int[]{8,10,1,9,12,20,33,80,7},12));
Arrays.compareUnsigned(a,new int[]{random.nextInt(1000),random.nextInt(10),random.nextInt(100)});
char[] charArr=Arrays.copyOf((new char[]{(char)random.nextInt(100),(char)random.nextInt(100),(char)random.nextInt(100)}),4);
Arrays.parallelSort(charArr);
for(char c:charArr){
System.out.print(c+" ");
}
System.out.println();
Arrays.mismatch(a,0,2,new int[]{10,11,12},0,3);
Spliterator.OfInt spliterator = Arrays.spliterator(a);
spliterator.forEachRemaining(new Consumer<Integer>() {
@Override
public void accept(Integer integer) {
if(integer%2==0){
integer*=integer;
}
System.out.print(integer+",");
}
});
}
}
Random data retrieval is used in some parts of the above code, so the results of each run are not necessarily the same. Therefore, the following is the results of a run:

Let's take a look at the source code:
public static String toString(int[] a) {
if (a == null)
return "null";
int iMax = a.length - 1;
if (iMax == -1)
return "[]";
StringBuilder b = new StringBuilder();//Note that StringBuilder is used for stringing,
b.append('[');
for (int i = 0; ; i++) {
b.append(a[i]);
if (i == iMax)
return b.append(']').toString();//It's here. return
b.append(", ");
}
}
///
public static <T> List<T> asList(T... a) {
return new ArrayList<>(a);//This uses its inner class
}
ArrayList(E[] array) {
a = Objects.requireNonNull(array);
}
public static <T> T requireNonNull(T obj) {
if (obj == null)
throw new NullPointerException();
return obj;
}
///
public Object[] toArray() {
return Arrays.copyOf(a, a.length, Object[].class);
}
@HotSpotIntrinsicCandidate //As noted by the annotation, there is a set of efficient implementation in HotSpot. The efficient implementation is based on CPU instructions. When running, the efficient implementation of HotSpot maintenance will replace the source implementation of JDK, so as to obtain more efficient efficiency
public static <T,U> T[] copyOf(U[] original, int newLength, Class<? extends T[]> newType) {
@SuppressWarnings("unchecked")
T[] copy = ((Object)newType == (Object)Object[].class)//Determine the array type and make corresponding operations
? (T[]) new Object[newLength]
: (T[]) Array.newInstance(newType.getComponentType(), newLength);
System.arraycopy(original, 0, copy, 0,
Math.min(original.length, newLength));
return copy;
}
//native modification is implemented by the underlying C
@HotSpotIntrinsicCandidate
public static native void arraycopy(Object src, int srcPos,
Object dest, int destPos,
int length);
//
public static void sort(int[] a) {
DualPivotQuicksort.sort(a, 0, a.length - 1, null, 0, 0);//Quick sort is used here
}
Source code analysis of double benchmark quick sorting algorithm
Double benchmark quick sorting algorithm: (because the source code is too long, small partners who can't understand it for the time being can skip it. In fact, the idea is to match and sort according to the best use scenarios of several basic sorting algorithms of our data structure)
final class DualPivotQuicksort {
private DualPivotQuicksort() {}
//Maximum number of runs of merge sort
private static final int MAX_RUN_COUNT = 67;
//If the sort length is less than this value, quick sort is preferred to merge sort
private static final int QUICKSORT_THRESHOLD = 286;
//Less than this value, insert sort takes precedence over quick sort
private static final int INSERTION_SORT_THRESHOLD = 47;
//If greater than this value, the count sort takes precedence over the insert sort
private static final int COUNTING_SORT_THRESHOLD_FOR_BYTE = 29;
//If it is greater than this value, the counting sort takes precedence over the quick sort
private static final int COUNTING_SORT_THRESHOLD_FOR_SHORT_OR_CHAR = 3200;
static void sort(int[] a, int left, int right,
int[] work, int workBase, int workLen) {
// Use Quicksort on small arrays
if (right - left < QUICKSORT_THRESHOLD) {
sort(a, left, right, true);
return;
}
/*
* Index run[i] is the start of i-th run
* (ascending or descending sequence).
*/
int[] run = new int[MAX_RUN_COUNT + 1];
int count = 0; run[0] = left;
// Check if the array is nearly sorted
for (int k = left; k < right; run[count] = k) {
// Equal items in the beginning of the sequence
while (k < right && a[k] == a[k + 1])
k++;
if (k == right) break; // Sequence finishes with equal items
if (a[k] < a[k + 1]) { // ascending
while (++k <= right && a[k - 1] <= a[k]);
} else if (a[k] > a[k + 1]) { // descending
while (++k <= right && a[k - 1] >= a[k]);
// Transform into an ascending sequence
for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {
int t = a[lo]; a[lo] = a[hi]; a[hi] = t;
}
}
// Merge a transformed descending sequence followed by an
// ascending sequence
if (run[count] > left && a[run[count]] >= a[run[count] - 1]) {
count--;
}
/*
* The array is not highly structured,
* use Quicksort instead of merge sort.
*/
if (++count == MAX_RUN_COUNT) {
sort(a, left, right, true);
return;
}
}
// These invariants should hold true:
// run[0] = 0
// run[<last>] = right + 1; (terminator)
if (count == 0) {
// A single equal run
return;
} else if (count == 1 && run[count] > right) {
// Either a single ascending or a transformed descending run.
// Always check that a final run is a proper terminator, otherwise
// we have an unterminated trailing run, to handle downstream.
return;
}
right++;
if (run[count] < right) {
// Corner case: the final run is not a terminator. This may happen
// if a final run is an equals run, or there is a single-element run
// at the end. Fix up by adding a proper terminator at the end.
// Note that we terminate with (right + 1), incremented earlier.
run[++count] = right;
}
// Determine alternation base for merge
byte odd = 0;
for (int n = 1; (n <<= 1) < count; odd ^= 1);
// Use or create temporary array b for merging
int[] b; // temp array; alternates with a
int ao, bo; // array offsets from 'left'
int blen = right - left; // space needed for b
if (work == null || workLen < blen || workBase + blen > work.length) {
work = new int[blen];
workBase = 0;
}
if (odd == 0) {
System.arraycopy(a, left, work, workBase, blen);
b = a;
bo = 0;
a = work;
ao = workBase - left;
} else {
b = work;
ao = 0;
bo = workBase - left;
}
// Merging
for (int last; count > 1; count = last) {
for (int k = (last = 0) + 2; k <= count; k += 2) {
int hi = run[k], mi = run[k - 1];
for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {
if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {
b[i + bo] = a[p++ + ao];
} else {
b[i + bo] = a[q++ + ao];
}
}
run[++last] = hi;
}
if ((count & 1) != 0) {
for (int i = right, lo = run[count - 1]; --i >= lo;
b[i + bo] = a[i + ao]
);
run[++last] = right;
}
int[] t = a; a = b; b = t;
int o = ao; ao = bo; bo = o;
}
}
/
private static void sort(int[] a, int left, int right, boolean leftmost) {
int length = right - left + 1;
// Use insertion sort on tiny arrays
if (length < INSERTION_SORT_THRESHOLD) {
if (leftmost) {
/*
* Traditional (without sentinel) insertion sort,
* optimized for server VM, is used in case of
* the leftmost part.
*/
for (int i = left, j = i; i < right; j = ++i) {
int ai = a[i + 1];
while (ai < a[j]) {
a[j + 1] = a[j];
if (j-- == left) {
break;
}
}
a[j + 1] = ai;
}
} else {
/*
* Skip the longest ascending sequence.
*/
do {
if (left >= right) {
return;
}
} while (a[++left] >= a[left - 1]);
/*
* Every element from adjoining part plays the role
* of sentinel, therefore this allows us to avoid the
* left range check on each iteration. Moreover, we use
* the more optimized algorithm, so called pair insertion
* sort, which is faster (in the context of Quicksort)
* than traditional implementation of insertion sort.
*/
for (int k = left; ++left <= right; k = ++left) {
int a1 = a[k], a2 = a[left];
if (a1 < a2) {
a2 = a1; a1 = a[left];
}
while (a1 < a[--k]) {
a[k + 2] = a[k];
}
a[++k + 1] = a1;
while (a2 < a[--k]) {
a[k + 1] = a[k];
}
a[k + 1] = a2;
}
int last = a[right];
while (last < a[--right]) {
a[right + 1] = a[right];
}
a[right + 1] = last;
}
return;
}
// Inexpensive approximation of length / 7
int seventh = (length >> 3) + (length >> 6) + 1;
/*
* Sort five evenly spaced elements around (and including) the
* center element in the range. These elements will be used for
* pivot selection as described below. The choice for spacing
* these elements was empirically determined to work well on
* a wide variety of inputs.
*/
int e3 = (left + right) >>> 1; // The midpoint
int e2 = e3 - seventh;
int e1 = e2 - seventh;
int e4 = e3 + seventh;
int e5 = e4 + seventh;
// Sort these elements using insertion sort
if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; }
if (a[e3] < a[e2]) { int t = a[e3]; a[e3] = a[e2]; a[e2] = t;
if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
}
if (a[e4] < a[e3]) { int t = a[e4]; a[e4] = a[e3]; a[e3] = t;
if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
}
}
if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t;
if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t;
if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
}
}
}
// Pointers
int less = left; // The index of the first element of center part
int great = right; // The index before the first element of right part
if (a[e1] != a[e2] && a[e2] != a[e3] && a[e3] != a[e4] && a[e4] != a[e5]) {
/*
* Use the second and fourth of the five sorted elements as pivots.
* These values are inexpensive approximations of the first and
* second terciles of the array. Note that pivot1 <= pivot2.
*/
int pivot1 = a[e2];
int pivot2 = a[e4];
/*
* The first and the last elements to be sorted are moved to the
* locations formerly occupied by the pivots. When partitioning
* is complete, the pivots are swapped back into their final
* positions, and excluded from subsequent sorting.
*/
a[e2] = a[left];
a[e4] = a[right];
/*
* Skip elements, which are less or greater than pivot values.
*/
while (a[++less] < pivot1);
while (a[--great] > pivot2);
/*
* Partitioning:
*
* left part center part right part
* +--------------------------------------------------------------+
* | < pivot1 | pivot1 <= && <= pivot2 | ? | > pivot2 |
* +--------------------------------------------------------------+
* ^ ^ ^
* | | |
* less k great
*
* Invariants:
*
* all in (left, less) < pivot1
* pivot1 <= all in [less, k) <= pivot2
* all in (great, right) > pivot2
*
* Pointer k is the first index of ?-part.
*/
outer:
for (int k = less - 1; ++k <= great; ) {
int ak = a[k];
if (ak < pivot1) { // Move a[k] to left part
a[k] = a[less];
/*
* Here and below we use "a[i] = b; i++;" instead
* of "a[i++] = b;" due to performance issue.
*/
a[less] = ak;
++less;
} else if (ak > pivot2) { // Move a[k] to right part
while (a[great] > pivot2) {
if (great-- == k) {
break outer;
}
}
if (a[great] < pivot1) { // a[great] <= pivot2
a[k] = a[less];
a[less] = a[great];
++less;
} else { // pivot1 <= a[great] <= pivot2
a[k] = a[great];
}
/*
* Here and below we use "a[i] = b; i--;" instead
* of "a[i--] = b;" due to performance issue.
*/
a[great] = ak;
--great;
}
}
// Swap pivots into their final positions
a[left] = a[less - 1]; a[less - 1] = pivot1;
a[right] = a[great + 1]; a[great + 1] = pivot2;
// Sort left and right parts recursively, excluding known pivots
sort(a, left, less - 2, leftmost);
sort(a, great + 2, right, false);
/*
* If center part is too large (comprises > 4/7 of the array),
* swap internal pivot values to ends.
*/
if (less < e1 && e5 < great) {
/*
* Skip elements, which are equal to pivot values.
*/
while (a[less] == pivot1) {
++less;
}
while (a[great] == pivot2) {
--great;
}
/*
* Partitioning:
*
* left part center part right part
* +----------------------------------------------------------+
* | == pivot1 | pivot1 < && < pivot2 | ? | == pivot2 |
* +----------------------------------------------------------+
* ^ ^ ^
* | | |
* less k great
*
* Invariants:
*
* all in (*, less) == pivot1
* pivot1 < all in [less, k) < pivot2
* all in (great, *) == pivot2
*
* Pointer k is the first index of ?-part.
*/
outer:
for (int k = less - 1; ++k <= great; ) {
int ak = a[k];
if (ak == pivot1) { // Move a[k] to left part
a[k] = a[less];
a[less] = ak;
++less;
} else if (ak == pivot2) { // Move a[k] to right part
while (a[great] == pivot2) {
if (great-- == k) {
break outer;
}
}
if (a[great] == pivot1) { // a[great] < pivot2
a[k] = a[less];
/*
* Even though a[great] equals to pivot1, the
* assignment a[less] = pivot1 may be incorrect,
* if a[great] and pivot1 are floating-point zeros
* of different signs. Therefore in float and
* double sorting methods we have to use more
* accurate assignment a[less] = a[great].
*/
a[less] = pivot1;
++less;
} else { // pivot1 < a[great] < pivot2
a[k] = a[great];
}
a[great] = ak;
--great;
}
}
}
// Sort center part recursively
sort(a, less, great, false);
} else { // Partitioning with one pivot
/*
* Use the third of the five sorted elements as pivot.
* This value is inexpensive approximation of the median.
*/
int pivot = a[e3];
/*
* Partitioning degenerates to the traditional 3-way
* (or "Dutch National Flag") schema:
*
* left part center part right part
* +-------------------------------------------------+
* | < pivot | == pivot | ? | > pivot |
* +-------------------------------------------------+
* ^ ^ ^
* | | |
* less k great
*
* Invariants:
*
* all in (left, less) < pivot
* all in [less, k) == pivot
* all in (great, right) > pivot
*
* Pointer k is the first index of ?-part.
*/
for (int k = less; k <= great; ++k) {
if (a[k] == pivot) {
continue;
}
int ak = a[k];
if (ak < pivot) { // Move a[k] to left part
a[k] = a[less];
a[less] = ak;
++less;
} else { // a[k] > pivot - Move a[k] to right part
while (a[great] > pivot) {
--great;
}
if (a[great] < pivot) { // a[great] <= pivot
a[k] = a[less];
a[less] = a[great];
++less;
} else { // a[great] == pivot
/*
* Even though a[great] equals to pivot, the
* assignment a[k] = pivot may be incorrect,
* if a[great] and pivot are floating-point
* zeros of different signs. Therefore in float
* and double sorting methods we have to use
* more accurate assignment a[k] = a[great].
*/
a[k] = pivot;
}
a[great] = ak;
--great;
}
}
/*
* Sort left and right parts recursively.
* All elements from center part are equal
* and, therefore, already sorted.
*/
sort(a, left, less - 1, leftmost);
sort(a, great + 1, right, false);
}
}
The above is the first part of the first mock exam algorithm. We can not get too entangled. The last module will put the code of our several basic sorting algorithms.
I'm sorry, everyone. I wanted to catch up with the source code of the obscene aspect, but I was dizzy. Those who have the ability to look it up on their own. My little brother, I have limited ability at present. I can understand it in the future and will supplement and publish it. Let's take a look at the related to compare and hashcode:
public static int compare(int[] a, int[] b) {
if (a == b)
return 0;
if (a == null || b == null)
return a == null ? -1 : 1;
int i = ArraysSupport.mismatch(a, b,
Math.min(a.length, b.length));
if (i >= 0) {
return Integer.compare(a[i], b[i]);
}
return a.length - b.length;
}
public static int mismatch(int[] a,
int[] b,
int length) {
int i = 0;
if (length > 1) {
if (a[0] != b[0])
return 0;
i = vectorizedMismatch(
a, Unsafe.ARRAY_INT_BASE_OFFSET,
b, Unsafe.ARRAY_INT_BASE_OFFSET,
length, LOG2_ARRAY_INT_INDEX_SCALE);
if (i >= 0)
return i;
i = length - ~i;
}
for (; i < length; i++) {
if (a[i] != b[i])
return i;
}
return -1;
}
public static int hashCode(int a[]) {
if (a == null)
return 0;
int result = 1;
for (int element : a)
result = 31 * result + element;//Using sub hash algorithm
return result;
}
Binary search algorithm:
public static int binarySearch(int[] a, int key) {
return binarySearch0(a, 0, a.length, key);
}
private static int binarySearch0(int[] a, int fromIndex, int toIndex,
int key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
int mid = (low + high) >>> 1;//The middle bit is more efficient
int midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
//The numeric processing element is unsigned
/**
If two arrays share a prefix, the comparison is the result of comparing two elements. Otherwise, if an array is the correct prefix of another array, the results of comparing the lengths of the two arrays will be lexicographically
*/
public static int compareUnsigned(int[] a, int[] b) {
if (a == b)
return 0;
if (a == null || b == null)
return a == null ? -1 : 1;
int i = ArraysSupport.mismatch(a, b,
Math.min(a.length, b.length));
if (i >= 0) {
return Integer.compareUnsigned(a[i], b[i]);
}
return a.length - b.length;
}
///
public static void parallelSort(int[] a) {
int n = a.length, p, g;
//If the array size is less than the threshold or the processor has only one core
if (n <= MIN_ARRAY_SORT_GRAN ||
(p = ForkJoinPool.getCommonPoolParallelism()) == 1)
DualPivotQuicksort.sort(a, 0, n - 1, null, 0, 0);
else//Otherwise, the array can be split into multiple sub arrays to perform sorting and merging in parallel (pool principle)
new ArraysParallelSortHelpers.FJInt.Sorter
(null, a, new int[n], 0, n, 0,
((g = n / (p << 2)) <= MIN_ARRAY_SORT_GRAN) ?
MIN_ARRAY_SORT_GRAN : g).invoke();
}
4.1.3 brief description of double benchmark quick sort method DualPivotQuickSort
DualPivotQuickSort is the optimization of classic quicksort. We will summarize the classic quicksort below. The double benchmark here is different from quicksort. In the actual working process, it does not directly sort any incoming array, but will first conduct a series of tests on the array, and then select the most suitable algorithm to sort according to the actual situation.
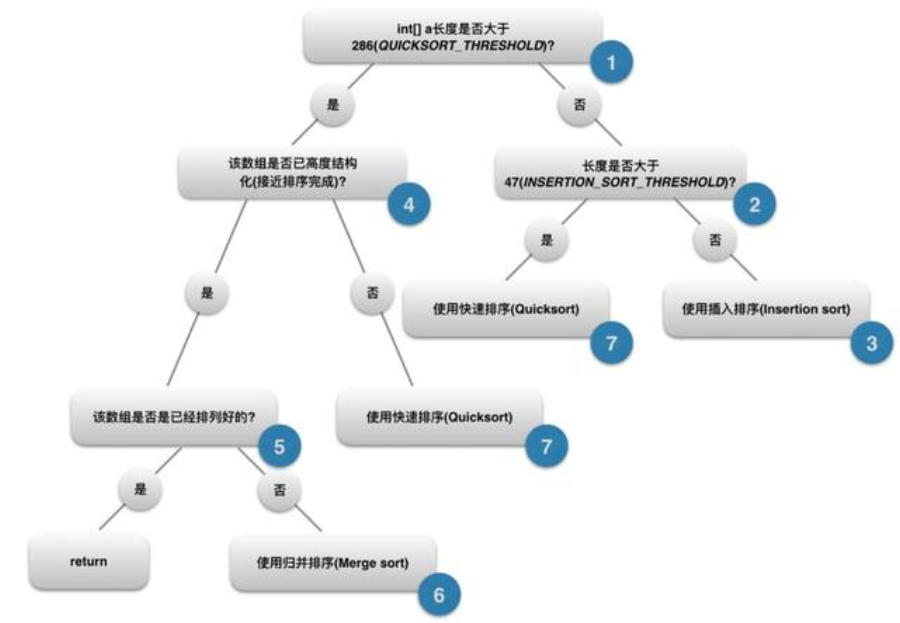
4.1.4 summary of arrays:
The key points are as follows:
- The sort method of Arrays adopts the design idea of policy pattern. The design idea of policy pattern is to define algorithm families (policy groups) and package them respectively to replace each other. This pattern makes the transformation of algorithm independent of the customers using the algorithm.
- Arrays. The List instance object returned by the aslist () method cannot be added or deleted, and will report Java Lang.unsupportedoperationexception exception (because the array object encapsulated at the bottom is final modified), but it still has the characteristics of ArrayList. You don't need to modify it.
- The difference between parallelSort and sort methods: the former provides the function of parallel operation, that is, if the array size is greater than the threshold and the processor is multi-core, the array can be divided into multiple sub arrays (ForkJoin pool support is provided), sorted and merged respectively. It is suitable for the scenario of large amount of data and multi-core computer, while sort is the opposite.
4.2 Collections
because there are a lot of related methods, member properties and internal classes of Collections, I won't list them one by one here.
4.2.1 check the source code of common methods of Collections through a program
public class Test1 {
public static void main(String[] args) throws Exception {
List<String> list = Arrays.asList("a", "c", "b");//The returned list cannot be modified
List<Integer> list1=new ArrayList<>();
for(int i=0;i<10;i++){
list1.add(i);
}
Iterator<Object> objectIterator = Collections.emptyIterator();//The object iterator returned is immutable
Collections.reverse(list1);
list1.stream().forEach(System.out::print);
System.out.println();
Map<UUID,String> hashMap=new HashMap<>();
for(int i=0;i<10;i++){
hashMap.put(UUID.randomUUID(), "I am" + i);
}
List<Map.Entry<UUID,String>> list2=new ArrayList<>();
for(Map.Entry<UUID,String> entry:hashMap.entrySet()){
list2.add(entry);
}
Comparator<Map.Entry<UUID, String>> comparator=new Comparator<Map.Entry<UUID, String>>() {
@Override
public int compare(Map.Entry<UUID, String> o1, Map.Entry<UUID, String> o2) {
String str1=o1.getValue();
String str2=o2.getValue();
int a=Integer.valueOf(String.valueOf(str1.charAt(str1.length()-1)));
int b=Integer.valueOf(String.valueOf(str2.charAt(str2.length()-1)));
return a-b;
}
};
Collections.sort(list2, comparator);
System.out.println("After sorting:");
for(Map.Entry<UUID,String> entry:list2){
System.out.println(entry.getKey()+":"+entry.getValue());
}
Map<UUID, String> uuidStringMap = Collections.checkedMap(hashMap, UUID.class, String.class);//checkedXXX returns the security view of XXX
System.out.println("Security view:");
for(Map.Entry<UUID,String> entry:uuidStringMap.entrySet()){
System.out.println(entry.getKey()+":"+entry.getValue());
}
Collection<String> collection=new ArrayList<>(),collection1=new ArrayList<>();
for(int i=0;i<10;i++){
if(i%2==0){
collection.add("Shen Shuohua");
collection1.add("Shen Shuohua");
}else{
collection.add("Programming chat");
collection1.add("programmer");
}
}
System.out.println(Collections.disjoint(collection1,collection));
Collections.shuffle(list,new Random());//Randomly shuffle the list using the specified random source
Collections.swap(list,0,1);
List<Integer> list3 = Collections.synchronizedList(list1);//Return thread safe list
Map<UUID, String> uuidStringMap1 = Collections.unmodifiableMap(hashMap);//Returns a view map that cannot be modified
List<Integer> es = Collections.checkedList(new ArrayList<Integer>(), Integer.class);
}
}
The operation results are as follows:

Part of the source code is as follows:
@SafeVarargs
@SuppressWarnings("varargs")
public static <T> List<T> asList(T... a) {
return new ArrayList<>(a);
}
private final E[] a;
ArrayList(E[] array) {
a = Objects.requireNonNull(array);
}
static final EmptyIterator<Object> EMPTY_ITERATOR
public static <T> Iterator<T> emptyIterator() {
return (Iterator<T>) EmptyIterator.EMPTY_ITERATOR;
}
public static void reverse(List<?> list) {
int size = list.size();
if (size < REVERSE_THRESHOLD || list instanceof RandomAccess) {//Judge whether it is less than the threshold or whether the list inherits the RandomAccess interface
for (int i=0, mid=size>>1, j=size-1; i<mid; i++, j--)//I admire this way of writing
swap(list, i, j);
} else {
ListIterator fwd = list.listIterator();
ListIterator rev = list.listIterator(size);
for (int i=0, mid=list.size()>>1; i<mid; i++) {
Object tmp = fwd.next();
fwd.set(rev.previous());
rev.set(tmp);
}
}
}
/
public static boolean disjoint(Collection<?> c1, Collection<?> c2) {
Collection<?> contains = c2;
Collection<?> iterate = c1;
if (c1 instanceof Set) {
iterate = c2;
contains = c1;
} else if (!(c2 instanceof Set)) {
int c1size = c1.size();
int c2size = c2.size();
if (c1size == 0 || c2size == 0) {
return true;
}
if (c1size > c2size) {
iterate = c2;
contains = c1;
}
}
for (Object e : iterate) {
if (contains.contains(e)) {//If two sets have common elements, return false
return false;
}
}
return true;
}
///
public static void shuffle(List<?> list, Random rnd) {//Random scrambling according to the specified random source
int size = list.size();
if (size < SHUFFLE_THRESHOLD || list instanceof RandomAccess) {
for (int i=size; i>1; i--)
swap(list, i-1, rnd.nextInt(i));
} else {
Object arr[] = list.toArray();
// Shuffle array
for (int i=size; i>1; i--)
swap(arr, i-1, rnd.nextInt(i));
// Dump array back into list
// instead of using a raw type here, it's possible to capture
// the wildcard but it will require a call to a supplementary
// private method
ListIterator it = list.listIterator();
for (Object e : arr) {
it.next();
it.set(e);
}
}
}
public static <T> List<T> synchronizedList(List<T> list) {
return (list instanceof RandomAccess ?
new SynchronizedRandomAccessList<>(list) :
new SynchronizedList<>(list));
}
SynchronizedRandomAccessList(List<E> list) {
super(list);
}
SynchronizedList(List<E> list) {
super(list);
this.list = list;
}
//Forcibly lock the properties and methods of each member
static class SynchronizedCollection<E> implements Collection<E>, Serializable {
private static final long serialVersionUID = 3053995032091335093L;
final Collection<E> c; // Backing Collection
final Object mutex; // Object on which to synchronize
SynchronizedCollection(Collection<E> c) {
this.c = Objects.requireNonNull(c);
mutex = this;
}
SynchronizedCollection(Collection<E> c, Object mutex) {
this.c = Objects.requireNonNull(c);
this.mutex = Objects.requireNonNull(mutex);
}
public int size() {
synchronized (mutex) {return c.size();}
}
public boolean isEmpty() {
synchronized (mutex) {return c.isEmpty();}
}
public boolean contains(Object o) {
synchronized (mutex) {return c.contains(o);}
}
public Object[] toArray() {
synchronized (mutex) {return c.toArray();}
}
public <T> T[] toArray(T[] a) {
synchronized (mutex) {return c.toArray(a);}
}
public <T> T[] toArray(IntFunction<T[]> f) {
synchronized (mutex) {return c.toArray(f);}
}
public Iterator<E> iterator() {
return c.iterator(); //Synchronization must be done manually by the user
}
public boolean add(E e) {
synchronized (mutex) {return c.add(e);}
}
public boolean remove(Object o) {
synchronized (mutex) {return c.remove(o);}
}
public boolean containsAll(Collection<?> coll) {
synchronized (mutex) {return c.containsAll(coll);}
}
public boolean addAll(Collection<? extends E> coll) {
synchronized (mutex) {return c.addAll(coll);}
}
public boolean removeAll(Collection<?> coll) {
synchronized (mutex) {return c.removeAll(coll);}
}
public boolean retainAll(Collection<?> coll) {
synchronized (mutex) {return c.retainAll(coll);}
}
public void clear() {
synchronized (mutex) {c.clear();}
}
public String toString() {
synchronized (mutex) {return c.toString();}
}
// Override default methods in Collection
@Override
public void forEach(Consumer<? super E> consumer) {
synchronized (mutex) {c.forEach(consumer);}
}
@Override
public boolean removeIf(Predicate<? super E> filter) {
synchronized (mutex) {return c.removeIf(filter);}
}
@Override
public Spliterator<E> spliterator() {
return c.spliterator(); //Synchronization must be done manually by the user
}
@Override
public Stream<E> stream() {
return c.stream(); //Synchronization must be done manually by the user
}
@Override
public Stream<E> parallelStream() {
return c.parallelStream(); // Synchronization must be done manually by the user
}
private void writeObject(ObjectOutputStream s) throws IOException {
synchronized (mutex) {s.defaultWriteObject();}
}
}
///
public static <E> List<E> checkedList(List<E> list, Class<E> type) {
return (list instanceof RandomAccess ?
new CheckedRandomAccessList<>(list, type) :
new CheckedList<>(list, type));
}
CheckedRandomAccessList(List<E> list, Class<E> type) {
super(list, type);
}
CheckedList(List<E> list, Class<E> type) {
super(list, type);
this.list = list;
}
CheckedCollection(Collection<E> c, Class<E> type) {
this.c = Objects.requireNonNull(c, "c");
this.type = Objects.requireNonNull(type, "type");
}
public static Integer valueOf(int i) {
if (i >= IntegerCache.low && i <= IntegerCache.high)
return IntegerCache.cache[i + (-IntegerCache.low)];
return new Integer(i);
}
Integer:
public boolean add(E e) { return c.add(typeCheck(e)); }
//Here are the key points: each time you need to add an operation, it will judge whether it is value or the specified type
E typeCheck(Object o) {
if (o != null && !type.isInstance(o))
throw new ClassCastException(badElementMsg(o));
return (E) o;
}
Collections.sort(list,comparator):
public static <T> void sort(List<T> list, Comparator<? super T> c) {
list.sort(c);
}
default void sort(Comparator<? super E> c) {
Object[] a = this.toArray();
Arrays.sort(a, (Comparator) c);
ListIterator<E> i = this.listIterator();
for (Object e : a) {
i.next();
i.set((E) e);
}
}
public static <T> void sort(T[] a, Comparator<? super T> c) {
if (c == null) {
sort(a);
} else {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, c);
else
TimSort.sort(a, 0, a.length, c, null, 0, 0);
}
}
4.2.2Collections summary
The key points are as follows:
- Difference between Collection and Collections: (according to the Collection framework diagram)
- Collection is the interface of the collection framework and provides general interface methods for basic operations on collection objects. Of course, there are also specific implementations
- Collections is a wrapper class (tool class) that cannot be instantiated and contains static polymorphic methods related to collection operations (search, sorting, thread safety, etc.).
- The tim sort element is also mentioned above.
- Collections. Differences between sysnchronizedlist and CopyOnWriteArrayList:
- Collections.sysnchronizedList: when multithreading concurrency is large, the performance of read operation is not as good as CopyOnWrite.
- CopyOnWriteArrayList: literally, it means copying a new one. When there is a large amount of multithreading concurrency, if it is used for write operations, the performance will be greatly affected.
- The difference between parallelism and Concurrency: parallelism means that multiple CPUs execute multiple tasks (threads) at the same time [improvement of hardware equipment], and concurrency means that a single CPU executes multiple tasks in the same time period (concurrent execution algorithm: such as polling)
- Collections.checkedXXX: when executing the stored data type for XXX set type, this set can store various data types, but if this method is formulated for XXX set, XXX will check whether the data type of operation is the specified data type at run time.
List list=new ArrayList();
list.add(1);
list.add("a");
List list1 = Collections.checkedList(list, String.class);//The above operation is OK
//However, if the returned list1 is used to insert a non specified data type, an error will be reported
list1.add(1);//java.lang.ClassCastException:
5: Sorting and searching of data structures and algorithms
5.1 eight basic sorting algorithms
Sorting is divided into internal sorting and external sorting:
- There are eight categories of internal sorting: direct insertion sort, Hill sort, simple selection sort, heap sort, bubble sort, quick sort, merge sort and cardinal sort
- There are two types of external sorting: counting sorting and bucket sorting
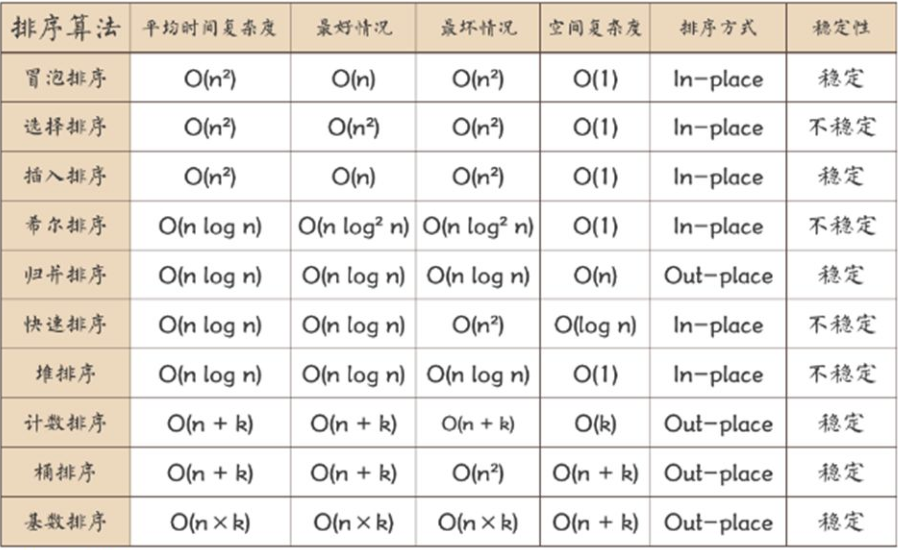
Here's the code I've written before:
5.1.1 direct insertion sort
public static void insertedSort(int[] arr) {
int tmp, index;
for (int i = 1; i < arr.length; i++) {
tmp = arr[i];
index = i - 1;
// Ascending order
while (index >= 0 && tmp < arr[index]) {// Move back if it's bigger than tmp
arr[index + 1] = arr[index];
index--;
}
if (index != i - 1)
arr[index + 1] = tmp;
}
}
5.1.2 Hill sorting
public static void swapShellSort(int[] arr) {
int tmp;
for (int gap = arr.length / 2; gap > 2; gap /= 2) {//pace
for (int i = gap; i < arr.length; i++) {
for (int j = i - gap; j >= 0; j -= gap) {
if (arr[j] > arr[j + gap]) {
tmp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = tmp;
}
}
}
}
}
///
public static void shiftShellSort(int[] arr) {
int tmp;
for (int gap = arr.length / 2; gap > 2; gap /= 2) {// pace
for (int i = gap; i < arr.length; i++) {
int j = i;
tmp = arr[j];
if (tmp < arr[j - gap]) {
while (j - gap >= 0 && tmp < arr[j - gap]) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = tmp;
}
}
}
}
5.1.3 simple selection sorting
public static void selectedSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
int index = i, min = arr[i];
for (int j = i + 1; j < arr.length; j++) {
if (min > arr[j]) {
min = arr[j];
index = j;
}
}
if (index != i) {
arr[index] = arr[i];
arr[i] = min;
}
}
}
5.1.4 heap sorting
//Using arrays to simulate heap sorting
public static void heapSort(int[] arr) {
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, arr.length);
}
int tmp;
for (int i = arr.length - 1; i > 0; i--) {
tmp = arr[i];
arr[i] = arr[0];
arr[0] = tmp;
adjustHeap(arr, 0, i);
}
}
// Maximum heap
public static void adjustHeap(int[] arr, int notLeafIndex, int len) {
int tmp = arr[notLeafIndex];
for (int i = notLeafIndex * 2 + 1; i < len; i = i * 2 + 1) {
if (i + 1 < len && arr[i] < arr[i + 1]) {
i++;
}
if (arr[i] > tmp) {
arr[notLeafIndex] = arr[i];
notLeafIndex = i;
} else {
break;
}
}
arr[notLeafIndex] = tmp;
}
5.1.5 bubble sorting
public static void bubbleSort(int[] arr) {
boolean flag = false;
int tmp = 0;
for (int i = 0; i < arr.length && !flag; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = true;
}
}
if (flag)
flag = true;
}
}
5.1.6 quick sort
public static void quickSort(int[] arr, int left, int right) {
int l = left, r = right;
//int midIndexVal = arr[r - (r - l) / 2];
int midIndexVal = arr[(right+left)>>>2];
int tmp = 0;
while (l < r) {
while (arr[l] < midIndexVal) {
l++;
}
while (arr[r] > midIndexVal) {
r--;
}
if (l >= r)
break;
tmp = arr[l];
arr[l] = arr[r];
arr[r] = tmp;
if (arr[l] == midIndexVal)
r--;
if (arr[r] == midIndexVal)
l++;
if(l==r) {//Prevent OutOfStack
l++;
r--;
}
if(left<r)
quickSort(arr, left, r);
if(l<right)
quickSort(arr, l, right);
}
}
5.1.7 merge sort
public static void mergeSort(int[] arr, int left, int right, int[] tmp) {
// int midIndex = arr[r - (r - l) / 2];
int midIndex = arr[(right + left) >>> 2];
mergeSort(arr, left, midIndex, tmp);
mergeSort(arr, midIndex, right, tmp);
merge(arr, left, midIndex, right, tmp);
}
public static void merge(int[] arr, int left, int midIndex, int right, int[] tmp) {
int l = left, r = midIndex + 1, cur = 0;
while (l <= midIndex && r <= right) {
if (arr[l] <= arr[r]) {
tmp[cur] = arr[l];
l++;
cur++;
} else {
tmp[cur] = arr[r];
r++;
cur++;
}
}
while (l <= midIndex) {
tmp[cur++] = arr[l++];
}
while (r <= right) {
tmp[cur++] = arr[r++];
}
cur = 0;
l = left;
while (l <= right) {
arr[l++] = tmp[cur++];
}
}
5.1.8 cardinality sorting (bucket sorting, count sorting)
public static void radixSort(int[] arr) {
int max = arr[0];
for (int i : arr) {
max = max < i ? i : max;
}
int maxLen = ("" + max).length();
int[][] bucket = new int[10][maxLen];
int[] bucketElementCounts = new int[10];
int weishu = 1;// A hundred thousand...
for (int i = 0; i < maxLen; i++, weishu *= 10) {
for (int j = 0; j < arr.length; j++) {
int digit = arr[j] / weishu % 10;
bucket[digit][bucketElementCounts[digit]] = arr[j];
bucketElementCounts[digit]++;
}
int index = 0;
for (int k = 0; k < bucketElementCounts.length; k++) {
if (bucketElementCounts[k] != 0) {
for (int l = 0; l < bucketElementCounts[k]; l++) {
arr[index++] = bucket[k][l];
}
}
bucketElementCounts[k] = 0;
}
}
}
5.2 four common search algorithms
The three commonly used algorithms are: linear search (not simple), binary search and interpolation search
5.2.2 binary search
//Regardless of the target value, if there are more than one, which one should be selected
public static int binarySearch(int[] arr,int from,int to,int target) {
int lo=from,hi=to;
while(lo<=hi) {
int mid=(lo+hi)>>>1;
int midVal=arr[mid];
if(midVal<target) {
lo=mid+1;
}else if(midVal>target) {
hi=mid-1;
}else {
return mid;
}
}
return -1;
}
5.2.3 interpolation search
Its principle is similar to binary search, but it can be self applicable to search from mid
public static int binarySearch(int[] arr, int from, int to, int target) {
int lo = from, hi = to;
while (lo <= hi) {
int mid = (lo + (hi - lo) * (target - arr[lo]) / (arr[hi] - arr[lo]));// self-adaption
int midVal = arr[mid];
if (midVal < target) {
lo = mid + 1;
} else if (midVal > target) {
hi = mid - 1;
} else {
return mid;
}
}
return -1;
}
Conclusion:
Java has been learned for nearly two years. At present, it can understand some underlying source code, but some still can't understand (or have no patience to read), such as Stream in the new features of JDK8. Experienced leaders in source code reading can share it with me in the comment area. I'd like to thank you first. Recently, I will continue to read some important source code of JDK and make records. The above content is my personal record of the whole process of reading the source code. If there is anything wrong with the above content, please tell me in the comment area. Thank you!