2 TPE optimization based on HyperOpt
Hyperopt optimizer is one of the most common Bayesian optimizers at present. Hyperopt integrates several optimization algorithms including random search, simulated annealing and TPE (Tree-structured Parzen Estimator Approach). Compared to Bayes_opt, Hyperopt is a more advanced, modern, better maintained optimizer, and is also the most commonly used optimizer to implement TPE methods. In practice, compared with Bayesian optimization based on Gauss process, TPE based on Gauss mixture model achieves better results in most cases with higher efficiency, which is also widely used in the field of AutoML. The principle of TPE algorithm can be consulted in the original paper. Here we will focus on the process of using TPE in Hyperopt to search for hyperparameters.
import hyperopt from hyperopt import hp, fmin, tpe, Trials, partial from hyperopt.early_stop import no_progress_loss print(hyperopt.__version__) #0.2.7
- 1 Define the objective function
When defining the objective function, we need to strictly follow the basic rules of the current optimization library that need to be used. With Bayes_ Like opt, Hyperopt has specific rules that limit how we define it, including:
1. The input of the objective function must be a hyperopt-compliant dictionary, not a sklearn like parameter space dictionary, not a parameter itself, not an element other than data, algorithms, etc. Therefore, when customizing the objective function, we need to use a hyperparametric spatial dictionary as the input to the objective function.
2. Hyperopt only supports finding the minimum and not the maximum, so when we define an objective function that is a positive indicator (such as accuracy, auc), we need to negatively evaluate that indicator. If the objective function we define is negative loss, we also need to take an absolute value for negative loss. We do not need to change the output if and only if the objective function we define is a general loss.
def hyperopt_objective(params):
#Define an evaluator
#Parameters to search need to be indexed from the input dictionary
#A parameter that does not require a search and can be a set value
#Adjust the parameter type before requiring an integer parameter
reg = RFR(n_estimators = int(params["n_estimators"])
,max_depth = int(params["max_depth"])
,max_features = int(params["max_features"])
,min_impurity_decrease = params["min_impurity_decrease"]
,random_state=1412
,verbose=False
,n_jobs=-1)
#Cross-validation results, output negative root mean square error (-RMSE)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
validation_loss = cross_validate(reg,X,y
,scoring="neg_root_mean_squared_error"
,cv=cv
,verbose=False
,n_jobs=-1
,error_score='raise'
)
#The final output must be absolute (-RMSE) since only the minimum is possible
#To solve the parameter combination corresponding to the minimum RMSE
return np.mean(abs(validation_loss["test_score"]))- 2 Define the parameter space
In any superparametric optimizer, the optimizer takes the combination of superparameters in the parameter space as an alternative combination, and a set of inputs is trained in the algorithm. In Bayesian optimization, the combination of hyperparameters is input into the objective function we defined.
In hyperopt, we use a special dictionary to define the parameter space, where the keys of key-value pairs can be set arbitrarily. As long as they are consistent with the keys of index parameters in the target function, the values of key-value pairs are unique hp functions of hyperopt, including:
Hp. Quniform (parameter name, lower bound, upper bound, step) - for uniformly distributed floating point numbers
Hp. Uniform (parameter name, lower bound, upper bound) - floating point numbers suitable for random distribution
Hp. RandInt (parameter name, upper bound) - an integer for [0, upper bound], with intervals open and closed
hp.choice("parameter name", ["string 1", "string 2",...]) - For string types, optimal parameters are represented by indexes
hp.choice("parameter name", [*range (lower bound, upper bound, step)]) - For integer types, the optimal parameter is represented by an index
hp.choice("parameter name", [integer 1, integer 2, integer 3,...]) - For integer types, optimal parameters are represented by indexes
hp.choice("parameter name", ["string 1", integer 1,...]) - Suitable for mixing characters with integers, with optimal parameters represented by indexes
In the description of hyperopt, it is not clear whether the parameter range space is open or closed. According to the experiment, if there is no special explanation, the parameter space definition methods in hp should be both open intervals before and after closing. We still use the parameter space of the random search that gets the highest score on the random forest:
param_grid_simple = {'n_estimators': hp.quniform("n_estimators",80,100,1)
, 'max_depth': hp.quniform("max_depth",10,25,1)
, "max_features": hp.quniform("max_features",10,20,1)
, "min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,1)
}Because of hp.choice eventually returns the index of the optimal parameter, which can be confused with the specific value of a numeric parameter, whereas hp.randint can only support counting from zero, so we often use quniform to obtain uniformly distributed floating-point numbers instead of integers. For parameter values that require integers, if the parameter space is constructed using quniform, the input type needs to be qualified using the int function in the target function. For example, when taking a value in the range [0,5], you can take [0.0, 1.0, 2.0, 3.0,...] This uniform floating point number, when entering the objective function, must ensure that there is an int function before the parameter value. Of course, if you use hp.choice does not have this problem.
Since continuous variables are not involved, we can calculate the size of the current parameter space:
len([*range(80,100,1)])*len([*range(10,25,1)])*len([*range(10,20,1)])*len([range(0,5,1)]) #3000
- 3 Define the specific process of optimizing the objective function
With the objective function and parameter space, we can then optimize. In Hyperopt, the basic function we use for optimization is called fmin, in fmin, we can customize the proxy model (parameter algo) we use, generally we have tpe.suggest and rand. There are two options for suggest, the former refers to the TPE method and the latter refers to the random grid search method. The partial function can also be used to modify the specific parameters involved in the algorithm, including how many initial observations (parameter n_start_jobs) are used in the model and how many samples (parameter n_EI_candidates) are considered when calculating the values of the collection function. Of course, we can also use the default parameter values without filling in these parameters.
In addition, Hyperopt has two notable features, one that records trials throughout the iteration and the other that stops the parameter early_ahead Stop_ Fn. Trials is translated literally as "experiment" or "test", which means each combination of parameters we keep trying. In this parameter, we usually enter the method Trials(), which is imported from the hyperopt library. When the optimization is completed, we can view the loss, parameters and other intermediate information from the saved trials. And stop parameter early_ahead of time Stop_ In FN we typically enter the method no_imported from the hyperopt Library Progress_ Loss(), in which a specific number n can be entered to indicate that the algorithm stops early when the loss does not decrease for N consecutive times. Due to the high randomness of the Bayesian method, when the sample size is insufficient, multiple iterations are needed to find the optimal solution, so no_ Progress_ The value in loss () is not set too high. In our lesson, due to the small amount of data, I set a higher value to avoid stopping iterations too early.
def param_hyperopt(max_evals=100):
#Save Iteration Process
trials = Trials()
#Setup Stop Early
early_stop_fn = no_progress_loss(100)
#Define the proxy model
#algo = partial(tpe.suggest, n_startup_jobs=20, n_EI_candidates=50)
params_best = fmin(hyperopt_objective #objective function
, space = param_grid_simple #parameter space
, algo = tpe.suggest #Which do you want for the proxy model?#suggest defaults to how many initial observations are used and how many samples are considered when calculating the value of the collection function
#, algo = algo
, max_evals = max_evals #Number of iterations allowed (including initial observations)
, verbose=True
, trials = trials
, early_stop_fn = early_stop_fn
)
#Print the best parameters, fmin will automatically print the best score
print("\n","\n","best params: ", params_best,
"\n")
return params_best, trials4 Define validation functions (unnecessary)
def hyperopt_validation(params):
reg = RFR(n_estimators = int(params["n_estimators"])
,max_depth = int(params["max_depth"])
,max_features = int(params["max_features"])
,min_impurity_decrease = params["min_impurity_decrease"]
,random_state=1412
,verbose=False
,n_jobs=-1
)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
validation_loss = cross_validate(reg,X,y
,scoring="neg_root_mean_squared_error"
,cv=cv
,verbose=False
,n_jobs=-1
)
return np.mean(abs(validation_loss["test_score"]))- 5 Execute actual optimization process
params_best, trials = param_hyperopt(30) #1% space size

params_best, trials = param_hyperopt(100) #3% space size

params_best, trials = param_hyperopt(300) #10% space size

hyperopt_validation(params_best)
#28346.672687223065
#Print all search related records
trials.trials[0]
# {'state': 2,
# 'tid': 0,
# 'spec': None,
# 'result': {'loss': 28766.452192638408, 'status': 'ok'},
# 'misc': {'tid': 0,
# 'cmd': ('domain_attachment', 'FMinIter_Domain'),
# 'workdir': None,
# 'idxs': {'max_depth': [0],
# 'max_features': [0],
# 'min_impurity_decrease': [0],
# 'n_estimators': [0]},
# 'vals': {'max_depth': [13.0],
# 'max_features': [18.0],
# 'min_impurity_decrease': [4.0],
# 'n_estimators': [80.0]}},
# 'exp_key': None,
# 'owner': None,
# 'version': 0,
# 'book_time': datetime.datetime(2021, 12, 24, 13, 33, 19, 633000),
# 'refresh_time': datetime.datetime(2021, 12, 24, 13, 33, 19, 840000)}
#Print the target function values for all searches
trials.losses()[:10]
#[28766.452192638408,
# 29762.22885008687,
# 29233.57333898302,
# 29257.33343872428,
# 29180.63733732971,
# 29249.676793746046,
# 29309.41793204717,
# 28915.33638544984,
# 29122.269575607537,
# 29150.39720576636]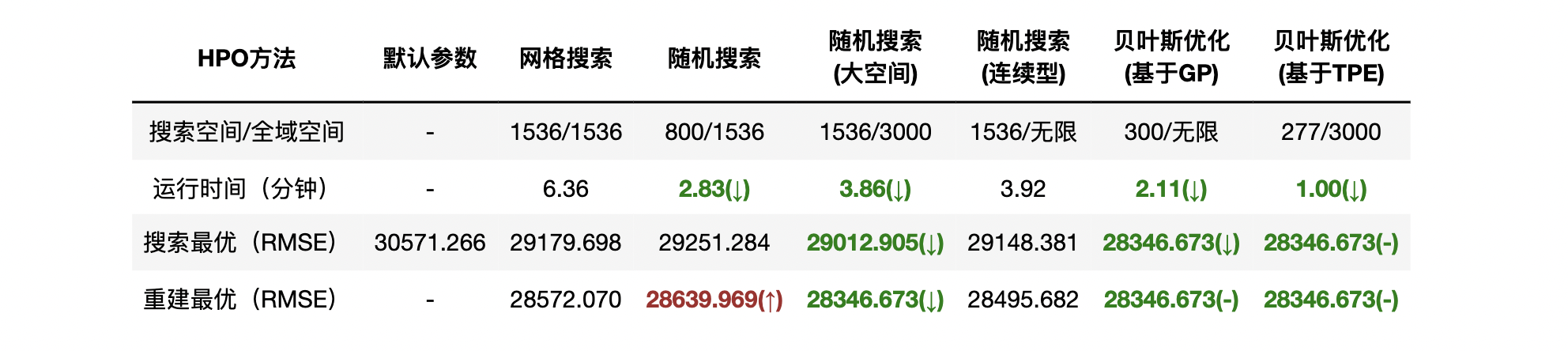
Because of the early stop feature, TPE-based hyperopt optimization may stop before the number of iterations we set is reached, and therefore the number of iterations required for hyperopt to iterate to the actual optimal value may be less. At the same time, the TPE method is faster than the Gaussian process calculation, so in 277 iterations, hyperopt only takes 1 minute, while bayes_runs 300 iterations Opti takes 2.11 minutes, so hyperopt is more advantageous even if you run the same number of iterations, perhaps because the parameter space of hyperopt is more sparse and integer parameter searches are more efficient.
However, the disadvantage of HyperOpt is that it requires high precision and flexibility, and slight changes can make it difficult to run code with crazy errors. At the same time, there are not enough optimization algorithms supported by HyperOpt. If we focus on using TPE methods, we can master HyperOpt, and if we want to have a rich HPO means, we can have a deeper access to the Optuna library.
3 Multiple Bayesian optimizations based on Optuna
Optuna is by far the most mature and extensible superparametric optimization framework, compared with the old bayes_ Optuna is obviously designed for machine learning and in-depth learning, compared with opt. To meet the needs of machine learning developers, Optuna has a powerful and fixed API, so Optuna code is simple and highly modular, which is the most concise Library in the library we've introduced. The advantage of Optuna is that it can be seamlessly connected to deep learning frameworks such as PyTorch and Tensorflow, or used in conjunction with scikit-optimize, Sklearns optimization library, so Optuna can be used in a variety of optimization scenarios. In our course, we will focus on Optuna's Bayesian optimization process. Other optimization aspects can be found on the following pages: GitHub - optuna/optuna: A hyperparameter optimization framework .
import optuna print(optuna.__version__) #2.10.0
- 1 Define objective function and parameter space
Optuna's target function is quite special. In other optimization libraries, we need to input parameter or parameter space separately. The optimizer will put parameter space into our objective function to optimize one by one in the specific optimization process. However, in Optuna, we do not need to input parameter or parameter space into the objective function, but need to define parameter space directly in the objective function. In particular, the Optuna optimizer generates a trial (a set of parameter combinations entered into our objective function) which refers to an alternative parameter that cannot be obtained or opened by the user, but that variable exists in the optimizer and is entered into the objective function. In the objective function, we can construct a parameter space by the method carried by the variable trail, as follows:
def optuna_objective(trial):
#Define parameter space
n_estimators = trial.suggest_int("n_estimators",80,100,1) #Integer type (parameter name, lower bound, upper bound, step)
max_depth = trial.suggest_int("max_depth",10,25,1)
max_features = trial.suggest_int("max_features",10,20,1)
#max_features = trial.suggest_categorical("max_features",["log2","sqrt","auto"]) #Character
min_impurity_decrease = trial.suggest_int("min_impurity_decrease",0,5,1)
#min_impurity_decrease = trial.suggest_float("min_impurity_decrease",0,5,log=False) #float
#Define an evaluator
#The parameters that need to be optimized are determined by the above parameter space
#Fill in the values directly without optimizing the parameters
reg = RFR(n_estimators = n_estimators
,max_depth = max_depth
,max_features = max_features
,min_impurity_decrease = min_impurity_decrease
,random_state=1412
,verbose=False
,n_jobs=-1
)
#Cross-validation process, outputting negative root mean square error (-RMSE)
#optuna supports both maximization and minimization, so if output-RMSE, choose maximization
#If Output RMSE is selected, then Minimize
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
validation_loss = cross_validate(reg,X,y
,scoring="neg_root_mean_squared_error"
,cv=cv #Cross-validation mode
,verbose=False #Whether to print the process
,n_jobs=-1 #Number of threads
,error_score='raise'
)
#Final Output RMSE
return np.mean(abs(validation_loss["test_score"]))- 2 Define the flow of optimizing the objective function
In HyperOpt, we can adjust the algo parameter to customize the specific algorithm used to perform Bayesian optimization, or in Optuna. Most of the alternative algorithms are focused on Optuna's module sampler, including TPE optimization, random grid search, and other more advanced Bayesian processes that we are familiar with, for Optuna. Classes called out in sampler can also be entered directly to set the number of initial observations and the amount of observations to be considered each time the collection function is calculated. There is no integrated way to implement the Gaussian process in the Optuna library, but we can import the Gaussian process from scikit-optimize as an algo setting in optuna. Specific parameters related to the Gaussian process can be set as follows:
def optimizer_optuna(n_trials, algo):
#Define using TPE or GP
if algo == "TPE":
algo = optuna.samplers.TPESampler(n_startup_trials = 10, n_ei_candidates = 24)#The default starts with 10 observations, and 24 sets of parameter combinations are randomly selected for each calculation of the collection function
elif algo == "GP":
from optuna.integration import SkoptSampler #skilearn-optimize
import skopt
algo = SkoptSampler(skopt_kwargs={'base_estimator':'GP', #Selecting a Gaussian Process
'n_initial_points':10, #10 initial observation points
'acq_func':'EI'} #Selected collection function is EI, expected increment
)
#Actual optimization process, first instantiate the optimizer
study = optuna.create_study(sampler = algo #Sampling samples using the specific algorithm sampler
, direction="minimize" #Optimized direction, minimize or maximize can be filled in
)
#Begin optimization, n_trials is the maximum number of iterations allowed
#Since the parameter space is already defined in the target function, no input parameter space is required
study.optimize(optuna_objective #objective function
, n_trials=n_trials #Maximum number of iterations (including initial observations)
, show_progress_bar=True #Would you like to show the progress bar?
)
#Optimized results can be invoked directly from the optimized object study
#Print Optimal Parameters and Optimal Loss Value
print("\n","\n","best params: ", study.best_trial.params,
"\n","\n","best score: ", study.best_trial.values,
"\n")
return study.best_trial.params, study.best_trial.values- 3 Perform actual optimization process
Although the Optuna library is one of the most mature HPO methods today, when the parameter space is small, the Optuna library is prone to sample BUG in iteration, that is, Optuna will continue to pull to the parameter combinations that have been pumped before, and keep alerting that "the algorithm has checked the target function on this parameter combinations". In the actual iteration, once this bug appears, the current iteration is useless, because the observed values that have been tested will not help with optimization, so optimization for loss will stop. If this BUG appears, you can increase the range or density of the parameter space. Or use the following code to turn off the warning:
import warnings
warnings.filterwarnings('ignore', message='The objective has been evaluated at this point before.')
best_params, best_score = optimizer_optuna(10,"GP") #Default print iteration process
# 0%| | 0/10 [00:00<?, ?it/s]
# [I 2021-12-24 22:14:28,229] Trial 0 finished with value: 28848.70339210933 and parameters: {'n_estimators': 99, 'max_depth': 14, 'max_features': 16, 'min_impurity_decrease': 4}. Best is trial 0 with value: 28848.70339210933.
# [I 2021-12-24 22:14:29,309] Trial 1 finished with value: 28632.395126147465 and parameters: {'n_estimators': 90, 'max_depth': 23, 'max_features': 16, 'min_impurity_decrease': 2}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:30,346] Trial 2 finished with value: 29301.159287113685 and parameters: {'n_estimators': 89, 'max_depth': 17, 'max_features': 12, 'min_impurity_decrease': 0}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:31,215] Trial 3 finished with value: 29756.446415640086 and parameters: {'n_estimators': 80, 'max_depth': 11, 'max_features': 14, 'min_impurity_decrease': 3}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:31,439] Trial 4 finished with value: 29784.547574554617 and parameters: {'n_estimators': 88, 'max_depth': 11, 'max_features': 15, 'min_impurity_decrease': 2}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:31,651] Trial 5 finished with value: 28854.291800282757 and parameters: {'n_estimators': 82, 'max_depth': 12, 'max_features': 18, 'min_impurity_decrease': 3}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:31,853] Trial 6 finished with value: 29268.28890743908 and parameters: {'n_estimators': 80, 'max_depth': 10, 'max_features': 19, 'min_impurity_decrease': 5}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:32,111] Trial 7 finished with value: 29302.5258321895 and parameters: {'n_estimators': 99, 'max_depth': 16, 'max_features': 14, 'min_impurity_decrease': 3}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:32,353] Trial 8 finished with value: 29449.903990989755 and parameters: {'n_estimators': 80, 'max_depth': 21, 'max_features': 17, 'min_impurity_decrease': 1}. Best is trial 1 with value: 28632.395126147465.
# [I 2021-12-24 22:14:32,737] Trial 9 finished with value: 29168.76064401323 and parameters: {'n_estimators': 97, 'max_depth': 22, 'max_features': 17, 'min_impurity_decrease': 1}. Best is trial 1 with value: 28632.395126147465.
# best params: {'n_estimators': 90, 'max_depth': 23, 'max_features': 16, 'min_impurity_decrease': 2}
# best score: [28632.395126147465]
optuna.logging.set_verbosity(optuna.logging.ERROR) #Turn off auto-printed info and show progress bar only
#optuna.logging.set_verbosity(optuna.logging.INFO)
best_params, best_score = optimizer_optuna(300,"TPE")
# 0%| | 0/300 [00:00<?, ?it/s]
# best params: {'n_estimators': 96, 'max_depth': 22, 'max_features': 14, 'min_impurity_decrease': 3}
# best score: [28457.22400533479]
optuna.logging.set_verbosity(optuna.logging.ERROR)
best_params, best_score = optimizer_optuna(300,"GP")
# 0%| | 0/300 [00:00<?, ?it/s]
# best params: {'n_estimators': 87, 'max_depth': 23, 'max_features': 16, 'min_impurity_decrease': 5}
# best score: [28541.05837443567] Obviously, Bayesian optimization based on Gaussian process runs slower than TPE-based Bayesian optimization. When Optuna was debugging, I didn't run it many times and pulled out the best value of Optuna, so we can skip comparing the results of Optuna to tables, but in TPE mode, it runs at a speed very close to that of HyperOpt. In future lessons, unless otherwise specified, we will use the TPE method by default to optimize.