catalogue
1. Dichotomy search
Dichotomy search (half search):
First: dichotomy search is based on sorting.
Second: the efficiency of binary search is higher than that of "one by one".
Third: dichotomy search principle?
10 (0 subscript) 23 56 89 100 111 222 235 500 600 (subscript 9) arr array
Objective: find the subscript of 600
(0 + 9) / 2 -- > 4 (subscript of intermediate element)
The element arr[4] is the intermediate element: arr[4] is 100
100 < 600
Indicates that the element to be found is on the right of 100.
Then the subscript becomes: 4 + 1
(5 + 9) / 2 -- > 7 (subscript of intermediate element)
arr[7] corresponds to: 235
235 < 600
Indicates that the element to be searched is on the right of 235.
At the beginning, the subscript has changed again: 7 + 1
(8 + 9) / 2 --> 8
arr[8] --> 500
500 < 600
The subscript of the start element has changed again: 8 + 1
(9 + 9) / 2 --> 9
arr[9] is 600, which is exactly equal to 600. At this time, it is found.
/**
* @company: Beijing power node
* @author:Korean National Day
*/
public class BinarySearch {
public static void main(String[] args) {
int[] array = new int[]{10,11,12,13,14,15,16,17};
int target = 10;
int index = search(array, target);
System.out.println(index);
}
public static int search(int[] array,int target){
//Minimum index pointer
int min = 0;
int max = array.length-1;
while (min<=max){
//Calculate the average index position
int mid = (min+max)/2;
if (array[mid]== target){
return mid;
}
if (array[mid]<target){
min = mid+1;
}
if (array[mid]>target){
max = mid-1;
}
}
return -1;
}
}2. Interpolation search

Array arr = [1, 2, 3,..., 100]
Suppose we need to find the value 1
Using binary search, we need to recurse many times to find 1
Using interpolation lookup algorithm
int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])
int mid = 0 + (99 - 0) * (1 - 1)/ (100 - 1) = 0 + 99 * 0 / 99 = 0
For example, the value we find is 100
int mid = 0 + (99 - 0) * (100 - 1) / (100 - 1) = 0 + 99 * 99 / 99 = 0 + 99 = 99
package com.bjpowernode.select;
/**
* @company: Beijing power node
* @author:Korean National Day
*/
public class InsertSelect {
public static void main(String[] args) {
int[] array = {1,2,3,4,5,6};
int left = 0;
int right = array.length-1;
int searchVal = 1;
System.out.println(select(array,left,right,searchVal));
}
public static int select(int[] array,int left,int right,int searchVal){
/**
* Prevent array out of bounds
*/
if (left>right || searchVal<array[0] || searchVal>array[array.length-1]){
return -1;
}
int mid = left+(right-left)*(searchVal-array[left])/(array[right]-array[left]);
int midValue = array[mid];
if (searchVal>midValue){
return select(array,mid+1,right,searchVal);
}else if (searchVal<midValue){
return select(array,left,mid-1,searchVal);
}else {
return mid;
}
}
}
3 Fibonacci search
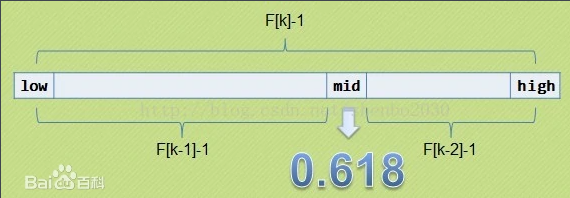
Fibonacci is no longer in the middle, but near the golden section, that is, mid=low+F(k-1)-1
From the properties of Fibonacci sequence F[k]=F(k-1)+F(k-2), we can get (F[k]-1) = (F(k-1) -1) +(F[k-2]-1) +1
Understanding of F(k-1)-1:
1) As long as the length of the sequence table is F[k]-1, the table can be divided into two sections with the length of F[k-1]-1 and F[k-2]-1, so that the middle position is mid=low+F(k-1)-1.
2) Similarly, each field can be split in the same way
3) However, the length n of the sequence table is not necessarily equal to f [k] - 1, so the length n of the original sequence table needs to be increased to f [k] - 1. As long as the K value here can make f [k] - 1 exactly greater than or equal to N, it can be obtained from the following code. After the length of the sequence table increases, the new positions (from n+1 to f [k] - 1) are all n-trusted values.
package com.bjpowernode.select;
import java.util.Arrays;
/**
* @company: Beijing power node
* @author:Korean National Day
*/
public class FibonacciSelect {
public static void main(String[] args) {
int[] array = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
System.out.println(select(array,13));
}
/**
* f[k] = (f[k-1])+ (f[k-2])
* @return
*/
public static int[] f(){
int[] f = new int[20];
f[0] = 1;
f[1] = 1;
for (int i = 2;i<f.length;i++){
f[i] = f[i-1]+f[i-2];
}
return f;
}
/**
* mid = low+F(k-1)-1
* @param array
* @param key
* @return
*/
public static int select(int[] array,int key){
int low = 0;
int hight = array.length-1;
int k = 0;
int mid = 0;
int[] f = f();
/**
* Find split point
*/
while (hight>f[k]-1){
k++;
}
int[] temp = Arrays.copyOf(array,f[k]);
/**
* {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89} -=>{1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,89,89,}
*/
for (int i = hight+1;i<temp.length;i++){
temp[i] = array[hight];
}
while (low<=hight){
mid = low+f[k-1]-1;
// f[k-1]+f[k-2] = f[k];
if (key<temp[mid]){
hight=mid-1;
k--;
}else if (key>temp[mid]){
low = mid+1;
k-=2;
}else{
if (mid<=hight){
return mid;
}else {
return hight;
}
}
}
return -1;
}
}