1, Linear search algorithm
Linear search algorithm, that is, compare one by one according to the order of the array until the target value is found.
For example, there is a sequence: {1,8, 10, 89, 1000, 1234}. Judge whether the sequence contains this name. Requirements: if it is found, prompt to find it and give the following benchmark value:
/**
* Linear search
*/
public class SeqSearch {
public static void main(String[] args) {
int [] arr={1,8,0,2,5};
int index=seqSearch(arr,5);
if(index == -1){
System.out.println("can't find");
}else {
System.out.println("In the first"+index+"position");
}
}
/**
* Find one and return the result
* @param arr
* @param value Value to find
* @return
*/
private static int seqSearch(int[] arr, int value) {
for (int i = 0; i < arr.length; i++) {
if(arr[i]==value){
return i;
}
}
return -1;
}
}
2, Binary search algorithm
Example: Please binary search {1,8, 10, 89, 1000, 1234} for an ordered array, enter a number to see if this number exists in the array, and find the subscript. If not, you will be prompted with "no this number".
Idea:
2.1 recursive method
/**
* Binary search, on the premise that the array is ordered
*/
public class BinarySearch {
public static void main(String[] args) {
int [] arr={1,8,0,2,5};
int index=binarySearch01(arr,0,arr.length-1,5);
if(index == -1){
System.out.println("can't find");
}else {
System.out.println("In the first"+index+"position");
}
}
//Recursive method
private static int binarySearch01(int[] arr, int left, int right,int value) {
if(left>right){
return -1;
}
int mid=(left+right)/2;
if(arr[mid]==value){
return mid;
}else if(arr[mid]<value){
return binarySearch01(arr,mid+1,right,value);
}else{
return binarySearch01(arr,left,mid,value);
}
}
}
2.2 non recursive method
//Non recursive implementation of binary search
/**
*
* @param arr The array to be searched, arr is sorted in ascending order
* @param target Number of to find
* @return Return the corresponding subscript, - 1 means it is not found
*/
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while(left <= right) { //Description continue to find
int mid = (left + right) / 2;
if(arr[mid] == target) {
return mid;
} else if ( arr[mid] > target) {
right = mid - 1;//You need to look to the left
} else {
left = mid + 1; //You need to look to the right
}
}
return -1;
}
2.3 expansion
After class thinking questions: {1,8, 10, 89, 1000, 10001234} when there are multiple identical values in an ordered array, how to find all the values, such as 1000 here
Idea:
- Do not return the mid index value immediately after it is found
- Scan to the left of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
- Scan to the right of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
- Set Arraylist
public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {
// When left > right, it means that the whole array is recursive, but it is not found
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // Recursive right
return binarySearch2(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // Left recursion
return binarySearch2(arr, left, mid - 1, findVal);
} else {
// *Train of thought analysis
// * 1. Do not return the mid index value immediately after it is found
// * 2. Scan to the left of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
// * 3. Scan to the right of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
// * 4. Return Arraylist to
List<Integer> resIndexlist = new ArrayList<Integer>();
//Scan to the left of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
int temp = mid - 1;
while (true) {
if (temp < 0 || arr[temp] != findVal) {//sign out
break;
}
//Otherwise, put temp into reindexlist
resIndexlist.add(temp);
temp -= 1; //temp shift left
}
resIndexlist.add(mid); //
//Scan to the right of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
temp = mid + 1;
while (true) {
if (temp > arr.length - 1 || arr[temp] != findVal) {//sign out
break;
}
//Otherwise, put temp into reindexlist
resIndexlist.add(temp);
temp += 1; //temp shift right
}
return resIndexlist;
}
}
3, Interpolation search algorithm
- Introduction to interpolation search principle:
The interpolation search algorithm is similar to binary search, except that the interpolation search starts from the adaptive mid each time. - The mid index formula in the split search is used. low represents the left index, high represents the right index, and right Key is the findVal we talked about earlier

- int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]) ;/ Interpolation index/
Corresponding to the previous code formula:
int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])

/**
* Interpolation search algorithm, premise [ordered] sequence
*/
public class InsertValSearch {
public static void main(String[] args) {
// int [] arr = new int[100];
// for(int i = 0; i < 100; i++) {
// arr[i] = i + 1;
// }
int arr[] = { 1, 8, 10, 89,1000,1000, 1234 };
int index = insertValueSearch(arr, 0, arr.length - 1, 1234);
//int index = binarySearch(arr, 0, arr.length, 1);
System.out.println("index = " + index);
//System.out.println(Arrays.toString(arr));
}
//Write interpolation search algorithm
//Interpolation search algorithm also requires that the array is ordered
/**
*
* @param arr array
* @param left Left index
* @param right Right index
* @param findVal Find value
* @return If it is found, the corresponding subscript is returned. If it is not found, it returns - 1
*/
public static int insertValueSearch(int[] arr, int left, int right, int findVal) {
System.out.println("Interpolation lookup times~~");
//Note: findval < arr [0] and findval > arr [arr.length - 1] must be required
//Otherwise, the mid we get may cross the border
if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {
return -1;
}
// Find the mid, adaptive
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midVal = arr[mid];
if (findVal > midVal) { // Description should recurse to the right
return insertValueSearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // Description left recursive lookup
return insertValueSearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
}
Precautions for interpolation search:
- For the lookup table with large amount of data and uniform keyword distribution, interpolation search is faster
- In the case of uneven keyword distribution, this method is not necessarily better than half search
4, Fibonacci (golden section) search algorithm
- Golden section point refers to dividing a line segment into two parts, so that the ratio of one part to the total length is equal to the ratio of the other part to this part. The approximate value of the first three digits is 0.618. Because the shape designed according to this proportion is very beautiful, it is called the golden section, also known as the Chinese foreign ratio. This is a magical number, which will bring little intention.
- Fibonacci sequence {1, 1, 2, 3, 5, 8, 13, 21, 34, 55} it is found that the ratio of two adjacent numbers of Fibonacci sequence is infinitely close to the golden section value of 0.618
4.1 principle
The Fibonacci search principle is similar to the first two, only changing the position of the middle knot (MID). The mid is no longer obtained by middle or interpolation, but located near the golden section point, that is, mid=low+F(k-1)-1 (f represents Fibonacci sequence), as shown in the figure below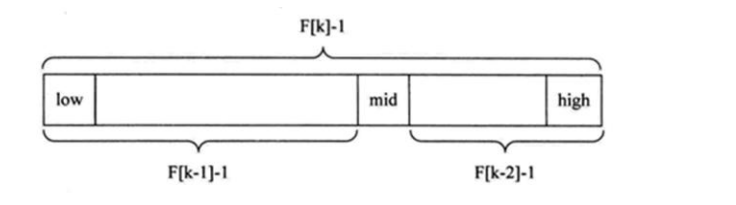
Understanding of F(k-1)-1:
- From the property of Fibonacci sequence F[k]=F[k-1]+F[k-2], we can get (F[k]-1) = (F[k-1]-1) + (F[k-2]-1) + 1. The formula shows that as long as the length of the sequence table is F[k]-1, the table can be divided into two segments with the length of F[k-1]-1 and F[k-2]-1, as shown in the above figure. Therefore, the middle position is mid=low+F(k-1)-1
- Similarly, each sub segment can be divided in the same way
- However, the length n of the sequence table is not necessarily equal to F[k]-1, so the length n of the original sequence table needs to be increased to F[k]-1. As long as the K value here can make F[k]-1 exactly greater than or equal to N, it can be obtained from the following code. After the length of the sequence table increases, the new positions (from n+1 to F[k]-1) can be assigned as the value of n position.
while(n>fib(k)-1)
k++;
4.2 code implementation
Please perform Fibonacci search on an ordered array {1,8, 10, 89, 1000, 1234}, enter a number to see if this number exists in the array, and find the subscript. If not, you will be prompted with "no such number".
/**
* The premise of Fibonacci search algorithm requires that the sequence is [ordered sequence]
*/
public class FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int [] arr = {1,8, 10, 89, 1000, 1234};
System.out.println("index=" + fibSearch(arr, 189));// 0
}
//Because we need Fibonacci sequence for Mid=low+f(k-1)-1
//A Fibonacci sequence is obtained by non recursive method
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 0;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
//Write Fibonacci search algorithm
//Write the algorithm in a non recursive way
/**
* @param a array
* @param key Key (value) we need to find
* @return Returns the corresponding subscript, if not - 1
*/
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0; //Subscript representing the Fibonacci division value
int mid = 0; //Store mid value
int f[] = fib(); //Get Fibonacci sequence
//Get the subscript of Fibonacci division value
while (high > f[k] - 1) {
k++;
}
//Because the f[k] value may be greater than the length of a, we need to use the Arrays class to construct a new array and point to temp []
//The insufficient part will be filled with 0
int[] temp = Arrays.copyOf(a, f[k]);
//In fact, you need to fill temp with the last number of the a array
//give an example:
//temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 1234,}
for (int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
// Use while to cycle and find our number key
while (low <= high) { // As long as this condition is met, you can find it
mid = low + f[k - 1] - 1;
if (key < temp[mid]) { //We should continue to look in front of the array (left)
high = mid - 1;
//Why k--
//explain
//1. All elements = front elements + rear elements
//2. f[k] = f[k-1] + f[k-2]
//Because there are f[k-1] elements in front, you can continue to split f[k-1] = f[k-2]+f[k-3]
//That is, continue to find K in front of f[k-1]--
//That is, the next cycle mid = f[k-1-1]-1
k--;
} else if (key > temp[mid]) { // We should continue to look behind the array (to the right)
low = mid + 1;
//Why k -=2
//explain
//1. All elements = front elements + rear elements
//2. f[k] = f[k-1] + f[k-2]
//3. Since we have f[k-2], we can continue to split f[k-1] = f[k-3] + f[k-4]
//4. Find k -=2 in front of f[k-2]
//5. That is, the next cycle mid = f[k - 1 - 2] - 1
k -= 2;
} else { //find
//You need to determine which subscript is returned
//Note: because there is array filling in the front, mid > high, the following values are the same, and high is returned
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
}