Introduction: when developing middle and background applications or middleware, we will store some data in memory to speed up access. With the increase of the amount of data, in addition to being placed on the heap, it can also be alleviated by real-time compression. Today we will introduce a way to compress and shape arrays.

Author Xuan Yin
Source: Ali technical official account

When developing middle and background applications or middleware, we will store some data in memory to speed up access. With the increase of the amount of data, in addition to being placed on the heap, it can also be alleviated by real-time compression. Today we will introduce a way to compress and shape arrays.

I. data compression

Array refers to long [] or int [] type, which is widely used in Java. When there is a large amount of data, the problem of memory occupation is highlighted. The reason is that a long type occupies 8 bytes, and int also occupies 4 bytes. When there are tens of millions of levels of data, the space occupied is hundreds of MB.

1. De redundancy

The first thought is to reduce the space occupied by each number. Because we all know that in terms of positive numbers, more than 3 bytes of int can mean 2^24 = 16M, that is, 1600 million. Later, when the fourth byte is used, most of us can't use it, but we can't cut it off. In case we still need it; Therefore, it is a feasible idea to remove the high bit, but it must be removed dynamically. It still needs to be used when it should be used, which requires how many bytes to be stored (see Figure: basic principle of digital compression).

Basic principles of digital compression

There are two ways to represent the number of bytes occupied by data: one is to borrow several bits of the original data. Take long for example, we only need to borrow 3 bits to cover the number of bytes used (because 2) ˆ 3 = 8), since 2 ^ 60 is already a very large number and can hardly be used, our borrowing will basically not produce negative effects; The other is to use the highest byte to indicate that there is still remaining data (see Figure 2). Facebook uses this method to compress the transmitted data in Thrift. In short, we want to compress the long or int array into a byte array, and then restore the corresponding numbers according to the information stored in the byte array.

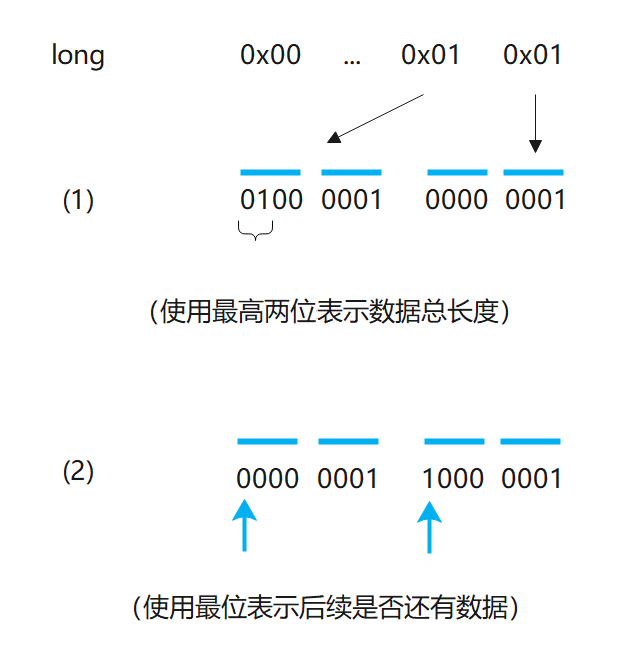
Method for identifying data size during decompression

The above compression ideas can well solve the access problem in the transmission scenario, because they are all forward first out ideas, but what if we need the compressed structure to still have the subscript access ability of the array?

The difficulty here is: before, each number was of fixed length. We can quickly find the corresponding memory address through "[number of bytes occupied by a single number] * [number]", but the space occupied by each number after compression is not the same. This method fails. We can't know the memory location of the nth number. Can we only find the value marked 200 linearly 200 times? Obviously, such efficiency is quite low, and its time complexity decreases from O(1) to O(n). Is there a better way? Of course. We can establish an index (as shown in the figure below), namely:

• Divide the number into several buckets, and the size of the bucket can be adjusted (for example, one bucket of 1KB, one bucket of 4KB, etc.)
• We use another array, the size of which is the number of buckets, to store the subscript of the first data in each bucket
• When searching, I first use bisection to find the corresponding bucket, and then use linear to find the corresponding data

  

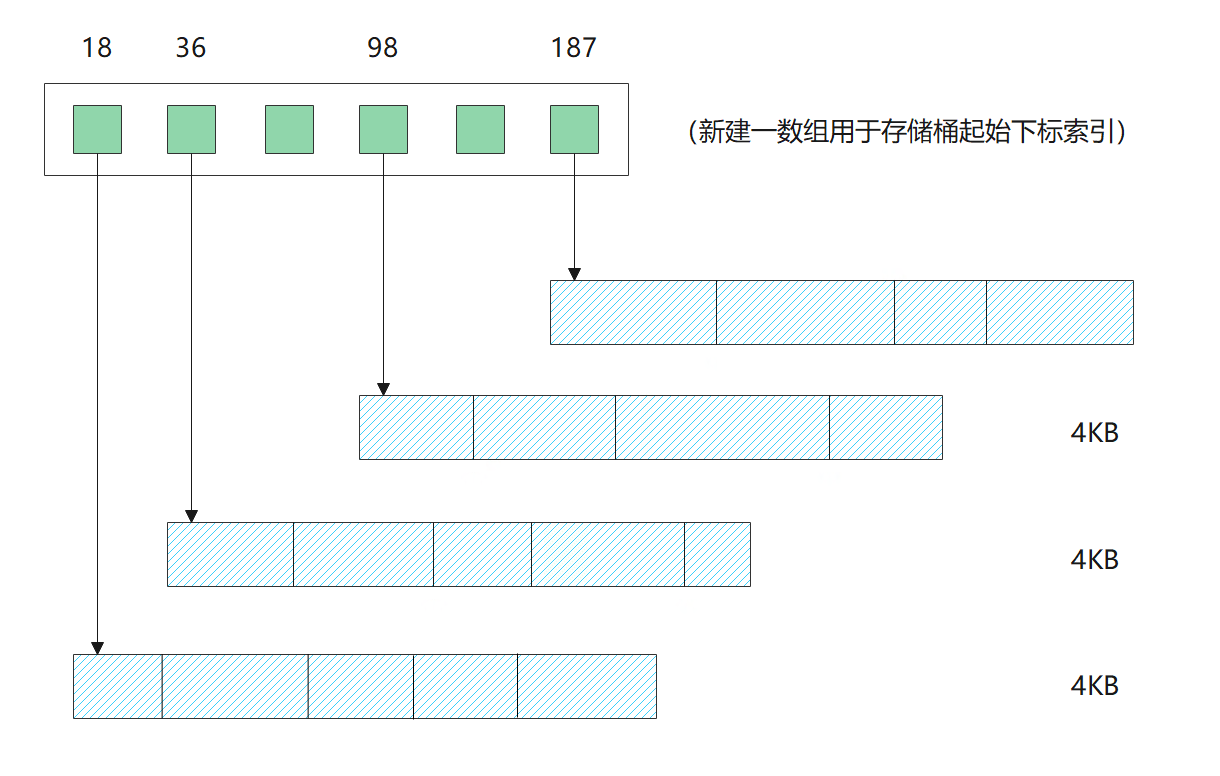
Indexing can improve the speed of subscript acquisition after compression

Because it is only a linear search in the bucket, it is generally not too large, 1KB or 4KB (not too small, because the array pointer of each bucket also needs to occupy 16B). Since the first index binary search solves most problems, the search speed is significantly improved, close to O(logN). Using this method, it has been tested that the occupied space can be reduced by about 30% in the case of 400 million random data. After simple test, TPS can reach 100w level, and single access is certainly enough.

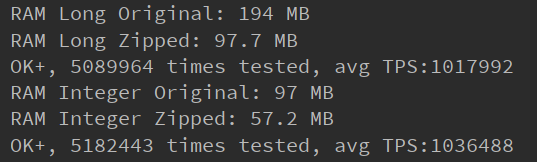
Compression effect

2 offset storage

Using the nature of sequential search in the bucket, we can only store the original number in the first element in the bucket and an offset in the following elements, because when the data is not obviously discrete (that is, it is more than ten or billions at one time), the data size can be well reduced. For example, both numbers occupy 3 bytes. After storing the offset, The second number can be represented by 1 ~ 2 bytes. Of course, if you have no requirements for the order of the array itself, you can sort the array first, and the effect of this offset can be broken. In most cases, it can be reduced by more than 70%.

Second access optimization

During the performance pressure test of an online application of the above scheme, we found that the single random acquisition was not affected, but the batch sequential acquisition interface decreased by as much as 97%, from more than 2800 to 72. Through research, it is found that the reason why the batch interface decreases significantly is that it touches the upper limit of randomly obtained TPS, As shown in the "figure: compression effect", the limit TPS of random acquisition is about 100w, but in the batch sequence scenario, each batch operation will perform 1\~3w retrieval operations. Each retrieval operation uses the random acquisition interface, so it can only be a two digit TPS such as 72. Therefore, we need to deeply optimize the access efficiency of compressed data. To this end, we take the following measures.

1 change fixed length barrel to variable length barrel

Previously, the binary search is a factor. We use fixed length buckets (i.e. the number of bytes stored in each bucket is equal), and the number of numbers stored in each bucket is variable. However, if we use variable length buckets to store N numbers in each bucket, we can quickly hit the bucket where the number is located by "division + remainder", In this way, we can find the bucket subscript with the complexity of O(1), which is much faster than the previous binary O(logn). After testing, the TPS of batch interface is increased by about 320, more than 4 times, and the effect is obvious.

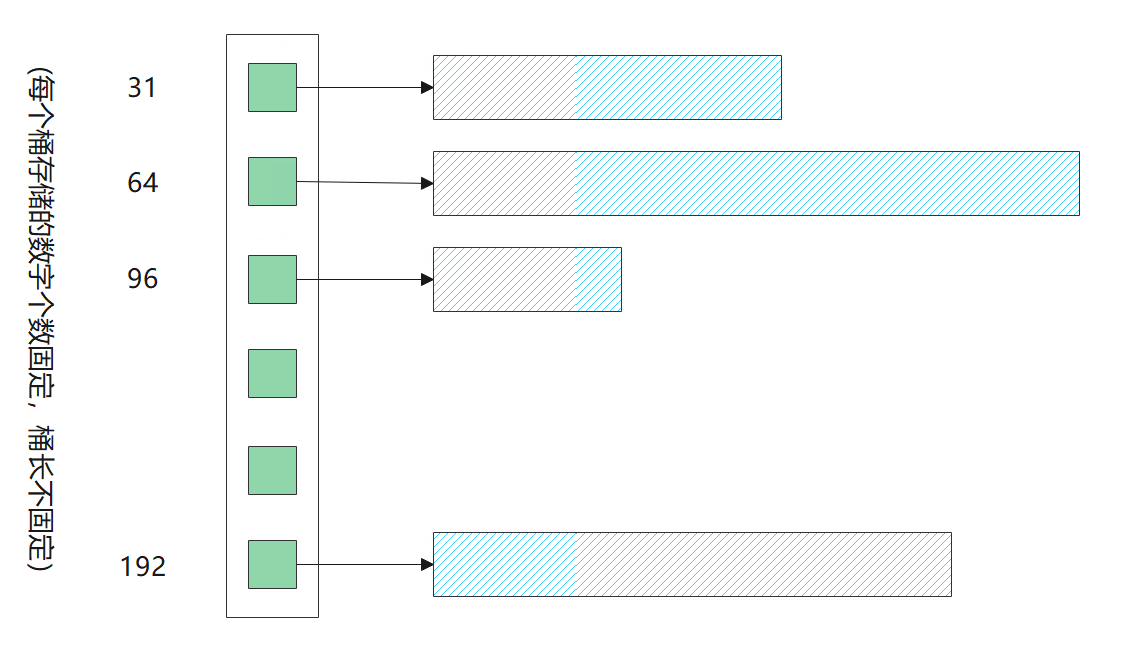
Non fixed bucket length can fix the length of index block, which can be found quickly

2 write a special iterator

In fact, batch is the instance operation. Previously, the instance was taken individually, that is, each time through the get interface. This interface will calculate the position of the bucket every time, then the offset, and then find it one by one from the beginning of the bucket according to the offset. Of course, the performance overhead is large under a large number of requests. Therefore, we can specially design an iterator according to the characteristics of sequential fetching. The first initialization of this iterator will record the position of the bucket. Next time, we can really offset the length n of a number and directly find the next data. Its time complexity is O(1). After testing, the TPS of batch interface can be increased to about 680.

3. Reduce intermediate data and use stack direct transfer for sharing

In the original decompression process, we read the data from the bucket and then pass it to the solution for decompression. Here, a large amount of intermediate data will be generated in the heap, and many ByteBuffer wrap operations will be used before. Wrap will create a ByteBuffer object each time, which is quite time-consuming. Since these are read-only operations and data deletion is not supported at present, we can directly reference the data in the bucket and pass it to the decompression function through the stack, which will be much faster.

The code before modification is as follows, and its main logic is

1. Calculate the bucket and offset of the number, and then wrap it into ByteBuffer
2. Use the packed ByteBuffer to linearly analyze the byte array and find the number in the bucket through the offset
3. Copy the corresponding bytes into a temporary array according to the length information of the number (i.e. the first three bits)
4. Pass the temporary array into the inflate method for decompression

public long get(int ix) {
        // First, find the shard. Since each bucket stores a fixed number of numbers, it can be mapped directly
        int i = ix / SHARD_SIZE;

        // The rest is the offset that needs linear lookup
        ix %= SHARD_SIZE;

        ByteBuffer buf = ByteBuffer.wrap(shards[i]);

        // Find the offset of the corresponding data
        long offset = 0;
        if (ix > 0) {
            int len = (Byte.toUnsignedInt(buf.get(0)) >>> 5);

            byte[] bag = new byte[len];
            buf.get(bag, 0, len);
            offset = inflate(bag);
        }

        // Reset position 
        buf.position(0);

        int numPos = 0;
        while (ix > 0) {
            int len = (Byte.toUnsignedInt(buf.get(numPos)) >>> 5);

            numPos += len;
            ix -= 1;
        }
        buf.position(numPos);

        int len = (Byte.toUnsignedInt(buf.get(numPos)) >>> 5);

        byte[] bag = new byte[len];
        buf.get(bag, 0, len);

        return offset + inflate(bag);
    }
}

private static long inflate(byte[] bag) {
        byte[] num = {0, 0, 0 ,0 ,0 ,0, 0, 0};

        int n = bag.length - 1;
        int i;
        for (i = 7; n >= 0; i--) {
            num[i] = bag[n--];
        }

        int negative = num[i+1] & 0x10;

        num[i + 1] &= 0x0f;
        num[i + 1] |= negative << 63;

        return negative > 0 ? -ByteBuffer.wrap(num).getLong() : ByteBuffer.wrap(num).getLong();
    }
}

Modified code:

public long get(int ix) {
        // First, find the shard. Since each bucket stores a fixed number of numbers, it can be mapped directly
        int i = ix / SHARD_SIZE;

        // The rest is the offset that needs linear lookup
        ix %= SHARD_SIZE;

        byte[] shard = shards[i];

        // Find the offset of the corresponding data
        long offset = 0;
        if (ix > 0) {
            int len = (Byte.toUnsignedInt(shard[0]) >>> 5);
            offset = inflate(shards[i], 0, len);
        }

        int numPos = 0;
        while (ix > 0) {
            int len = (Byte.toUnsignedInt(shard[numPos]) >>> 5);

            numPos += len;
            ix -= 1;
        }

        int len = (Byte.toUnsignedInt(shard[numPos]) >>> 5);

        return offset + inflate(shards[i], numPos, len);
}

private static long inflate(byte[] shard, int numPos, int len) {
        byte[] num = {0, 0, 0 ,0 ,0 ,0, 0, 0};

        System.arraycopy(shard, numPos, num, num.length - len, len);

        int i = num.length - len;
        int negative = num[i] & 0x10;

        num[i] &= 0x0f;
        num[i] |= negative << 63;

        return negative > 0 ? -longFrom8Bytes(num) : longFrom8Bytes(num);
}

It can be seen from the comparison that the intermediate variable bag array is mainly removed here, and the byte array corresponding to the data is directly obtained by referencing the data in the original shard. Before, the byte data in the bucket was obtained through the ByteBuffer. Now we directly find it through shard[i], which is much more efficient. After testing, this optimization can improve the performance by about 45% and directly increase the TPS to more than 910.

4 change heap data to stack data

This transformation point is somewhat difficult. For intermediate variables, some can be avoided. We can use the above methods, but some cannot be avoided. For example, when we decompress the data, we certainly need a temporary storage place for the numbers to be returned, This is why the first line of inflate has a byte [] num = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; Statement. But think about it. This array is only used to store 8 bytes of long data. If long is used directly, it is equivalent to initializing an 8-byte array on the stack. What needs to be solved here is only how long operates the specified bytes. In fact, it is very simple here. We only need to move the corresponding byte to the left to the corresponding position. For example, we need to modify the second byte of long to 0x02. We only need the following operations:

    longData = (longData & ˜(0xff << 2 * 8)) | (0x02 << 2 * 8)

Another detail is that the value we take directly from the byte [] data is represented by a signed number. If we directly use the above formula, the displacement will be affected by the sign bit. Therefore, we need to use 0xff & byteary [i] to convert it into an unsigned number. Finally, the optimized inflate method is as follows:

private static long inflate(byte[] shard, int numPos, int len) {
-        byte[] num = {0, 0, 0 ,0 ,0 ,0, 0, 0};
+       long data = 0;

-       System.arraycopy(shard, numPos, num, num.length - len, len);
+       for (int i = 0; i < len; i++) {
+           data |= (long) Byte.toUnsignedInt(shard[numPos + i]) << (len - i - 1) * 8;
+       }

-       int i = num.length - len;
-       int negative = num[i] & 0x10;
+       // View symbol bits
+       long negative = data & (0x10L << (len - 1) * 8);

-       num[i] &= 0x0f;
-       num[i] |= negative << 63;
+       // Clear occupied bit data
+       data &= ~(0xf0L << (len - 1) * 8);

-       return negative > 0 ? -longFrom8Bytes(num) : longFrom8Bytes(num);
+       return negative > 0 ? -data : data;
}

After optimization, all heap data declarations have been removed, and there is an additional optimization, that is, before using the temporary array method, we also need to convert the array to long, that is, the role of the longFrom8Bytes method. Now we can return directly, and further optimize the effect. After testing, the performance is improved by 35% again, and the TPS is about 1250.

5 inline short function

Each function call requires a stack in and stack out operation, which is also time-consuming. In daily programs, these losses can be ignored, but they are amplified in this batch. Through the previous code, we can find that there is a updateOffset function in the get method. In fact, this function is very simple, which can be directly inlined, and there is one more line of code, As follows:

private void updateOffset() {
            byte[] shard = shards[shardIndex];

            // Find the offset of the corresponding data
            int len = (0xff & shard[0]) >>> 5;

            curOffset = inflate(shard, 0, len);
}

We inline it as follows:

if (numPos >= shard.length) {
                shardIndex++;
                numPos = 0;

-              updateOffset();
                // Find the offset of the corresponding data
+              shard = shards[shardIndex];
+              curOffset = inflate(shard, 0, (0xff & shard[0]) >>> 5);
}

There are also some, such as byte To unsigned int (int) is a simple line of code, which can be copied directly without method calls.

Three properties

Finally, the TPS of our batch interface has been upgraded to about 1380, which has been nearly 20 times higher than the initial 72. Although there is still some performance gap compared with the original array, it is also on the same order of magnitude. According to the calculation that the batch is enlarged by 5w, the TPS obtained in a single order has reached 6500w, and the random single get has also reached 260w TPS, which is fully enough to meet the production needs.

IV. optimization summary

From the above optimization, we can conclude that:

1. Java basic type data structure is much faster than object structure. The more oriented to the bottom, the faster
2. The allocation of data on the heap is very slow, and high-frequency calls will frequently trigger Yong GC, which has a great impact on the execution speed, so the stack can never use the heap
3. Object calls are slower than direct operations because they need to go up and down the stack. Therefore, if it is a few lines of simple calls, it will be much faster to directly copy and call out the logic, such as byte Tounsignedint() - of course, this is under extreme performance
4. Reduce intermediate data and temporary variables
5. Any small performance loss will multiply in huge calls, so be careful with batch interfaces

Original link
This article is the original content of Alibaba cloud and cannot be reproduced without permission.