A thorough understanding of sorting algorithms

Classification: algorithm 2013-09-26 22:20  61 people read comment(0)  Collection  Report

There is a little obsessive-compulsive disorder, always feel like writing on the reprint, so that the headline is black is very annoying, but still to share!

Change from: sort

1. Bubbler Sort

I just said a bad word about bubble sort, but bubble sort also has its advantages, that is, easy to understand, stable, and low space complexity, no need to create additional elements of the temporary save control array, of course, it is easy to write.

The algorithm is very simple. It compares two adjacent values of the array, and "pops" large bubbles into the back of the array. It divides the square of N by so many comparisons and exchanges (N is the element of the array). Its complexity is (n_), as shown in the figure:

 

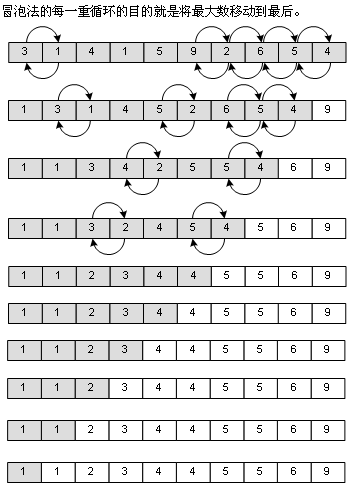
2. Straight Insertion Sort

Bubble method is no longer accessible to the ordered part (the white background part of the array shown in the figure above), but insertion sort is necessary, because its method is to take an element from the unordered part and insert it into the ordered part. The insertion position is from back to front, so that if the array itself is ordered (in order). The speed will be very fast, but in turn, if the array itself is in reverse order, the speed will be very slow, as shown in the figure:

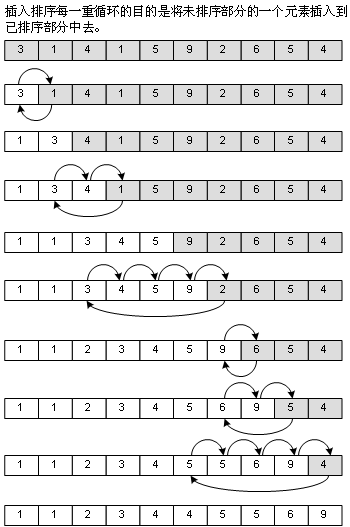
3. Binary Insertion Sort

This is an improvement on direct insertion sort. Because the ordered parts are ordered, we can use binary search to determine our insertion location, not one by one. Apart from this, it is no different from insertion sort. As for binary search, see my previous article (the fourth article in this series). The figure is no different from the figure above. The difference is that the insertion position is determined, but the performance can be improved a lot. (Performance analysis will be mentioned later)

4. Straight Selection Sort

This is the sort method that I can think of before I learn the data structure. The idea is very simple. I use the way of rolling table to find the biggest element and exchange it with the last element. Then I start from scratch to find the largest one from the first element to the N-1 element and exchange it with the N-1 element. In fact, it is almost the idea of bubbling method, but there are fewer elements to move in the whole process than bubbling method, so the performance is better than bubbling method. Look at the picture: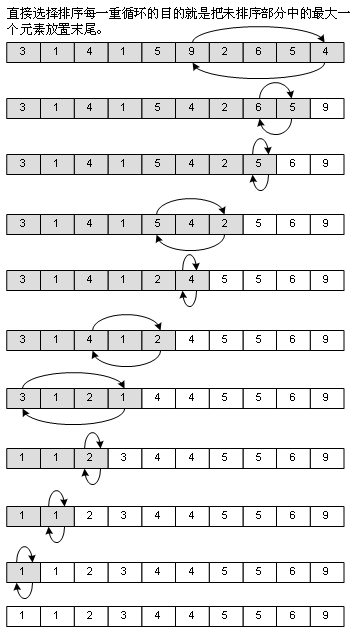

Quick Sort

Quick sorting is a very good sorting algorithm, beginners may find it a little difficult to understand, in fact, it is a "divide and conquer" idea, the big is divided into small, small and then divided into smaller, so you can see very clearly from the code in a moment, using recursion. As shown in the picture:

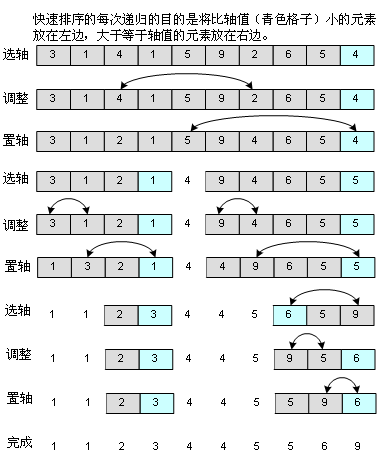
One of them is to choose an axis value, which ideally is the central axis. The role of the central axis is to make the element on its left smaller than it, and the element on its right not less than it. (I used "no less than" instead of "greater" to take into account the duplication of element values, which can also be seen in the code. If the ">=" operator is replaced by ">", there will be problems.) Of course, if the mid-axis is not well selected and the largest element or the smallest element is selected, the situation will be worse. I choose the axle value by taking out the first element, the middle one. Elements and the last element, and then select the intermediate value from these three elements, which can handle most situations.

6. Improved Quick Sort

The disadvantage of quick sorting is the use of recursion. If the amount of data is large, will a large number of recursive calls lead to performance degradation? I think so, so I'm going to do this optimization. Considering the small amount of data, the performance of direct selection sort is almost the same as that of quick sort. When the number of elements of subarray is less than 30, I use direct selection sort. Will this improve the performance a little? I will analyze it later. The sorting process can refer to the previous two graphs, so I won't draw another one.

7. Bucket Sort

This is by far the fastest sort method, its time complexity is only(n), that is, linear complexity! Isn't it amazing? But it is conditional. For example, the number of National College Entrance Examination candidates in one year is 5 million. The scores are based on standard scores, with a minimum of 100 and a maximum of 900. There are no decimals. You can arrange these 5 million yuan elements in an array. We grasp this very special condition, and can complete the 5 million ranking in milliseconds. That is: the lowest 100, the highest 900, no decimal, how many kinds of scores can be produced? There are 900 - 100 + 1 = 801. So many kinds. Think about it. Is there any way of "speculation and ingenuity"? The method is to create 801 "barrels", traverse the array from beginning to end, and feed different "barrels" with different scores. For example, one examinee scored 500 points, then add 1 to the barrel with 500 points (subscript 500-100). After completion, traverse the barrel array, according to the barrel value, fill in the original array, there are 1000 people with 100 points, so from 0 to 999, fill in 1000, 101 points. There are 1200 people, so from 1000 to 2019, they all fill in 101... As shown in the picture:

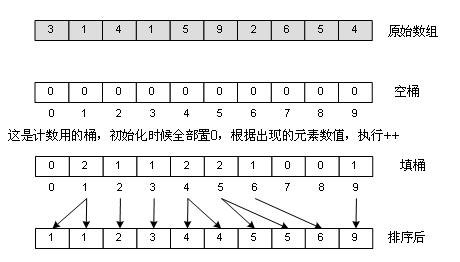
Obviously, if the score is not an integer from 100 to 900, but from 0 to 200 million, it is impossible to allocate 200 million barrels. Therefore, barrel sorting has its limitations, which is suitable for the case where the set of element values is not large.

Radix Sort

Cardinal sorting is an improvement on bucket sorting, which makes "bucket sorting" suitable for a larger set of element values, rather than improving performance. The idea is that, for example, the set of values is an 8-bit integer, and it's difficult to create 100 million buckets. So we first sort the bits of these numbers in a bucket-like order (hereinafter referred to as "bucket-like sort"), and then sort the ten bits of these numbers in a bucket-like order, then a hundred bits... It's done eight times. Of course, I'm talking about ideas. In fact, we don't usually do that. Because C++ is a fast displacement operator, we usually sort buckets in bytes. But for the convenience of drawing, I sort the buckets in half bytes (4 bit s), because the buckets in bytes are 256 barrels, which is a bit difficult to draw, as shown in the figure:

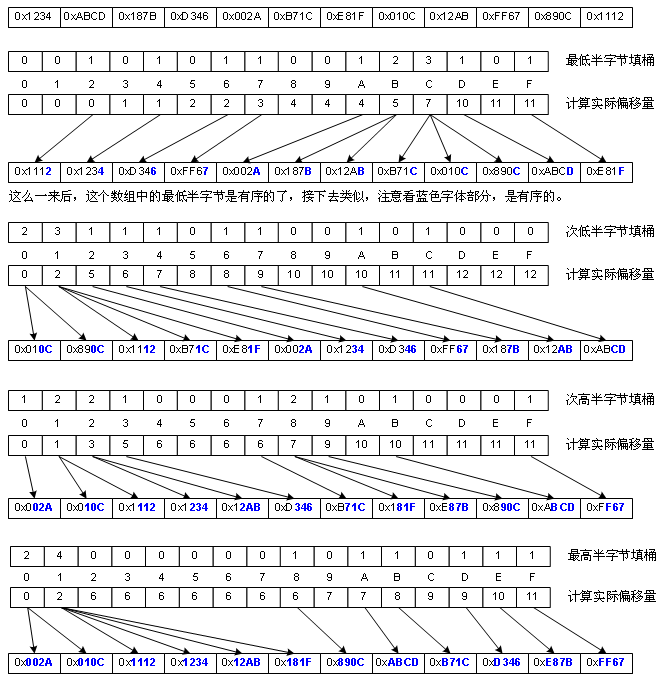
Cardinal sorting is suitable for the case of wide numerical distribution, but because of the need to allocate an additional temporary space as large as the original array, its processing is also limited. For the large number of elements of the original array, the space overhead is large. In terms of performance, bucket sorting is not as good as bucket sorting because it requires several "bucket-like sorting". But its complexity is the same as barrel sorting, also(n), although it uses multiple loops, but there is no nesting of loops.

9. Performance analysis and summary

The first six algorithms are bubbling, direct insertion, dichotomous insertion, direct selection, fast sorting and improved fast sorting.

My analysis process is not complicated. I try to generate a random array with a numerical range of 0 to 7 FFF. This can be filled with random numbers generated by rand() of C++ random function. Then I try different lengths of arrays. I try 10 times for the same length of arrays to get the average value and avoid excessive fluctuations. Finally, I use Excel to analyze the results, OK, as shown above.

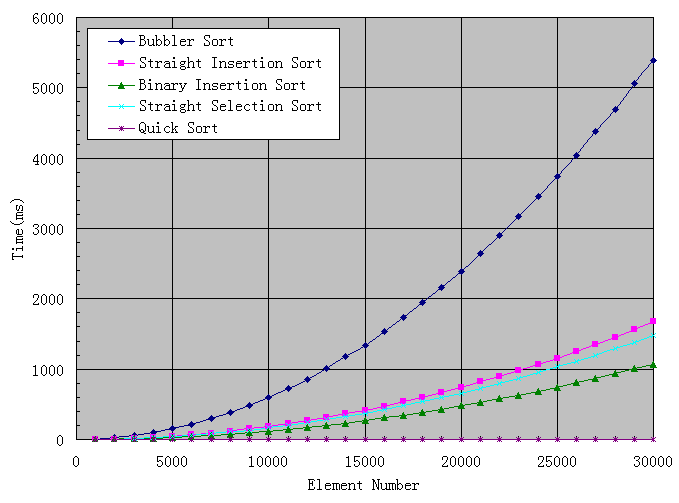
At the worst glance, it's bubbles. Direct insertion is comparable to direct selection, but I prefer direct selection because the idea is simple, the elements that need to be moved are relatively small, and the speed is slightly faster. From the figure, the speed of dichotomy insertion is much faster than that of direct insertion, but the code is slightly longer.

Surprisingly, the time consumed by quick sorting within 30,000 points is almost negligible, and the speed is exciting, while the improved fast sorting line overlaps with the fast sorting, so it is not drawn. It seems that to do a separate analysis of quick sorting, I increased the number of array elements from 50,000 to 1.5 million, and drew the following figure:

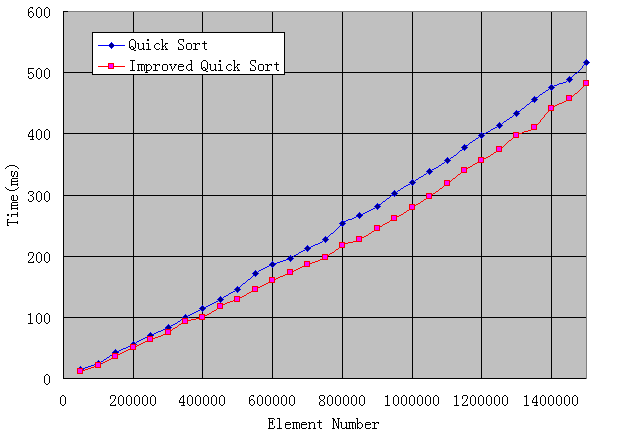
It can be seen that even at 1.5 million points, the two kinds of quick sorting can be completed in about half a second. It's really fast. The performance of the improved quick sorting has improved slightly, but it's not obvious. Can you see from the graph that the minimum number of quick sorting elements I set is not appropriate? But I tried several values that were almost the same.

Finally, looking at the sort of linear complexity, the speed is amazing. I tested from 400,000 to 12 million, and the results are as follows:

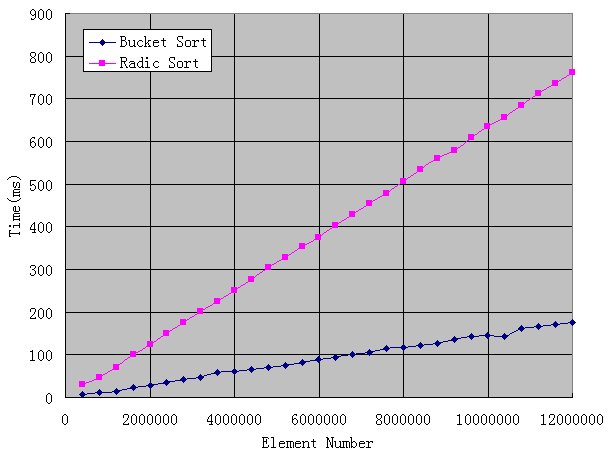
It can be seen that with a slight adjustment of the algorithm, the speed can be improved qualitatively, instead of what we thought before: no matter how fast it will be, it will not be much faster than the bubble method.

I ended up making a table to compare these sorting methods:

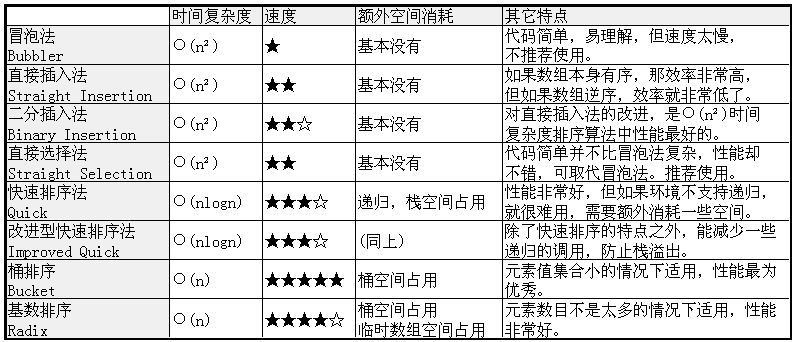
And one last thing: Attach my code.

1. #include "stdio.h"  
2. #include "stdlib.h"  
3. #include "time.h"  
4. #include "string.h"  
5.   
6. void BubblerSort(int *pArray, int iElementNum);  
7. void StraightInsertionSort(int *pArray, int iElementNum);  
8. void BinaryInsertionSort(int *pArray, int iElementNum);  
9. void StraightSelectionSort(int *pArray, int iElementNum);  
10. void QuickSort(int *pArray, int iElementNum);  
11. void ImprovedQuickSort(int *pArray, int iElementNum);  
12. void BucketSort(int *pArray, int iElementNum);  
13. void RadixSort(int *pArray, int iElementNum);  
14.   
15. //Tool functions.  
16. void PrintArray(int *pArray, int iElementNum);  
17. void StuffArray(int *pArray, int iElementNum);  
18.   
19. inline void Swap(int& a, int& b);  
20.   
21. #define SINGLE_TEST  
22.   
23. int main(int argc, char* argv[])  
24. {  
25.     srand(time(NULL));  
26. #ifndef SINGLE_TEST  
27.     int i, j, iTenTimesAvg;  
28.     for(i=50000; i<=1500000; i+=50000)  
29.     {  
30.         iTenTimesAvg = 0;  
31.         for(j=0; j<10; j++)  
32.         {  
33.             int iElementNum = i;  
34.             int *pArr = new int[iElementNum];  
35.             StuffArray(pArr, iElementNum);  
36.             //PrintArray(pArr, iElementNum);  
37.             clock_t ctBegin = clock();  
38.             ImprovedQuickSort(pArr, iElementNum);  
39.             //PrintArray(pArr, iElementNum);  
40.             clock_t ctEnd = clock();  
41.             delete[] pArr;  
42.   
43.             iTenTimesAvg += ctEnd-ctBegin;  
44.         }  
45.         printf("%d\t%d\n", i, iTenTimesAvg/10);  
46.     }  
47. #else  
48.     //Single test  
49.     int iElementNum = 100;  
50.     int *pArr = new int[iElementNum];  
51.     StuffArray(pArr, iElementNum);  
52.     PrintArray(pArr, iElementNum);  
53.     clock_t ctBegin = clock();  
54.     QuickSort(pArr, iElementNum);  
55.     clock_t ctEnd = clock();  
56.     PrintArray(pArr, iElementNum);  
57.     delete[] pArr;  
58.     int iTenTimesAvg = ctEnd-ctBegin;  
59.     printf("%d\t%d\n", iElementNum, iTenTimesAvg);  
60. #endif  
61.     return 0;  
62. }  
63.   
64. void BubblerSort(int *pArray, int iElementNum)  
65. {  
66.     int i, j, x;  
67.     for(i=0; i<iElementNum-1; i++)  
68.     {  
69.         for(j=0; j<iElementNum-1-i; j++)  
70.         {  
71.             if(pArray[j]>pArray[j+1])  
72.             {  
73.                 //Frequent swap calling may lower performance.  
74.                 //Swap(pArray[j], pArray[j+1]);  
75.   
76.                 //Do you think bit operation is better? No! Please have a try.  
77.                 //pArray[j] ^= pArray[j+1];  
78.                 //pArray[j+1] ^= pArray[j];  
79.                 //pArray[j] ^= pArray[j+1];  
80.                   
81.                 //This kind of traditional swap is the best.  
82.                 x = pArray[j];  
83.                 pArray[j] = pArray[j+1];  
84.                 pArray[j+1] = x;  
85.             }  
86.         }  
87.     }  
88. }  
89.   
90. void StraightInsertionSort(int *pArray, int iElementNum)  
91. {  
92.     int i, j, k;  
93.     for(i=0; i<iElementNum; i++)  
94.     {  
95.         int iHandling = pArray[i];  
96.         for(j=i; j>0; j--)  
97.         {  
98.             if(iHandling>=pArray[j-1])  
99.                 break;  
100.         }  
101.   
102.         for(k=i; k>j; k--)  
103.             pArray[k] = pArray[k-1];  
104.         pArray[j] = iHandling;  
105.     }  
106. }  
107.   
108. void BinaryInsertionSort(int *pArray, int iElementNum)  
109. {  
110.     int i, j, k;  
111.     for(i=0; i<iElementNum; i++)  
112.     {  
113.         int iHandling = pArray[i];  
114.           
115.         int iLeft = 0;  
116.         int iRight = i-1;  
117.         while(iLeft<=iRight)  
118.         {  
119.             int iMiddle = (iLeft+iRight)/2;  
120.             if(iHandling < pArray[iMiddle])  
121.             {  
122.                 iRight = iMiddle-1;  
123.             }  
124.             else if(iHandling > pArray[iMiddle])  
125.             {  
126.                 iLeft = iMiddle+1;  
127.             }  
128.             else  
129.             {  
130.                 j = iMiddle + 1;  
131.                 break;  
132.             }  
133.         }  
134.   
135.         if(iLeft>iRight)  
136.             j = iLeft;  
137.           
138.         for(k=i; k>j; k--)  
139.             pArray[k] = pArray[k-1];  
140.         pArray[j] = iHandling;  
141.     }  
142. }  
143.   
144. void StraightSelectionSort(int *pArray, int iElementNum)  
145. {  
146.     int iEndIndex, i, iMaxIndex, x;  
147.   
148.     for(iEndIndex=iElementNum-1; iEndIndex>0; iEndIndex--)  
149.     {  
150.         for(i=0, iMaxIndex=0; i<iEndIndex; i++)  
151.         {  
152.             if(pArray[i]>=pArray[iMaxIndex])  
153.                 iMaxIndex = i;  
154.         }  
155.         x = pArray[iMaxIndex];  
156.         pArray[iMaxIndex] = pArray[iEndIndex];  
157.         pArray[iEndIndex] = x;  
158.     }      
159. }  
160.   
161. void BucketSort(int *pArray, int iElementNum)  
162. {  
163.     //This is really buckets.  
164.     int buckets[RAND_MAX];  
165.     memset(buckets, 0, sizeof(buckets));  
166.     int i;  
167.     for(i=0; i<iElementNum; i++)  
168.     {  
169.         ++buckets[pArray[i]-1];  
170.     }  
171.   
172.     int iAdded = 0;  
173.     for(i=0; i<RAND_MAX; i++)  
174.     {  
175.         while((buckets[i]--)>0)  
176.         {  
177.             pArray[iAdded++] = i;  
178.         }  
179.     }  
180. }  
181.   
182. void RadixSort(int *pArray, int iElementNum)  
183. {  
184.     int *pTmpArray = new int[iElementNum];  
185.   
186.     int buckets[0x100];  
187.     memset(buckets, 0, sizeof(buckets));  
188.     int i;  
189.     for(i=0; i<iElementNum; i++)  
190.     {  
191.         ++buckets[(pArray[i])&0xFF];  
192.     }  
193.       
194.     //Convert number to offset  
195.     int iPrevNum = buckets[0];  
196.     buckets[0] = 0;  
197.     int iThisNum;  
198.     for(i=1; i<0x100; i++)  
199.     {  
200.         iThisNum = buckets[i];  
201.         buckets[i] = buckets[i-1] + iPrevNum;  
202.         iPrevNum = iThisNum;  
203.     }  
204.   
205.     for(i=0; i<iElementNum; i++)  
206.     {  
207.         pTmpArray[buckets[(pArray[i])&0xFF]++] = pArray[i];  
208.     }  
209.   
210.     //////////////////////////////////////////////////////////////////////////  
211.     memset(buckets, 0, sizeof(buckets));  
212.     for(i=0; i<iElementNum; i++)  
213.     {  
214.         ++buckets[(pTmpArray[i]>>8)&0xFF];  
215.     }  
216.   
217.     //Convert number to offset  
218.     iPrevNum = buckets[0];  
219.     buckets[0] = 0;  
220.     iThisNum;  
221.     for(i=1; i<0x100; i++)  
222.     {  
223.         iThisNum = buckets[i];  
224.         buckets[i] = buckets[i-1] + iPrevNum;  
225.         iPrevNum = iThisNum;  
226.     }  
227.   
228.     for(i=0; i<iElementNum; i++)  
229.     {  
230.         pArray[buckets[((pTmpArray[i]>>8)&0xFF)]++] = pTmpArray[i];  
231.     }  
232.   
233.     delete[] pTmpArray;  
234. }  
235.   
236. void QuickSort(int *pArray, int iElementNum)  
237. {  
238.     int iTmp;  
239.   
240.     //Select the pivot make it to the right side.  
241.     int& iLeftIdx = pArray[0];  
242.     int& iRightIdx = pArray[iElementNum-1];  
243.     int& iMiddleIdx = pArray[(iElementNum-1)/2];  
244.     if(iLeftIdx>iMiddleIdx)  
245.     {  
246.         iTmp = iLeftIdx;  
247.         iLeftIdx = iMiddleIdx;  
248.         iMiddleIdx = iTmp;  
249.     }  
250.     if(iRightIdx>iMiddleIdx)  
251.     {  
252.         iTmp = iRightIdx;  
253.         iRightIdx = iMiddleIdx;  
254.         iMiddleIdx = iTmp;  
255.     }  
256.     if(iLeftIdx>iRightIdx)  
257.     {  
258.         iTmp = iLeftIdx;  
259.         iLeftIdx = iRightIdx;  
260.         iRightIdx = iTmp;  
261.     }  
262.   
263.     //Make pivot's left element and right element.  
264.     int iLeft = 0;  
265.     int iRight = iElementNum-2;  
266.     int& iPivot = pArray[iElementNum-1];  
267.     while (1)  
268.     {  
269.         while (iLeft<iRight && pArray[iLeft]<iPivot) ++iLeft;  
270.         while (iLeft<iRight && pArray[iRight]>=iPivot) --iRight;  
271.         if(iLeft>=iRight)  
272.             break;  
273.         iTmp = pArray[iLeft];  
274.         pArray[iLeft] = pArray[iRight];  
275.         pArray[iRight] = iTmp;  
276.     }  
277.   
278.     //Make the i  
279.     if(pArray[iLeft]>iPivot)  
280.     {  
281.         iTmp = pArray[iLeft];  
282.         pArray[iLeft] = iPivot;  
283.         iPivot = iTmp;  
284.     }  
285.   
286.     if(iLeft>1)  
287.         QuickSort(pArray, iLeft);  
288.   
289.     if(iElementNum-iLeft-1>=1)  
290.         QuickSort(&pArray[iLeft+1], iElementNum-iLeft-1);  
291.   
292. }  
293.   
294. void ImprovedQuickSort(int *pArray, int iElementNum)  
295. {  
296.     int iTmp;  
297.       
298.     //Select the pivot make it to the right side.  
299.     int& iLeftIdx = pArray[0];  
300.     int& iRightIdx = pArray[iElementNum-1];  
301.     int& iMiddleIdx = pArray[(iElementNum-1)/2];  
302.     if(iLeftIdx>iMiddleIdx)  
303.     {  
304.         iTmp = iLeftIdx;  
305.         iLeftIdx = iMiddleIdx;  
306.         iMiddleIdx = iTmp;  
307.     }  
308.     if(iRightIdx>iMiddleIdx)  
309.     {  
310.         iTmp = iRightIdx;  
311.         iRightIdx = iMiddleIdx;  
312.         iMiddleIdx = iTmp;  
313.     }  
314.     if(iLeftIdx>iRightIdx)  
315.     {  
316.         iTmp = iLeftIdx;  
317.         iLeftIdx = iRightIdx;  
318.         iRightIdx = iTmp;  
319.     }  
320.       
321.     //Make pivot's left element and right element.  
322.     int iLeft = 0;  
323.     int iRight = iElementNum-2;  
324.     int& iPivot = pArray[iElementNum-1];  
325.     while (1)  
326.     {  
327.         while (iLeft<iRight && pArray[iLeft]<iPivot) ++iLeft;  
328.         while (iLeft<iRight && pArray[iRight]>=iPivot) --iRight;  
329.         if(iLeft>=iRight)  
330.             break;  
331.         iTmp = pArray[iLeft];  
332.         pArray[iLeft] = pArray[iRight];  
333.         pArray[iRight] = iTmp;  
334.     }  
335.       
336.     //Make the i  
337.     if(pArray[iLeft]>iPivot)  
338.     {  
339.         iTmp = pArray[iLeft];  
340.         pArray[iLeft] = iPivot;  
341.         iPivot = iTmp;  
342.     }  
343.       
344.     if(iLeft>30)  
345.         ImprovedQuickSort(pArray, iLeft);  
346.     else  
347.         StraightSelectionSort(pArray, iLeft);  
348.       
349.     if(iElementNum-iLeft-1>=30)  
350.         ImprovedQuickSort(&pArray[iLeft+1], iElementNum-iLeft-1);  
351.     else  
352.         StraightSelectionSort(&pArray[iLeft+1], iElementNum-iLeft-1);  
353. }  
354.   
355. void StuffArray(int *pArray, int iElementNum)  
356. {  
357.     int i;  
358.     for(i=0; i<iElementNum; i++)  
359.     {  
360.         pArray[i] = rand();  
361.     }  
362. }  
363.   
364. void PrintArray(int *pArray, int iElementNum)  
365. {  
366.     int i;  
367.     for(i=0; i<iElementNum; i++)  
368.     {  
369.         printf("%d ", pArray[i]);  
370.     }  
371.     printf("\n\n");  
372. }  
373.   
374. void Swap(int& a, int& b)  
375. {  
376.     int c = a;  
377.     a = b;  
378.     b = c;  
379. }