Reprinted from: https://blog.csdn.net/chanmufeng/article/details/82955730

0-1 knapsack problem

The 0-1 knapsack problem is that each item can only be used once.

Recursive Method

public class KnapSack01 {
    /**
     * Recursive Function for Solving Knapsack Problem
     *
     * @param w        Weight Array of Items
     * @param v        Value Array of Items
     * @param index    Index of current items to be selected
     * @param capacity Current Backpack Effective Capacity
     * @return Maximum value
     */
    private static int solveKS(int[] w, int[] v, int index, int capacity) {
        //Baseline condition: If the index is invalid or insufficient, return the current value 0 directly.
        if (index < 0 || capacity <= 0)
            return 0;

        //The Value of Indix Items
        int res = solveKS(w, v, index - 1, capacity);
        //The value gained by placing item number index (provided that item number index can be put down)
        if (w[index] <= capacity) {
            res = Math.max(res, v[index] + solveKS(w, v, index - 1, capacity - w[index]));
        }
        return res;
    }

    public static int knapSack(int[] w, int[] v, int C) {
        int size = w.length;
        return solveKS(w, v, size - 1, C);
    }

    public static void main(String[] args){
        int[] w = {2,1,3,2};
        int[] v = {12,10,20,15};
        System.out.println(knapSack(w,v,5));
    }
}

Memorized Search

We can easily implement the above code by recursive method, but there is a serious problem that the direct use of top-down recursive algorithm will lead to more than once solving common sub-problems, so the efficiency is quite low.
We can save the results of the sub-problems that have been solved so that the sub-problems can be solved only once, which is called memory search.
Following is a memory search based on the above code

public class KnapSack01 {
    private static int[][] memo;

    /**
     * Recursive Function for Solving Knapsack Problem
     *
     * @param w        Weight Array of Items
     * @param v        Value Array of Items
     * @param index    Index of current items to be selected
     * @param capacity Current Backpack Effective Capacity
     * @return Maximum value
     */
    private static int solveKS(int[] w, int[] v, int index, int capacity) {
        //Baseline condition: If the index is invalid or insufficient, return the current value of 0 directly.
        if (index < 0 || capacity <= 0)
            return 0;

        //If this sub-problem has been solved, the result of the last solution will be returned directly.
        if (memo[index][capacity] != 0) {
            return memo[index][capacity];
        }

        //The Value of Indix Items
        int res = solveKS(w, v, index - 1, capacity);
        //The value gained by placing item number index (provided that item number index can be put down)
        if (w[index] <= capacity) {
            res = Math.max(res, v[index] + solveKS(w, v, index - 1, capacity - w[index]));
        }
        //Adding the solution of the sub-problem to facilitate the next direct use
        memo[index][capacity] = res;
        return res;
    }

    public static int knapSack(int[] w, int[] v, int C) {
        int size = w.length;
        memo = new int[size][C + 1];
        return solveKS(w, v, size - 1, C);
    }

    public static void main(String[] args) {
        int[] w = {2, 1, 3, 2};
        int[] v = {12, 10, 20, 15};
        System.out.println(knapSack(w, v, 5));
    }
}

dynamic programming algorithm

public class KnapSack01 {
    public static int knapSack(int[] w, int[] v, int C) {
        int size = w.length;
        if (size == 0) {
            return 0;
        }

		//dp[i][j] represents the maximum storage capacity of the first I items that J can store.
        int[][] dp = new int[size][C + 1];
        //Initialize the first line
        //Consider only the case where the backpack with a capacity of C holds item 0.
        for (int i = 0; i <= C; i++) {
            dp[0][i] = w[0] <= i ? v[0] : 0;
        }
		//Fill in other rows and columns
        for (int i = 1; i < size; i++) {
            for (int j = 0; j <= C; j++) {
                dp[i][j] = dp[i - 1][j]; //No Item i
                if (w[i] <= j) { //You can put Item i and Item i in it.
                    dp[i][j] = Math.max(dp[i][j], v[i] + dp[i - 1][j - w[i]]);
                }
            }
        }
        return dp[size - 1][C];
    }

    public static void main(String[] args) {
        int[] w = {2, 1, 3, 2};
        int[] v = {12, 10, 20, 15};
        System.out.println(knapSack(w, v, 5));
    }
}

Extreme optimization of spatial complexity

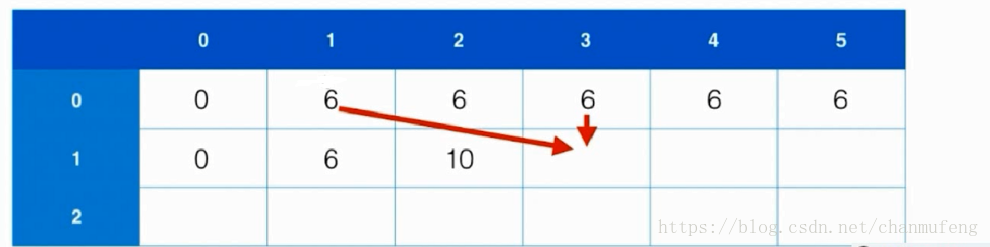
The above dynamic programming algorithm uses O(n*C) space complexity (because we use two-dimensional arrays to record the solution of sub-problems). In fact, we can only use one-dimensional arrays to store the results, but at the same time we need to note that in order to prevent the results from being overwritten, we have to calculate separately from the back to the front.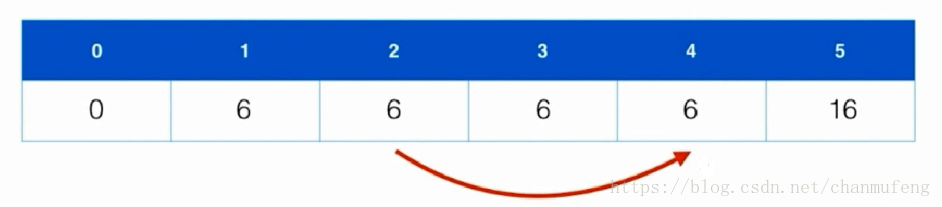

We still assume that the backpack space is 5, according to
F(i,C)=max(F(i−1,C),v(i)+F(i−1,C−w(i))) F(i,C)=max(F(i-1,C),v(i)+F(i-1,C-w(i)))
F(i,C)=max(F(i−1,C),v(i)+F(i−1,C−w(i)))
As we can see, when we use one-dimensional arrays to memorize, we only need to use the value of the current location and the value before that location, for example.
Suppose we want to calculate F(i,4) F(i,4)F(i,4), we need to use the values F(i_1,4) F(i-1,4)F(i_1, 4) and F(i_1, 4_w(i)) F(i-1,4-w(i))F(i_1, 4_w(i)) F(i_1, 4_w (i). So in order to prevent the results from being covered, we need to compute the results from backward to forward.
The final dynamic programming code is as follows

public class KnapSack01 {
    public static int knapSack(int[] w, int[] v, int C) {
        int size = w.length;
        if (size == 0) {
            return 0;
        }

        int[] dp = new int[C + 1];
        //Initialize the first line
        //Consider only the case where the backpack with a capacity of C holds item 0.
        for (int i = 0; i <= C; i++) {
            dp[i] = w[0] <= i ? v[0] : 0;
        }

        for (int i = 1; i < size; i++) {
            for (int j = C; j >= w[i]; j--) {
                dp[j] = Math.max(dp[j], v[i] + dp[j - w[i]]);
            }
        }
        return dp[C];
    }

    public static void main(String[] args) {
        int[] w = {2, 1, 3, 2};
        int[] v = {12, 10, 20, 15};
        System.out.println(knapSack(w, v, 5));
    }
}

Solving problems by using the idea of knapsack problem

leetcode 416 Partition Equal Subset Sum
Given a non-empty array containing only positive integers, determine whether the array can be divided into two parts, requiring the equality of the two parts.

problem analysis

This problem can be solved by using the idea of knapsack problem.

Assuming that a given number of elements is an array arr of n n n, the sum of array elements corresponds to the knapsack problem, which is equivalent to n n n items. The weight and value of each item are arr[i], and the weight limit of the knapsack is sum/2. How much is the maximum value of the items i n the knapsack?

class Solution {
    private boolean knapSack(int[] nums,int sum){
        int size = nums.length;
        
        boolean[] dp = new boolean[sum + 1];
        for (int i = 0;i <= sum;i ++){
           dp[i] = i == nums[0];
        }
        
        for (int i = 1;i < size;i++){
            for (int j = sum;j >= nums[i];j--){
                dp[j] = dp[j] || dp[j-nums[i]];
            }
        }
        return dp[sum];
    }
    
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int item : nums){
            sum += item;
        }
        
        //If the array element is not a multiple of 2, return false directly
        if (sum % 2 != 0)
            return false;
        
        return knapSack(nums,sum/2);
    }
}