[actual combat] valid parentheses of LeetCode illustrated by ACM players

Hello, everyone. I'm handsome.

Today, let's judge whether the brackets are valid.

I don't know what to say. Let's start the whole thing.

LeetCode 20: valid parentheses

meaning of the title

Given a string s that only includes' (',') ',' {','} ',' [','] ', judge whether the string is valid.

Examples

Input: s = "() [] {}"

Output: true

Input: s = "([)]"

Output: false

Tips

Valid strings must meet:

The left parenthesis must be closed with the same type of right parenthesis
The left parentheses must be closed in the correct order

1 <= s.length <= 10^4

s consists only of parentheses () [] {}

Topic analysis

Bracket matching is a classic problem solved by using stack, which is difficult and simple.

I'm not very good at smelly treasure. Look at the link below. It's written by Ben egg:

Come on! Stack, queue!

After reading the stack, you will basically know more than half of this problem, and the remaining half is to move the cerebellar bag melon and think a little.

This problem is to maintain a stack. When you encounter the left bracket, you will enter the stack. When you encounter the right bracket, you will take out the top element of the stack and judge whether the top element of the stack matches the right bracket.

If there is no match, return false. If there is a match, repeat the above steps until the string is traversed.

It should be noted that two special cases also return false:

Traverse the entire string, the stack is not empty, indicating that there are more left parentheses.
The right parenthesis is encountered, but the stack is empty at this time, indicating that there are more right parentheses.

Except for the above situation, the rest will return true.

graphic

Assume s = "() [] {}"

Initialize first.

# initialization
stack = []

pairs = {
    ')': '(',
    ']': '[',
    '}': '{'
}

According to the "topic analysis", the left bracket is pushed into the stack, so in step 1, "(" is pushed into the stack

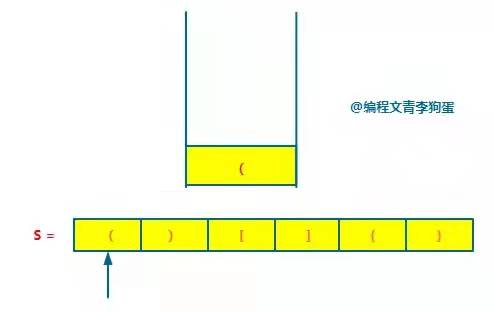
for i in s:
    # If it is an open bracket, press it into the stack
    if i not in pairs:
        stack.append(i)

Next, when you encounter the closing bracket ")", take out the stack top element "(", judge whether the stack top element is paired with the current closing bracket, and find the pairing.

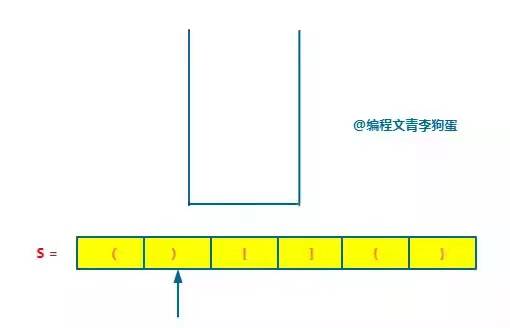
Since it matches, continue to the next step. Next, encounter the left bracket "[", and put it on the stack.

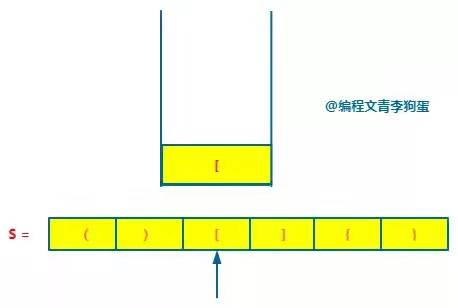
Next, when you encounter the closing bracket "]", take out the stack top element "[", judge whether the stack top element is paired with the current closing bracket, and find the pairing.

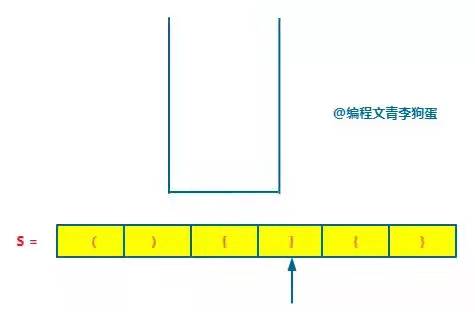
Since it matches again, continue to the next step. Next, encounter the left bracket "{" and put it on the stack.

Next, when you encounter the right bracket "}", take out the stack top element "{", judge whether the stack top element is paired with the current right bracket, and it is found that it is paired.

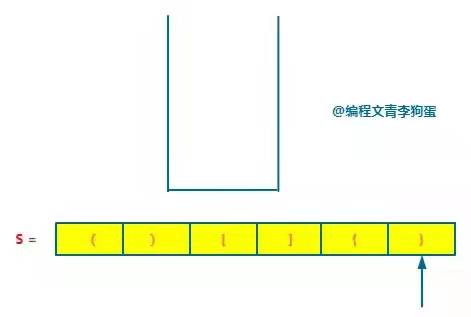
At this time, all strings are traversed, and the stack is empty. The string s is valid and returns true.

 return not stack

Let's assume that s = "([)]"

The first two elements are left parentheses, so they are directly put on the stack.

Next, when you encounter the closing bracket ")", take out the stack top element "[", the stack top element does not match the closing bracket, and return false.

# In the process of traversal, if an empty stack or mismatched parentheses are encountered, False is returned.
elif not stack or pairs[i] != stack.pop():
    return False

The operation of entering or leaving the stack of each element is O(1). In the worst case, each element will enter and only enter the stack once, so the time complexity is O(1) * n = O(n).

Similarly, in the worst case, all elements are stacked, so the space complexity is also O(n).

code implementation

Python code implementation

class Solution:
    def isValid(self, s: str) -> bool:

        # The string has an odd number of elements and does not match
        if len(s) % 2 == 1:
            return False

        # Initialization stack
        stack = []

        pairs = {
            ')': '(',
            ']': '[',
            '}': '{'
        }

        for i in s:
            # If it is an open bracket, press it into the stack
            if i not in pairs:
                stack.append(i)
            # In the process of traversal, if an empty stack or mismatched parentheses are encountered, False is returned.
            elif not stack or pairs[i] != stack.pop():
                return False

        # After traversing all, if the stack is empty, return True; if the stack is not empty, return False
        return not stack

Java code implementation

class Solution {
    public boolean isValid(String s) {
        Deque<Character> deque = new LinkedList<>();
        char ch;
        for (int i = 0; i < s.length(); i++) {
            ch = s.charAt(i);
            //When you encounter the left bracket, put the corresponding right bracket on the stack
            if (ch == '(') {
                deque.push(')');
            }else if (ch == '{') {
                deque.push('}');
            }else if (ch == '[') {
                deque.push(']');
            } else if (deque.isEmpty() || deque.peek() != ch) {
                return false;
            }else {//If it is a right parenthesis, judge whether it matches the top element of the stack
                deque.pop();
            }
        }
        //Finally, determine whether the elements in the stack match
        return deque.isEmpty();
    }
}

The valid parentheses of the diagram end here.

The first practical question of the stack is relatively simple. There must be no problem in writing, painting and careful thinking.

See this is true love, remember to praise it.

I'm handsome. I'll see you next time!

Keywords: Python Java data structure leetcode stack

Added by ccx004 on Sun, 20 Feb 2022 09:42:30 +0200

Programming VIP