Title address:

https://www.acwing.com/problem/content/description/1127/

Farmer John's farm has many pastoral areas, and some paths connect some specific pastoral areas. A pastoral area with all the connections is called a pasture. But for now, you can see that at least two pastoral areas are not connected. Now, John wants to add a path to the farm (note that it happens to be one). The diameter of a pasture is the distance between the two farthest pastoral areas in the pasture (all the distances mentioned in this topic refer to the shortest distance). Consider the following two pastures, each of which has its own coordinates:

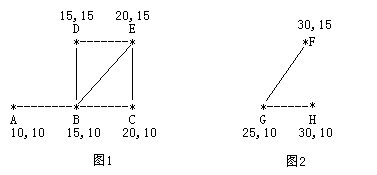
chart 1 1 1 yes 5 5 For pastures in 5 pastoral areas, the pastoral area is represented by * and the path is represented by a straight line. chart 1 1 The diameter of the pasture shown in 1 is about 5 + 5 2 = 12.07106 5+5\sqrt{2}=12.07106 5+52 = 12.07106, the two farthest pastoral areas are A A A and E E E. The shortest path between them is A − B − E A-B-E A−B−E. chart 2 2 2 is another ranch. Both farms are on John's ranch. John will choose one pastoral area from each of the two pastures, and then connect them with a path to make the new and larger pastures have the smallest diameter. Note that if two paths intersect halfway, we don't think they are connected. Only when two paths intersect in the same pastoral area, we think they are connected. Now please program to find a path connecting two different pastures, so that after connecting this path, the diameter of the pastures with the largest diameter among all pastures (generated new pastures and original pastures) is as small as possible. Output the minimum possible value of this diameter.

Input format:
The first 1 1 Line 1: an integer N N N. Indicates the number of pastoral areas; The first 2 2 2 to N + 1 N+1 N+1 line: two integers per line X , Y X,Y 10. Y, denotes N N Coordinates of N pastoral areas. The coordinates of each pastoral area are different. The first N + 2 N+2 Line N+2 to 2 ∗ N + 1 2*N+1 2 * N+1 line: each line includes N N N numbers( 0 0 0 or 1 1 1) Represents a symmetric adjacency matrix. For example, the matrix of two pastures in the title description is described as follows:

  A B C D E F G H 
A 0 1 0 0 0 0 0 0 
B 1 0 1 1 1 0 0 0 
C 0 1 0 0 1 0 0 0 
D 0 1 0 0 1 0 0 0 
E 0 1 1 1 0 0 0 0 
F 0 0 0 0 0 0 1 0 
G 0 0 0 0 0 1 0 1 
H 0 0 0 0 0 0 1 0

The input data includes at least two disconnected pastoral areas.

Output format:
Only one line, including a real number, represents the answer. The number retains six decimal places.

Data range:
1 ≤ N ≤ 150 1≤N≤150 1≤N≤150
0 ≤ X , Y ≤ 1 0 5 0≤X,Y≤10^5 0≤X,Y≤105

The idea is to directly enumerate two pastoral areas that are not in the same pasture, connect them, and see what is the smallest diameter you can get. The smallest diameter may be the diameter of a pasture or the diameter of a new pasture after connection. The diameter of the new pasture should be the two points connected a a a and b b b distance, plus a a a distance from the farthest point in the same pasture, plus b b b distance from the farthest point in the same pasture. Therefore, the Euclidean distance between two points with a road can be calculated when reading in, and then the distance between each two points can be calculated by Floyd algorithm. At the same time, the distance between each point and its farthest point in the connected block can be preprocessed. Finally, enumerate all possible cases and find a minimum value. Floyd algorithm reference https://blog.csdn.net/qq_46105170/article/details/113821689 . The code is as follows:

#include <iostream>
#include <cstring>
#include <cmath>

#define x first
#define y second
using namespace std;

typedef pair<int, int> PII;

const int N = 160;
const double INF = 1e20;
int n;
PII q[N];
char g[N][N];
double d[N][N], maxd[N];

double get_dist(PII a, PII b) {
    double dx = a.x - b.x, dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d%d", &q[i].x, &q[i].y);

    for (int i = 0; i < n; i++) cin >> g[i];

	// Find the Euclidean distance between two points with a road. If there is no road, it will be initialized to positive infinity
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            if (i != j) {
                if (g[i][j] == '0') d[i][j] = INF;
                else d[i][j] = get_dist(q[i], q[j]);
            }

	// Floyd algorithm finds the distance of all point pairs
    for (int k = 0; k < n; k++)
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

	// Preprocess the distance between each point and the farthest point in the same connected block
    for (int i = 0; i < n; i++) 
        for (int j = 0; j < n; j++)
            if (d[i][j] < INF)
                maxd[i] = max(maxd[i], d[i][j]);

	// The final answer may be the diameter of a pasture or the diameter of a new pasture. Find the two in turn
    double res1 = 0;
    for (int i = 0; i < n; i++)
        res1 = max(res1, maxd[i]);

    double res2 = INF;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            if (d[i][j] >= INF)
                res2 = min(res2, get_dist(q[i], q[j]) + maxd[i] + maxd[j]);

    printf("%lf\n", max(res1, res2));

    return 0;
}

Time complexity O ( n 3 ) O(n^3) O(n3), space O ( n 2 ) O(n^2) O(n2).