Knapsack problem ★★★
(1) 0-1 knapsack problem (1 for each item)
Topic introduction

sample input
4 5 1 2 2 4 3 4 4 5
output
8
[version 1] two dimensional state definition of 0-1 knapsack problem
- f[i][j]: select only the first I items with total volume < = Max of J
State analysis
(1) When the current backpack capacity is insufficient (J < v [i]), the i-th item cannot be selected, so the optimal solution of the first I items is the same as that of the first i - 1
- f[i][j] = f[i - 1][j]
(2) When the current backpack capacity is enough for the ith item (j ≥ v[i]), the ith item can be selected. Therefore, it is necessary to continue to decide whether to select or not the ith item
- Select: f[i][j] = f[i - 1][j - v[i] + w[i]
- Not selected: f[i][j] = f[i - 1][j]
- Finally, take Max
State transition equation:
f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i]
The C + + code is as follows
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N]; // volume
int w[N]; // weight
int f[N][N]; // DP array
// f[i][j]: select only the first I items, total volume < = J
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// 2D f[i][j]
for(int i = 1; i <= n; i++){
for (int j = 0; j <= m; j ++ ){
f[i][j] = f[i-1][j]; // Corresponding situation 1
if(j >= v[i]) // J-V [i] > = 0 corresponds to case 2 and makes a decision
f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
} // !!! f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i])
}
cout << f[n][m] <<endl;
return 0;
}
[version 2 - final version] one dimensional state of 0-1 knapsack problem
- When analyzing the two-dimensional state, the state of round i is only related to round i - 1, so the first dimension of the array can be removed
- [note]: in the process of traversing j in each round, i is unchanged (all in the state of round i),
However, the current state of round i needs the state of round i - 1, so it needs to be enumerated in reverse order
Take chestnuts for example:
If enumerated to: i = 3, j = 8, v[3] = 5, w[3] = 1
two-dimensional: dp[3][8] = max(dp[2][8], dp[2][3] + w[3]) At this time dp[2][8]and dp[2][3]Are the status values of the previous round
one-dimensional: dp[8] = max(dp[8], dp[3] + w[3]) Optimize one dimension, Need guarantee dp[8]and dp[3]Are the status values of the previous round
If sequential enumeration j: (The first i round) When j = 8 Time, j = 3 Already enumerated,
dp[3] It has been calculated, therefore dp[3] Is the first i Status of wheel, Not the second i-1 Status of wheel ×
If enumerating in reverse order j: (The first i round) When j = 8 Time, j = 3 Not enumerated yet
dp[3] Not calculated yet, therefore dp[3] Is the first i-1 Status of wheel √
The C + + code is as follows
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N]; // volume
int w[N]; // weight
int f[N]; // DP array
// f[j]: total volume < = J
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
// Optimization: one dimensional f [J] v [i] < = J < = v
for(int i = 1; i <= n; i++){
for(int j = m; j >= v[i]; j--){ // [note] j reverse order is required
f[j] = max(f[j], f[j-v[i]] + w[i]);
} //f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i])
}
cout << f[m] <<endl;
return 0;
}
(2) Complete knapsack problem (unlimited items for each item)
Title Description

sample input
4 5 1 2 2 4 3 4 4 5
output
10
State analysis
Violent Version (TLE)
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i-1][j - k*v[i]] + k*v[i]);
cout<< f[n][m] <<endl;
Therefore, the state transition equation needs to be optimized
Original: F [I, J] = max (f [I-1, J], f [I-1, J-V] + W, f [I-1, J-2 * V] + 2 * W, f [I-1, J-3 * V] + 3 * W,...)
∵ f [I, J-V] = max (- ----------- f [I-1, J-V], f [I-1, J-2 * V] + W, f [I-1, J-3 * V] + 2 * W,...)
From the above two formulas, the following recurrence relationship can be obtained:
- f[i][j] = max(f[i - 1][j], f[i][j - v] + w)
Compared with the two-dimensional transfer equation of 0-1 knapsack, only the subscripts are different
- f[i][j] = max(f[i - 1][j], f[i - 1][j - v] + w)
Version 2. Optimized two-dimensional equation of state
The code is as follows:
for(int i = 1; i <= n; i++){
for(int j = 0; j <= m; j++){
// F [i] [J] = max (f [I-1] [J], f [I-1] [J-V] + W) 0-1 Backpack
// f[i][j] = max(f[i-1][j], f[i][j-v] + w) complete Backpack
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
cout<< f[n][m] <<endl;
Version 3 - final version: one dimensional equation of state
- [note]: j sequential traversal
- Because the current state of f[j] in round i only needs the state of f[j - v] in round i
The complete code is as follows
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int n, m;
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++){
for(int j = v[i]; j <= m; j++){
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout<< f[m] <<endl;
return 0;
}
(3) Multiple knapsack problem (each item is limited to s)
Title Description

sample input
4 5 1 2 3 2 4 1 3 4 3 4 5 2
output
10
State analysis
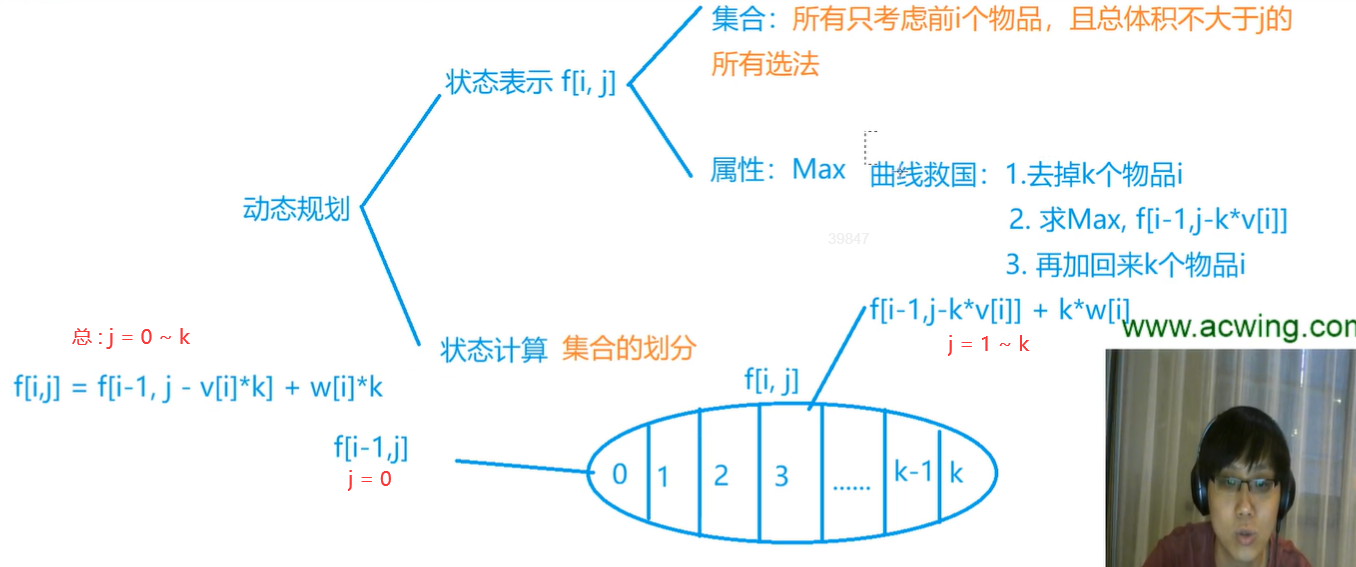
Version 1. Violence law
- State transition equation
f[i][j] = max(f[i-1][j-v[i] * k] + w[i] * k), K is the selected number, ranging from 0 to s[i]
- The code is as follows
for(int i = 1; i <= n; i++)
for (int j = 0; j <= m; j ++ )
for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i-1][j-v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
Version 2. Optimization using the idea of grouping binary
- Using the idea of grouping and binary optimization, the quantity s of each item is divided into 1, 2, 4, 2 ^ k, C log(s) + 1 group
The quantity s must be represented by a binary number to ensure that s = = 1 + 2 + 4 ++ 2^k + c

The code is as follows
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 24000, M = 2010;
int n, m;
int v[N], w[N], s[N];
int f[M];
int cnt = 0;
int main(){
cin >> n >> m;
int cnt = 0; //Number of groups
for(int i = 1; i <= n;i ++) {
int a, b, s;
cin >> a >> b >> s;
int k = 1; // Number in group
while(k <= s) {
cnt ++ ;
v[cnt] = a * k ; // V
w[cnt] = b * k; // W
s -= k; // s - 2^k
k *= 2; // k = k * 2
}
//The remaining group does not satisfy 2^k
if(s > 0) {
cnt ++ ;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
// for(int i = 1; i <= cnt; i++){
// cout << v[i] <<" "<< w[i] <<endl;
// }
// After grouping, each group is equivalent to an item in 0-1 backpack
// One dimensional optimization of 0-1 knapsack
for(int i = 1; i <= cnt; i++)
for(int j = m; j >= v[i]; j-- )
f[j] = max(f[j], f[j-v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
(4) Group knapsack problem (several in each group, only one in each group)
Title Description

sample input
3 5 2 1 2 2 4 1 3 4 1 4 5
output
8
State analysis
Select one from group i, and the total volume shall not exceed j
State transition equation:
f[i][j] = max(f[i-1][j], f[i-1][j-v[i][k]] + w[i][k])
[note]
- Because the state of round i depends on round i-1, when the optimization is one-dimensional, j needs to be in reverse order
- If the state of the i-th round only depends on the i-th round, when the optimization is one-dimensional, the j-order can be used
The code is as follows
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 105;
int f[N]; // f[i][j]: select one from group I, and the volume shall not exceed j
int v[N][N], w[N][N];
int s[N]; // Number of groups
int n, m;
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++){ // n: total number of groups
cin >> s[i]; // s[i]: number in the group
for(int j = 0; j < s[i]; j++){
cin >> v[i][j] >> w[i][j]; // [group i] [j]
}
}
for(int i = 1; i <= n; i++)
for(int j = m; j >= 0; j--)
for(int k = 0; k < s[i]; k++) // Number of traversal groups
if(v[i][k] <= j)
f[j] = max(f[j], f[j-v[i][k]] + w[i][k]);
cout << f[m] <<endl;
return 0;
}