Double pointer algorithm

We have already used the double pointer algorithm in quick sort and merge sort.

The first type: the first pointer points to sequence 1 and the second pointer points to sequence 2

The second type: two pointers point to the same sequence

for(int i=0,j=0;i<n;i++){
	while(j<i && check(i,j))
		j++;
	//The specific logic of each topic
}

Core idea: optimize the simple algorithm to O(n)

Question 1: there is a string like abc def hij. Please output each word (without spaces) and each word occupies one line.

#include <iostream>
#include <string>
using namespace std;

int main(){
    string str;
    getline(cin,str);
    //cout<<str<<endl;
    int n=str.size();
    for(int i=0;i<n;i++){
        int j=i;
        while(j<n && str[j]!=' ') j++;
        for(int k=i;k<j;k++) cout<<str[k];
        cout<<endl;
        i=j;
    }
    return 0;
}

Input:
abc def ghi
===============
Output:
abc
def
ghi

AcWing 799. Longest continuous unrepeated subsequence

We specify that pointer i is the end point and pointer j is the starting point. Enumerate the end point first and then the starting point.

//Violent practices O(n^2)
for(int i=0;i<n;i++){
	for(int j=0;j<=i;j++){
		if(check(j,i)){
			res=max(res,i-j+1);
		}
	}
}

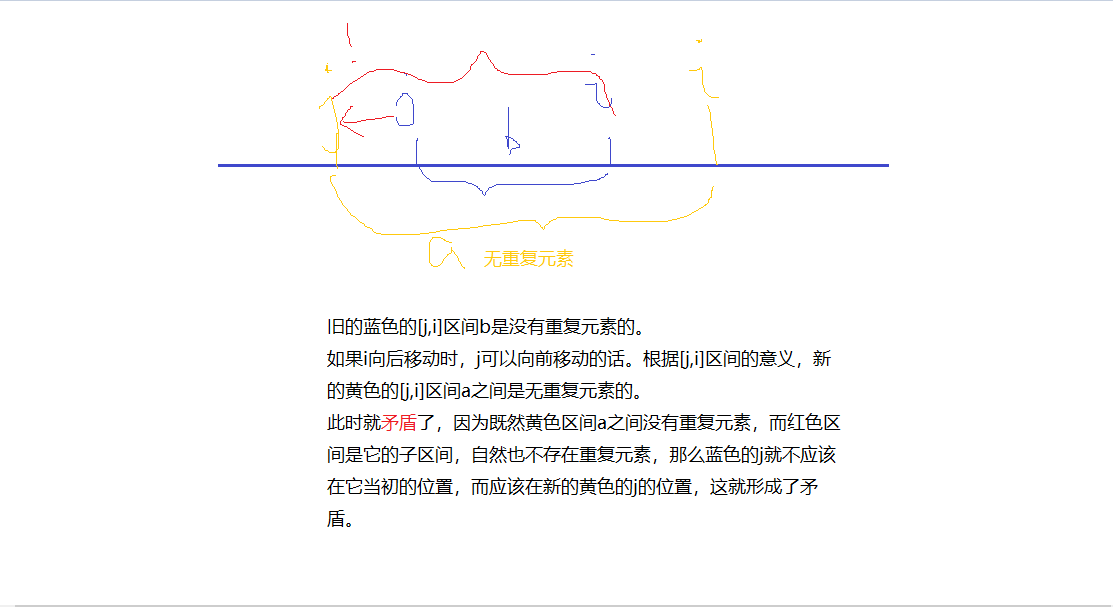
The meaning of pointer j: where is the farthest left of j

Optimization ideas:

The idea of enumerating the end points i is the same as the naive algorithm. Let's see where the left end point of the interval with each i as the right end point is farthest from it.

We move the end point i one position at a time, and then find out where the new leftmost j can be.

When the end point moves backward, j will not go forward, which is monotonous. All can optimize simple practices.

//Double pointer algorithm: O(n)
for(int i=0;i<n;i++){
	//check to see if there are duplicate elements between J and I
	//As long as there is a repeating element between j and i, move j back one bit until there is no repeating element between j and i
	while(j<=i && check(j,i)) j++;
	res=max(res,i-j+1);
}

#include <iostream>
using namespace std;
const int N=100010;
int n;
int a[N];
//s stores the number of occurrences of each number in the current interval from j to i
int s[N];

int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    int res=0;
    for(int i=0,j=0;i<n;i++){
        //Add new number each time a[i]
        s[a[i]]++;
        //So if there are repeated numbers, it must be a[i] repeated
        while(s[a[i]]>1){
            s[a[j]]--;
            j++;
        }
        res=max(res,i-j+1);
    }
    cout<<res<<endl;
    return 0;
}

Bit operation

Application 1: find the k-th bit in the binary representation of n

n=15= ( 1111 ) 2 (1111)_2 (1111)2​

First shift the k to the last position n > > k

Let's take a look at the number of bits x&1

So the formula is: n > > k-1

Application 2: lowbit(x) returns the last bit 1 of X

x= ( 1010 ) 2 (1010)_2 (1010)2​

lowbit(x)= ( 10 ) 2 (10)_2 (10)2​

x= ( 101000 ) 2 (101000)_2 (101000)2​

lowbit(x)= ( 1000 ) 2 (1000)_2 (1000)2​

Formula: X & - x

-X is the complement, which is the inverse of the original code plus one, that is - x=~x+1

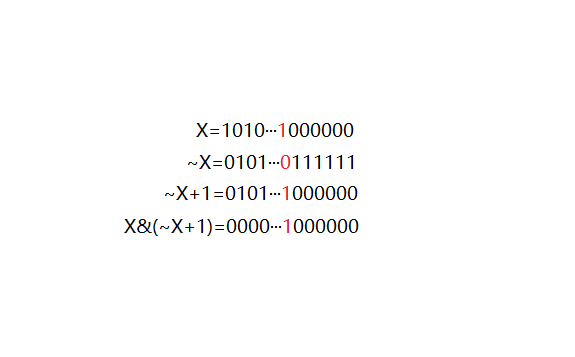
Common applications: subtract the last 1 every time and count the number of 1 in binary number x

AcWing 801. Number of 1 in binary

#include <iostream>
using namespace std;
int n;

int lowbit(int x){
    return x&-x;
}

int main(){
    scanf("%d",&n);
    while(n--){
        int x;
        scanf("%d",&x);
        int cnt=0;
        while(x!=0){
            x-=lowbit(x);//Subtract the last 1 of x each time
            cnt++;
        }
        cout<<cnt<<" ";
    }
    return 0;
}

Discretization

(this refers specifically to the ordered discretization of integers)

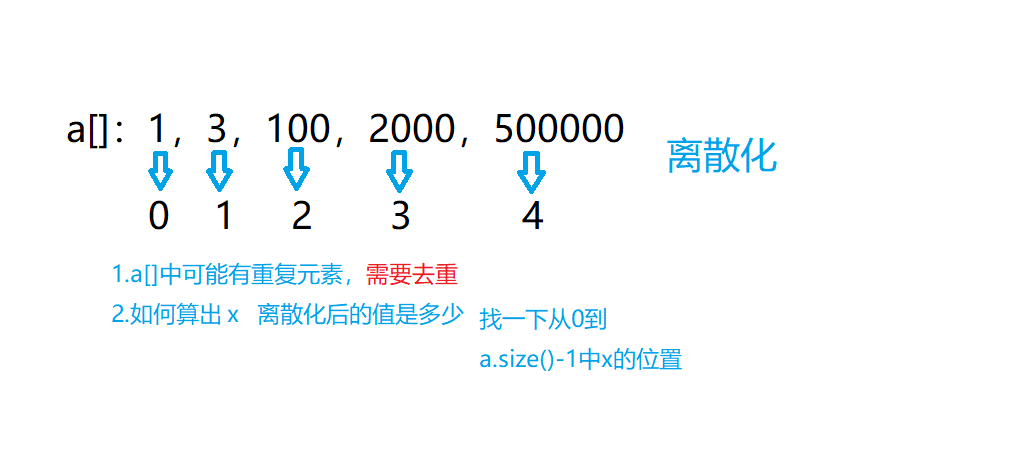
We have some values now, and their range is [0,10^9], but the number of these numbers is relatively small, and the number is between [0,10^5]

The characteristics of these values are: the range of values is large, but the number is small and sparse

In some cases, we may need to use these values as subscripts to solve the problem. It is very unrealistic to open an array without processing.

Therefore, we need to map this numerical sequence to natural numbers starting from 0 or 1

How to find out the value of a number x after discretization? Let's analyze it.

We use the subscript of this number as its discretized value, so the binary search can find the subscript of number x in all.

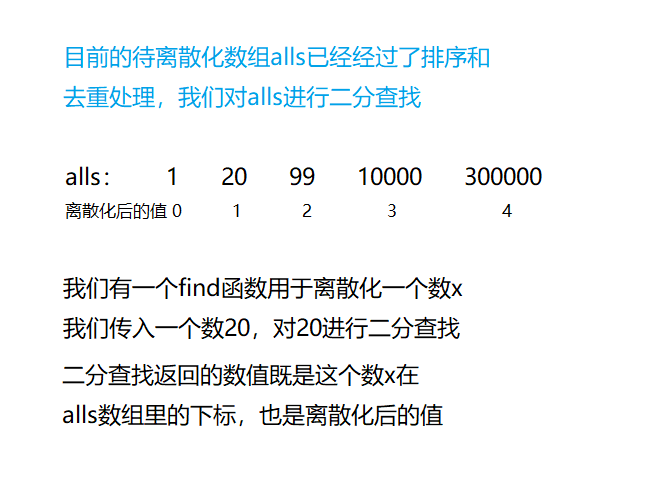
AcWing 802. Interval and

thinking

Put all the subscript in alls, sort it out, and then call the find function to map it to the natural number from 1.

Adding c to the integer x is: first find the value k of X after discretization, and then a[k]+=c on the discretized sequence

When finding the sum of all numbers between [l,r], first discretize L and r to the corresponding subscript position K l K_l Kl​ K r K_r Kr, please a again[ K l K_l Kl] to a[ K r K_r The sum of all numbers between Kr] is OK (use prefix and)

Usage of pair Summary of basic usage of C++ pair (sorting)
A big man gave this inscription a super detailed explanation AcWing 802. Interval and

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

//Store x and c and l and r with pair
typedef pair<int,int> PII;
const int N=300010;
int n,m;
//a[N] is the discretized array, and s[N] is the prefix and array
int a[N],s[N];
//All is a container for the number to be discretized
vector<int> alls;
//add stores x and C, and query stores l and r
vector<PII> add,query;

//The find function is used to discretize a number
int find(int x){
    int l=0,r=alls.size()-1;
    //Use dichotomy
    while(l<r){
        int mid=(l+r)>>1;
        if(alls[mid]>=x) r=mid;
        else l=mid+1;
    }
    return r+1;
}

int main(){
    scanf("%d%d",&n,&m);
    //Preparation operation: read data into and put them into corresponding containers respectively
    while(n--){
        int x,c;
        scanf("%d%d",&x,&c);
        add.push_back({x,c});
        alls.push_back(x);
    }
    while(m--){
        int l,r;
        scanf("%d%d",&l,&r);
        query.push_back({l,r});
        alls.push_back(l);
        alls.push_back(r);
    }
    //Sort and de duplicate all
    sort(alls.begin(),alls.end());
    alls.erase(unique(alls.begin(),alls.end()), alls.end());
    //At this time, although the data in the all container is de duplicated, it is still not discretized
    //The following is the add operation
    for(auto item:add){
        //Call the find function to discretize item.first, that is, x in the topic
        int t=find(item.first);
        a[t]+=item.second;
    }
    //The prefix sum [all. Size() is calculated because after discretization, the range is reduced and the number does not change]
    for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i];
    //The following is the query operation
    for(auto item:query){
        int l=find(item.first),r=find(item.second);
        cout<<s[r]-s[l-1]<<endl;
    }
    return 0;
}

Make your own wheels and implement a unique function

#include <iostream>
#include <vector>
using namespace std;

int unique(vector<int> &a){
    int j=0;
    for(int i=0;i<a.size();i++){
        if(i==0 || a[i]!=a[i-1]) a[j++]=a[i];
    }
    //a[0] to a[j-1] are the numbers that are not repeated in all a
    return j-1;
}

int main(){
    vector<int> a={1,2,2,2,3,3,3,3,3,4,4,5,6,6,7};
    cout<<unique(a)<<endl;
    return 0;
}
//The result is 6

Interval merging

There are many intervals. If two intervals intersect, they are merged into the same interval

Green is the merged interval

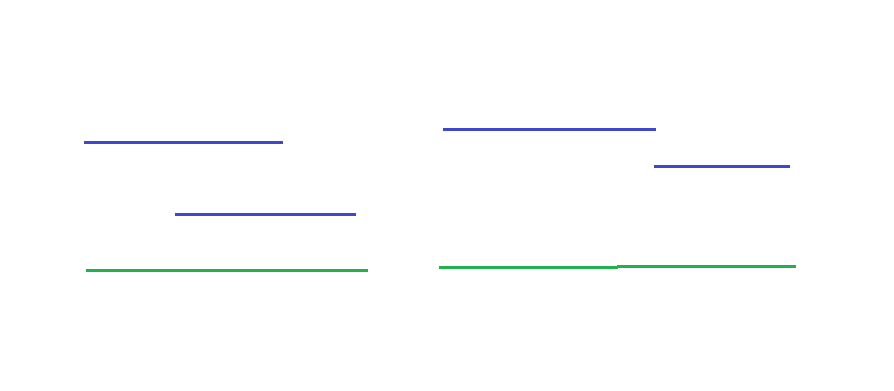
Idea:

First, sort all intervals according to the sorting rules of the left endpoint

Then maintain an interval A. there may be three relationships between interval b and interval a after interval a

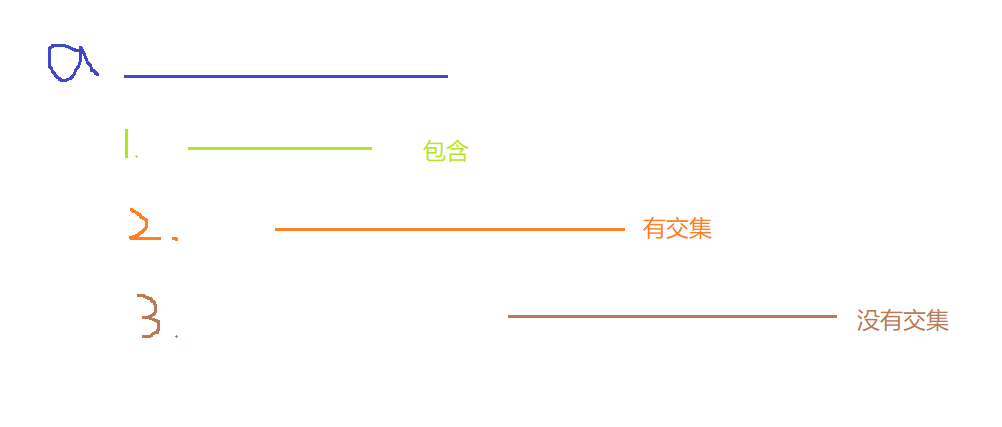
Interval b cannot be in front of interval a, that is, the left end point of interval b must be less than or equal to the left end point of interval a, because we have sorted according to the sorting rules of the left end points.

When the case is 1 (inclusive), the interval maintained by us remains unchanged and no operation is required; In case 2 (with intersection), we extend interval A. in case 3 (without intersection), we can put interval a into the answer and update the interval to b

When interval b and interval a do not intersect, it means that interval b and all intervals behind interval b do not intersect with interval a, so we update the maintained interval to interval b

AcWing 803. Interval merging

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

typedef pair<int,int> PII;
int n;
vector<PII> segs;

bool cmp(PII a,PII b){
    if(a.first!=b.first) return a.first<b.first;
    else return a.second<b.second;
}

void merge(vector<PII> &segs){
    vector<PII> res;
    sort(segs.begin(),segs.end(),cmp);
    //We set the first maintenance interval from negative infinity to negative infinity
    int st=-2e9,ed=-2e9;
    for(auto seg:segs){
        if(ed<seg.first){
            if(st!=-2e9) res.push_back({st,ed});
            st=seg.first,ed=seg.second;
        }
        else ed=max(ed,seg.second);
    }
    //And add the last interval to the answer
    if(st!=-2e9) res.push_back({st,ed});
    segs=res;
}

int main(){
    scanf("%d",&n);
    while(n--){
        int l,r;
        scanf("%d%d",&l,&r);
        segs.push_back({l,r});
    }
    merge(segs);
    cout<<segs.size()<<endl;
    return 0;
}